31. 1049. 最后一块石头的重量 II, 494.目标和,474.一和零

class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int sum = 0;for(int stone : stones) sum += stone;int bagSize = sum /2;vector<int> dp(bagSize + 1, 0);for(int i = 0; i < stones.size(); i++){ //遍历物品for(int j = bagSize; j >= stones[i]; j--){ //遍历背包dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);}}return sum - 2*dp[bagSize];}
};
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int ans = 0, sum = 0;for(int num : nums) sum += num;if((sum - target) % 2 != 0 || abs(sum) < abs(target)) return 0;int bagSize = (sum - target)/2;// dp[j] 表示:填满j(包括j)这么大容积的包,有dp[j]种方法vector<int> dp(bagSize + 1, 0);dp[0] = 1;for(int i = 0; i < nums.size(); i++){for(int j = bagSize; j >= nums[i]; j--){dp[j] += dp[j - nums[i]]; //注意理解递推公式!!!!!!} }return dp[bagSize];}
};
本题中strs 数组里的元素就是物品,每个物品都是一个!而m 和 n相当于是一个背包,两个维度的背包。 注意理解题目中最大子集长度的含义!!!!!!
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {// dp[i][j]:最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0)); //默认初始化0for(string str : strs){ //遍历物品int zeroNum = 0, oneNum= 0;for(char c : str){if(c == '0') zeroNum++;else oneNum++;}for(int i = m; i >= zeroNum; i--){ //遍历背包容量且从后向前遍历!for(int j = n; j >= oneNum; j--){dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);}}}return dp[m][n];}
};
相关文章:

31. 1049. 最后一块石头的重量 II, 494.目标和,474.一和零
class Solution { public:int lastStoneWeightII(vector<int>& stones) {int sum 0;for(int stone : stones) sum stone;int bagSize sum /2;vector<int> dp(bagSize 1, 0);for(int i 0; i < stones.size(); i){ //遍历物品for(int j bagSize; j >…...

PDF 中图表的解析探究
PDF 中图表的解析探究 0. 引言1. 开源方案探究 0. 引言 一直以来,对文档中的图片和表格处理都非常有挑战性。这篇文章记录一下最近工作上在这块的探究。图表分为图片和表格,这篇文章主要记录了对表格的探究。还有,我个人主要做日本项目&…...
)
递推(C语言)
文章目录 1.斐波那契数列2.太波那契数列3.二维递推问题4.实战4.1 力扣509 斐波那契数4.2 力扣70 爬楼梯4.3 力扣119 杨辉三角|| 递推最通俗的理解就是数列,递推和数列的关系就好比 算法 和 数据结构 的关系,数列有点 像数据结构中的线性表(可以是顺序表&…...
安卓微信8.0之后如何利用缓存找回的三天之前不可见的朋友圈图片
安卓微信8.0之后如何利用缓存找回的三天之前不可见的朋友圈图片 复习了下安卓程序的知识,我们会了解到,安卓程序清楚数据的时候有两个选项 一个是清除全部数据一个是清除缓存。 清除全部数据表示清除应用数据缓存。 对于安卓微信8.0之后而言࿰…...
 总结(九))
ES6 Class(类) 总结(九)
ES6 中的 class 是一种面向对象编程的语法糖,提供了一种简洁的方式来定义对象的结构和行为。 JavaScript 语言中,生成实例对象的传统方法是通过构造函数。下面是一个例子。 function Point(x, y) {this.x x;this.y y; } Point.prototype.toString fu…...

使用 Vue.js 和 Element Plus 实现自动完成搜索功能
使用 Vue.js 和 Element Plus 实现自动完成搜索功能 一、前言1.环境准备2.组件配置3.后端数据请求4.样式5.总结 一、前言 在前端开发中,实现自动完成(autocomplete)功能可以极大地提升用户体验,特别是在需要用户输入和选择内容的…...

SpringBoot自定义starter
SpringBoot自定义starter 1、SpringBoot之starter机制 1.1、什么是自定义starter SpringBoot中的starter是一种非常重要的机制(自动化配置),能够抛弃以前繁杂的配置,将其统一集成进starter,应用者只需要在maven中引入starter依赖&#…...

深入探索大语言模型
深入探索大语言模型 引言 大语言模型(LLM)是现代人工智能领域中最为重要的突破之一。这些模型在自然语言处理(NLP)任务中展示了惊人的能力,从文本生成到问答系统,无所不包。本文将从多个角度全面介绍大语…...
)
querylist多线程采集curlMulti时,报错Curl error(60)
前言 在使用querylist多线程采集的时候,报错: Curl error(60)。测试了下用http时没有问题,https时有问题。其原因在于多线程采集库引用的另一个库有问题。需要手动更改。 解决 找到:vendor/ares333/php-curl/src/Curl.php 文件,…...

Python数据分析~~美食排行榜
目录 1.模块的导入和路径的选择 2.访问前面五行数据 3.按照条件进行筛选 4.获取店铺评分里面的最高分 5.打印对应的店铺的名字 1.模块的导入和路径的选择 # 导入pandas模块,简称为pd import pandas as pd # 使用read_csv()函数 # TODO 读取路径"/Users/fe…...

Linux下解压.tar.gz文件
.tar.gz 是一种常用的压缩包格式,尤其在Unix、Linux以及macOS系统中非常普遍。这个格式结合了两种不同的功能: Tar (.tar): “Tar” 是“Tape Archive”的缩写,最初是为了将数据备份到磁带上而设计的。Tar命令可以将多个文件和目录打包成一个…...

【电商选品干货】差异化卖点要这样打造,80%商家却做不到
今天就给大家说说,如何去挖掘产品的差异化卖点?我们要找差异化卖点,就是因为我们的产品转化率不足,通常有下面几点原因: 1、产品差异化卖点不足,商家占比30% 2、流量和产品卖点不匹配,商家占比…...

LabVIEW比例压力控制阀自动测试系统
开发了一套基于LabVIEW编程和PLC控制的比例控制阀自动测试系统。该系统能够实现共轨管稳定的超高压供给,自动完成比例压力控制阀的耐久测试、流量滞环测试及压力-流量测试。该系统操作简便,具有高精度和高可靠性,完全满足企业对自动化测试的需…...

运营商认证API在Java、Python、PHP中的使用教程
随着数字化浪潮的推进,实名认证已深入我们生活的方方面面,从线上购物到电子资金转移,手机号已成为注册账号的主要凭证。然而,这也带来了身份验证的难题和手机号被盗用注册账号的风险。在信息爆炸的时代背景下,确保每个…...

用虚拟机,可以在x86的电脑上虚拟出arm的电脑吗
1.用虚拟机,可以在x86的电脑上虚拟出arm的电脑吗 是的,可以在x86的电脑上使用虚拟机技术虚拟出ARM架构的电脑。以下是通过虚拟机实现x86电脑上虚拟ARM电脑的几个关键步骤: 选择合适的虚拟化软件:通常,你可以使用如QE…...

富格林:可信观念摆脱暗箱陷阱
富格林指出,投资者产生的暗箱亏损多半是由于被不可信观念的迷惑影响,以为真的可以毫不费力就能赚钱,最后发现连交易的本金都打水漂了。事实上,投资市场并不像大家想得那么简单。要想安全实现交易成功,避免暗箱陷阱&…...
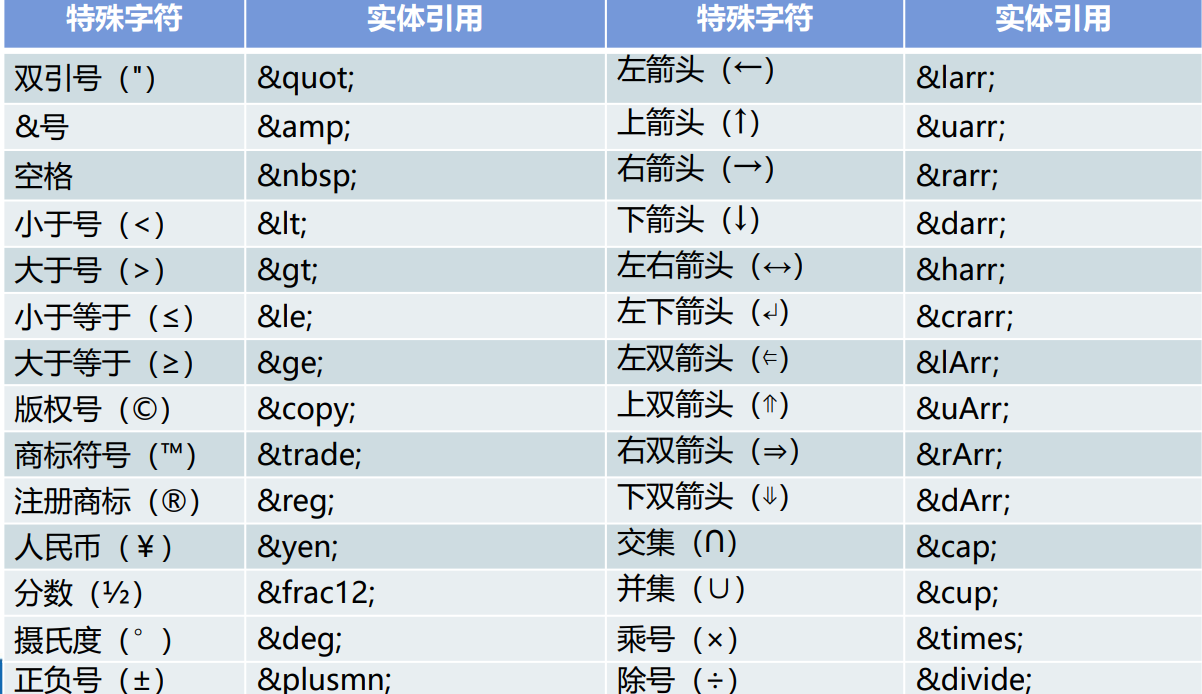
WEB前端01-HTML5基础(01)
一.WEB相关概念 软件架构 C/S: Client/Server (客户端/服务器端):在用户本地有一个客户端程序,在远程有一个服务器端程序 优点:用户体验好 缺点:开发、安装,部署,维护麻烦 B/S: Br…...

JUC-常见方法与线程的状态
常见方法 start()与run() 主线程直接调用某个线程t1的run()方法,run方法也会执行,但是并不会启动新的线程,而是有主线程调用的run方法,必须使用start才能启动新线程,但是start只能调用一次。 sleep()与yield() sle…...

如果你酿的酒是黄色,说明肯定是 “糊锅”了。
刚刚酿出的酒一般都是清澈见底的,如果你酿的酒是黄色,说明肯定是 “糊锅”了。这样的酒不仅颜色是黄的,而且还能闻到一股特别浓厚的 焦糊味。 这样的酒,米酒小哥是非常非常熟悉的,因为刚开始学习酿酒的那段时 间&#…...

国漫推荐07
玄幻、奇幻 1.侠岚系列 《侠岚》(第1至6季) 《画江湖之侠岚》(侠岚第7季) 2.《斗破苍穹》 三十年河东,三十年河西,莫欺少年穷! 3.《武动乾坤》(第1至4季) 4.《妖神记》…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
