二进制,八进制,十进制,十六进制的相互转换【简单易懂】(含代码模板)
目录
二进制转十进制
十进制原理:
二进制转十进制计算:
八、十六进制转十进制
八、十六进制转十进制计算:
十进制转其他进制
十进制转二进制:
十进制转八进制:
十进制转十六进制:
不同进制之间的相互转换
练一练手:
二进制转十进制

十进制原理:
为了方便学习二进制,我们先来看一下十进制的原理,十进制的特点就是有10个符号来表示一个数字,分别是0123456789;就比如这个数字235,他的个位是5,代表5个1 ,十位是3,代表3个10,百位是2,代表两个100,这个数字就代表这三个值的和。换一种方式来表示,他就是5×10^0加上3×10^1加上2×10^2也就是200+30+5,最后得出了235;
二进制其实也是一样的原理,再十进制中有10个可用的符号来表示一个数字,在二进制中呢,就只用两个可用的符号来表示一个数字,分别是0和1。在十进制中,我们可以把0-9种不同的符号放到不同的位中,组成各种各样的数字,在二进制中,我们把0和1两种不同的符号,放入不同的位中,同样可以组成各种各样的数字。
二进制转十进制计算:
如数字1011,我把这个二进制数字放在这个十进制数字的边上,这样我们就可以模仿刚才我们算十进制的方法,把这个二进制数字算出来。在我们刚才算十进制的过程中,从右边数第一位需要乘以2的零次方、第二位乘2的一次方……(如图),将所以乘数相加就是十进制表示
八、十六进制转十进制

我们现在知道了⒉进制怎么转成10进制,八进制和十六进制又是怎么回事儿呢。其实都是一样的原理,十进制有十个符号表示一个数字,二进制有两个符号表示一个数字,八进制有8个符号用来表示一个数字。分别是01234567,十六进制有16个符号来表示一个数字分别是0123456789ABCDEF。
八、十六进制转十进制计算:
八进制的0到7就对应十进制的0到7,十六进制的0到F就对应十进制的0到15。(如上图)
我们来看一个八进制的数字,227,我们还是用和刚才同样的方法来计算,从右边数第一位的7乘以8的0次方,第二位7乘以8的1次方,第三位的7乘以8的2次方,也就是2×64 + 7×8 +7×1,最后得出128+56+7=191,也就是8进制中的二二七等于十进制中的一九一;
十六进制同理可得,只需要把ABCDEF转化成对应的十进制即可;
十进制转其他进制
我们现在知道了每个进制怎么转换成十进制,那么,十进制的数字怎么转换成其他进制呢?一个普遍的方法就是连除法
十进制转二进制:

对于这个十进制数字29来说,如果要转换成二进制,我们就把他先除以2,得到14余1、再把14除以二,得到7余0,再把7除以二,得到3余1,再把3除以二,得到1余1,再把1除以二,得到0余1,一直除到到这个商等于0,就可以结束了,最后把得出来的最右边的这一列余数从下往上反向排列,就可以得出一个二进制数11101,我们就成功的把这个十进制数字29转换成了二进制数字11101
十进制转八进制:

我们同样可以用连除法把十进制数字转换成8进制, 比如说这个十进制数字900,我们把它先除以8得到112余4,再把112除以8得到14余0,再把14除以8得到1余6,再把1除以8得到0余1,直到商等于0,就可以结束了,最后把得出来的最右边的这一列余数从下往上反向排列,就可以得出一个二进制数1604
十进制转十六进制:

与上文同理,字母转换即可
不同进制之间的相互转换

拿二进制转八进制举例,由于2的三次方为8, 所以每3位可以转换为1位八进制; 如二进制10 111 001前面的001等于1*2^0+0*2^1+0*2^2,和为八进制的1,以此类推得2 7 1,那么二进制10111001转化为八进制就是271(十六进制同理)
笔记篇,素材来源于up主“我是2045” ;
练一练手:
P1143 进制转换

#include<bits/stdc++.h>
using namespace std;
string s;
int a,b;
int wei,sum,num;
int c[10000010];
int main()
{cin>>a>>s>>b;for(int i=0;i<s.size();i++){if(s[i]<'A'){wei=pow(a,s.size()-1-i); //从大向小取位wei*=(s[i]-'0');sum+=wei;}else{wei=pow(a,s.size()-1-i);wei*=(s[i]-'A'+10);sum+=wei;}}//sum为a进制转化为十进制的值while(sum>0){c[num++]=sum%b; //连除法sum/=b;}for(int i=num-1;i>=0;i--) //对应前面,“从下到上输出”{if(c[i]>=10) printf("%c",c[i]+'A'-10); //可能是字符,cout默认数字else cout<<c[i];}return 0;
}

相关文章:

二进制,八进制,十进制,十六进制的相互转换【简单易懂】(含代码模板)
目录 二进制转十进制 十进制原理: 二进制转十进制计算: 八、十六进制转十进制 八、十六进制转十进制计算: 十进制转其他进制 十进制转二进制: 十进制转八进制: 十进制转十六进制: 不同进制之间的相互转…...
Redis技术详解
Redis技术详解 Redis是一种支持key-value等多种数据结构的存储系统。可用于缓存,事件发布或订阅,高速队列等场景。支持网络,提供字符串,哈希,列表,队列,集合结构直接存取,基于内存&…...
解决mybatis-plus updateById方法不能set null
原因 因为 MyBatis-Plus 自带的更新方法,都有对对象空值进行判空。只有不为空的字段才会进行数据更新 所以像updateById等方法,在更新时会自动忽略为null的字段,只更新非null字段值 但在某些情况下,我们的需求就是将数据库中的值…...

Linux的mysql 数据库及开发包安装
注意:以下操作都以 root 用户进行操作 直接按照下列步骤在命令行输入即可 下载 1: sudo yum install -y mariadb 2: sudo yum install -y mariadb-server 3: sudo yum install -y mariadb-devel 接下来配置文件:在相应…...

π-Day快乐:Python可视化π
π-Day快乐:Python可视化π 今天是3.14,正好是圆周率 π\piπ 的前3位,因此数学界将这一天定为π\bold{\pi}π day。 π\piπ 可能是最著名的无理数了,人类对 π\piπ 的研究从未停止。目前人类借助计算机已经计算到 π\piπ 小数…...
【论文速递】ACM MM 2022 - 基于统一对比学习框架的新闻多媒体事件抽取
【论文速递】ACM MM 2022 - 基于统一对比学习框架的新闻多媒体事件抽取 【论文原文】:Multimedia Event Extraction From News With a Unified Contrastive Learning Framework 【作者信息】:Liu, Jian and Chen, Yufeng and Xu, Jinan 论文ÿ…...

数据库分库分表
一、为什么要分库分表 如果一个网站业务快速发展,那这个网站流量也会增加,数据的压力也会随之而来,比如电商系统来说双十一大促对订单数据压力很大,Tps十几万并发量,如果传统的架构(一主多从),主库容量肯定无法满足这么高的Tps,业务越来越大,单表数据超出了数据库支持…...

【C缺陷与陷阱】----语义“陷阱”
💯💯💯 本篇处理的是有关语义误解的问题:即程序员的本意是希望表示某种事物,而实际表示的却是另外一种事物。在本篇我们假定程序员对词法细节和语法细节的理解没有问题,因此着重讨论语义细节。导言…...

JavaWeb--VUE
VUE1 概述2 快速入门3 Vue 指令3.1 v-bind & v-model 指令3.2 v-on 指令3.3 条件判断指令3.4 v-for 指令4 生命周期5 案例5.1 需求5.2 查询所有功能5.3 添加功能目标 能够使用VUE中常用指令和插值表达式能够使用VUE生命周期函数 mounted 1 概述 接下来我们学习一款前端的框…...

2分钟彻底搞懂“高内聚,低耦合”
💗推荐阅读文章💗 🌸JavaSE系列🌸👉1️⃣《JavaSE系列教程》🌺MySQL系列🌺👉2️⃣《MySQL系列教程》🍀JavaWeb系列🍀👉3️⃣《JavaWeb系列教程》…...

网络编程UDP TCP
定义:关注底层数据的传输 区分网页编程:关注上层应用 端口号:区分软件 2个字节 0~65535表示端口号 同一协议下端口号不能冲突 8000以下称为预留端口号,建议之间设置端口号为8000以上 常见的端口号: 80:http 8080:tomcat 3306:mysql 1521:oracle InetSocketAddress:此类实现IP套…...
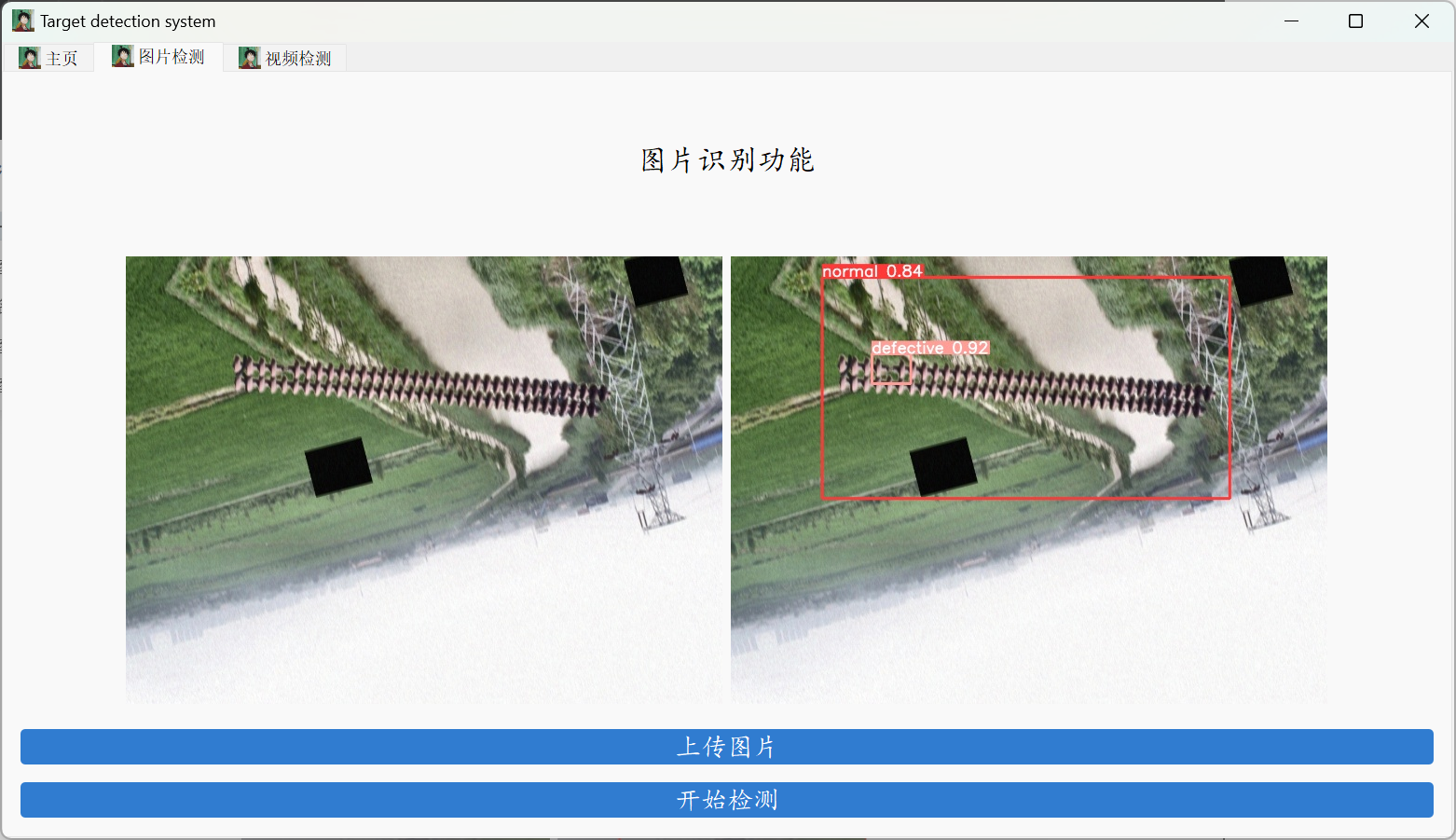
【2023-Pytorch-检测教程】手把手教你使用YOLOV5做电线绝缘子缺陷检测
随着社会和经济的持续发展,电力系统的投资与建设也日益加速。在电力系统中,输电线路作为电能传输的载体,是最为关键的环节之一。而绝缘子作为输电环节中的重要设备,在支撑固定导线,保障绝缘距离的方面有着重要作用。大…...
)
交叉编译(NDK)
文章目录前言Android-NDK使用NDK目录结构主流的Android NDK交叉编译前言 交叉编译是指在一种计算机体系结构上编译和构建应用程序,但是生成的可执行文件和库是针对另一种不同的体系结构,比如ARM、MIPS、PowerPC、x86 等。 常见的交叉编译工具集&#x…...

【数据库】MySQL 解读事务的意义及原则
目录 1.事务的概念 2.为什么要用事物 3.使用 4.事务的原则(ACID) 4.1原子性(Atomicity) 4.2一致性(Consistency) 4.3持久性(Durability) 4.4隔离性(Isolation…...
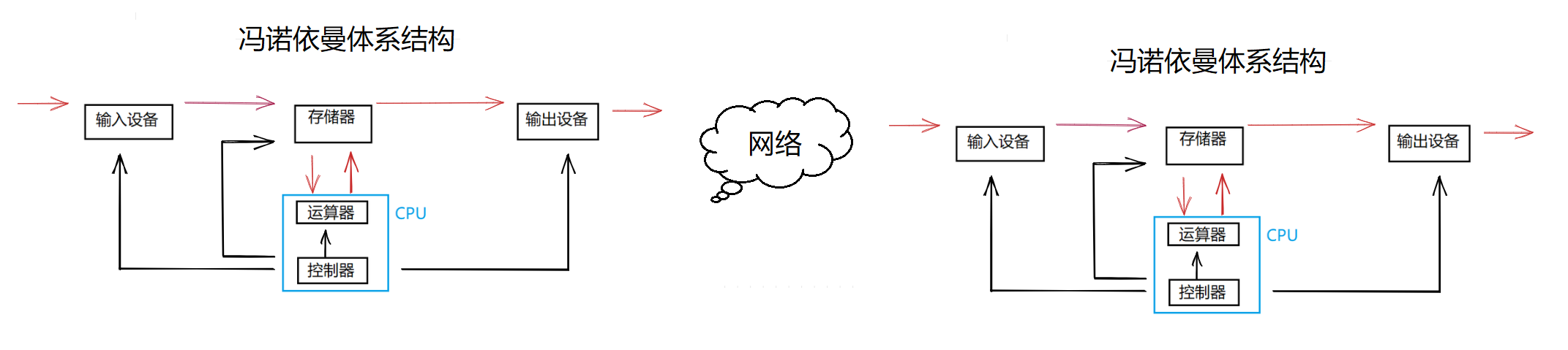
【Linux】冯诺依曼体系结构
冯诺依曼体系结构一、计算机结构体系来源二、冯诺依曼体系结构三、冯诺依曼体系结构中的数据流动一、计算机结构体系来源 研制电子计算机的想法产生于第二次世界大战期间,主要用来进行弹道计算,在"时间就是胜利"的战争年代,迫切需…...

【小白】git是什么?gitee和git和github的关系?
gitee问题一、git是什么?gitee和git和github的关系?问题二、能不能通俗易懂的说?问题一、git是什么?gitee和git和github的关系? Git是一种版本控制系统,用于管理文件的版本、记录文件的修改历史以及协同开…...

UDS 14229 -1 刷写34,36,37服务,标准加Trace讲解,没理由搞不明白
🍅 我是蚂蚁小兵,专注于车载诊断领域,尤其擅长于对CANoe工具的使用🍅 寻找组织 ,答疑解惑,摸鱼聊天,博客源码,点击加入👉【相亲相爱一家人】🍅 玩转CANoe&…...

【Android -- 软技能】聊聊程序员的软技能
什么是软技能? 所谓软技能,就是相对于「硬技能」而言的技能,对于程序员来说,「硬技能」就是计算机专业技术能力,软技能则是专业之外的所有技能,包括职业规划能力、处理人际关系能力、专业态度、做事的方式…...

【Java学习笔记】27.Java 抽象类
Java 抽象类 在面向对象的概念中,所有的对象都是通过类来描绘的,但是反过来,并不是所有的类都是用来描绘对象的,如果一个类中没有包含足够的信息来描绘一个具体的对象,这样的类就是抽象类。 抽象类除了不能实例化对象…...

Vite4 + Vue3 + vue-router4 动态路由
动态路由,基本上每一个项目都能接触到这个东西,通俗一点就是我们的菜单是根据后端接口返回的数据进行动态生成的。表面上是对菜单的一个展现处理,其实内部就是对router的一个数据处理。这样就可以根据角色权限或者一些业务上的需求࿰…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
