xlwings 链接到 指定sheet 从别的 excel 复制 sheet 到指定 sheet
重点
可以参考 宏录制
cell = sheet.range('G4')cell.api.Hyperlinks.Add(Anchor=cell.api, Address="", SubAddress="'001-000-023+01'!A1")
def deal_excel(self):with xw.App(visible=True) as app:wb = app.books.open(self.summary_path, update_links=False)sheet = wb.sheets[0]for pn in self.pn_list:pn_path = os.path.join(cuixiao_data_raw, f'{pn}.xlsx')wb_pn = app.books.open(pn_path, update_links=False)sheet_pn = wb_pn.sheets[0]new_sheet = sheet_pn.copy(after=wb.sheets[0])new_sheet.name = pnfor i in range(4, 99999):if sheet.range(f'G{i}').value:cell = sheet.range(f'G{i}')value = cell.valueprint('value', i, value)cell.api.Hyperlinks.Add(Anchor=cell.api, Address="", SubAddress=f"'{value}'!A1")else:break# cell = sheet.range('G4')# cell.api.Hyperlinks.Add(Anchor=cell.api, Address="", SubAddress="'001-000-023+01'!A1")sheet.name = 'Summary'sheet.range('A1').value = ''sheet.activate() # 激活指定的工作表sheet.range('A1').select() # 选择特定的单元格result_path = os.path.join(cuixiao_data_result, f'{today}_result.xlsx')wb.save(result_path)参考
https://blog.csdn.net/xcntime/article/details/115640772
相关文章:

xlwings 链接到 指定sheet 从别的 excel 复制 sheet 到指定 sheet
重点 可以参考 宏录制 cell sheet.range(G4)cell.api.Hyperlinks.Add(Anchorcell.api, Address"", SubAddress"001-000-02301!A1")def deal_excel(self):with xw.App(visibleTrue) as app:wb app.books.open(self.summary_path, update_linksFalse)sheet…...

风光摄影:相机设置和镜头选择
写在前面 博文内容为《斯科特凯尔比的风光摄影手册》读书笔记整理涉及在风景拍摄中一些相机设置,镜头选择的建议对小白来讲很实用,避免拍摄一些过曝或者过暗的风景照片理解不足小伙伴帮忙指正 😃,生活加油 99%的焦虑都来自于虚度时间和没有好…...
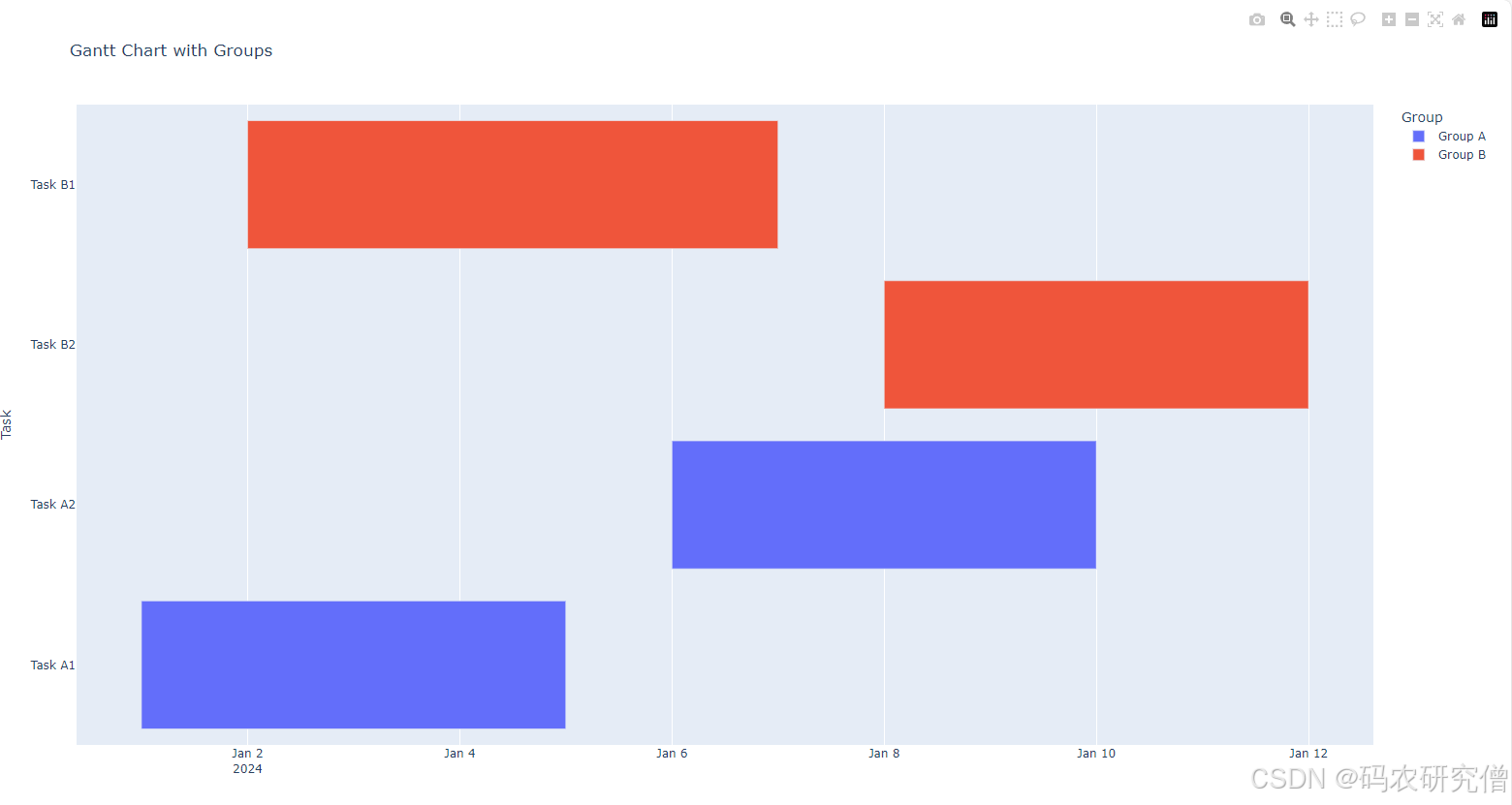
python制作甘特图的基本知识(附Demo)
目录 前言1. matplotlib2. plotly 前言 甘特图是一种常见的项目管理工具,用于表示项目任务的时间进度 直观地看到项目的各个任务在时间上的分布和进度 常用的绘制甘特图的工具是 matplotlib 和 plotly 主要以Demo的形式展示 1. matplotlib 功能强大的绘图库&a…...

javascript设计模式总结
参考 通过设计模式可以增加代码的可重用性、可扩展性、可维护性 设计模式五大设计原则 单一职责:一个程序只需要做好一件事,如果结构过于复杂就拆分开,保证每个部分独立 开放封闭原则:对扩展开放,对修改封闭。增加需…...

gpt-4o看图说话-根据图片回答问题
问题:中国的人口老龄化究竟有多严重? 代码下实现如下:(直接调用openai的chat接口) import os import base64 import requests def encode_image(image_path): """ 对图片文件进行 Base64 编码 输入…...

【MySQL】7.MySQL 的内置函数
MySQL的内置函数 一.日期函数二.字符串函数三.数学函数四.其它函数 一.日期函数 函数名称说明current_date()当前日期current_time()当前时间current_timestamp当前时间戳(日期时间)date(datetime)截取 datetime 的日期部分date_add(date, interval d_value_type)给 date 添加…...

爬虫:Sentry-Span参数逆向
在抓某眼查数据太过频繁时会出现极验的验证码。极验的教程有很多,主要是发现在这里获取验证码的时候需要携带参数Sentry-Span。在这里记录一下逆向的主要过程,直接上补环境的代码。 window global; location {}; my_log console.log;(function () {l…...
——FFmpeg源码中通过SPS属性计算视频分辨率的实现)
音视频入门基础:H.264专题(12)——FFmpeg源码中通过SPS属性计算视频分辨率的实现
一、引言 在上一节《音视频入门基础:H.264专题(11)——计算视频分辨率的公式》中,讲述了通过SPS中的属性计算H.264编码的视频的分辨率的公式。本文讲解FFmpeg源码中计算视频分辨率的实现。 二、FFmpeg源码中计算视频分辨率的实现…...

基于颜色模型和边缘检测的火焰识别FPGA实现,包含testbench和matlab验证程序
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 (完整程序运行后无水印) 将FPGA仿真结果导入到matlab显示结果: 测试样本1 测试样本2 测试样本3 2.算法运行软件版本 vivado2019.2 …...

golang json反序列化科学计数法的坑
问题背景 func CheckSign(c *gin.Context, signKey string, singExpire int) (string, error) {r : c.Requestvar formParams map[string]interface{}if c.Request.Body ! nil {bodyBytes, _ : io.ReadAll(c.Request.Body)defer c.Request.Body.Close()if len(bodyBytes) >…...

罗技K380无线键盘及鼠标:智慧互联,一触即通
目录 1. 背景2. K380无线键盘连接电脑2.1 键盘准备工作2.2 电脑配置键盘的连接 3. 无线鼠标的连接3.1 鼠标准备工作3.2 电脑配置鼠标的连接 1. 背景 有一阵子经常使用 ipad,但是对于我这个习惯于键盘打字的人来说,慢慢在 ipad 上打字,实在是…...
卸载wps office的几种方法收录
第一种方法: 1.打开【任务管理器】,找到相关程序,点击【结束任务】。任务管理器可以通过左下角搜索找到。 2.点击【开始】-【设置】-【应用】-下拉找到WPS应用,右键卸载,不保留软件配置 …...

SpringCloud第一篇Docker基础
文章目录 一、常见命令二、数据卷三、数据挂载四、自定义镜像五、网络 一、常见命令 Docker最常见的命令就是操作镜像、容器的命令,详见官方文档: https://docs.docker.com/ 需求: 在DockerHub中搜索Nginx镜像,查看镜像的名称 …...

从零开始学习PX4源码3(如何上传官网源码到自己的仓库中)
目录 文章目录 目录摘要1.将PX4源码上传至腾讯工蜂2.从腾讯工蜂克隆源码到本地ubuntu3.如何查看自己源码的版本信息 摘要 本节主要记录从零开始学习PX4源码3(如何上传官网源码到自己的仓库中)及如何查看PX4的固件版本信息,欢迎批评指正! PX4源码版本V1.…...

Docker Compose 启动容器例子
Docker Compose 启动容器例子 Docker Compose 文件 (docker-compose.yml) version: 3.8services:web:image: nginx:latestports:- "8080:80"volumes:- ./html:/usr/share/nginx/htmlnetworks:- webnetdb:image: mysql:latestenvironment:MYSQL_ROOT_PASSWORD: exam…...

守护服务之门:Eureka中分布式认证与授权的实现策略
守护服务之门:Eureka中分布式认证与授权的实现策略 引言 在微服务架构中,服务间的通信安全至关重要。Eureka作为Netflix开源的服务发现框架,虽然本身提供了服务注册与发现的功能,但并不直接提供认证与授权机制。为了实现服务的分…...

核密度估计KDE和概率密度函数PDF(深入浅出)
目录 1. 和密度估计(KDE)核密度估计的基本原理核密度估计的公式核密度估计的应用Python中的KDE实现示例代码 结果解释解释结果 总结 2. 概率密度函数(PDF)概率密度函数(PDF)是怎么工作的:用图画…...

免开steam 脱离steam 进行游戏的小工具
链接:https://pan.baidu.com/s/1k2C8b4jEqKIGLtLZp8YCgA?pwd6666 提取码:6666 我们只需选择游戏根目录 然后输入AppID 点击底部按钮 进行就可以了 关于AppID在:...

深度学习--系统配置流程
Win10系统配置双系统Ubuntu18.04 深度学习台式服务器自装练手1.win10磁盘管理2.下载系统镜像制作U盘3.系统安装4. 安装后的系统设置工作5.配置CUDA环境CUDNN安装 深度学习台式服务器自装练手 写在最前 CUDA最高支持11.4 显卡3060 1.win10磁盘管理 首先对原有磁盘进行分区整理…...

把Docker的虚拟磁盘文件移动到别的盘符
今天清理C盘空间,发现一个很大的文件 ext4.vhdx 足有 15G 之多,发现这个是Docker的虚拟磁盘文件,于是在网上找到移到它的办法,使用 PowerShell 执行下面命令 查看Docker状态和版本 wsl -l -v 关闭Docker服务 wsl --shutdown …...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...
