【每日一练】python之sum()求和函数实例讲解
在Python中, sum()是一个内置函数,用于计算可迭代对象(如列表、元组等)中所有元素的总和。如下实例:
"""
收入支出统计小程序
知识点:用户输入获取列表元素添加sum()函数,统计作用
"""
# 定义支出,收入空列表,用来储存数据
zhichu = []
shouru = []# 用于判断和记录月数
i = 1
print(".........支出:")
#求6个月的总支出,所以这里设置循环6次
while i <= 6:inpz = int(input(f"{i}月支出(元):"))zhichu.append(inpz)i += 1
#定义一个zong变量来接收sum()的来的总和
zong = sum(zhichu)
print(f"您这{i - 1}个月的总支出是:{zong}元")
print(".........收入:")
w = 1
#求6个月的总收入,所以这里设置循环6次
while w <= 6:inps = int(input(f"{w}月收入(元):"))shouru.append(inps)w += 1
#定义一个zong变量来接收sum()的来的总和
zong = sum(shouru)
print(f"您这{w - 1}个月的总收入是:{zong}元")运行结果:

在这个例子中,sum()函数接收一个列表作为求和对象,并返回该列表中所有元素的总和。
场景实例:求列表中数字的总和,并加上一个起始值
# 定义一个列表 numlist = [15,10,15,20] #定义一个初始值, ini=100 #用sum()函数求列表总和并赋值给nub变量 nub=sum(numlist) #列表总和加上sum()的起始值,直接打印出结果(也可以直接在sum(列表,初始值)里写值) print(sum(numlist,ini)) #例:print(sum(numlist,100))
运行结果:160
场景实例:求二维列表(矩阵)中所有元素的总和
#定义一个二维矩阵列表 mat=[[1,2],[3,4],[5,6]] #用for遍历嵌每个套列表元素值并返回给内部sum()计算,然后再传外面sum再计算 print(sum(sum(i)for i in mat ))
场景实例:求字典中所有值的总和
# 定义一个字典,键为字符串,值为数字
data = {'a': 1,'b': 2,'c': 3,'d': 4
}
# 使用 sum() 函数对字典中的所有值求和
total_values = sum(data.values())
# 输出总和
print(total_values) # 输出 10相关文章:

【每日一练】python之sum()求和函数实例讲解
在Python中, sum()是一个内置函数,用于计算可迭代对象(如列表、元组等)中所有元素的总和。如下实例: """ 收入支出统计小程序 知识点:用户输入获取列表元素添加sum()函数,统计作用 "&…...

打造智慧校园德育管理,提升学生操行基础分
智慧校园的德育管理系统内嵌的操行基础分功能,是对学生日常行为规范和道德素养进行量化评估的一个创新实践。该功能通过将抽象的道德品质转化为具体可量化的指标,如遵守纪律、尊师重道、团结协作、爱护环境及参与集体活动的积极性等,为每个学…...

自定义函数---随机数系列函数
大家有没有发现平常在写随机数的时候,需要引入很多的头文件,然后还需要用一些复杂的函数,大家可能不太习惯,于是我就制作了一个头文件 // random_number.h #ifndef RANDOM_NUMBER_H // 预处理指令,防止头文件被重复包含…...
一文了解5G新通话技术演进与业务模型
5G新通话简介 5G新通话,也被称为VoNR,是基于R16及后续协议产生的一种增强型语音通话业务。 它在IMS网络里新增数据通道(Data Channel),承载通话时的文本、图片、涂鸦、菜单等信息。它能在传统话音业务基础上提供更多服…...

视频使用操作说明书-T80002系列视频编码器如何对接海康NVR硬盘录像机,包括T80002系列高清HDMI编码器、4K超高清HDMI编码器
视频使用操作说明书-T80002系列视频编码器如何对接海康NVR硬盘录像机,包括T80002系列高清HDMI编码器、4K超高清HDMI编码器。 视频使用操作说明书-T80002系列视频编码器如何对接海康NVR硬盘录像机,包括T80002系列高清HDMI编码器、4K超高清HDMI编码器 同三…...

el-input-number计数器change事件校验数据,改变绑定数据值后change方法失效问题的原因及解决方法
在change事件中如果对el-input-number绑定的数据进行更改,会出现change事件失效的问题 试过:this.$set()及赋值等方法,都无法解决 解决方法:用$nextTick函数对绑定值进行更改( this.$nextTick(() > { this.绑定…...

将vue项目整合到springboot项目中并在阿里云上运行
第一步,使用springboot中的thymeleaf模板引擎 导入依赖 <!-- thymeleaf 模板 --><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-thymeleaf</artifactId></dependency> 在r…...
A~C)
AC修炼计划(AtCoder Regular Contest 179)A~C
A - Partition A题传送门 这道题不难发现,如果数字最终的和大于等于K,我们可以把这个原数列从大到小排序,得到最终答案。 如果和小于K,则从小到大排序,同时验证是否符合要求。 #pragma GCC optimize(3) //O2优化开启…...

开发编码规范笔记
前言 (1)该博客仅用于个人笔记 格式转换 (1)查看是 LF 行尾还是CRLF 行尾。 # 单个文件,\n 表示 LF 行尾。\r\n 表示 CRLF 行尾。 hexdump -c <yourfile> # 单个文件,$ 表示 LF 行尾。^M$ 表示 CRLF …...

spring boot easyexcel
1.pom <!-- easyexcel 依赖 --><dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>3.1.1</version></dependency><dependency><groupId>org.projectlombok</group…...

Docker 部署 ShardingSphere-Proxy 数据库中间件
文章目录 Github官网文档ShardingSphere-Proxymysql-connector-java 驱动下载conf 配置global.yamldatabase-sharding.yamldatabase-readwrite-splitting.yamldockerdocker-compose.yml Apache ShardingSphere 是一款分布式的数据库生态系统, 可以将任意数据库转换为…...

Qt常用快捷键
Qt中的常用快捷键 F1查看帮助F2快速到变量声明 从cpp→hShift F2 函数的声明和定义之间快速切换 ;选中函数名 ,从h→cppF4在 cpp 和 h 文件切换 Shift F4在cpp/h文件与 界面文件中切换Ctrl /注释当前行 或者选中的区域Ctrl I自动缩进当前…...

关于RiboSeq分析流程的总结
最近关注了一下RiboSeq的分析方法,方法挺多的,但是无论哪种软件,都会存在或多或少的问题,一点问题不存在的软件不存在,问题的原因出在,1.有的脚本是用python2编写的,目前python2已经不能用了 2.…...

NLP任务:情感分析、看图说话
我可不向其他博主那样拖泥带水,我有代码就直接贴在文章里,或者放到gitee供你们参考下载,虽然写的不咋滴,废话少说,上代码。 gitee码云地址: 卢东艺/pytorch_cv_nlp - 码云 - 开源中国 (gitee.com)https:/…...
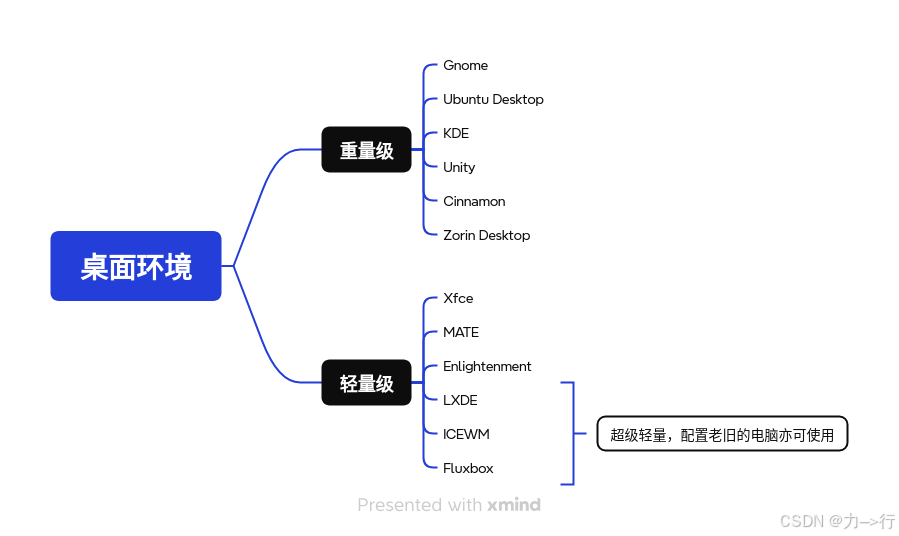
Linux桌面溯源
X窗口系统(X Window System) Linux起源于X窗口系统(X Window System),亦即常说的X11,因其版本止于11之故。 X窗口系统(X Window System,也常称为X11或X)是一种以位图方式显示的软件窗口系统。…...

深入Linux:权限管理与常用命令详解
文章目录 ❤️Linux常用指令🩷zip/unzip指令🩷tar指令🩷bc指令🩷uname指令🩷shutdown指令 ❤️shell命令以及原理❤️什么是 Shell 命令❤️Linux权限管理的概念❤️Linux权限管理🩷文件访问者的分类&#…...

Mojo 编程语言:AI开发者的新宠儿
Mojo(Meta Object Oriented programming for Java Objects)是一种面向对象的编程语言,旨在简化和加速Java应用程序的开发过程。作为近年来新兴的编程语言,Mojo因其与Java的紧密集成以及AI开发领域的应用潜力而逐渐成为AI开发者的新…...
:极氪)
ARM/Linux嵌入式面经(十):极氪
开篇强调两个事情: pdf文件都在百度网盘群:911289806一定要把超链接里面的文章看了,那都是为了你们写的。老板!!!现在多学点,涨个2k工资,真的很值得。要不吃学习的苦,要不吃生活的苦。 1. 自我介绍 专开新篇,等我! 2. 项目介绍,提问 专开新篇,等我! 3. SPI通信和…...
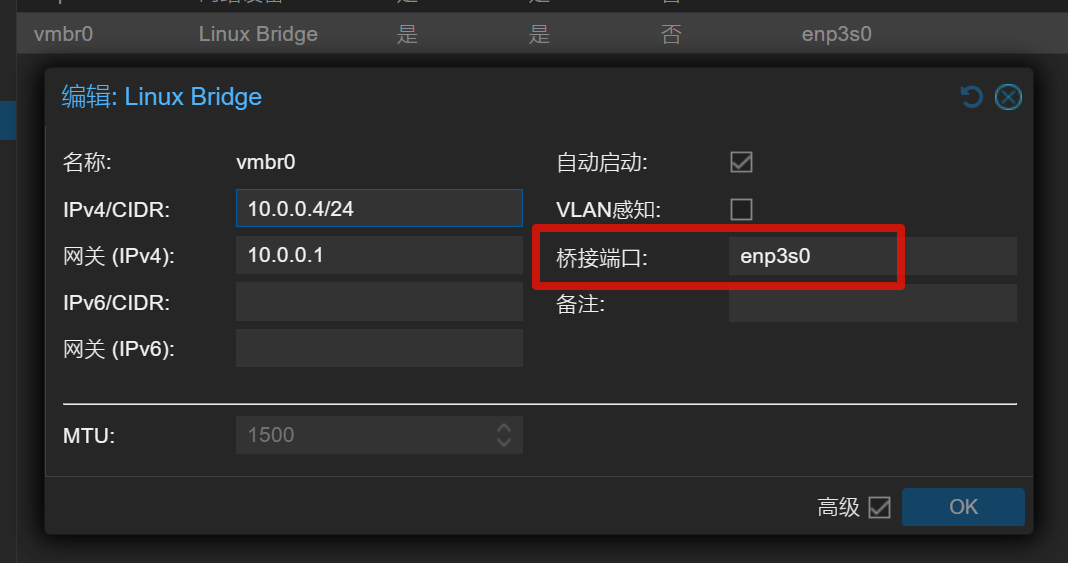
【PVE】新增2.5G网卡作为主网卡暨iperf测速流程
【PVE】新增2.5G网卡作为主网卡暨iperf测速流程 新增网卡 新增网卡的首先当然需要关闭PVE母机,把新网卡插上,我用淘宝遥现金搞了个红包,花了26元买了块SSU的2.5G网卡。说实话这个价位连散热片都没有,确实挺丐的。稍后测下速度看…...

数学建模美赛入门
数学建模需要的学科知识 高等数学线性代数 有很多算法的掌握是需要高等数学和线代的相关知识 如:灰色预测模型需要微积分知识;神经网络需要用到导数知识;图论和层次分析法等都需要用到矩阵计算的相关知识等; 概率论与数理统计&am…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...

手动给中文分词和 直接用神经网络RNN做有什么区别
手动分词和基于神经网络(如 RNN)的自动分词在原理、实现方式和效果上有显著差异,以下是核心对比: 1. 实现原理对比 对比维度手动分词(规则 / 词典驱动)神经网络 RNN 分词(数据驱动)…...
