AC修炼计划(AtCoder Regular Contest 179)A~C
A - Partition
A题传送门
这道题不难发现,如果数字最终的和大于等于K,我们可以把这个原数列从大到小排序,得到最终答案。
如果和小于K,则从小到大排序,同时验证是否符合要求。
#pragma GCC optimize(3) //O2优化开启
#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> PII;
// const int mod=1e9+7;
const int MX=0x3f3f3f3f3f3f3f3f;
//inline int read() //快读
//{
// int xr=0,F=1; char cr;
// while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
// while(cr>='0'&&cr<='9')
// xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
// return xr*F;
//}
//void write(int x) //快写
//{
// if(x<0) putchar('-'),x=-x;
// if(x>9) write(x/10); putchar(x%10+'0');
//}
// 比 unordered_map 更快的哈希表
// #include <ext/pb_ds/assoc_container.hpp>
// using namespace __gnu_pbds;
// const int RANDOM = chrono::high_resolution_clock::now().time_since_epoch().count();
// struct chash {
// int operator()(int x) const { return x ^ RANDOM; }
// };
// typedef gp_hash_table<int, int, chash> hash_t;
constexpr ll mod = 1e9 + 7; //此处为自动取模的数
class modint{ll num;
public:modint(ll num = 0) :num(num % mod){}ll val() const {return num;}modint pow(ll other) {modint res(1), temp = *this;while(other) {if(other & 1) res = res * temp;temp = temp * temp;other >>= 1;}return res;}constexpr ll norm(ll num) const {if (num < 0) num += mod;if (num >= mod) num -= mod;return num;}modint inv(){ return pow(mod - 2); }modint operator+(modint other){ return modint(num + other.num); }modint operator-(){ return { -num }; }modint operator-(modint other){ return modint(-other + *this); }modint operator*(modint other){ return modint(num * other.num); }modint operator/(modint other){ return *this * other.inv(); }modint &operator*=(modint other) { num = num * other.num % mod; return *this; }modint &operator+=(modint other) { num = norm(num + other.num); return *this; }modint &operator-=(modint other) { num = norm(num - other.num); return *this; }modint &operator/=(modint other) { return *this *= other.inv(); }friend istream& operator>>(istream& is, modint& other){ is >> other.num; other.num %= mod; return is; }friend ostream& operator<<(ostream& os, modint other){ other.num = (other.num + mod) % mod; return os << other.num; }
};int n,k;
int a[500005];
void icealsoheat(){cin>>n>>k;for(int i=1;i<=n;i++)cin>>a[i];// sort(a+1,a+1+n);if(k<=0){int sum=0;for(int i=1;i<=n;i++){sum+=a[i];}if(sum>=k){cout<<"Yes\n";sort(a+1,a+1+n,[&](int x,int y){return x>y;});for(int i=1;i<=n;i++){cout<<a[i]<<" ";}}else{cout<<"No\n";}}else{cout<<"Yes\n";sort(a+1,a+1+n);for(int i=1;i<=n;i++){cout<<a[i]<<" ";}}}
signed main(){ios::sync_with_stdio(false); //int128不能用快读!!!!!!cin.tie();cout.tie();int _yq;_yq=1;// cin>>_yq;while(_yq--){icealsoheat();}
}
//
//⠀⠀⠀ ⠀⢸⣿⣿⣿⠀⣼⣿⣿⣦⡀
//⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⠀⠀⠀ ⠀⢸⣿⣿⡟⢰⣿⣿⣿⠟⠁
//⠀⠀⠀⠀⠀⠀⠀⢰⣿⠿⢿⣦⣀⠀⠘⠛⠛⠃⠸⠿⠟⣫⣴⣶⣾⡆
//⠀⠀⠀⠀⠀⠀⠀⠸⣿⡀⠀⠉⢿⣦⡀⠀⠀⠀⠀⠀⠀ ⠛⠿⠿⣿⠃
//⠀⠀⠀⠀⠀⠀⠀⠀⠙⢿⣦⠀⠀⠹⣿⣶⡾⠛⠛⢷⣦⣄⠀
//⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣧⠀⠀⠈⠉⣀⡀⠀ ⠀⠙⢿⡇
//⠀⠀⠀⠀⠀⠀⢀⣠⣴⡿⠟⠋⠀⠀⢠⣾⠟⠃⠀⠀⠀⢸⣿⡆
//⠀⠀⠀⢀⣠⣶⡿⠛⠉⠀⠀⠀⠀⠀⣾⡇⠀⠀⠀⠀⠀⢸⣿⠇
//⢀⣠⣾⠿⠛⠁⠀⠀⠀⠀⠀⠀⠀⢀⣼⣧⣀⠀⠀⠀⢀⣼⠇
//⠈⠋⠁⠀⠀⠀⠀⠀⠀⠀⠀⢀⣴⡿⠋⠙⠛⠛⠛⠛⠛⠁
//⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⣾⡿⠋⠀
//⠀⠀⠀⠀⠀⠀⠀⠀⢾⠿⠋⠀
//B - Between B and B
B题传送门
想了半天没搞出来,后来看了大佬的题解提示才恍然大悟。
这题可以用dp的思想去求,通过题目的数据,我们可以大胆去猜,首先复杂度一定要带个n,其次m仅仅等于10也让我们可以发散性的去想到状压的 2 10 2^{10} 210的复杂度,还可以再添一个m,所以最终的复杂度最多为O(nmlog 2 10 2^{10} 210)。
我们可通过状压来枚举各个数是否符合条件可以放入的情况。比如第i位,假如我向这个数位放入的数字是j,首先,放入j的前提条件是在当前位数和上一个放入j的位数之间我们放入了至少一个a[j],此时j可以放入,同时,放入了j后,j会使得后面所有a[x]=j的数字都可以放入,我们可以通过状态去枚举各个数字是否可以放入,能放入的话对应的二进制位数就是1,不能放入就是0。
#pragma GCC optimize(3) //O2优化开启
#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> PII;
// const int mod=1e9+7;
const int MX=0x3f3f3f3f3f3f3f3f;
//inline int read() //快读
//{
// int xr=0,F=1; char cr;
// while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
// while(cr>='0'&&cr<='9')
// xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
// return xr*F;
//}
//void write(int x) //快写
//{
// if(x<0) putchar('-'),x=-x;
// if(x>9) write(x/10); putchar(x%10+'0');
//}
// 比 unordered_map 更快的哈希表
// #include <ext/pb_ds/assoc_container.hpp>
// using namespace __gnu_pbds;
// const int RANDOM = chrono::high_resolution_clock::now().time_since_epoch().count();
// struct chash {
// int operator()(int x) const { return x ^ RANDOM; }
// };
// typedef gp_hash_table<int, int, chash> hash_t;
constexpr ll mod = 998244353; //此处为自动取模的数
class modint{ll num;
public:modint(ll num = 0) :num(num % mod){}ll val() const {return num;}modint pow(ll other) {modint res(1), temp = *this;while(other) {if(other & 1) res = res * temp;temp = temp * temp;other >>= 1;}return res;}constexpr ll norm(ll num) const {if (num < 0) num += mod;if (num >= mod) num -= mod;return num;}modint inv(){ return pow(mod - 2); }modint operator+(modint other){ return modint(num + other.num); }modint operator-(){ return { -num }; }modint operator-(modint other){ return modint(-other + *this); }modint operator*(modint other){ return modint(num * other.num); }modint operator/(modint other){ return *this * other.inv(); }modint &operator*=(modint other) { num = num * other.num % mod; return *this; }modint &operator+=(modint other) { num = norm(num + other.num); return *this; }modint &operator-=(modint other) { num = norm(num - other.num); return *this; }modint &operator/=(modint other) { return *this *= other.inv(); }friend istream& operator>>(istream& is, modint& other){ is >> other.num; other.num %= mod; return is; }friend ostream& operator<<(ostream& os, modint other){ other.num = (other.num + mod) % mod; return os << other.num; }
};int n,m;
int a[50005];
modint dp[20005][2000];
int id[50005];
void icealsoheat(){int m,n;cin>>n>>m;for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<=n;i++){id[a[i]]|=(1<<(i-1));}// for(int i=0;i<n;i++)dp[0][1<<i]=1;dp[0][(1<<n)-1]=1;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){for(int o=0;o<(1<<n);o++){if(o>>(j-1)&1){int x=o;x-=(1<<(j-1));x|=id[j];dp[i][x]+=dp[i-1][o];}}}}modint ans=0;for(int i=0;i<(1<<n);i++)ans+=dp[m][i];cout<<ans;}
signed main(){ios::sync_with_stdio(false); //int128不能用快读!!!!!!cin.tie();cout.tie();int _yq;_yq=1;// cin>>_yq;while(_yq--){icealsoheat();}
}
//
//⠀⠀⠀ ⠀⢸⣿⣿⣿⠀⣼⣿⣿⣦⡀
//⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⠀⠀⠀ ⠀⢸⣿⣿⡟⢰⣿⣿⣿⠟⠁
//⠀⠀⠀⠀⠀⠀⠀⢰⣿⠿⢿⣦⣀⠀⠘⠛⠛⠃⠸⠿⠟⣫⣴⣶⣾⡆
//⠀⠀⠀⠀⠀⠀⠀⠸⣿⡀⠀⠉⢿⣦⡀⠀⠀⠀⠀⠀⠀ ⠛⠿⠿⣿⠃
//⠀⠀⠀⠀⠀⠀⠀⠀⠙⢿⣦⠀⠀⠹⣿⣶⡾⠛⠛⢷⣦⣄⠀
//⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣧⠀⠀⠈⠉⣀⡀⠀ ⠀⠙⢿⡇
//⠀⠀⠀⠀⠀⠀⢀⣠⣴⡿⠟⠋⠀⠀⢠⣾⠟⠃⠀⠀⠀⢸⣿⡆
//⠀⠀⠀⢀⣠⣶⡿⠛⠉⠀⠀⠀⠀⠀⣾⡇⠀⠀⠀⠀⠀⢸⣿⠇
//⢀⣠⣾⠿⠛⠁⠀⠀⠀⠀⠀⠀⠀⢀⣼⣧⣀⠀⠀⠀⢀⣼⠇
//⠈⠋⠁⠀⠀⠀⠀⠀⠀⠀⠀⢀⣴⡿⠋⠙⠛⠛⠛⠛⠛⠁
//⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⣾⡿⠋⠀
//⠀⠀⠀⠀⠀⠀⠀⠀⢾⠿⠋⠀
//C - Beware of Overflow
C题传送门
还是我太菜了,看题目都费劲,最后还是不争气的看了题解,竟然题解把查询放入了排序的cmp函数中,确实还是我自己的思维太局限了,容易想到的是,我们把所有的数从小到大排序,然后头尾相加,再把相加的数通过二分按顺序放入这个数中,重复上述操作,知道符合最后条件为止,O(nlogn)的复杂度,所以不会超过25000次询问。
#pragma GCC optimize(3) //O2优化开启
#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> PII;
// const int mod=1e9+7;
const int MX=0x3f3f3f3f3f3f3f3f;
//inline int read() //快读
//{
// int xr=0,F=1; char cr;
// while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
// while(cr>='0'&&cr<='9')
// xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
// return xr*F;
//}
//void write(int x) //快写
//{
// if(x<0) putchar('-'),x=-x;
// if(x>9) write(x/10); putchar(x%10+'0');
//}
// 比 unordered_map 更快的哈希表
// #include <ext/pb_ds/assoc_container.hpp>
// using namespace __gnu_pbds;
// const int RANDOM = chrono::high_resolution_clock::now().time_since_epoch().count();
// struct chash {
// int operator()(int x) const { return x ^ RANDOM; }
// };
// typedef gp_hash_table<int, int, chash> hash_t;
constexpr ll mod = 998244353; //此处为自动取模的数
class modint{ll num;
public:modint(ll num = 0) :num(num % mod){}ll val() const {return num;}modint pow(ll other) {modint res(1), temp = *this;while(other) {if(other & 1) res = res * temp;temp = temp * temp;other >>= 1;}return res;}constexpr ll norm(ll num) const {if (num < 0) num += mod;if (num >= mod) num -= mod;return num;}modint inv(){ return pow(mod - 2); }modint operator+(modint other){ return modint(num + other.num); }modint operator-(){ return { -num }; }modint operator-(modint other){ return modint(-other + *this); }modint operator*(modint other){ return modint(num * other.num); }modint operator/(modint other){ return *this * other.inv(); }modint &operator*=(modint other) { num = num * other.num % mod; return *this; }modint &operator+=(modint other) { num = norm(num + other.num); return *this; }modint &operator-=(modint other) { num = norm(num - other.num); return *this; }modint &operator/=(modint other) { return *this *= other.inv(); }friend istream& operator>>(istream& is, modint& other){ is >> other.num; other.num %= mod; return is; }friend ostream& operator<<(ostream& os, modint other){ other.num = (other.num + mod) % mod; return os << other.num; }
};
int n;
bool cmp(int a,int b){cout<<"? "<<a<<" "<<b<<endl;int s;cin>>s;return s;
}
// bool check(int p,int o){
// cout<<"? "<<p<<" "<<o<<endl;
// int x;
// cin>>x;
// return x==0;
// }
void icealsoheat(){cin>>n;vector<int>ve;for(int i=1;i<=n;i++){ve.push_back(i);}sort(ve.begin(),ve.end(),cmp);while(ve.size()>1){int le=ve[0];int re=ve.back();// int x=le+re;cout<<"+ "<<le<<" "<<re<<endl;int x;cin>>x;ve.erase(ve.begin());ve.pop_back();// cout<<"+"<<iif(ve.size()==0){break;}int l=0,r=ve.size()-1;int mid;while(l<r){mid=(l+r)>>1;if(cmp(x,ve[mid]))r=mid;else l=mid+1;}if(!cmp(x,ve[l]))l++;ve.insert(ve.begin()+l,x);}cout<<"!"<<endl;
}
signed main(){ios::sync_with_stdio(false); //int128不能用快读!!!!!!cin.tie();cout.tie();int _yq;_yq=1;// cin>>_yq;while(_yq--){icealsoheat();}
}
//
//⠀⠀⠀ ⠀⢸⣿⣿⣿⠀⣼⣿⣿⣦⡀
//⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⠀⠀⠀ ⠀⢸⣿⣿⡟⢰⣿⣿⣿⠟⠁
//⠀⠀⠀⠀⠀⠀⠀⢰⣿⠿⢿⣦⣀⠀⠘⠛⠛⠃⠸⠿⠟⣫⣴⣶⣾⡆
//⠀⠀⠀⠀⠀⠀⠀⠸⣿⡀⠀⠉⢿⣦⡀⠀⠀⠀⠀⠀⠀ ⠛⠿⠿⣿⠃
//⠀⠀⠀⠀⠀⠀⠀⠀⠙⢿⣦⠀⠀⠹⣿⣶⡾⠛⠛⢷⣦⣄⠀
//⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣧⠀⠀⠈⠉⣀⡀⠀ ⠀⠙⢿⡇
//⠀⠀⠀⠀⠀⠀⢀⣠⣴⡿⠟⠋⠀⠀⢠⣾⠟⠃⠀⠀⠀⢸⣿⡆
//⠀⠀⠀⢀⣠⣶⡿⠛⠉⠀⠀⠀⠀⠀⣾⡇⠀⠀⠀⠀⠀⢸⣿⠇
//⢀⣠⣾⠿⠛⠁⠀⠀⠀⠀⠀⠀⠀⢀⣼⣧⣀⠀⠀⠀⢀⣼⠇
//⠈⠋⠁⠀⠀⠀⠀⠀⠀⠀⠀⢀⣴⡿⠋⠙⠛⠛⠛⠛⠛⠁
//⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⣾⡿⠋⠀
//⠀⠀⠀⠀⠀⠀⠀⠀⢾⠿⠋⠀
//相关文章:
A~C)
AC修炼计划(AtCoder Regular Contest 179)A~C
A - Partition A题传送门 这道题不难发现,如果数字最终的和大于等于K,我们可以把这个原数列从大到小排序,得到最终答案。 如果和小于K,则从小到大排序,同时验证是否符合要求。 #pragma GCC optimize(3) //O2优化开启…...

开发编码规范笔记
前言 (1)该博客仅用于个人笔记 格式转换 (1)查看是 LF 行尾还是CRLF 行尾。 # 单个文件,\n 表示 LF 行尾。\r\n 表示 CRLF 行尾。 hexdump -c <yourfile> # 单个文件,$ 表示 LF 行尾。^M$ 表示 CRLF …...

spring boot easyexcel
1.pom <!-- easyexcel 依赖 --><dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>3.1.1</version></dependency><dependency><groupId>org.projectlombok</group…...

Docker 部署 ShardingSphere-Proxy 数据库中间件
文章目录 Github官网文档ShardingSphere-Proxymysql-connector-java 驱动下载conf 配置global.yamldatabase-sharding.yamldatabase-readwrite-splitting.yamldockerdocker-compose.yml Apache ShardingSphere 是一款分布式的数据库生态系统, 可以将任意数据库转换为…...

Qt常用快捷键
Qt中的常用快捷键 F1查看帮助F2快速到变量声明 从cpp→hShift F2 函数的声明和定义之间快速切换 ;选中函数名 ,从h→cppF4在 cpp 和 h 文件切换 Shift F4在cpp/h文件与 界面文件中切换Ctrl /注释当前行 或者选中的区域Ctrl I自动缩进当前…...

关于RiboSeq分析流程的总结
最近关注了一下RiboSeq的分析方法,方法挺多的,但是无论哪种软件,都会存在或多或少的问题,一点问题不存在的软件不存在,问题的原因出在,1.有的脚本是用python2编写的,目前python2已经不能用了 2.…...

NLP任务:情感分析、看图说话
我可不向其他博主那样拖泥带水,我有代码就直接贴在文章里,或者放到gitee供你们参考下载,虽然写的不咋滴,废话少说,上代码。 gitee码云地址: 卢东艺/pytorch_cv_nlp - 码云 - 开源中国 (gitee.com)https:/…...
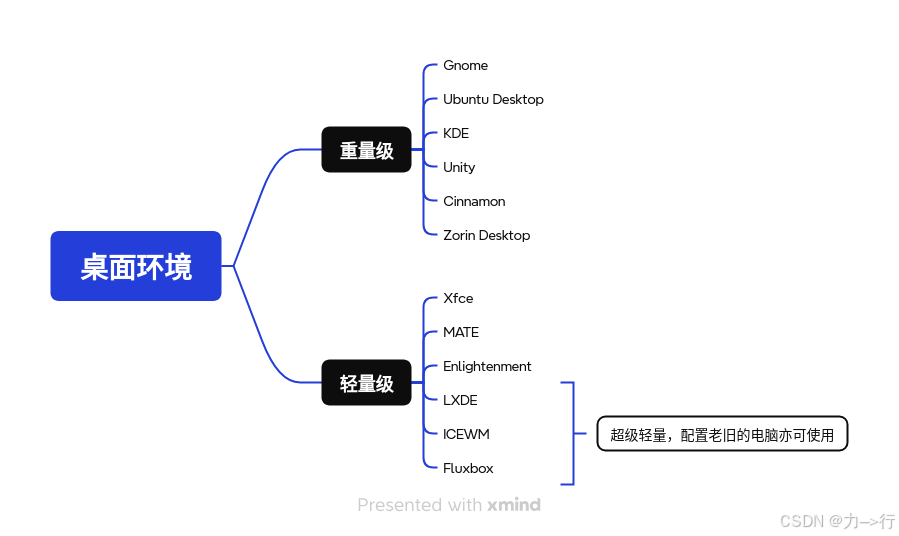
Linux桌面溯源
X窗口系统(X Window System) Linux起源于X窗口系统(X Window System),亦即常说的X11,因其版本止于11之故。 X窗口系统(X Window System,也常称为X11或X)是一种以位图方式显示的软件窗口系统。…...

深入Linux:权限管理与常用命令详解
文章目录 ❤️Linux常用指令🩷zip/unzip指令🩷tar指令🩷bc指令🩷uname指令🩷shutdown指令 ❤️shell命令以及原理❤️什么是 Shell 命令❤️Linux权限管理的概念❤️Linux权限管理🩷文件访问者的分类&#…...

Mojo 编程语言:AI开发者的新宠儿
Mojo(Meta Object Oriented programming for Java Objects)是一种面向对象的编程语言,旨在简化和加速Java应用程序的开发过程。作为近年来新兴的编程语言,Mojo因其与Java的紧密集成以及AI开发领域的应用潜力而逐渐成为AI开发者的新…...
:极氪)
ARM/Linux嵌入式面经(十):极氪
开篇强调两个事情: pdf文件都在百度网盘群:911289806一定要把超链接里面的文章看了,那都是为了你们写的。老板!!!现在多学点,涨个2k工资,真的很值得。要不吃学习的苦,要不吃生活的苦。 1. 自我介绍 专开新篇,等我! 2. 项目介绍,提问 专开新篇,等我! 3. SPI通信和…...
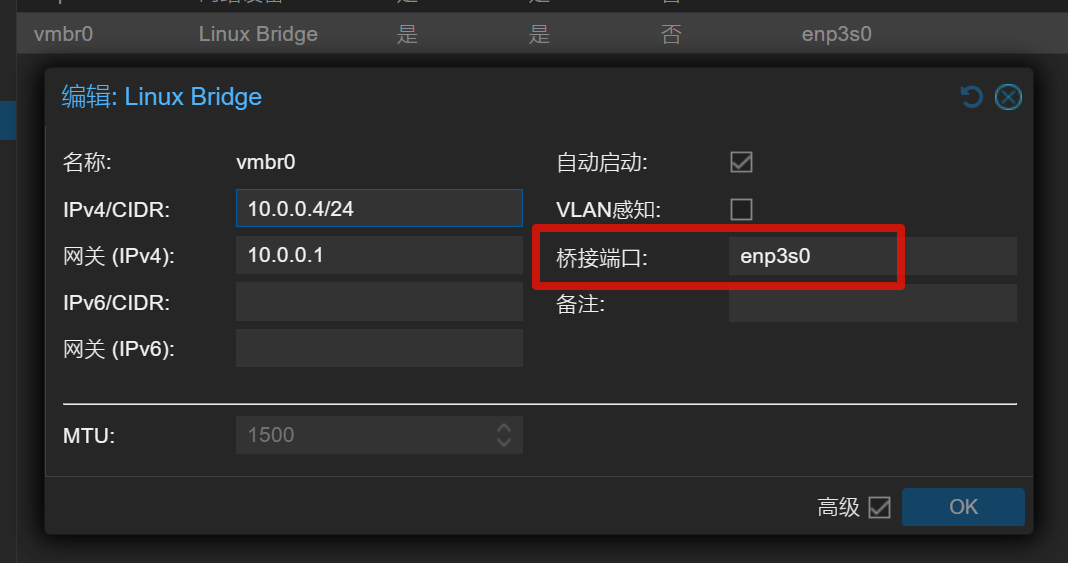
【PVE】新增2.5G网卡作为主网卡暨iperf测速流程
【PVE】新增2.5G网卡作为主网卡暨iperf测速流程 新增网卡 新增网卡的首先当然需要关闭PVE母机,把新网卡插上,我用淘宝遥现金搞了个红包,花了26元买了块SSU的2.5G网卡。说实话这个价位连散热片都没有,确实挺丐的。稍后测下速度看…...

数学建模美赛入门
数学建模需要的学科知识 高等数学线性代数 有很多算法的掌握是需要高等数学和线代的相关知识 如:灰色预测模型需要微积分知识;神经网络需要用到导数知识;图论和层次分析法等都需要用到矩阵计算的相关知识等; 概率论与数理统计&am…...

两段序列帧动画播放,在ios机型上出现闪屏
使用场景:两段序列帧动画连接播放,先播放第一段播一次,再播放第二段,第二段循环播放,在ios机型上出现动画闪动,播放不正常。 错误的写法:把每一段序列帧动画单独写在了定义的动画里 .gacha-bg…...

【C++深度探索】全面解析多态性机制(二)
🔥 个人主页:大耳朵土土垚 🔥 所属专栏:C从入门至进阶 这里将会不定期更新有关C/C的内容,欢迎大家点赞,收藏,评论🥳🥳🎉🎉🎉 前言 我…...

MySQL配置数据库的连接命令
MySQL配置数据库连接命令 在MySQL中,配置数据库连接的命令涉及创建用户、授予权限、配置主从复制等多个方面。以下是常用的命令及其用途: 创建用户 创建一个新的数据库用户并为其设置密码: CREATE USER usernamehost IDENTIFIED BY passwo…...

[PaddlePaddle飞桨] PaddleSpeech-自动语音识别-小模型部署
PaddleSpeech的GitHub项目地址 环境要求: gcc > 4.8.5 paddlepaddle < 2.5.1 python > 3.8 OS support: Linux(recommend), Windows, Mac OSXpip下载指令: python -m pip install paddlepaddle-gpu2.5.1 -i https://pypi.tuna.tsinghua.edu.c…...
)
redis查询慢,你们是如何排查优化的?(总结篇)
1,先进行基准测试,查看redis是否存在查询过慢情况,根据自己的情况而定 2、检查网络连接是否出现延迟,数据丢包问题(可能性小 3、开启慢查询日志,通过日志可以清楚知道哪些命令比较耗时,同时避…...

Docker 容器出现 IP 冲突
Docker 容器出现 IP 冲突的情况可能由以下几个原因导致: 静态 IP 分配:如果你在 docker-compose.yml 文件中为多个容器手动设置了相同的静态 IP 地址,那么这些容器在启动时就会出现 IP 冲突。确保每个容器分配的静态 IP 地址是唯一的。桥接网…...

paddlepaddle2.6,paddleorc2.8,cuda12,cudnn,nccl,python10环境
1.安装英伟达显卡驱动 首先需要到NAVIDIA官网去查自己的电脑是不是支持GPU运算。 网址是:CUDA GPUs | NVIDIA Developer。打开后的界面大致如下,只要里边有对应的型号就可以用GPU运算,并且每一款设备都列出来相关的计算能力(Compu…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...
