数学建模中的辅助变量、中间变量、指示变量
在数学建模中,除了决策变量外,还有一些其他类型的变量,如中间变量、辅助变量和指示变量。每种变量在模型中都有特定的用途和意义。以下是对这些变量的详细解释:
1. 决策变量(Decision Variables)
- 定义:决策变量是模型中需要优化的变量,它们代表了决策者可以控制的量。
- 用途:决策变量是数学模型的核心,通过优化这些变量来达到目标(如最小化成本或最大化利润)。
- 示例:
- 在生产计划问题中,决策变量可以是每种产品的生产数量。
- 在运输问题中,决策变量可以是每条运输路径上的货物数量。
2. 中间变量(Intermediate Variables)
-
定义:中间变量是模型中用于计算的变量,它们通常是决策变量的函数,用于简化模型的表达或计算。
-
用途:中间变量帮助分解复杂的计算过程,使模型更易于理解和求解。
-
示例:
- 在生产计划问题中,中间变量可以是总生产成本,它是各产品生产数量和单位成本的乘积之和。
- 在网络流问题中,中间变量可以是某条路径上的总流量,它是各段流量的和。
3. 辅助变量(Auxiliary Variables)
- 定义:辅助变量是模型中引入的额外变量,用于简化约束条件或目标函数的表达。
- 用途:辅助变量可以帮助将复杂的非线性约束或目标函数转化为线性形式,便于求解。
- 示例:
- 在线性规划中,辅助变量可以用于将绝对值函数转化为线性形式。
- 在整数规划中,辅助变量可以用于表示某些逻辑条件或约束。
4. 指示变量(Indicator Variables)
- 定义:指示变量(也称为二进制变量或0-1变量)是取值为0或1的变量,用于表示某种状态或决策的存在与否。
- 用途:指示变量常用于表示是否选择某个选项、是否满足某个条件等。
- 示例:
- 在设施选址问题中,指示变量可以表示某个设施是否被选址。
- 在项目调度问题中,指示变量可以表示某个任务是否在某个时间段内执行。
示例
示例
假设我们有一个生产计划问题,需要最小化生产成本,同时满足需求和资源限制。我们可以定义以下变量:
- 决策变量: x i x_i xi,生产第 i i i种产品的数量。
- 中间变量:总生产成本 TotalCost \text{TotalCost} TotalCost,计算公式为 TotalCost = ∑ i c i x i \text{TotalCost} = \sum_{i} c_i x_i TotalCost=∑icixi,其中 c i c_i ci是第 i i i种产品的单位成本。
- 辅助变量: y i y_i yi:辅助变量,用于将非线性约束转化为线性形式。例如,如果我们有一个约束 ∣ x i − d i ∣ ≤ M |x_i - d_i| \leq M ∣xi−di∣≤M,可以引入辅助变量 y i y_i yi 使得 y i ≥ x i − d i y_i \geq x_i - d_i yi≥xi−di 和 y i ≥ d i − x i y_i \geq d_i - x_i yi≥di−xi,并添加约束 y i ≤ M y_i \leq M yi≤M。
指示变量: z i z_i zi:指示变量,表示是否生产第 i i i 种产品。 z i z_i zi取值为0或1。如果 z i = 1 z_i = 1 zi=1,则生产第 i i i 种产品;如果 z i = 0 z_i = 0 zi=0,则不生产第 i i i 种产品。
综合上述变量,我们可以构建一个数学模型:
目标函数:
min TotalCost = ∑ i c i x i \min \text{TotalCost} = \sum_{i} c_i x_i minTotalCost=∑icixi
约束条件:
- 需求约束: x i ≥ d i x_i \geq d_i xi≥di
- 资源约束: ∑ i r i x i ≤ R \sum_{i} r_i x_i \leq R ∑irixi≤R
- 辅助变量约束: y i ≥ x i − d i , y i ≥ d i − x i , y i ≤ M y_i \geq x_i - d_i ,y_i \geq d_i - x_i ,y_i \leq M yi≥xi−di,yi≥di−xi,yi≤M
- 指示变量约束: x i ≤ M z i x_i \leq M z_i xi≤Mzi,其中 M 是一个足够大的常数
通过这种方式,我们可以使用不同类型的变量来构建和优化数学模型。每种变量在模型中都有特定的用途和意义,帮助我们更好地表达和求解实际问题。
相关文章:

数学建模中的辅助变量、中间变量、指示变量
在数学建模中,除了决策变量外,还有一些其他类型的变量,如中间变量、辅助变量和指示变量。每种变量在模型中都有特定的用途和意义。以下是对这些变量的详细解释: 1. 决策变量(Decision Variables) 定义&am…...
和tell())
python的seek()和tell()
seek() seek() 是用来在文件中移动指针位置的方法。它的作用是将文件内部的当前位置设置为指定的位置。 seek(offset, whence) 参数说明 offset: 这是一个整数值,表示相对于起始位置的偏移量。如果是正数,表示向文件末尾方向移动;如果是负…...

Go泛型详解
引子 如果我们要写一个函数分别比较2个整数和浮点数的大小,我们就要写2个函数。如下: func Min(x, y float64) float64 {if x < y {return x}return y }func MinInt(x, y int) int {if x < y {return x}return y }2个函数,除了数据类…...

【每日一练】python之sum()求和函数实例讲解
在Python中, sum()是一个内置函数,用于计算可迭代对象(如列表、元组等)中所有元素的总和。如下实例: """ 收入支出统计小程序 知识点:用户输入获取列表元素添加sum()函数,统计作用 "&…...

打造智慧校园德育管理,提升学生操行基础分
智慧校园的德育管理系统内嵌的操行基础分功能,是对学生日常行为规范和道德素养进行量化评估的一个创新实践。该功能通过将抽象的道德品质转化为具体可量化的指标,如遵守纪律、尊师重道、团结协作、爱护环境及参与集体活动的积极性等,为每个学…...

自定义函数---随机数系列函数
大家有没有发现平常在写随机数的时候,需要引入很多的头文件,然后还需要用一些复杂的函数,大家可能不太习惯,于是我就制作了一个头文件 // random_number.h #ifndef RANDOM_NUMBER_H // 预处理指令,防止头文件被重复包含…...
一文了解5G新通话技术演进与业务模型
5G新通话简介 5G新通话,也被称为VoNR,是基于R16及后续协议产生的一种增强型语音通话业务。 它在IMS网络里新增数据通道(Data Channel),承载通话时的文本、图片、涂鸦、菜单等信息。它能在传统话音业务基础上提供更多服…...

视频使用操作说明书-T80002系列视频编码器如何对接海康NVR硬盘录像机,包括T80002系列高清HDMI编码器、4K超高清HDMI编码器
视频使用操作说明书-T80002系列视频编码器如何对接海康NVR硬盘录像机,包括T80002系列高清HDMI编码器、4K超高清HDMI编码器。 视频使用操作说明书-T80002系列视频编码器如何对接海康NVR硬盘录像机,包括T80002系列高清HDMI编码器、4K超高清HDMI编码器 同三…...

el-input-number计数器change事件校验数据,改变绑定数据值后change方法失效问题的原因及解决方法
在change事件中如果对el-input-number绑定的数据进行更改,会出现change事件失效的问题 试过:this.$set()及赋值等方法,都无法解决 解决方法:用$nextTick函数对绑定值进行更改( this.$nextTick(() > { this.绑定…...

将vue项目整合到springboot项目中并在阿里云上运行
第一步,使用springboot中的thymeleaf模板引擎 导入依赖 <!-- thymeleaf 模板 --><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-thymeleaf</artifactId></dependency> 在r…...
A~C)
AC修炼计划(AtCoder Regular Contest 179)A~C
A - Partition A题传送门 这道题不难发现,如果数字最终的和大于等于K,我们可以把这个原数列从大到小排序,得到最终答案。 如果和小于K,则从小到大排序,同时验证是否符合要求。 #pragma GCC optimize(3) //O2优化开启…...

开发编码规范笔记
前言 (1)该博客仅用于个人笔记 格式转换 (1)查看是 LF 行尾还是CRLF 行尾。 # 单个文件,\n 表示 LF 行尾。\r\n 表示 CRLF 行尾。 hexdump -c <yourfile> # 单个文件,$ 表示 LF 行尾。^M$ 表示 CRLF …...

spring boot easyexcel
1.pom <!-- easyexcel 依赖 --><dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>3.1.1</version></dependency><dependency><groupId>org.projectlombok</group…...

Docker 部署 ShardingSphere-Proxy 数据库中间件
文章目录 Github官网文档ShardingSphere-Proxymysql-connector-java 驱动下载conf 配置global.yamldatabase-sharding.yamldatabase-readwrite-splitting.yamldockerdocker-compose.yml Apache ShardingSphere 是一款分布式的数据库生态系统, 可以将任意数据库转换为…...

Qt常用快捷键
Qt中的常用快捷键 F1查看帮助F2快速到变量声明 从cpp→hShift F2 函数的声明和定义之间快速切换 ;选中函数名 ,从h→cppF4在 cpp 和 h 文件切换 Shift F4在cpp/h文件与 界面文件中切换Ctrl /注释当前行 或者选中的区域Ctrl I自动缩进当前…...

关于RiboSeq分析流程的总结
最近关注了一下RiboSeq的分析方法,方法挺多的,但是无论哪种软件,都会存在或多或少的问题,一点问题不存在的软件不存在,问题的原因出在,1.有的脚本是用python2编写的,目前python2已经不能用了 2.…...

NLP任务:情感分析、看图说话
我可不向其他博主那样拖泥带水,我有代码就直接贴在文章里,或者放到gitee供你们参考下载,虽然写的不咋滴,废话少说,上代码。 gitee码云地址: 卢东艺/pytorch_cv_nlp - 码云 - 开源中国 (gitee.com)https:/…...
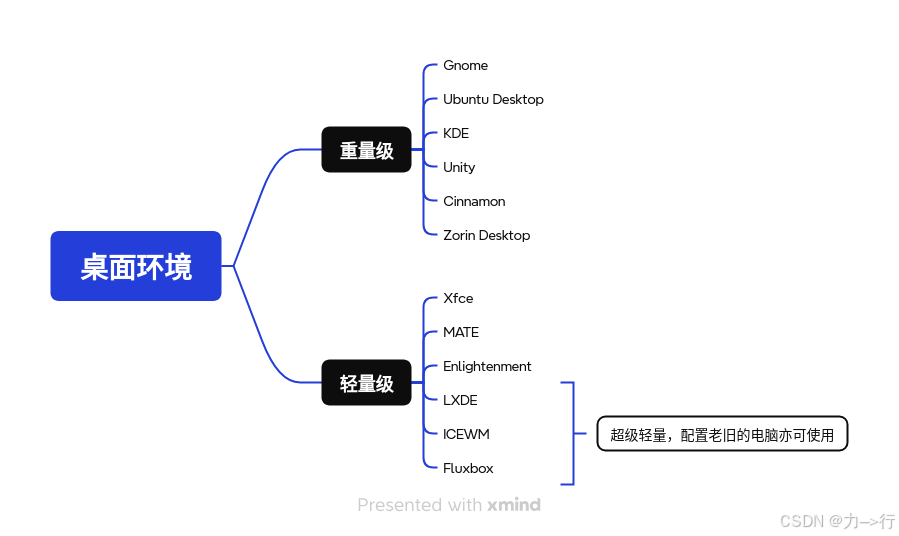
Linux桌面溯源
X窗口系统(X Window System) Linux起源于X窗口系统(X Window System),亦即常说的X11,因其版本止于11之故。 X窗口系统(X Window System,也常称为X11或X)是一种以位图方式显示的软件窗口系统。…...

深入Linux:权限管理与常用命令详解
文章目录 ❤️Linux常用指令🩷zip/unzip指令🩷tar指令🩷bc指令🩷uname指令🩷shutdown指令 ❤️shell命令以及原理❤️什么是 Shell 命令❤️Linux权限管理的概念❤️Linux权限管理🩷文件访问者的分类&#…...

Mojo 编程语言:AI开发者的新宠儿
Mojo(Meta Object Oriented programming for Java Objects)是一种面向对象的编程语言,旨在简化和加速Java应用程序的开发过程。作为近年来新兴的编程语言,Mojo因其与Java的紧密集成以及AI开发领域的应用潜力而逐渐成为AI开发者的新…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
