计算1的数量
1. 计算1的数量
题目ID:9809必做题100分
最新提交:
Accepted
100 分
历史最高:
Accepted
100 分
时间限制: 1000ms
空间限制: 524288kB
题目描述
给定一个n*m的二进制矩阵,请你数一数矩阵中完全被0上下左右包围的1的数目。
输入格式
第一行两个整数n和m(3<=n,m<=100)
接下来n行,每行m个0或1的整数。
输出格式
输出一个整数代表结果
样例
Input 1
4 4
1 0 1 1
0 1 0 0
1 0 1 0
0 0 0 1
Output 1
2
样例解释
样例解释:
样例中有两个1是完全被0包围的。
代码:
#include <bits/stdc++.h>
#include <vector>using namespace std;int main()
{int n, m;cin >> n >> m; // 4 4int cnt = 0;int a[105][105];for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){cin >> a[i][j];}}//for (int i = 2; i <= n - 1; i++){for (int j = 2; j <= m - 1; j++){if (a[i][j] == 1 && a[i - 1][j] == 0 && a[i + 1][j] == 0 && a[i][j - 1] == 0 && a[i][j + 1] == 0){cnt++;}}}cout << cnt << endl;return 0;
}相关文章:

计算1的数量
1. 计算1的数量 题目ID:9809必做题100分 最新提交: Accepted 100 分 历史最高: Accepted 100 分 时间限制: 1000ms 空间限制: 524288kB 题目描述 给定一个n*m的二进制矩阵,请你数一数矩阵中完全被0上下左右包围的1的数…...

Linux udp编程
我最近开了几个专栏,诚信互三! > |||《算法专栏》::刷题教程来自网站《代码随想录》。||| > |||《C专栏》::记录我学习C的经历,看完你一定会有收获。||| > |||《Linux专栏》࿱…...

【开源项目】Rust开发复制文件夹目录结构工具
说明 由于我经常需要在多个大容量的移动硬盘中查找和新增文件,我希望把硬盘的目录结构放到服务器的自建网盘中,因此开发了这个工具,使得在不同硬盘之间的文件管理变得更加便捷 项目地址:https://github.com/VinciYan/folder_clon…...

PostgreSQL的pg_dirtyread工具
PostgreSQL的pg_dirtyread工具 pg_dirtyread 是一个第三方PostgreSQL扩展,它允许用户读取数据库文件中的“脏”数据,即那些被标记为删除或不再可见的数据。这个扩展对于数据恢复和调试非常有用,尤其是在需要恢复被删除或更新前的数据时。 以…...

苹果梦碎:Vision Pro的辉煌与失落,苹果已决定暂停 Vision Pro 后续产品的研发工作
本文首发于公众号“AntDream”,欢迎微信搜索“AntDream”或扫描文章底部二维码关注,和我一起每天进步一点点 苹果Vision Pro:科技巨头的跌宕起伏 在科技的海洋中,苹果公司一直以其创新精神和卓越品质引领潮流。然而,即…...

推荐一款uniapp拖动验证码插件
插件地址:易盾验证码 - DCloud 插件市场 具体使用方式访问插件地址自行获取...

十年期国债收益率
十年期国债收益率是指政府发行的、期限为十年的国债的年化收益率。它被广泛视为一个国家经济健康状况和未来经济前景的重要指标,同时也是金融市场中的一个重要基准利率。 下面我将详细解释十年期国债收益率的相关内容及其意义。 十年期国债收益率的意义 经济健康的…...

使用Go编写的持续下行测速脚本,快速消耗流量且不伤硬盘
GoSpeed 声明 此工具仅用于测试与学习,请勿用于非法用途,如使用此程序请确保所有下载的内容都拥有合法的使用权或分发权,避免侵犯版权、恶意访问 此工具仅用于测试与学习,请勿用于非法用途,如使用此程序请确保所有下载的内容都拥有合法的使用权或分发权,…...

保护国外使用代理IP的安全方法
为了保护在国外使用代理IP的安全,用户可以采取以下方法: 1. 选择可信的代理服务器 在选择代理服务器时,用户应该选择那些经过验证和信任的服务器,如知名的VPN服务提供商。这些服务器通常具有更高的安全性和隐私保护措施。 2. 使用…...

18集 学习ESP32的ESP-DL深度学习教程-《MCU嵌入式AI开发笔记》
18集 学习ESP32的ESP-DL深度学习教程-《MCU嵌入式AI开发笔记》 参考文档:https://docs.espressif.com/projects/esp-dl/zh_CN/latest/esp32/tutorials/index.html 使用TVM自动生成模型部署项目 本案例介绍了使用 TVM 部署模型的完整流程。 该项目基于 TVM v0.14…...

jmeter-beanshell学习9-放弃beanshell
写这篇时候道心不稳了,前面写了好几篇benashell元件,突然发现应该放弃。想回去改前面的文章,看了看无从下手,反正已经这样了,我淋了雨,那就希望别人也没有伞吧,哈哈哈哈,放在第九篇送…...

Web 性能入门指南-1.5 创建 Web 性能优化文化的最佳实践
最成功的网站都有什么共同点?那就是他们都有很强的网站性能和可用性文化。以下是一些经过验证的有效技巧和最佳实践,可帮助您建立健康、快乐、值得庆祝的性能文化。 创建强大的性能优化文化意味着在你的公司或团队中创建一个如下所示的反馈循环ÿ…...
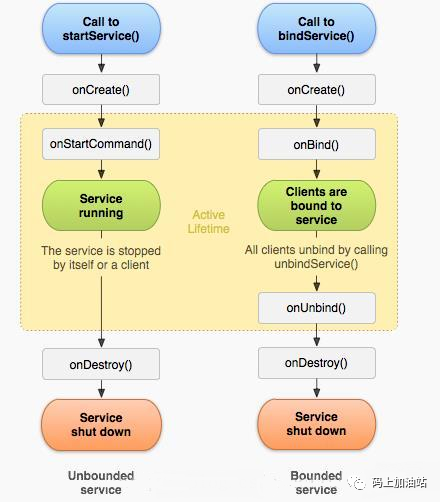
【Android】Service介绍和生命周期
人不走空 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌赋:斯是陋室,惟吾德馨 介绍 Service是Android程序中四大基础组件之一,它和Activity一样都是Context的子类,只不…...

[论文笔记]RAPTOR: RECURSIVE ABSTRACTIVE PROCESSING FOR TREE-ORGANIZED RETRIEVAL
引言 今天带来又一篇RAG论文笔记:RAPTOR: RECURSIVE ABSTRACTIVE PROCESSING FOR TREE-ORGANIZED RETRIEVAL。 检索增强语言模型能够更好地适应世界状态的变化并融入长尾知识。然而,大多数现有方法只能从检索语料库中检索到短的连续文本片段࿰…...

python 端口的转发
实现端口的转发 tcpsocket.py 对基础的socket进行了封装 import socketclass baseSocket:def service(host:str,port:int,maxSuspend:int)->socket: service_socket socket.socket(socket.AF_INET,socket.SOCK_STREAM) # 创建 socket 对象service_socket.setso…...

opencv 中如何通过欧式距离估算实际距离(厘米)
1:这个方法个人测试觉得是正确的,误差较小,目前满足我当前的需求,如果方法不对,请大家评论,完善。 2:确保拍摄的参照物是垂直的,如果不垂直,就会有误差,不垂…...

Flask+Layui开发案例教程
基于 Python 语言的敏捷开发框架_DjangoAdmin敏捷开发框架FlaskLayui版本_开发文档 软件产品基于 Python 语言,采用 Flask2.x、Layui、MySQL 等技术栈精心打造的一款集模块化、高性能、组件化于一体的企业级敏捷开发框架,本着简化开发、提升开发效率的初…...

复现ORB3-YOLO8项目记录
文章目录 1.编译错误1.1 错误11.2 错误21.3 错误31.4 错误4 1.编译错误 首先ORB-SLAM相关项目已经写过很多篇博客了,从ORB-SLAM2怎么运行,再到现在的项目。关于环境已经不想多说了 1.1 错误1 – DEPENDENCY_LIBS : /home/lvslam/ORB3-YOLO8/Thirdparty…...

【jvm】字符串常量池问题
目录 一、基本概念1.1 说明1.2 特点 二、存放位置2.1 JDK1.6及以前2.2 JDK1.72.3 JDK1.8及以后 三、工作原理3.1 创建字符串常量3.2 使用new关键字创建字符串 四、intern()方法4.1 作用 五、优点六、字节码分析6.1 示例16.1.1 代码示例6.1.2 字节码6.1.3 解析 6.2 示例26.2.1 代…...
:I2C EEPROM实验)
STM32学习和实践笔记(39):I2C EEPROM实验
1.I2C总线介绍 I2C(Inter-Integrated Circuit)总线是由PHILIPS公司开发的两线式串行总线,用于连接微控制器及其外围设备,是微电子通信控制领域广泛采用的一种总线标准。 它是同步通信的一种特殊形式,具有接口线少,控制方式简单,器件封装形式小,通信速率较高等优点。I…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...
