人工智能算法工程师(中级)课程4-sklearn机器学习之回归问题与代码详解
大家好,我是微学AI,今天给大家介绍一下人工智能算法工程师(中级)课程4-sklearn机器学习之回归问题与代码详解。回归分析是统计学和机器学习中的一种重要方法,用于研究因变量和自变量之间的关系。在机器学习中,回归算法被广泛应用于预测分析、趋势分析等领域。本文将介绍sklearn机器学习库中的一些常用回归算法,包括线性回归、Lasso回归、岭回归、多任务岭回归、核岭回归以及SVM-SVR模型。我们将分别介绍这些算法的数学原理和公式,并配套完整可运行代码。
文章目录
- sklearn机器学习中的回归介绍与代码详解
- 1. 线性回归
- 线性回归的数学原理
- 线性回归的代码实现
- 2. Lasso回归和岭回归
- Lasso回归和岭回归的数学原理
- Lasso回归和岭回归的代码实现
- 3. 多任务岭回归
- 多任务岭回归的数学原理
- 多任务岭回归的代码实现
- 4. 核岭回归
- 核岭回归的数学原理
- 核岭回归的代码实现
- 5. SVM-SVR模型
- SVM-SVR模型的数学原理
- SVM-SVR模型的代码实现
- 总结

sklearn机器学习中的回归介绍与代码详解
1. 线性回归
线性回归是最简单的回归算法,它假设因变量和自变量之间存在线性关系。线性回归的目标是找到一条直线,使得所有数据点到这条直线的距离之和最小。这个目标可以通过最小二乘法来实现。
线性回归的数学原理
线性回归的模型可以表示为:
y = β 0 + β 1 x 1 + β 2 x 2 + ⋯ + β n x n + ε y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \cdots + \beta_nx_n + \varepsilon y=β0+β1x1+β2x2+⋯+βnxn+ε
其中, y y y是因变量, x 1 , x 2 , … , x n x_1, x_2, \ldots, x_n x1,x2,…,xn是自变量, β 0 , β 1 , … , β n \beta_0, \beta_1, \ldots, \beta_n β0,β1,…,βn是模型参数, ε \varepsilon ε是误差项。
最小二乘法的目标是最小化误差平方和:
J ( β ) = ∑ i = 1 m ( y i − y ^ i ) 2 = ∑ i = 1 m ( y i − ( β 0 + β 1 x i 1 + β 2 x i 2 + ⋯ + β n x i n ) ) 2 J(\beta) = \sum_{i=1}^{m}(y_i - \hat{y}_i)^2 = \sum_{i=1}^{m}(y_i - (\beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + \cdots + \beta_nx_{in}))^2 J(β)=i=1∑m(yi−y^i)2=i=1∑m(yi−(β0+β1xi1+β2xi2+⋯+βnxin))2
其中, m m m是样本数量, y i y_i yi是第 i i i个样本的因变量值, y ^ i \hat{y}_i y^i是第 i i i个样本的预测值。
线性回归的代码实现
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import numpy as np
# 生成模拟数据
np.random.seed(0)
X = np.random.rand(100, 1)
y = 2 * X[:, 0] + 1 + np.random.randn(100) * 0.05
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# 创建线性回归模型
model = LinearRegression()
# 训练模型
model.fit(X_train, y_train)
# 预测
y_pred = model.predict(X_test)
# 评估模型
mse = mean_squared_error(y_test, y_pred)
print("Mean squared error: ", mse)
2. Lasso回归和岭回归
Lasso回归和岭回归是两种常用的正则化线性回归算法。它们在普通线性回归的基础上加入了正则化项,以避免过拟合问题。
Lasso回归和岭回归的数学原理
Lasso回归的模型可以表示为:
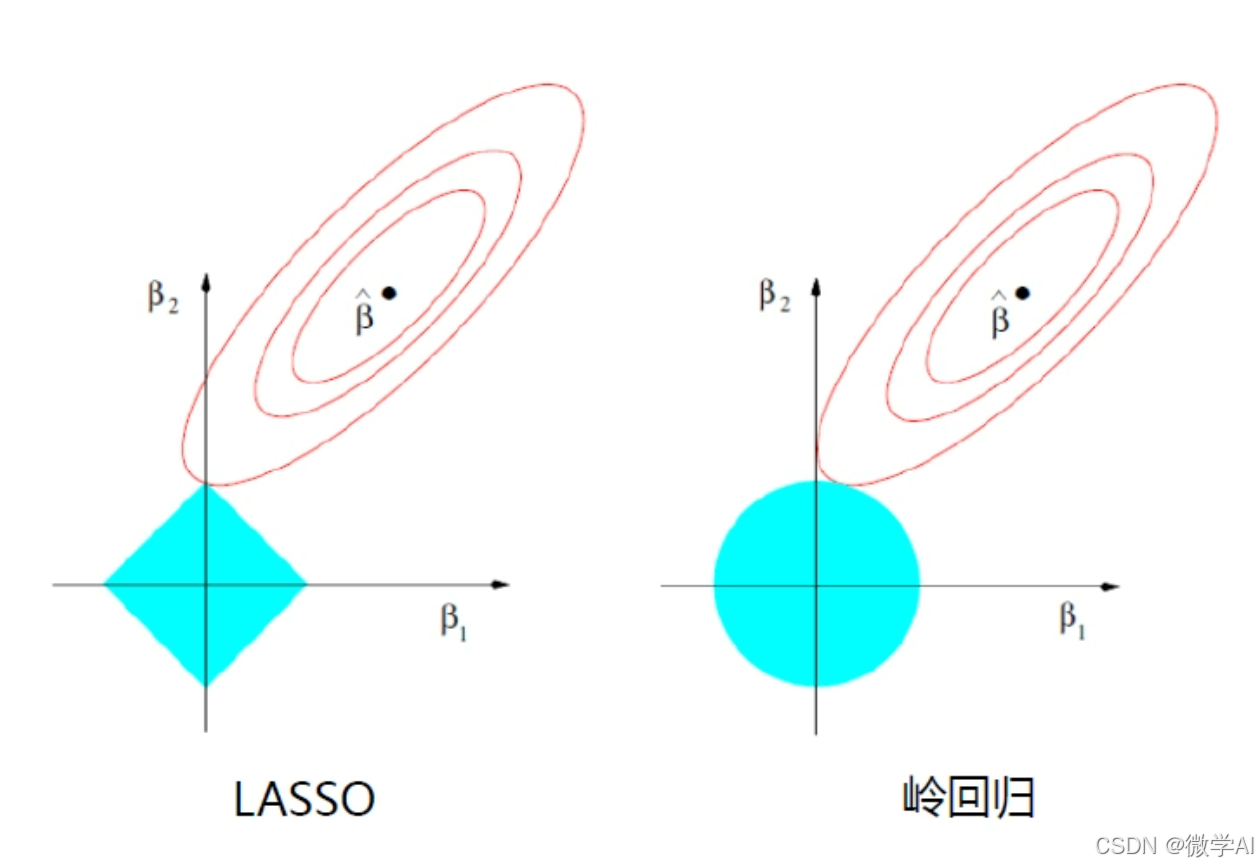
J ( β ) = ∑ i = 1 m ( y i − ( β 0 + β 1 x i 1 + β 2 x i 2 + ⋯ + β n x i n ) ) 2 + α ∑ j = 1 n ∣ β j ∣ J(\beta) = \sum_{i=1}^{m}(y_i - (\beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + \cdots + \beta_nx_{in}))^2 + \alpha \sum_{j=1}^{n}|\beta_j| J(β)=i=1∑m(yi−(β0+β1xi1+β2xi2+⋯+βnxin))2+αj=1∑n∣βj∣
岭回归的模型可以表示为:
J ( β ) = ∑ i = 1 m ( y i − ( β 0 + β 1 x i 1 + β 2 x i 2 + ⋯ + β n x i n ) ) 2 + α ∑ j = 1 n β j 2 J(\beta) = \sum_{i=1}^{m}(y_i - (\beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + \cdots + \beta_nx_{in}))^2 + \alpha \sum_{j=1}^{n}\beta_j^2 J(β)=i=1∑m(yi−(β0+β1xi1+β2xi2+⋯+βnxin))2+αj=1∑nβj2
其中, α \alpha α是正则化参数。
Lasso回归和岭回归的代码实现
from sklearn.linear_model import Lasso, Ridge
# 创建Lasso回归模型
lasso_model = Lasso(alpha=0.1)
# 创建岭回归模型
ridge_model = Ridge(alpha=0.1)
# 训练模型
lasso_model.fit(X_train, y_train)
ridge_model.fit(X_train, y_train)
# 预测
lasso_pred = lasso_model.predict(X_test)
ridge_pred = ridge_model.predict(X_test)
# 评估模型
lasso_mse = mean_squared_error(y_test, lasso_pred)
ridge_mse = mean_squared_error(y_test, ridge_pred)
print("Lasso mean squared error: ", lasso_mse)
print("Ridge mean squared error: ", ridge_mse)
3. 多任务岭回归
多任务岭回归是岭回归的扩展,用于同时解决多个回归问题。这些问题通常是相关的,因此共享相同的特征空间,但有不同的目标值。
多任务岭回归的数学原理
多任务岭回归的目标是最小化以下目标函数:
J ( B ) = 1 2 n ∑ i = 1 n ∥ y i − X i B ∥ 2 2 + α 2 ∑ j = 1 k ∥ B j ∥ 2 2 J(\mathbf{B}) = \frac{1}{2n} \sum_{i=1}^{n} \left\| \mathbf{y}_i - \mathbf{X}_i \mathbf{B} \right\|^2_2 + \frac{\alpha}{2} \sum_{j=1}^{k} \left\| \mathbf{B}_j \right\|^2_2 J(B)=2n1i=1∑n∥yi−XiB∥22+2αj=1∑k∥Bj∥22
其中, B \mathbf{B} B是一个 p × k p \times k p×k的系数矩阵, p p p是特征数量, k k k是任务数量, y i \mathbf{y}_i yi是第 i i i个任务的因变量向量, X i \mathbf{X}_i Xi是第 i i i个任务的自变量矩阵, α \alpha α是正则化参数。
多任务岭回归的代码实现
from sklearn.linear_model import MultiTaskLasso
# 假设我们有两个任务回归任务
X = np.random.rand(100, 10)
y = np.random.rand(100, 2)
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# 创建多任务岭回归模型
multi_task_lasso = MultiTaskLasso(alpha=0.1)
# 训练模型
multi_task_lasso.fit(X_train, y_train)
# 预测
multi_task_pred = multi_task_lasso.predict(X_test)
# 评估模型
multi_task_mse = mean_squared_error(y_test, multi_task_pred)
print("Multi Task Lasso mean squared error: ", multi_task_mse)
4. 核岭回归
核岭回归是非线性回归方法,它使用核技巧将数据映射到高维空间,然后维空间中进行线性回归。
核岭回归的数学原理
核岭回归的目标函数为表示为:
J ( w ) = 1 2 n ∥ K w − y ∥ 2 2 + α 2 w T w J(\mathbf{w}) = \frac{1}{2n} \left\| \mathbf{K} \mathbf{w} - \mathbf{y} \right\|^2_2 + \frac{\alpha}{2} \mathbf{w}^T \mathbf{w} J(w)=2n1∥Kw−y∥22+2αwTw
其中, K \mathbf{K} K是核矩阵, w \mathbf{w} w是权重向量, y \mathbf{y} y是因变量向量, α \alpha α是正则化参数。
核岭回归的代码实现
from sklearn.kernel_ridge import KernelRidge
# 创建核岭回归模型
kernel_ridge = KernelRidge(kernel='rbf', alpha=1.0)
# 训练模型
kernel_ridge.fit(X_train, y_train.ravel())
# 预测
kernel_ridge_pred = kernel_ridge.predict(X_test)
# 评估模型
kernel_ridge_mse = mean_squared_error(y_test, kernel_ridge_pred)
print("Kernel Ridge mean squared error: ", kernel_ridge_mse)
5. SVM-SVR模型
支持向量回归(SVR)是支持向量机(SVM)在回归问题上的应用。SVR的目标是找到一个最优的超平面,使得所有数据点到这个超平面的距离之和最小。
SVM-SVR模型的数学原理
SVR的目标函数可以表示为:
min w , b , ξ , ξ ∗ 1 2 ∥ w ∥ 2 + C ∑ i = 1 n ( ξ i + ξ i ∗ ) \min_{\mathbf{w}, b, \xi, \xi^*} \frac{1}{2} \left\| \mathbf{w} \right\|^2 + C \sum_{i=1}^{n} (\xi_i + \xi_i^*) w,b,ξ,ξ∗min21∥w∥2+Ci=1∑n(ξi+ξi∗)
约束条件为:
y i − w T ϕ ( x i ) − b ≤ ε + ξ i w T ϕ ( x i ) + b − y i ≤ ε + ξ i ∗ ξ i , ξ i ∗ ≥ 0 \begin{align*} y_i - \mathbf{w}^T \phi(\mathbf{x}_i) - b &\leq \varepsilon + \xi_i \\ \mathbf{w}^T \phi(\mathbf{x}_i) + b - y_i &\leq \varepsilon + \xi_i^* \\ \xi_i, \xi_i^* &\geq 0 \end{align*} yi−wTϕ(xi)−bwTϕ(xi)+b−yiξi,ξi∗≤ε+ξi≤ε+ξi∗≥0
其中, w \mathbf{w} w是权重向量, b b b是偏置项, ϕ ( x i ) \phi(\mathbf{x}_i) ϕ(xi)是将输入向量映射到高维空间的函数, ξ \xi ξ和 ξ ∗ \xi^* ξ∗是松弛变量, C C C是惩罚参数, ε \varepsilon ε是容忍误差。
SVM-SVR模型的代码实现
from sklearn.svm import SVR
# 创建SVR模型
svr = SVR(kernel='rbf', C=1.0, epsilon=0.1)
# 训练模型
svr.fit(X_train, y_train.ravel())
# 预测
svr_pred = svr.predict(X_test)
# 评估模型
svr_mse = mean_squared_error(y_test, svr_pred)
print("SVR mean squared error: ", svr_mse)
总结
本文给大家展示了线性回归、Lasso回归、岭回归、多任务岭回归、核岭回归以及SVM-SVR模型在sklearn库中的实现。每个模型都包括了模型的创建、训练、预测和评估过程。在实际应用中,您需要根据具体问题选择合适的模型,并通过调整模型参数来优化模型性能。
sklearn库为各种回归算法提供了方便的接口,使得在Python中进行回归分析变得简单高效。通过理解和实践这些算法,您可以更好地解决实际问题,并在机器学习领域取得更好的成果。
相关文章:

人工智能算法工程师(中级)课程4-sklearn机器学习之回归问题与代码详解
大家好,我是微学AI,今天给大家介绍一下人工智能算法工程师(中级)课程4-sklearn机器学习之回归问题与代码详解。回归分析是统计学和机器学习中的一种重要方法,用于研究因变量和自变量之间的关系。在机器学习中,回归算法被广泛应用于…...

智能制造热点词汇科普篇——工业微服务
随着互联网技术的不断发展,近十年来,微服务也逐渐走进人们的视线中来。何为微服务?让我们先来看看百度百科上的定义:微服务(或称微服务架构)是一种云原生架构方法,在单个应用中包含众多松散耦合…...
FastGPT+OneAI接入网络模型
文章目录 FastGPT连接OneAI接入网络模型1.准备工作2.开始部署2.1下载 docker-compose.yml2.2修改docker-compose.yml里的参数 3.打开FastGPT添加模型3.1打开OneAPI3.2接入网络模型3.3重启服务 FastGPT连接OneAI接入网络模型 1.准备工作 本文档参考FastGPT的官方文档 主机ip接…...
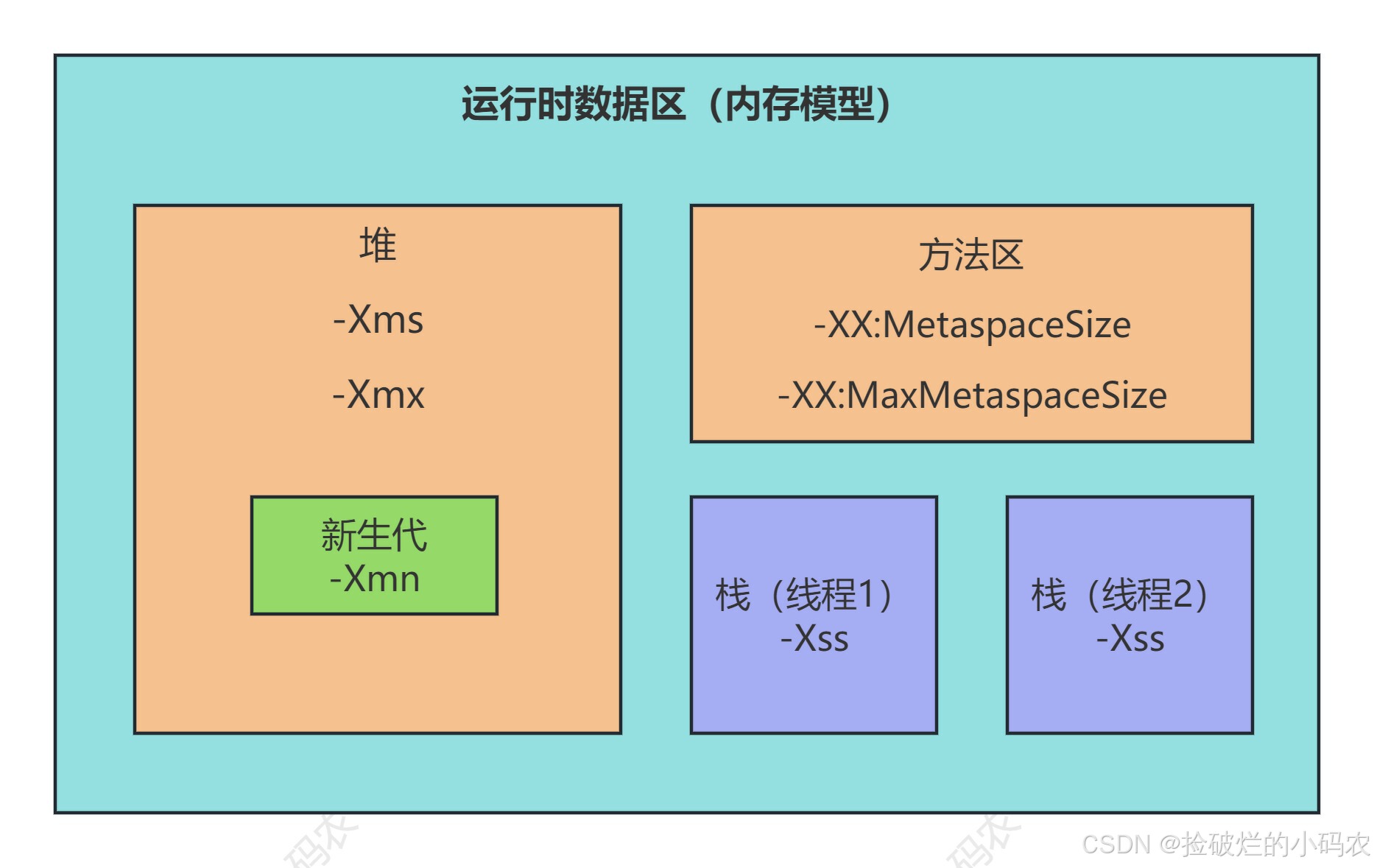
Java核心篇之JVM探秘:内存模型与管理初探
系列文章目录 第一章 Java核心篇之JVM探秘:内存模型与管理初探 第二章 Java核心篇之JVM探秘:对象创建与内存分配机制 第三章 Java核心篇之JVM探秘:垃圾回收算法与垃圾收集器 第四章 Java核心篇之JVM调优实战:Arthas工具使用及…...

未来互联网的新篇章:深度解析Facebook的技术与战略
随着科技的飞速发展和社会的不断变迁,互联网作为全球信息交流的重要平台,正经历着前所未有的变革和演进。作为全球最大的社交媒体平台之一,Facebook不仅是人们沟通、分享和互动的重要场所,更是科技创新和数字化进程的推动者。本文…...
MySQL卸载 - Windows版
MySQL卸载 - Windows版 1. 停止MySQL服务 winR 打开运行,输入 services.msc 点击 “确定” 调出系统服务。 2. 卸载MySQL相关组件 打开控制面板 —> 卸载程序 —> 卸载MySQL相关所有组件 3. 删除MySQL安装目录 4. 删除MySQL数据目录 数据存放目录是在 …...
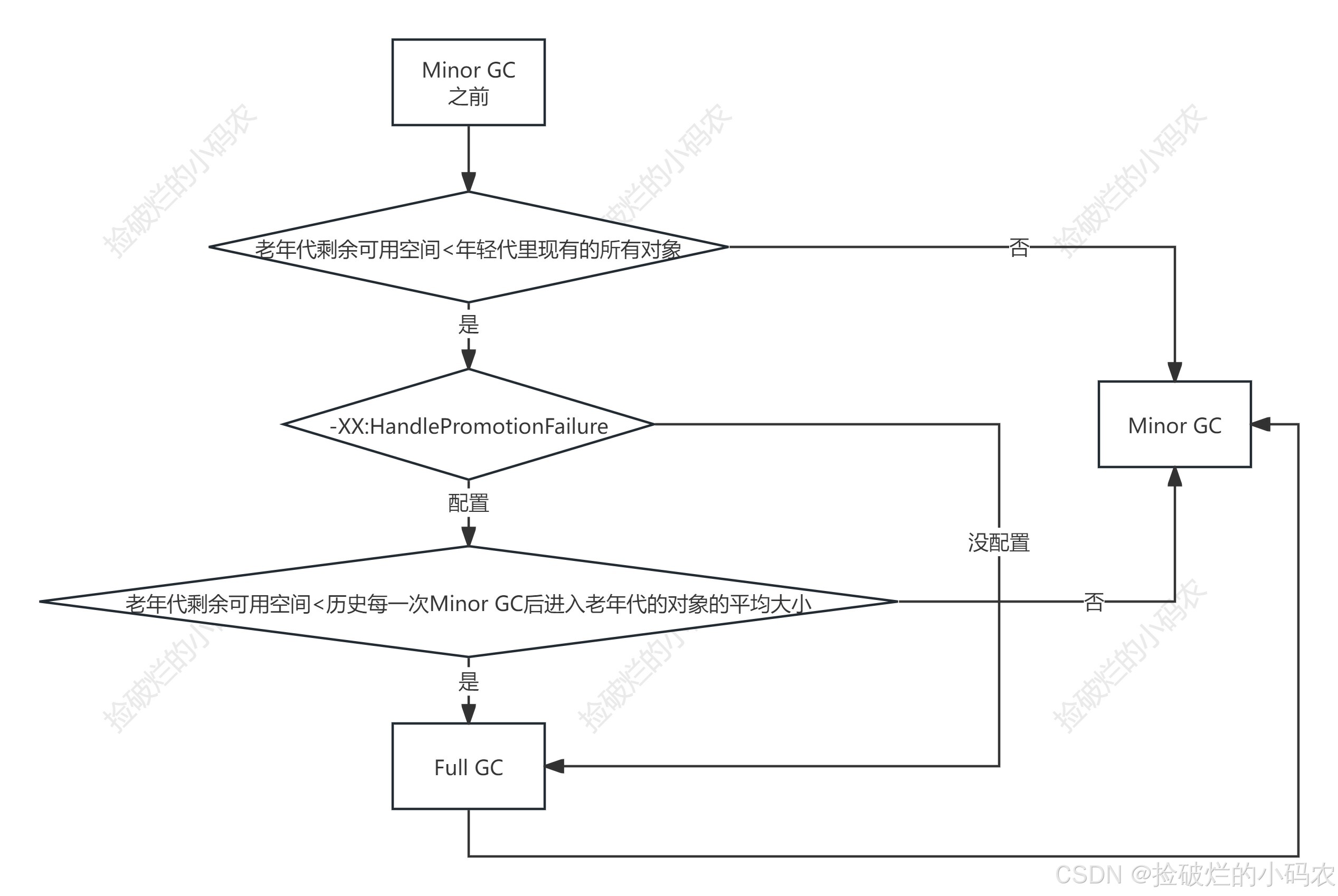
Java核心篇之JVM探秘:对象创建与内存分配机制
系列文章目录 第一章 Java核心篇之JVM探秘:内存模型与管理初探 第二章 Java核心篇之JVM探秘:对象创建与内存分配机制 第三章 Java核心篇之JVM探秘:垃圾回收算法与垃圾收集器 第四章 Java核心篇之JVM调优实战:Arthas工具使用及…...

Nuxt框架中内置组件详解及使用指南(五)
title: Nuxt框架中内置组件详解及使用指南(五) date: 2024/7/10 updated: 2024/7/10 author: cmdragon excerpt: 摘要:本文详细介绍了Nuxt框架中和组件的使用方法与配置,包括安装、基本用法、属性详解、示例代码以及高级功能如…...
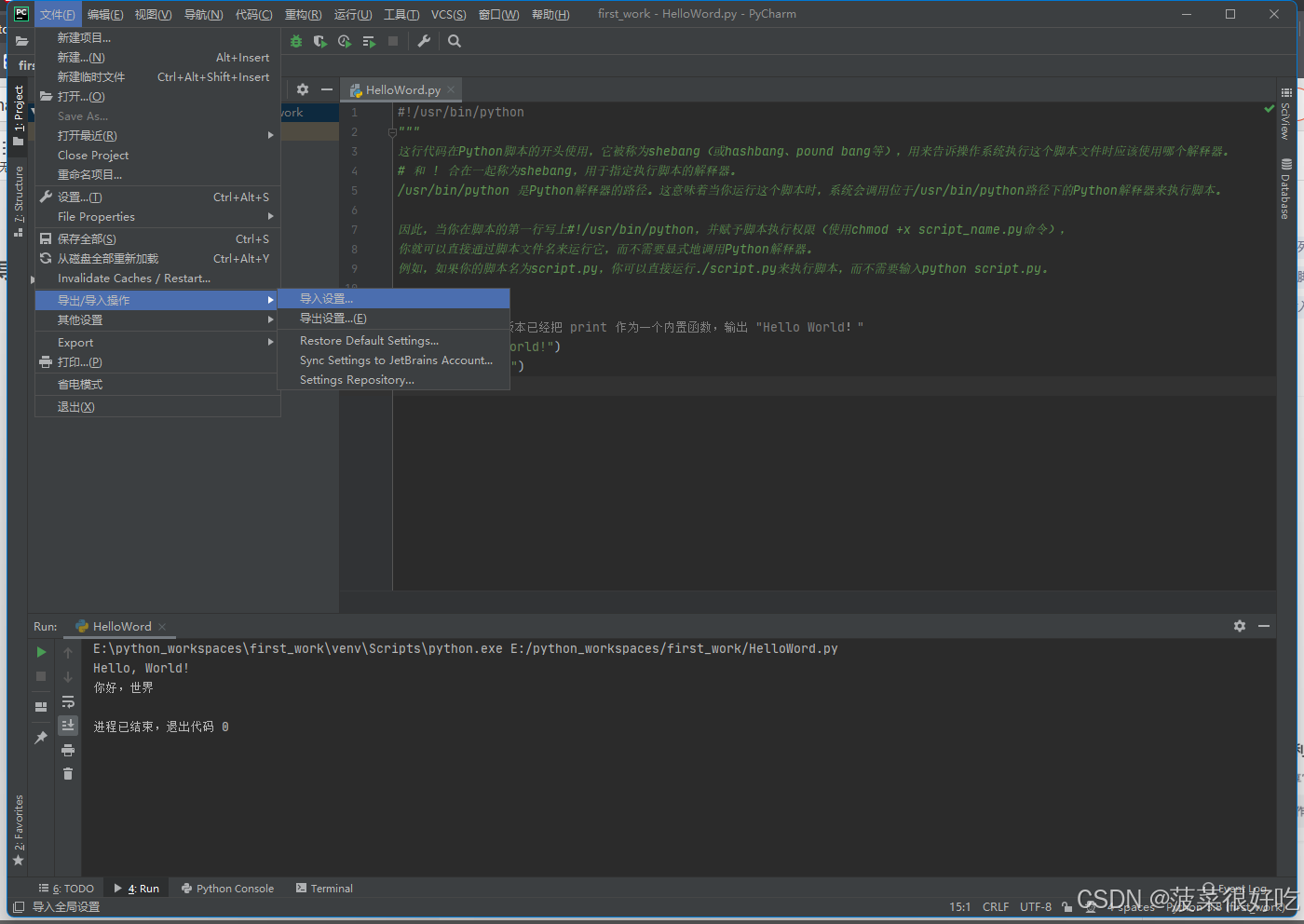
python开发遇到的坑汇总
文章目录 1.点击导入操作,所有配置全没了 1.点击导入操作,所有配置全没了 在 PyCharm 中,如果你遇到了点击导入(import)操作后,项目似乎进行了重新安装或重新部署的情况,这通常不是由简单的导入…...
【线性表,线性表中的顺序表和链表】
目录 1、线性表的定义和基本操作1.1、线性表的定义1.2、线性表的基本操作 2、顺序表和链表的比较2.1、顺序表2.1.1、顺序表的定义和特点2.1.2、顺序表的实现(1)顺序表的静态分配:(2)顺序表的动态分配 2.1.3、顺序表的基…...

46 mysql 客户端拿不到具体的错误信息
前言 这是最近碰到的一个问题 同样的一个 环境的问题, 在正常的 mysql 环境会返回 具体的错误信息, 然后 在我的另外一个环境里面 只能返回一些 unknown error 之类的 十分抽象的环境 然后 我们这里 来看一下 具体的情况 我们这里从 错误的环境 往前推导 来查看 并解决这个…...

Java语言程序设计——篇三(2)
循环结构 概述1️⃣while循环例题讲解 2️⃣do-while循环例题讲解 🚩while循环与do-while循环区别3️⃣for循环例题讲解 4️⃣循环的嵌套🏮例题讲解 概述 ⭐️Java语言提供了4种循环结构: (1) while循环 (2) do-while循环 (3) for循环 (4)增…...

如何实现一个分布式锁
如何实现一个分布式锁 本篇内容主要介绍如何使用 Java 语言实现一个注解式的分布式锁,主要是通过注解AOP 环绕通知来实现。 1. 锁注解 我们首先写一个锁的注解 /*** 分布式锁注解*/ Retention(RetentionPolicy.RUNTIME) Target({ElementType.METHOD}) Documente…...

Ajax从零到实战
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 非常期待和您一起在这个小…...

编程参考 - 在C++移动构造函数声明中使用noexcept
在 C 中,noexcept 是用于表示函数不抛出异常的指定符。它既可用于常规函数,也可用于特殊成员函数,包括构造函数和析构函数。使用 noexcept 可以帮助编译器进行优化,提高代码的安全性和正确性。 In C, noexcept is a specifier use…...

Vue2/Vue3实现全局/局部添加防篡改水印的效果。删除元素无效!更改元素属性无效!支持图片、元素、视频等等。
水印目的 版权保护:水印可以在图片、文档或视频中嵌入作者、品牌或版权所有者的信息,以防止未经授权的复制、传播或使用。当其他人使用带有水印的内容时,可以追溯到原始作者或版权所有者,从而加强版权保护。 身份识别:水印可以用作作者或品牌的标识符,使观众能够轻松识…...
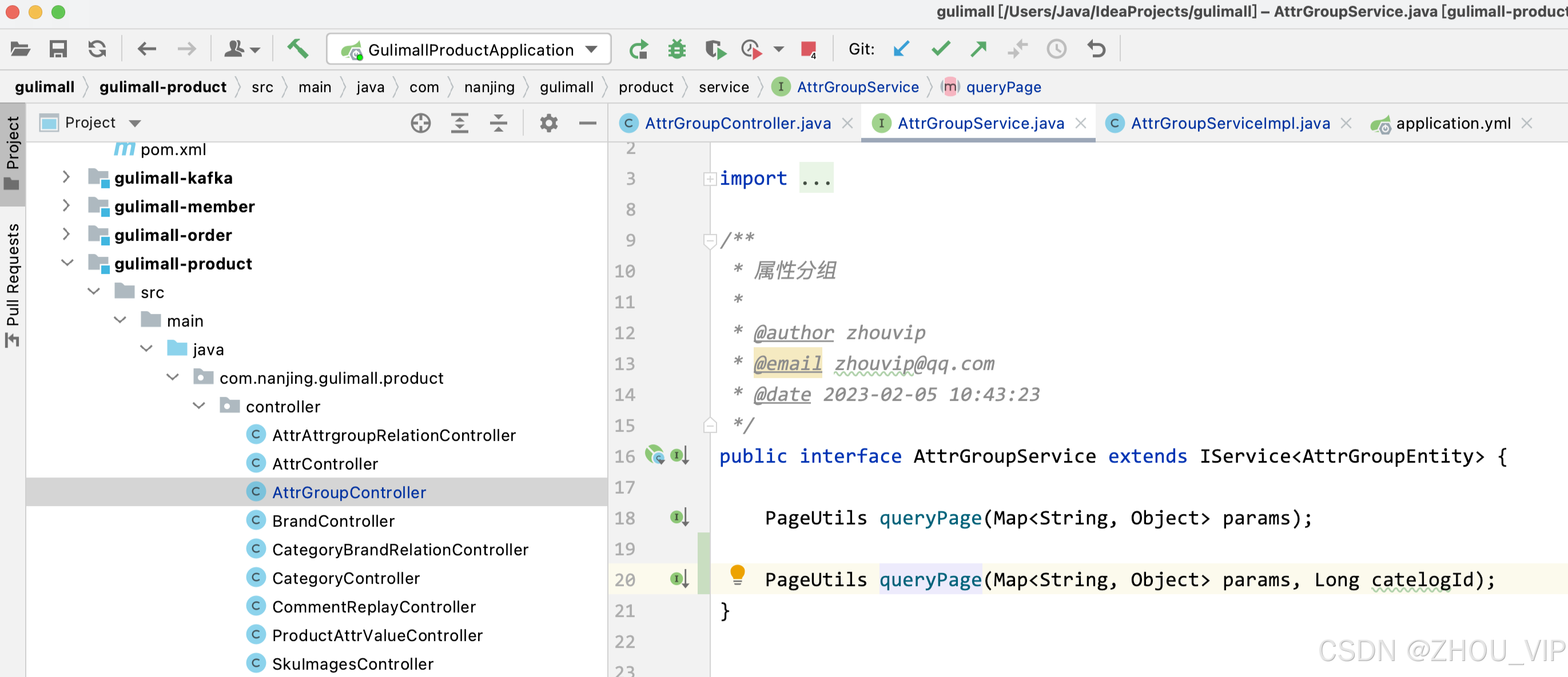
GuLi商城-商品服务-API-属性分组-获取分类属性分组
获取分类属性分组接口开发 操作的是这张表 造数据: 后台代码: @Override public PageUtils queryPage(Map<String, Object> params, Long catelogId) {//select * from pms_attr_group where catelog_id=? and (attr_group_id=key or attr_group_name like %key%)Stri…...
安全测试理论
安全测试理论 什么是安全测试? 安全测试:发现系统安全隐患的过程安全测试与传统测试区别 传统测试:发现bug为目的 安全测试:发现系统安全隐患什么是渗透测试 渗透测试:已成功入侵系统为目标的的攻击过程渗透测试与安全…...

序列化和反序列化
面试题:对序列化和反序列化的理解? 我们之所以需要序列化,它核心的目的是为了解决网络通信之间的对象传输的问题,也就是说,如何把当前JVM进程的一个对象,通过跨网络传输到另一个JVM进程里面,而序…...

OpenCV中使用Canny算法在图像中查找边缘
操作系统:ubuntu22.04OpenCV版本:OpenCV4.9IDE:Visual Studio Code编程语言:C11 算法描述 Canny算法是一种广泛应用于计算机视觉和图像处理领域中的边缘检测算法。它由John F. Canny在1986年提出,旨在寻找给定噪声条件下的最佳边…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
