【基础算法】单链表的OJ练习(5) # 环形链表 # 环形链表II # 对环形链表II的解法给出证明(面试常问到)
文章目录
- 前言
- 环形链表
- 环形链表 II
- 写在最后
前言
-
本章的
OJ练习相对于OJ练习(4)较为简单。不过,本章的OJ最重要的是要我们证明为何可以这么做。这也是面试中常出现的。 -
对于
OJ练习(4):-> 传送门 <-,分割链表以一种类似于归并的思想解得,回文链表以一种巧妙复用前面OJ题的思想解得。 -
啰嗦一下:对于本章,最重要的是需要证明为什么这样做可以,所以我们不光要做出来
OJ,还要能够理解并自行给出证明。
环形链表
-
题目链接: -> 传送门 <-。
-
题目描述:给你一个链表的头节点
head,判断链表中是否有环。如果链表中存在环 ,则返回true。 否则,返回false。
带环链表类似于下面这种结构:
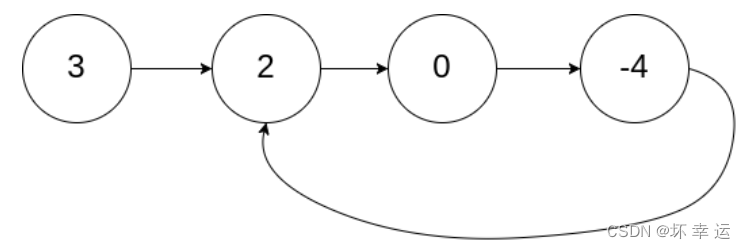
- 是否有环,实际上就是链表的最后一个节点是否指向了链表其中的一个节点,如果有环,我们遍历一遍链表的话,会陷入死循环。那么我们该如何判断链表是否有环呢?
解题思路:
-
由于带环链表直接遍历会陷入死循环,也就是说会无限在环内遍历下去,因此,这里可以引出一个追击问题:用快慢指针遍历链表。
-
我们定义两个指针,分别是慢指针
slow,快指针fast,这两个指针同时遍历链表,slow每次走一步,fast每次走两步。fast会先进入环然后在环内跑圈,当slow进入环后,这就是一个典型的追及问题了,slow每次在环内走一步,fast每次在环内走两步,两个指针的距离每次缩小1,最终fast会追上slow与slow指向同一节点。当两个指针相等时,就可以判断该链表带环,因此判断条件就是fast == slow (return true)。 -
如果链表不带环,
fast最终会指向NULL的前一个结点或者就指向NULL。因此,整个判断过程就结束了。


- 可以看到,如果链表没有环,链表的结点个数为偶数时,
fast是指向NULL结束,链表的节点个数为奇数时,fast是指向最后一个结点结束。
解题代码:
bool hasCycle(struct ListNode *head) {struct ListNode* fast = head, * slow = head;while (fast && fast->next){fast = fast->next->next;slow = slow->next;if (fast == slow) return true;}return false;
}
为什么快慢指针可以?
-
快指针每次走两步,慢指针每次走一步,当两个指针都在环内的时候,就成了一个追击问题,两个指针的距离每次缩小一,最终快指针会追上慢指针,因此判断其有环。
-
那假如快指针每次走三步,慢指针走一步呢?
我们将带环链表抽象成下图:

假设每次快指针走三步,慢指针每次走一步,当两个指针都进环后,此时的相对位置为:
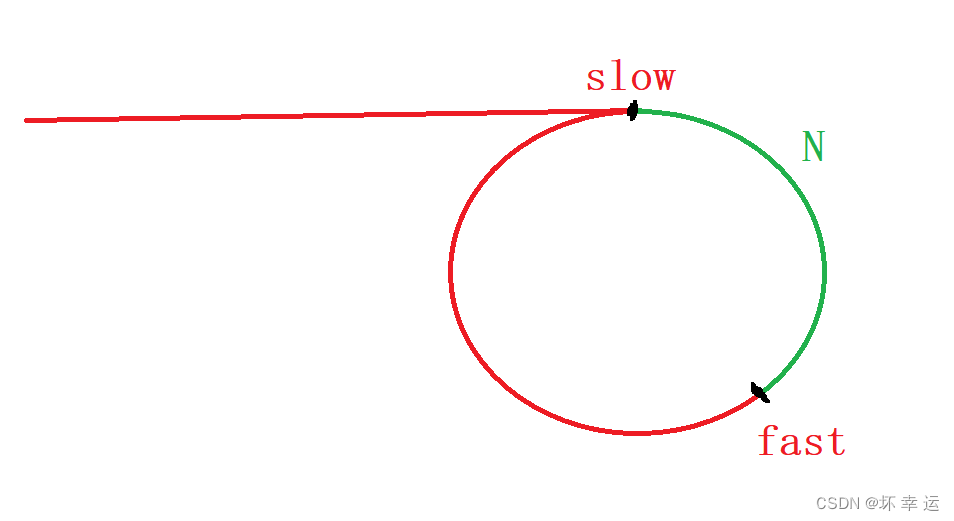
我们记此时慢指针slow与快指针fast的距离为N,慢指针每次走一步,快指针每次走三步,因此N每次减少2,于是就有:
N - 2
N - 4
N - 6
N - 8
.....
最终有两种情况:
😃.N = 1,然后再减2 -> -1
😉.N = 2,然后再减2 -> 0
-
如果N最后减为
-1,那么再次追击,如果N最后减为0,则快指针等于慢指针,判断为true。所以得出:当N为奇数时,追不上;当N为偶数时,一定追得上。 -
如果追不上,最后
fast会在slow的下一个位置,然后继续追击,那么,继续追击又是否追的上呢?
我们假设环的长度为C,那么此时再次追击两个指针的距离就为:C - 1,令T = C - 1,则:
T - 2
T - 4
T - 6
T - 8
.....
最终有两种情况:
😃.T = 1,然后再减2 -> -1
😉.T = 2,然后再减2 -> 0
- 因此,这里又有两种情况,有了前面的推导,这里不难得出,当
C为偶数时,则C - 1(T)为奇数,此时继续追不上,并且下一次也是一样,所以这里会陷入死循环;当C为奇数时,则C - 1为偶数,此时是追的上的。因此,当C为偶数时,永远追不上,当C为奇数时,追的上。
所以,通过以上分析,快指针每次走三步,慢指针每次走一步不一定能判断是否为带环链表,可能会陷入死循环,尽管陷入死循环就说明带环。
那么快指针每次走
4步,走5步,走n步呢?这里就不是我们该探讨的范围了,相信大家心里已经有答案了。
环形链表 II
-
题目链接:-> 传送门 <-。
-
题目描述:给定一个链表的头节点
head,返回链表开始入环的第一个节点。 如果链表无环,则返回null。注意:不允许修改链表。 -
与上一题不同的是,这一题首先是要判断链表是否带环,然后在带环的基础上返回链表入环的第一个节点。类似于下图:
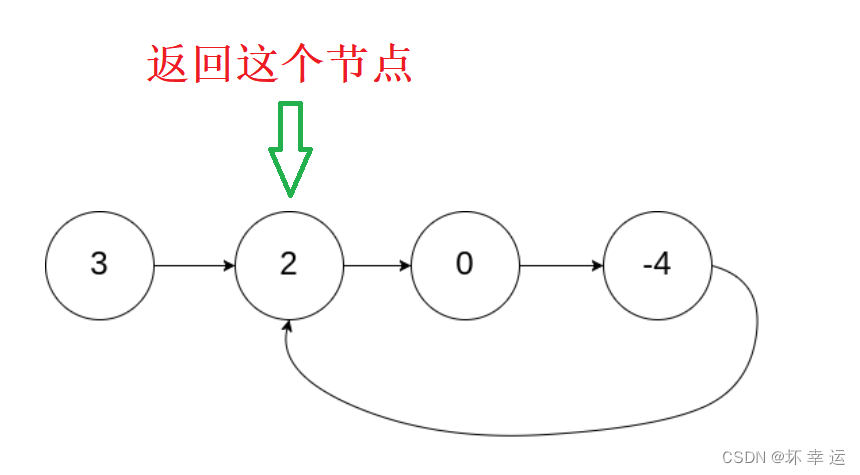
解题思路:
- 这里直接说做法:先以第一题的思路使用快慢指针找到快指针和慢指针相遇的那个点,然后一个指针从该点开始走,一个指针从头开始走,每次走一步,最终两个指针会在入环的第一个节点相遇,然后返回这个节点。
解题代码:
struct ListNode *detectCycle(struct ListNode *head) {struct ListNode *slow = head, *fast = head;while (fast && fast->next){// 快指针每次走两步fast = fast->next->next;// 慢指针每次走一步slow = slow->next;// 如果找到相遇的那个点,就开始找入环的第一个节点if (slow == fast){struct ListNode *cur = slow;// 一个从头开始走,一个从当前节点开始走while (cur != head){head = head->next;cur = cur->next;}// 最终相遇的那个点就是入环的第一个节点return cur;}}// 如果链表不带环,就返回NULLreturn NULL;
}
证明:为什么一个指针从快慢指针相遇的那个点开始走,一个指针从头开始走,最终两个指针会在入环的第一个节点处相遇?
- 假设快慢指针在
pos位置相遇,设链表头到入环的第一个节点的距离为X, 入环的第一个节点到pos的距离为Y,pos到入环的第一个节点的距离为L,整个环的周长为C:
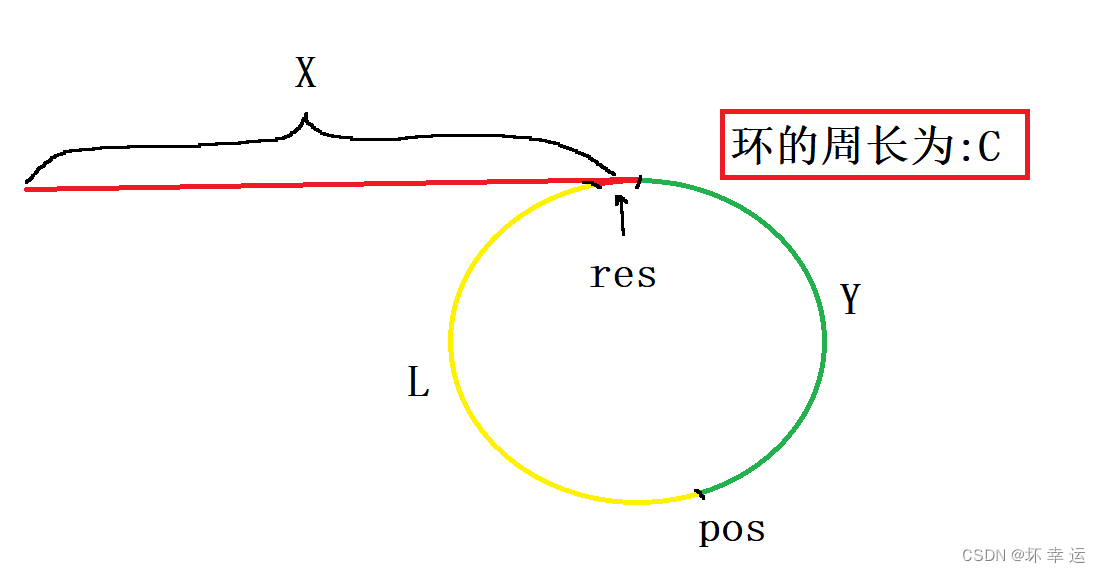
由此,我们计算一下,当快慢指针在pos相遇时分别走了多长的距离:
😃 快指针:X + nC + Y;
😉 慢指针:X + Y;
😮 为什么快指针有个
nC而不是C?
😮 为什么慢指针没有C?
- 快指针有个
nC是因为:有可能这个环的长度比较短,在慢指针入环时,快指针已经在环内走了n圈了。 - 慢指针没有
C是因为:慢指针入环后最多只会走C - 1步,不可能出现在环内步数超过一圈的情况,因此慢指针没有C。
因此由快指针每次走两步,慢指针每次走一步的特点可以得出下面这个公式:
X + nC + Y = 2(X + Y);
化简得:
X = nC - Y;
进一步化简得:
X = (n - 1)C + (C - Y);
最终得:
X = (n - 1)C + L;
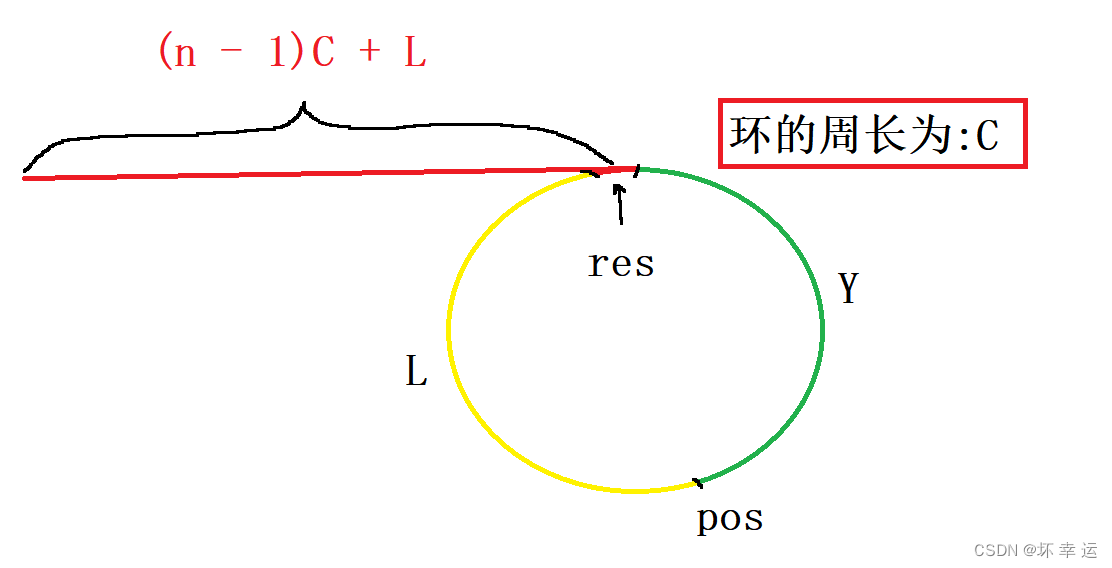
由此公式,当一个指针从pos开始走,他走了(n - 1)C,最终还是会在pos位置。而当(n - 1)C走完后,从头开始走的指针与入环的第一个节点的距离为L,与此时pos到入环的第一个节点的距离相等。因此,为什么这样的做法可以,以上就是答案。
写在最后
对于单链表的题目练习,最重要的是思路,我们在数据结构阶段要养成画图的习惯,因为它能帮助我们更好的理解。后续还会有单链表相关的题目练习。
感谢阅读本小白的博客,错误的地方请严厉指出噢!
相关文章:

【基础算法】单链表的OJ练习(5) # 环形链表 # 环形链表II # 对环形链表II的解法给出证明(面试常问到)
文章目录前言环形链表环形链表 II写在最后前言 本章的OJ练习相对于OJ练习(4)较为简单。不过,本章的OJ最重要的是要我们证明为何可以这么做。这也是面试中常出现的。 对于OJ练习(4):-> 传送门 <-,分割链表以一种类似于归并的思想解得&a…...

MySQL 基础教程[13]
MySQL 基础教程[13]问题1问题1代码问题2问题2代码本系列MySQL 基础教程通过“问题-代码”的方式介绍各类方法,每篇设置2个MySQL综合问题,并给出解决方案。 问题1 kwgl数据库中有学生基本信息表student和系别表dept。表结构及说明如下: student (sid, s…...

个人练习-Leetcode-826. Most Profit Assigning Work
题目链接:https://leetcode.cn/problems/most-profit-assigning-work/ 题目大意:给出一串任务,difficulty表示任务难度,profit表示任务的收益(以下简称diff和pro)。给出一串工人的能力worker。每个工人只能…...

云原生周刊:边缘计算会吞噬云吗?| 2023.3.13
文章推荐 边缘计算吞噬云? 这篇文章讨论了边缘计算对传统云计算的潜在冲击。 边缘计算是一种新型的计算架构,它将计算移动到离数据源和终端设备更近的地方,从而提供更快的响应时间和更好的用户体验。相比之下,云计算是一种集中…...
python+django+vue图书个性化推荐系统
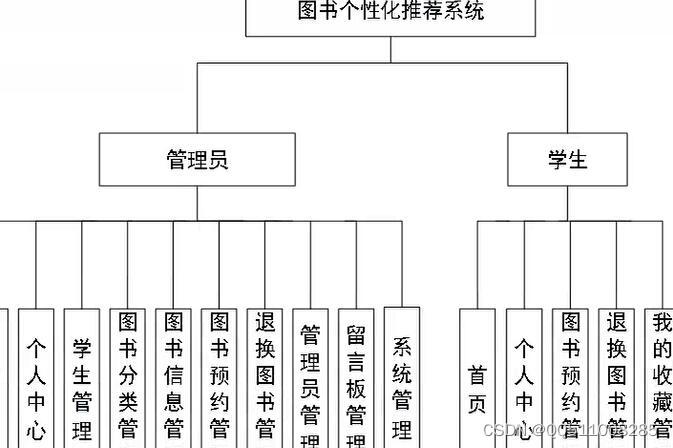
整个系统是由多个功能模块组合而成的,要将所有的功能模块都一一列举出来,然后进行逐个的功能设计,使得每一个模块都有相对应的功能设计,然后进行系统整体的设计。 本图书个性化推荐系统结构图如图python manage.py runserver 开…...
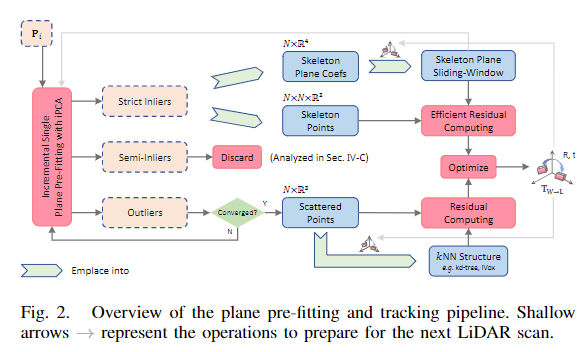
经典文献阅读之--LIO-PPF(增量平面预拟合LIO)
0. 简介 自从ikd-tree出来后,现在越来越多的工作瞄准了增量式这种方法,比如说激光惯导里程计(LIDAR-Inertial Odometry,LIO)的高精度跟踪通常涉及最小化点到平面距离的k最近邻(kNN)搜索&#x…...

ChatGPT背后有哪些关键技术?CSIG企业行带你一探究竟
目录1 ChatGPT的时代2 CSIG企业行3 议题&嘉宾介绍3.1 对生成式人工智能的思考3.2 对话式大型语言模型研究3.3 文档图像处理中的底层视觉技术4 观看入口1 ChatGPT的时代 2015年,马斯克、美国创业孵化器Y Combinator总裁阿尔特曼、全球在线支付平台PayPal联合创始…...
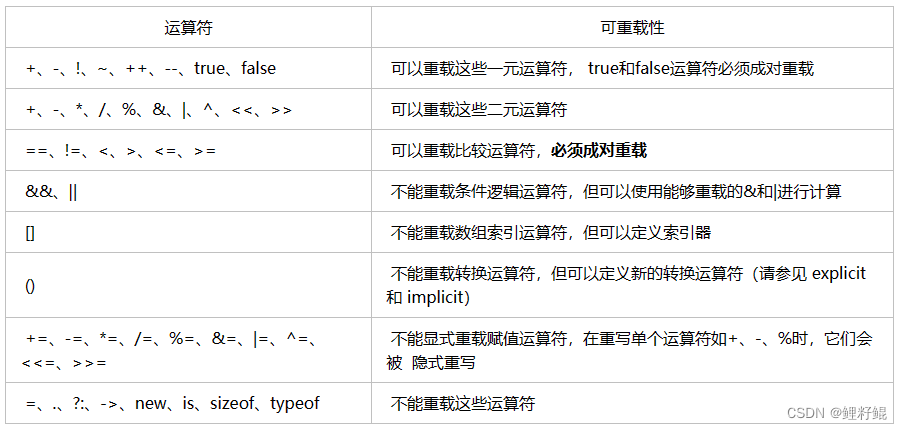
C#基础之面向对象编程(二)
总目录 文章目录总目录前言一、概述1. 定义2. 面向对象的三大特性二、封装1. 定义2. 属性三、继承1. 定义2. 继承的使用3. base 和this四、多态1. 定义2. 重写和重载3. 多态性的实现1、静态多态性2、动态多态性4. 向上转型和向下转型1、定义2、语法格式3、案例结语前言 本文主…...

蓝桥杯刷题冲刺 | 倒计时25天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录1.完全二叉树1.完全二叉树 题目 链接: 完全二叉树的权值 - 蓝桥云课 (lanqiao.cn) 给…...
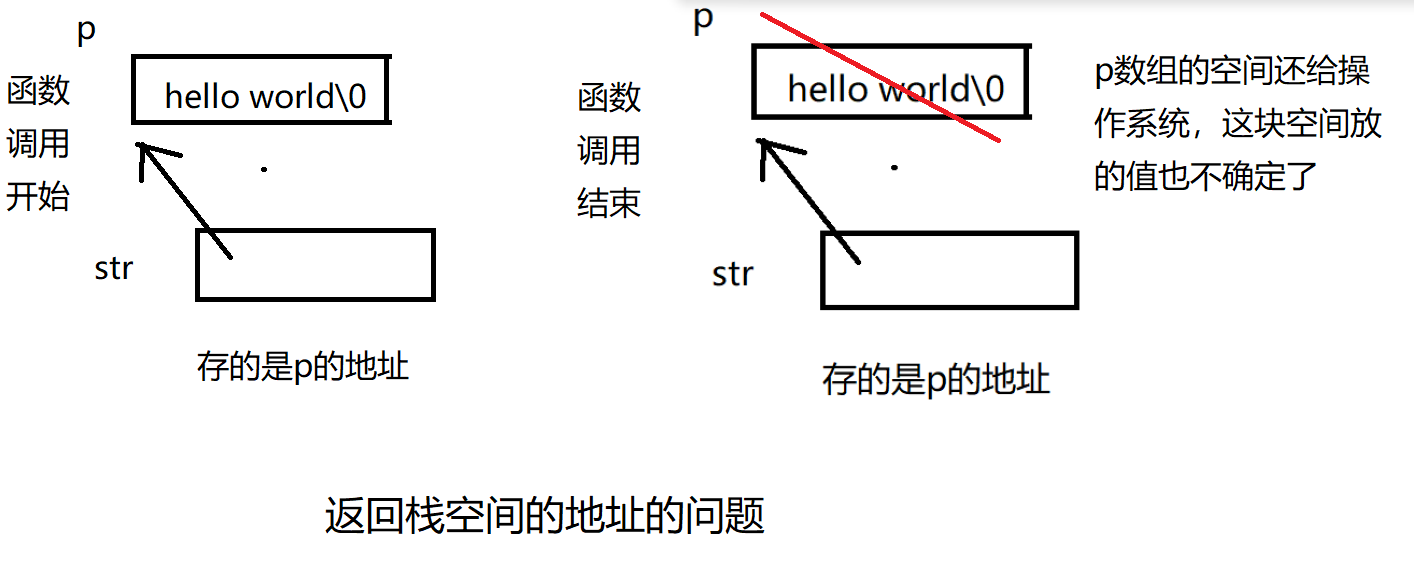
c语言—动态内存管理
一.为什么存在动态内存开辟开辟空间的特点:空间开辟大小是固定的数组在申明时,必须指定数组长度,她所需要的内存在编译时分配但是对于空间的需求,不仅仅是上述的情况。有时候我们需要的空间大小在程序运行的时候才能知道ÿ…...

请说明Ajax、Fetch、Axios三者的区别
相同点: 1、三者都用于网络请求,但是不同维度 2、 Ajax(Asynchronous Javascript and XML),一种技术的统称,并不是实际的API 3、Fetch是一个具体的API,浏览器里面直接有一个API就叫Fetch 4、 Axios是一个第三方库&…...

阿里p8测试总监,让我们用这份《测试用例规范》,再也没加班过
经常看到无论是刚入职场的新人,还是工作了一段时间的老人,都会对编写测试用例感到困扰?例如: 固然,编写一份好的测试用例需要:充分的需求分析能力 理论及经验加持,作为测试职场摸爬打滚的老人&…...

【Unity】数据持久化路径Application.persistentDataPath
今天突然想到这个路径Application.persistentDataPath,热更的重要路径,该文件夹可读可写,在移动端唯一一个可读写操作的文件夹。移动端可以将本地的资源(资源MD5值配置表)等一些文件放到StreamingAssets文件夹下&#…...
)
华为OD机试 - 插队(Java JS Python)
题目描述 某银行将客户分为了若干个优先级, 1 级最高, 5 级最低,当你需要在银行办理业务时,优先级高的人随时可以插队到优先级低的人的前面。 现在给出一个人员到来和银行办理业务的时间序列,请你在每次银行办理业务时输出客户的编号。 如果同时有多位优先级相同且最高…...

MongoDB数据库从入门到精通系列之八:调整oplog大小
MongoDB数据库从入门到精通系列之八:调整oplog大小 一、oplog的概念二、oplog大小三、调整oplog大小详细步骤一、oplog的概念 操作日志oplog包含了主节点执行的每一次写操作。oplog是存在于主节点local数据库中的一个固定集合。从节点通过查询此集合以获取需要复制的操作。每个…...

PCL 间接平差法拟合二维直线
目录 一、算法原理二、代码实现三、结果展示四、相关链接一、算法原理 通过传统最小二乘法对点云数据进行二维直线拟合时,可将误差只归因于一个方向上,本文假设误差只存在于 y y y轴方向上,设点云拟合的二维直线方程为: y =...
进程调度的基本过程
这里写目录标题什么是进程进程管理结构体或类的主要属性pid内存指针文件描述符表辅助进程调度的属性并发并行并发什么是进程 进程是操作系统对一个正在运行的程序的一种抽象,也就是说,一个运行起来的程序就是一个进程。 进程又是操作系统进行资源分配的…...

python自动化办公(二)
上接python自动化办公(一) 文章目录文件和目录操作使用shutil库文件查找globfnmatchhashlib文件和目录操作 使用shutil库 shutil库也是Python标准库,它可以处理文件、文件夹、压缩包,能实现文件复制、移动、压缩、解压缩等功能。…...
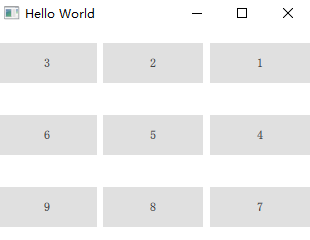
Qt Quick - GridLayout 网格布局
GridLayout 理论总结一、概述二、依赖属性三、例子1. 不含跨行的2. 带跨行列的3. 从右到左一、概述 GridLayout 是最常用的布局器,也叫网格布局器,如果网格布局被调整大小,布局中的所有 Item 将被重新排列。它类似于基于widget的QGridLayout…...
安卓手机也可以使用新必应NewBing
没有魔法安卓手机也可以使用新必应NewBing 目前知道的是安卓手机 安卓手机先安装一个猴狐浏览器 打开手机自带浏览器,搜索关键词:猴狐浏览器,找到官网 也可以直接复制这个网址 狐猴浏览器 lemurbrowser CoolAPK 我的手机是荣耀安卓手机…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
