MongoDB数据库从入门到精通系列之八：调整oplog大小
MongoDB数据库从入门到精通系列之八：调整oplog大小
- 一、oplog的概念
- 二、oplog大小
- 三、调整oplog大小详细步骤
一、oplog的概念
- 操作日志oplog包含了主节点执行的每一次写操作。
- oplog是存在于主节点local数据库中的一个固定集合。
- 从节点通过查询此集合以获取需要复制的操作。
- 每个从节点都维护着自己的oplog，用来记录从主节点复制的每个操作。
- 从节点从同步源中获取操作，将其应用到自己的数据集上，然后再写入oplog中。
二、oplog大小
- 应该将主节点的oplog长度视为维护工作的时间窗口。如果主节点的oplog长度是一小时，那么就只有一小时的时间来修复所有的问题，否则可能会导致从节点落后过多，不得不从头开始重新同步。因此，通常会希望oplog可以保存几天到一周的数据，以便出现问题时给自己一些应对的空间。
- 在oplog被写满之前，没有简单的方法来得出它的长度。WiredTiger存储引擎允许在服务器端运行时在线调整oplog的大小。
- 应该首先在每个从节点成员上执行这些步骤。只有完成了从节点上的变更后，才可以对主节点进行更改。
- 每个可能成为主节点的服务器都应该拥有足够大的oplog，以便提供足够的时间窗口进行维护。
三、调整oplog大小详细步骤
要增加oplog的大小，
相关文章：
MongoDB数据库从入门到精通系列之八：调整oplog大小
MongoDB数据库从入门到精通系列之八：调整oplog大小 一、oplog的概念二、oplog大小三、调整oplog大小详细步骤一、oplog的概念 操作日志oplog包含了主节点执行的每一次写操作。oplog是存在于主节点local数据库中的一个固定集合。从节点通过查询此集合以获取需要复制的操作。每个…...
PCL 间接平差法拟合二维直线
目录 一、算法原理二、代码实现三、结果展示四、相关链接一、算法原理 通过传统最小二乘法对点云数据进行二维直线拟合时，可将误差只归因于一个方向上，本文假设误差只存在于 y y y轴方向上，设点云拟合的二维直线方程为： y =...
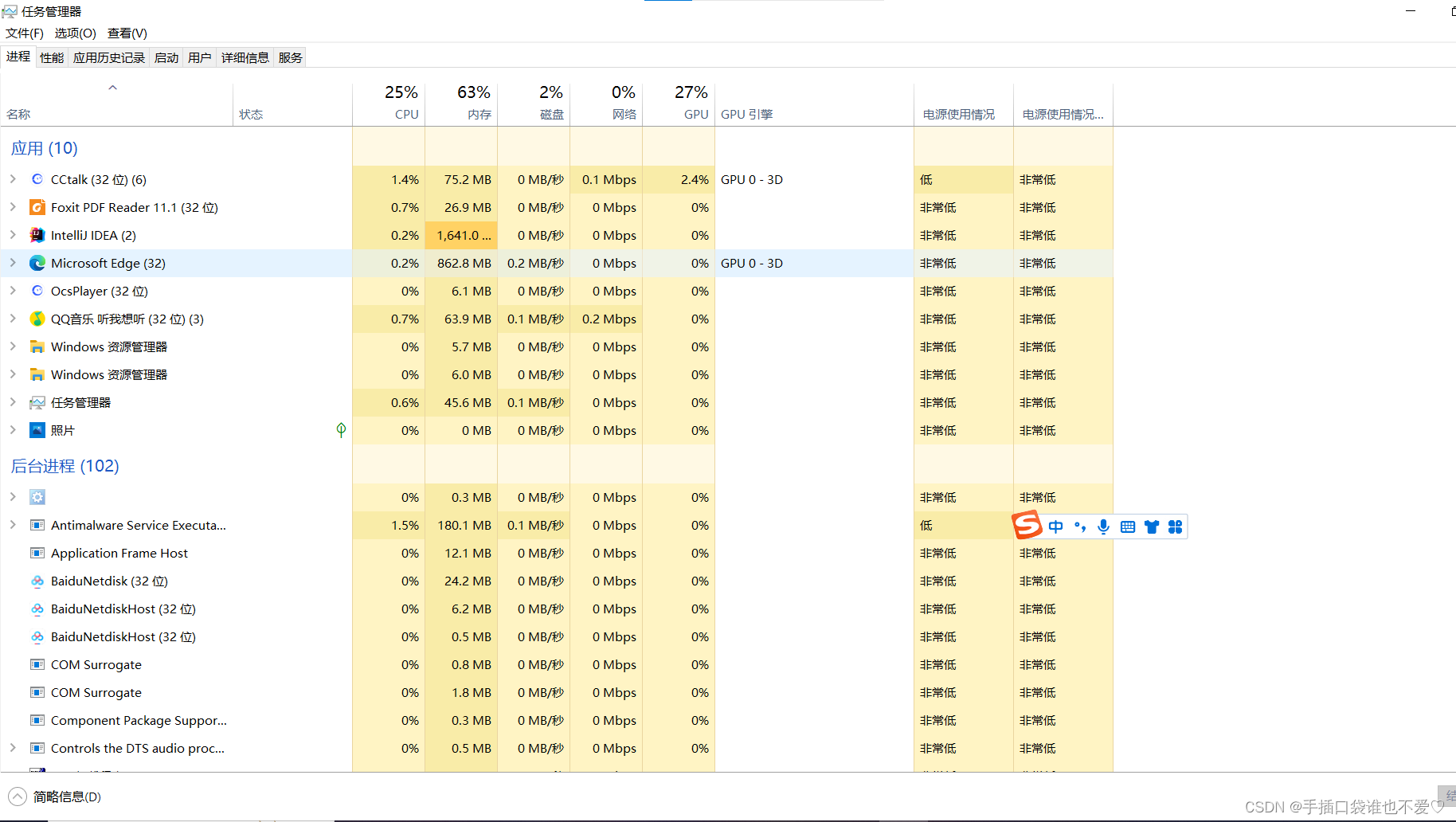
进程调度的基本过程
这里写目录标题什么是进程进程管理结构体或类的主要属性pid内存指针文件描述符表辅助进程调度的属性并发并行并发什么是进程 进程是操作系统对一个正在运行的程序的一种抽象，也就是说，一个运行起来的程序就是一个进程。 进程又是操作系统进行资源分配的…...
python自动化办公（二）
上接python自动化办公（一） 文章目录文件和目录操作使用shutil库文件查找globfnmatchhashlib文件和目录操作 使用shutil库 shutil库也是Python标准库，它可以处理文件、文件夹、压缩包，能实现文件复制、移动、压缩、解压缩等功能。…...
Qt Quick - GridLayout 网格布局
GridLayout 理论总结一、概述二、依赖属性三、例子1. 不含跨行的2. 带跨行列的3. 从右到左一、概述 GridLayout 是最常用的布局器，也叫网格布局器，如果网格布局被调整大小，布局中的所有 Item 将被重新排列。它类似于基于widget的QGridLayout…...
安卓手机也可以使用新必应NewBing
没有魔法安卓手机也可以使用新必应NewBing 目前知道的是安卓手机 安卓手机先安装一个猴狐浏览器 打开手机自带浏览器，搜索关键词：猴狐浏览器，找到官网 也可以直接复制这个网址 狐猴浏览器 lemurbrowser CoolAPK 我的手机是荣耀安卓手机…...
支付系统设计：消息重试组件封装
文章目录前言一、重试场景分析一、如何实现重试1. 扫表2. 基于中间件自身特性3. 基于框架4. 根据公司业务特性自己实现的重试二、重试组件封装1. 需求分析2. 模块设计2.1 持久化模块1. 表定义2. 持久化接口定义3. 持久化配置类2.2 重试模块1.启动2.重试3. 业务端使用1. 引入依赖…...
Visual Studio 2022 c#中很实用的VS默认快捷键和原生功能
常常使用VS感觉还是有必要掌握其默认的快捷键，我这个人比较懒，不喜欢动不动就去设置快捷键，系统有就用，记住了就可以到处用，问题是像我们这种有很多个工作场所的人不可能每台电脑都去配置一下快键键。实际上我使用3dma…...
Python的30个编程技巧
1. 原地交换两个数字 Python 提供了一个直观的在一行代码中赋值与交换（变量值）的方法，请参见下面的示例： x,y 10,20 print(x,y) x,y y,x print(x,y) #1 (10, 20) #2 (20, 10) 赋值的右侧形成了一个新的元组，左侧立即解…...
MySQL：JDBC
什么是JDBC？ JDBC( Java DataBase Connectivity ) 称为 Java数据库连接 ，它是一种用于数据库访问的应用程序 API ，由一组用Java语言编写的类和接口组成，有了JDBC就可以 用统一的语法对多种关系数据库进行访问，而不用担…...
C++【list容器模拟实现函数解析】
list容器&&模拟实现函数解析 文章目录list容器&&模拟实现函数解析一、list容器使用介绍二、list容器模拟实现及函数解析2.1 list结构体创建2.2 迭代器封装2.21 构造函数：2.22 前置和后置及- -2.23 解引用2.24 判断相等2.25 箭头重载2.26 第二个和第…...
（Java）试题 算法提高 约数个数
一、题目 （1）资源限制 内存限制：512.0MB C/C时间限制：1.0s Java时间限制：3.0s Python时间限制：5.0s （2）输入 输入一个正整数N （3）输出 N有几个约数 &a…...
魔法反射--java反射初入门(基础篇)
👳我亲爱的各位大佬们好😘😘😘 ♨️本篇文章记录的为 java反射初入门 相关内容，适合在学Java的小白,帮助新手快速上手,也适合复习中，面试中的大佬🙉🙉🙉。 ♨️如果文章有…...
概率统计_协方差的传播 Covariance Propagation
1. 方差的传播 误差的传播是指分析在形如的关系中，参量误差(x)对变量误差(y)的影响有多大。误差的传播与函数的微分紧密相关，本质是在利用当Δ x 不大时，。 方差计算公式： X为变量，为总体均值，N为总体例数。求变量X与均值的差的平方再求平均值，即得到方差。方差…...
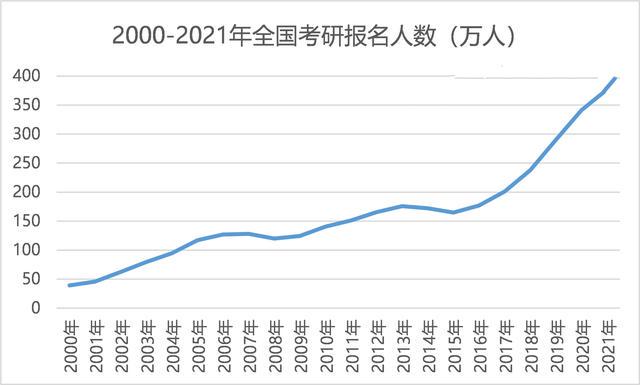
大学生考研的意义？
当我拿起笔头，准备写这个话题时，心里是非常难受的，因为看到太多的学生在最好的年华，在自由的大学本应该开拓知识，提升认知，动手实践，不断尝试和试错，不断历练自己跳出学生思维圈&…...
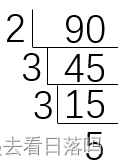
【C++笔试强训】第三十一天
🎇C笔试强训 博客主页：一起去看日落吗分享博主的C刷题日常，大家一起学习博主的能力有限，出现错误希望大家不吝赐教分享给大家一句我很喜欢的话：夜色难免微凉，前方必有曙光 🌞。 选择题 &#x…...
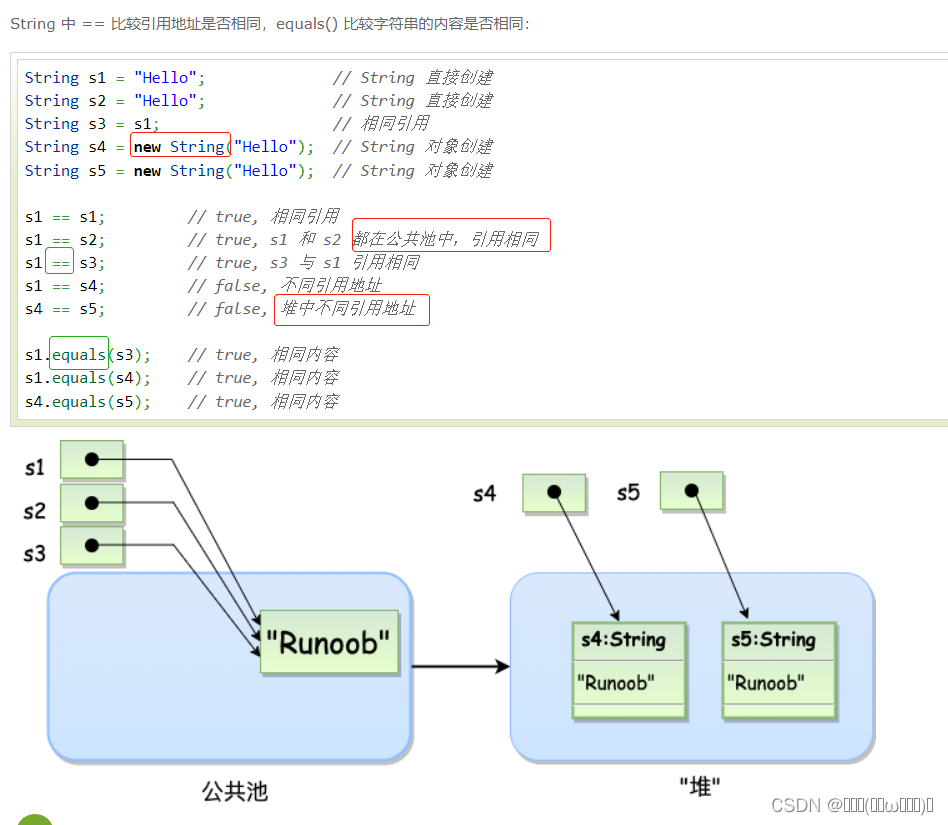
toString()、equals()是什么，为啥需要重写，多种方法来重写
https://m.runoob.com/java/java-object-class.html toString() 1.为什么会有toString 子类继承父类就可以使用父类所有非私有的属性的方法。 在Java中所有类都直接或者间接继承Object类，可以说只要是Object类里面定义的非私有的属性和方法，任何类都可…...
家装材料清单中会有哪些装饰材料？
在家居装修中，业主可以根据装修公司出具的材料清单去一一采购，这样不至于有遗漏，就算采用全包的方式，通过材料清单也可以大致了解当时房子装修所用的材料，补充自己的装修知识。下面跟随小编一起了解下房子装修材料中所…...
【C++初阶】6. CC++内存管理
1. C/C内存分布 我们先来看下面的一段代码和相关问题 int globalVar 1; static int staticGlobalVar 1; void Test() {static int staticVar 1;int localVar 1;int num1[10] { 1, 2, 3, 4 };char char2[] "abcd";const char* pChar3 "abcd";int* …...
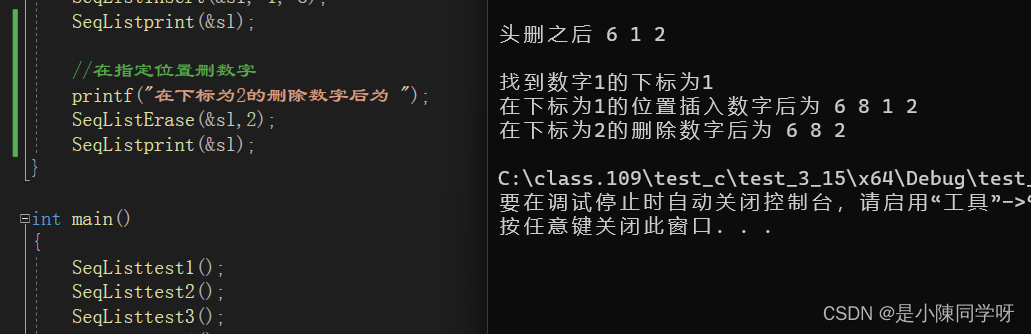
【数据结构】万字超详解顺序表（比细狗还细）
我这个人走得很慢，但是我从不后退。 ——亚伯拉罕林肯 目录 一.什么是线性表？ 二.什么是顺序表？ 三.接口函数的实现 1.创建工程 2.构造顺序表 3.初始化顺序表 3.初始化顺序表 4.顺序表的尾插 5.顺序…...
什么是库存周转？如何用进销存系统提高库存周转率？
你可能听说过这样一句话： “利润不是赚出来的，是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业，很多企业看着销售不错，账上却没钱、利润也不见了，一翻库存才发现： 一堆卖不动的旧货…...
（转）什么是DockerCompose?它有什么作用？
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用，而无需手动一个个创建和运行容器。 Compose文件是一个文本文件，通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...
均衡后的SNRSINR
本文主要摘自参考文献中的前两篇，相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程，其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线， n r n_r nr 根接收天线的 MIMO 系…...
AI，如何重构理解、匹配与决策？
AI 时代，我们如何理解消费？ 作者｜王彬 封面｜Unplash 人们通过信息理解世界。 曾几何时，PC 与移动互联网重塑了人们的购物路径：信息变得唾手可得，商品决策变得高度依赖内容。 但 AI 时代的来…...
短视频矩阵系统文案创作功能开发实践，定制化开发
在短视频行业迅猛发展的当下，企业和个人创作者为了扩大影响力、提升传播效果，纷纷采用短视频矩阵运营策略，同时管理多个平台、多个账号的内容发布。然而，频繁的文案创作需求让运营者疲于应对，如何高效产出高质量文案成…...
PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题， 因为搜索范围是有界的，上界最大木板长度补充的全部木料长度，下界最小木板长度； 即left0,right10^6; 我们可以设置一个候选值x(mid)，将木板的长度全部都补充到x，如果成功…...
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别（二）
在上一篇文章中，我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调，以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后，如何调用这个模型进行人脸情感识别的具体代码实现，包括详细的步骤和注释。 模型调用步骤 环境准备：确保安装了必要的Python库。…...