Linux C++ 053-设计模式之模板方法模式
Linux C++ 053-设计模式之模板方法模式
本节关键字:Linux、C++、设计模式、模板方法模式
相关库函数:
概念
模板方法模式定义了一个算法的步骤,并允许子类别为一个或多个步骤提供其实践方式。让子类别在不改变算法架构的情况下,重新定义算法中的某些步骤。在软件工程中,它是一种软件设计模式,和C++模板没有关连。
使用场景
模板方法模式多用在:
1、某些类别的算法中,实做了相同的方法,造成程式码的重复。
2、控制子类别必须遵守的一些事项。
代码示例
// 将不变的代码都移到父类中,将可变的方法用virture留到子类中重写
// 需要重写的方法都放在了protected关键字下
// 父类中无需重写的方法来调用需要重写的方法
// 客户端只需访问类中无需重写的方法class Computer
{
public:void product() {installCPU();installRAM();installGraphicsCard();}
private:virtual void installCPU() = 0;virtual void installRAM() = 0;virtual void installGraphicsCard() = 0;
};
class ComputerA : public Computer
{
protected:void installCPU() override {cout << "ComputerA install Inter Core i5" << endl;}void installRAM() override {cout << "ComputerA install 2G Ram" << endl;}void installGraphicsCard() override {cout << "ComputerA install Gtx940 GraohicsCard" << endl;}
};
class ComputerB : public Computer
{
protected:void installCPU() override {cout << "ComputerB install Inter Core i7" << endl;}void installRAM() override {cout << "ComputerB install 4G Ram" << endl;}void installGraphicsCard() override {cout << "ComputerB install Gtx960 GraohicsCard" << endl;}
};
int main_Model()
{ComputerB* c1 = new ComputerB();c1->product();c1 = NULL;return 0;
}
/* 运行结果:
ComputerB install Inter Core i7
ComputerB install 4G Ram
ComputerB install Gtx960 GraphicsCard
*/
相关文章:

Linux C++ 053-设计模式之模板方法模式
Linux C 053-设计模式之模板方法模式 本节关键字:Linux、C、设计模式、模板方法模式 相关库函数: 概念 模板方法模式定义了一个算法的步骤,并允许子类别为一个或多个步骤提供其实践方式。让子类别在不改变算法架构的情况下,重新…...
【Python 项目】类鸟群:仿真鸟群
类鸟群:仿真鸟群 仔细观察一群鸟或一群鱼,你会发现,虽然群体由个体生物组成,但该群体作为一个整体似乎有它自己的生命。鸟群中的鸟在移动、飞越和绕过障碍物时,彼此之间相互定位。受到打扰或惊吓时会破坏编队…...

基于信号处理的PPG信号滤波降噪方法(MATLAB)
光电容积脉搏波PPG信号结合相关算法可以用于人体生理参数检测,如血压、血氧饱和度等,但采集过程中极易受到噪声干扰,对于血压、血氧饱和度测量的准确性造成影响。随着当今社会医疗保健技术的发展,可穿戴监测设备对于PPG信号的质量…...

新一代信息技术及应用
关于云计算的描述不正确的是( )。 A 云计算可以通过网络连接,用户通过网络接入“云”中并获得有关的服务,“云”内节点之间也通过内部的网络相连 B 云计算可以快速、按需、弹性服务,用户可以按照实际需求迅速获取或释放…...

SVN 解决冲突
SVN 解决冲突 1. 引言 在软件开发过程中,版本控制是一个至关重要的环节。SVN(Subversion)作为一个流行的版本控制系统,被广泛应用于团队协作中。然而,当多个开发者同时对同一部分代码进行修改时,冲突是不可避免的。本文将详细介绍如何在SVN中解决这些冲突,以便团队成员…...

机器人前沿--PalmE:An Embodied Multimodal Language Model 具身多模态大(语言)模型
首先解释这篇工作名称Palm-E,发表时间为2023.03,其中的Palm是谷歌内部在2022.04开发的大语言模型,功能类似ChatGPT,只是由于各种原因没有那样火起来,E是Embodied的首字母,翻译过来就是具身多模态大语言模型…...

编程语言都是哪些人开发出来的?为什么都是国外较小国家的人
编程语言都是哪些人开发出来的? 编程语言的开发者通常是来自计算机科学、软件工程、数学、物理学等领域的专家、学者和工程师。这些开发者具备深厚的编程技能、算法知识、系统设计能力以及创新思维,他们致力于创造出能够解决特定问题或满足特定需求的编…...
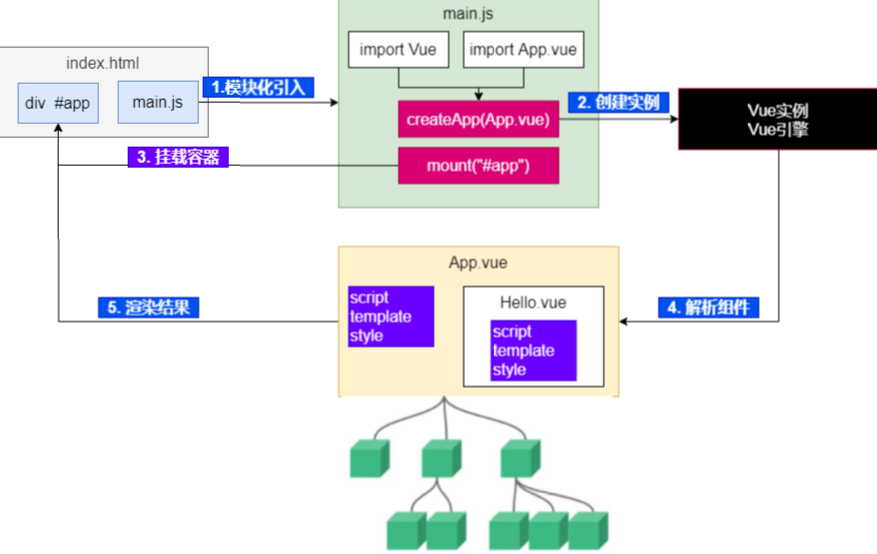
【前端速通系列|第二篇】Vue3前置知识
文章目录 1.前言2.包管理工具npm2.1下载node.js2.2配置 npm 镜像源2.3 npm 常用命令 3.Vite构建工具4.Vue3组件化5.Vue3运行原理 1.前言 本系列文章旨在帮助大家快速上手前端开发。 2.包管理工具npm npm 是 node.js中进行 包管理 的工具. 类似于Java中的Maven。 2.1下载nod…...
)
ES6 Module 的语法(十二)
ES6(ECMAScript 2015)引入了模块(Modules)的概念,使得JavaScript代码可以更容易地组织和复用。 1. export 关键字 命名导出 (Named Exports) 你可以使用 export 关键字导出多个变量、函数或类。 // module.js export…...

Redis 主从复制,哨兵与集群
目录 一.redis主从复制 1.redis 主从复制架构 2.主从复制特点 3.主从复制的基本原理 4.命令行配置 5.实现主从复制 6.删除主从复制 7.主从复制故障恢复 8.主从复制完整过程 9.主从同步优化配置 二.哨兵模式(Sentinel) 1.主要组件和概念 2.哨…...

CV05_深度学习模块之间的缝合教学(1)
1.1 在哪里缝 测试文件?() 训练文件?() 模型文件?(√) 1.2 骨干网络与模块缝合 以Vision Transformer为例,模型文件里有很多类,我们只在最后…...

【密码学】公钥密码的基本概念
在先前我写的密码学体制文章中谈到,现代密码学分为两大体制,介绍了一些有关对称密码体制诸如流密码和分组密码的内容。本文的主要内容则切换到公钥密码体制(又称非对称密码体制),简述了公钥密码体制的基本思想和应用方…...

【前端项目笔记】10 项目优化上线
项目优化上线 目标:优化Vue项目部署Vue项目(上线提供使用) 项目优化 项目优化策略: 生成打包报告:根据生成的报告发现问题并解决第三方库启用CDN:提高首屏页面的加载效率Element-UI组件按需加载路由懒加…...

Qt基础控件总结—多页面切换(QStackWidget类、QTabBar类和QTabWidget类)
QStackedWidget 类 QStackedWidget 类是在 QStackedLayout 之上构造的一个便利的部件,其使用方法与步骤和 QStackedLayout 是一样的。QStackedWidget 类的成员函数与 QStackedLayout 类也基本上是一致的,使用该类就和使用 QStackedLayout 一样。 使用该类可以参考QStackedL…...

团队融合与业务突破
结束了在上海久事集团下属公司的《团队融合与业务突破》课程,不仅探讨了团队领导力的关键技巧,更重要的是,我们从业务协同的视角,在跨团队中如何达成了共识,结合系统思考的相关内容,让大家看到跨部门冲突的…...

mybatilsplaus 常用注解
官网地址 baomidou注解配置...

vue引入sm-crypto通过sm4对文件进行加解密,用户输入密码
对文件加密并保存: import { sm4 } from sm-cryptofetch("你的文件地址") .then(response > response.blob()) .then(byteStream > {const reader2 new FileReader();reader2.onload function(event) {const arrayBuffer event.target.result;l…...

vue3实现无缝滚动列表(大屏数据轮播场景)
实现思路 vue3目前可以通过第三方组件来实现这个需求。 下面介绍一下这个第三方滚动组件--vue3-scroll-seamless vue3-scroll-seamless 是一个用于 Vue 3 的插件,用于实现无缝滚动的组件。它可以让内容在水平或垂直方向上无缝滚动,适用于展示轮播图、新…...

element ui ts table重置排序
#日常# 今天带的实习生,在遇到开发过程中,遇到了element ui table 每次查询的时候都需要重置排序方式,而且多个排序是由前端排序。 <el-table :data"tableData" ref"restTable"> </<el-table> <script…...

python热门面试题三
面试题1:Python中的列表推导式是什么?请给出一个例子。 回答: 列表推导式(List Comprehension)是Python中一种非常强大且简洁的构建列表的工具。它允许你通过一个表达式来创建一个新的列表,这个表达式定义…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...
