ArkTS学习笔记_封装复用之@Styles装饰器
ArkTS学习笔记_封装复用之@Styles装饰器
- 背景:
在开发中,如果每个组件的样式都需要单独设置,就会出现大量代码在进行重复样式设置,虽然可以复制粘贴,但为了代码简洁性和后续方便维护,给出的思路是:提炼和封装相同的样式成方法,方便复用调用,装饰器@Style孕育而生。 - 作用:
@Styles装饰器可以将多条样式设置,提炼成一个方法,直接在组件使用的位置调用即可复用。通过@Styles装饰器可以快速定义并复用自定义样式。用于快速定义并复用自定义样式。
一、@Styles装饰器使用说明
- 当前@Styles仅支持通用属性和通用事件。
- @Styles方法不支持参数,反例如下。
// 反例: @Styles不支持参数
@Styles function globalFancy (value: number) {.width(value)
}
- @Styles可以定义在组件内或全局。
在全局定义时需在方法名前面添加function关键字,组件内定义时则不需要添加function关键字。
// 全局,前面添加function关键字
@Styles function functionName() { ... }// 在组件内
@Component
struct FancyUse {// 组件内部,不需要添加function关键字 @Styles fancy() {.height(100)}}
- 定义在组件内的@Styles可以通过this访问组件的常量和状态变量,并可以在@Styles里通过事件来改变状态变量的值。
@Component
struct FancyUse {@State heightValue: number = 100@Styles fancy() {.height(this.heightValue) // 可是使用this指向组件本身,调用组件的状态 .backgroundColor(Color.Yellow).onClick(() => {this.heightValue = 200 // 可是使用this指向组件本身,给组件的状态赋值 })}
}
- 组件内@Styles的优先级高于全局@Styles。框架优先找当前组件内的@Styles,如果找不到,则会全局查找。
二、以下示例中演示了组件内@Styles和全局@Styles的用法
// 定义在全局的@Styles封装的样式
@Styles function globalFancy () {.width(150).height(100).backgroundColor(Color.Pink)
}@Entry
@Component
struct FancyUse {@State heightValue: number = 100// 定义在组件内的@Styles封装的样式@Styles fancy() {.width(200).height(this.heightValue).backgroundColor(Color.Yellow).onClick(() => {this.heightValue = 200})}build() {Column({ space: 10 }) {Text('FancyA').globalFancy() // 和方法一样,调用使用全局的@Styles封装的样式.fontSize(30)Text('FancyB').fancy() // 和方法一样,使用组件内的@Styles封装的样式.fontSize(30)}}
}
相关文章:

ArkTS学习笔记_封装复用之@Styles装饰器
ArkTS学习笔记_封装复用之Styles装饰器 背景: 在开发中,如果每个组件的样式都需要单独设置,就会出现大量代码在进行重复样式设置,虽然可以复制粘贴,但为了代码简洁性和后续方便维护,给出的思路是ÿ…...

根据vue学习react
react的函数式组件与vue2是很像的 一、基础类似点 1、组件下拥有一个根节点,vue2是template,react是幽灵标签<> 2、vue2是{{}}以及v-model,react的绑定是{} 3、vue2编译html是v-html,react是{},并且react的jsx中…...
Hi3861 OpenHarmony嵌入式应用入门--HTTPD
httpd 是 Apache HTTP Server 的守护进程名称,Apache HTTP Server 是一种广泛使用的开源网页服务器软件。 本项目是从LwIP中抽取的HTTP服务器代码; Hi3861 SDK中已经包含了一份预编译的lwip,但没有开启HTTP服务器功能(静态库无法…...
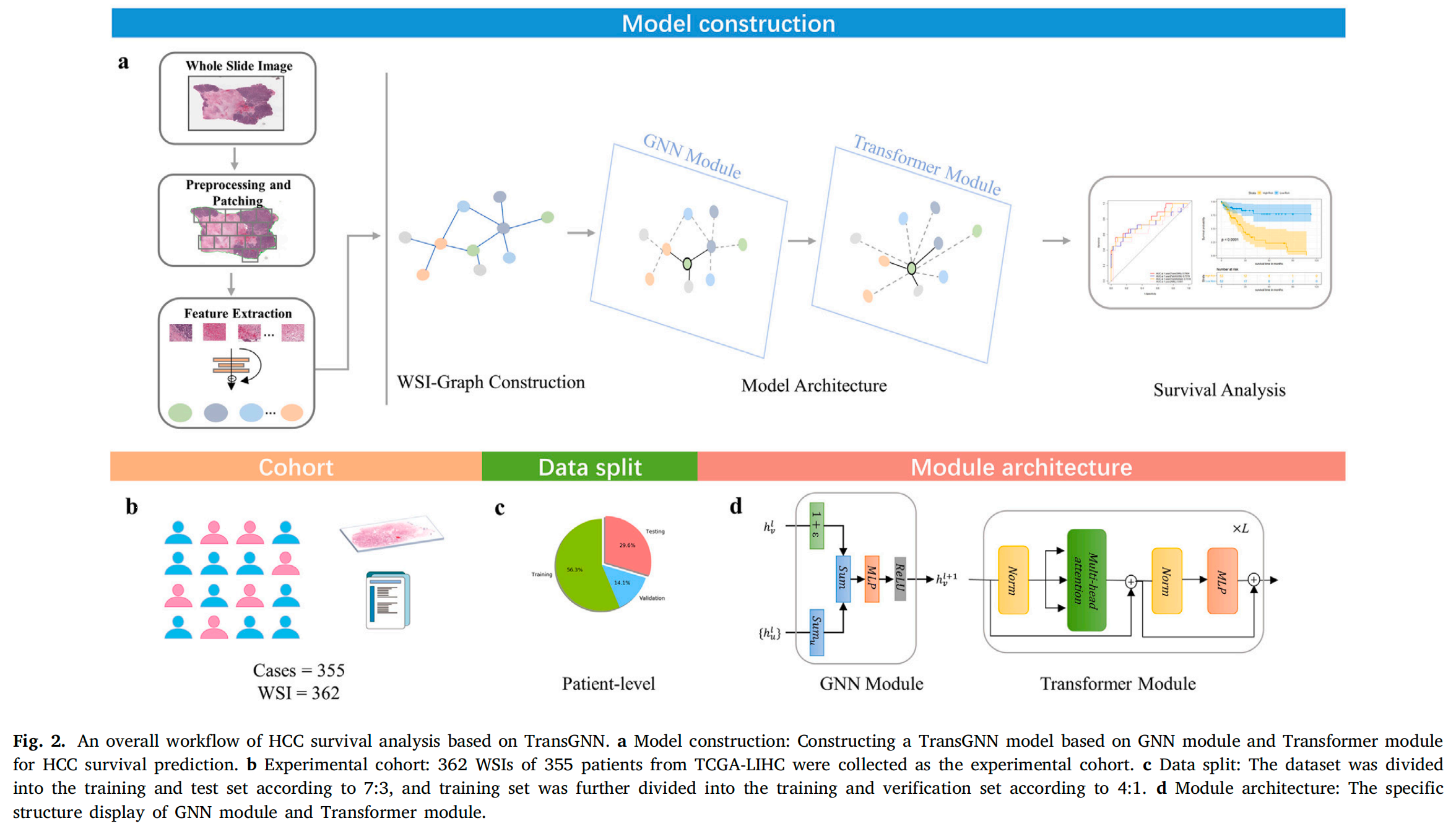
MICS2024|少样本学习、多模态技术以及大语言模型在医学图像处理领域的研究进展|24-07-14
小罗碎碎念 本期推文主题 今天的会议很多主题都集中在大模型、多模态这两个方面,很明显,这两个方向都是目前的研究热点。 所以,我这一期推文会先简单的分析一下秦文健(中科院)和史淼晶(同济大学)…...
ConfigMap-secrets-静态pod
一.ConfigMap 1.概述 ConfigMap资源,简称CM资源,它生成的键值对数据,存储在ETCD数据库中 应用场景:主要是对应用程序的配置 pod通过env变量引入ConfigMap,或者通过数据卷挂载volume的方式引入ConfigMap资源 官方解释…...

SQL Error: 1406, SQLState: 22001
SQL错误代码1406和SQLState 22001通常表示“列数据过长”错误。这意味着尝试插入或更新列中的值,但该值的长度超过了该列允许的最大长度。 解决此问题的几个步骤: 检查列长度: 确定引起错误的列。检查数据库架构中该列允许的最大长度。 验证…...
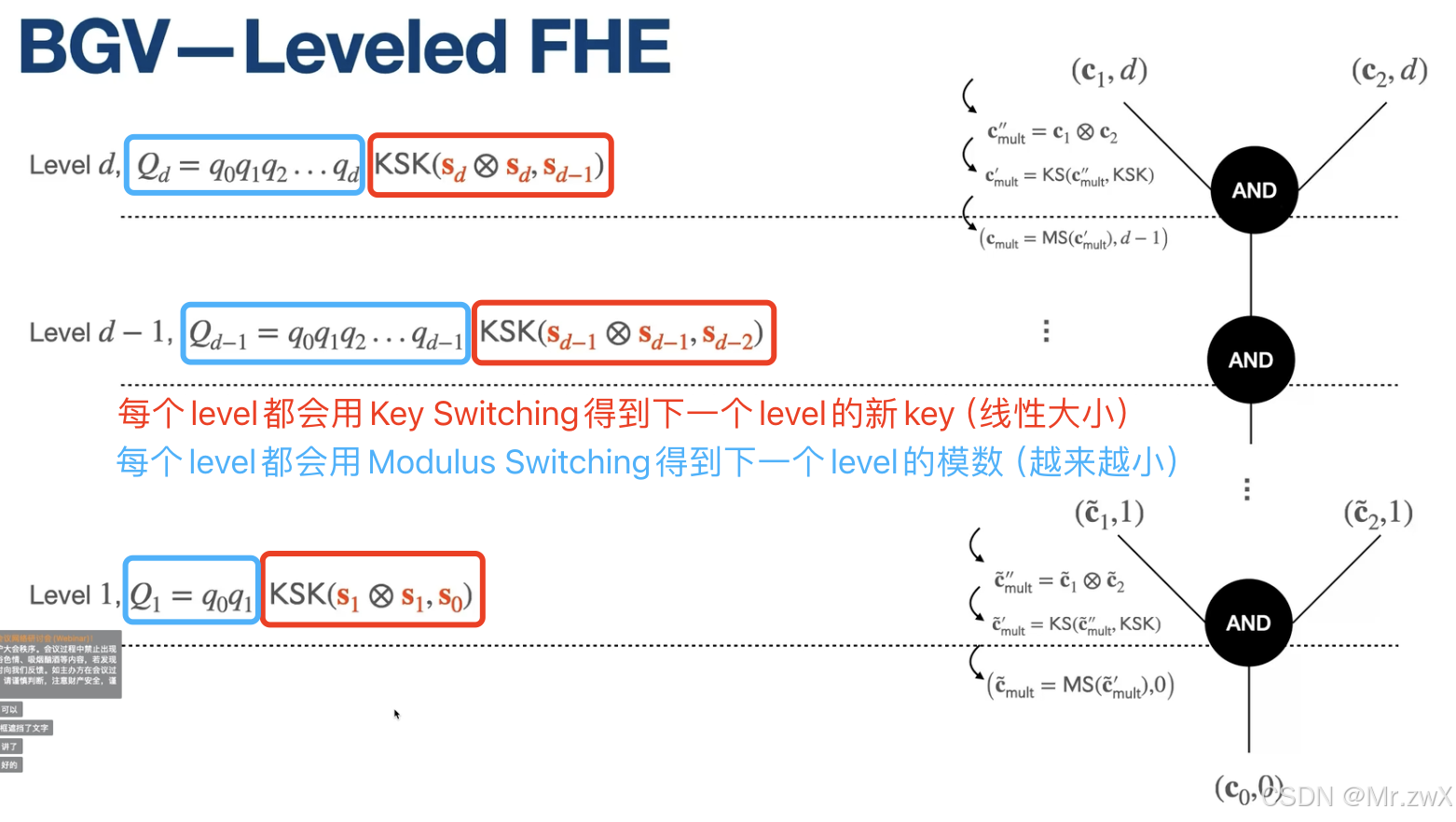
【密码学基础】基于LWE(Learning with Errors)的全同态加密方案
学习资源: 全同态加密I:理论与基础(上海交通大学 郁昱老师) 全同态加密II:全同态加密的理论与构造(Xiang Xie老师) 现在第二代(如BGV和BFV)和第三代全同态加密方案都是基…...
Linux - 基础开发工具(yum、vim、gcc、g++、make/Makefile、git)
目录 Linux软件包管理器 - yum Linux下安装软件的方式 认识yum 查找软件包 安装软件 如何实现本地机器和云服务器之间的文件互传 卸载软件 Linux编辑器 - vim vim的基本概念 vim下各模式的切换 vim命令模式各命令汇总 vim底行模式各命令汇总 vim的简单配置 Linux编译器 - gc…...

网络安全法律框架更新:最新合规要求与企业应对策略
网络安全法律框架的最新更新 近期,中国的网络安全法律框架经历了重要的更新。2022年,《网络安全法》迎来了首次修改,这一修订主要是为了与《数据安全法》和《个人信息保护法》等新实施的法律进行衔接协调,完善法律责任制度&#x…...

数仓工具—Hive语法之正则表达式函数
正则表达式函数 之前我们介绍过like rlike regexp 这些关键字,都是和匹配有关的,今天我们介绍一下hive 的REGEXP_REPLACE 和REGEXP_EXTRACT 函数,背景是使用Hive正则表达式函数提取数字 在我的其他文章中,我们已经看到了如何使用Hive正则表达式从字符串中提取日期值。正则…...

WKCTF 2024 easy_heap
很经典的house of orange unsortedbin attack FSOP 变量覆盖 不能 free,那首先想到就是 house of orange泄露Libc基址,然后unsortedbin attack。 但是只能show(8),就不能用largebin的套路来泄露堆地址了,那怎么办呢? …...

SQL 多变关联使用子查询去重
不去重状态 select a.*,b.recon_amt from free_settlement_first aleft join free_settlement_second b on a.settlement_first_id b.settlement_first_id 有2条数据出现了重复 使用子查询去重 select a.*,b.recon_amt from free_settlement_first aleft join free_settlem…...
)
php表单提交并自动发送邮件给某个邮箱(示例源码下载)
只需要将以下代码内容进行复制即可用到自己的程序/API接口中: <?php if(!empty($_POST[is_post]) && $_POST[is_post]1){$url "https://www.aoksend.com/index/api/send_email";$name $_POST[name];$email $_POST[email];$subject $_POS…...

论文翻译:Large Language Models for Education: A Survey
目录 大型语言模型在教育领域的应用:一项综述摘要1 引言2. 教育中的LLM特征2.1. LLMs的特征2.2 教育的特征2.2.1 教育发展过程 低进入门槛。2.2.2. 对教师的影响2.2.3 教育挑战 2.3 LLMEdu的特征2.3.1 "LLMs 教育"的具体体现2.3.2 "LLMs 教育"…...

7.13实训日志
上午 学习网络安全的过程中,我们深入了解了网络的不同层面和技术,从表层网络到深网再到暗网,以及涉及的产业分类和技术工具。这些知识不仅帮助我们理解网络的复杂性,还揭示了如何应对和防范各种网络威胁。 首先,我们…...

【力扣】每日一题—第70题,爬楼梯
题目: 假设你正在爬楼梯。需要n阶你才能到达楼顶。 每次你可以爬1或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 思路: 我开始是写了一个函数计算爬一层和爬二层的个数,之后排列求和,但是超范围了,…...

Docker修改国内镜像源
如果docker已将安装好 参考:https://github.com/cmliu/CF-Workers-docker.io sudo mkdir -p /etc/dockercd /etc/dockersudo vim daemon.json #输入以下内容 { "registry-mirrors": ["https://docker.fxxk.dedyn.io"] } #重启docker服务 su…...

安防监控视频平台LntonCVS视频融合共享平台智慧消防实现远程集中视频监控方案
近年来,电力系统内变电站着火事件频发,这对消防安全管理提出了严峻挑战。我国消防安全基础设施不完善、管理机制不健全、应急处置能力不足及公众消防安全意识淡薄等问题,严重制约了消防安全的提升。因此,加强变电站的消防安全管理…...

【大模型LLM面试合集】大语言模型架构_layer_normalization
2.layer_normalization 1.Normalization 1.1 Batch Norm 为什么要进行BN呢? 在深度神经网络训练的过程中,通常以输入网络的每一个mini-batch进行训练,这样每个batch具有不同的分布,使模型训练起来特别困难。Internal Covariat…...

OpenGL笔记八之EBO和EBO绘制流程
OpenGL笔记八之EBO和EBO绘制流程 —— 2024-07-07 晚上 bilibili赵新政老师的教程看后笔记 code review! 文章目录 OpenGL笔记八之EBO和EBO绘制流程1.EBO2.glDrawElements:如果使用了ebo,最后一个参数可以写03.glDrawElements:如果使用了e…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...
