当前位置： 首页 > news >正文

如何将VirtualBox虚拟机转换到VMware中

news 2026/2/8 18:40:45

转换前的准备
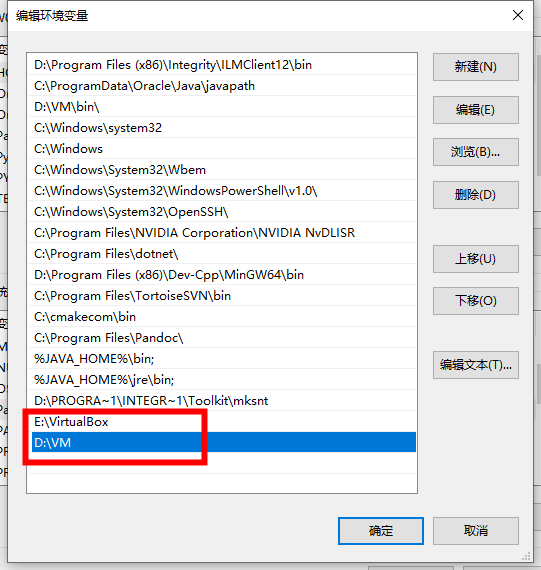
首先需要你找到你的virtualbox以及VM安装到哪个文件夹里了，需要将这两个文件夹添加进环境变量Path中。

如果你记不清了，可以用everything全局搜索一下“VBoxManage.exe’以及“vmware-vdiskmanager.exe”，看一眼这个程序放到哪个目录下了，哪个就是安装目录。然后复制这个路径，添加到path中。
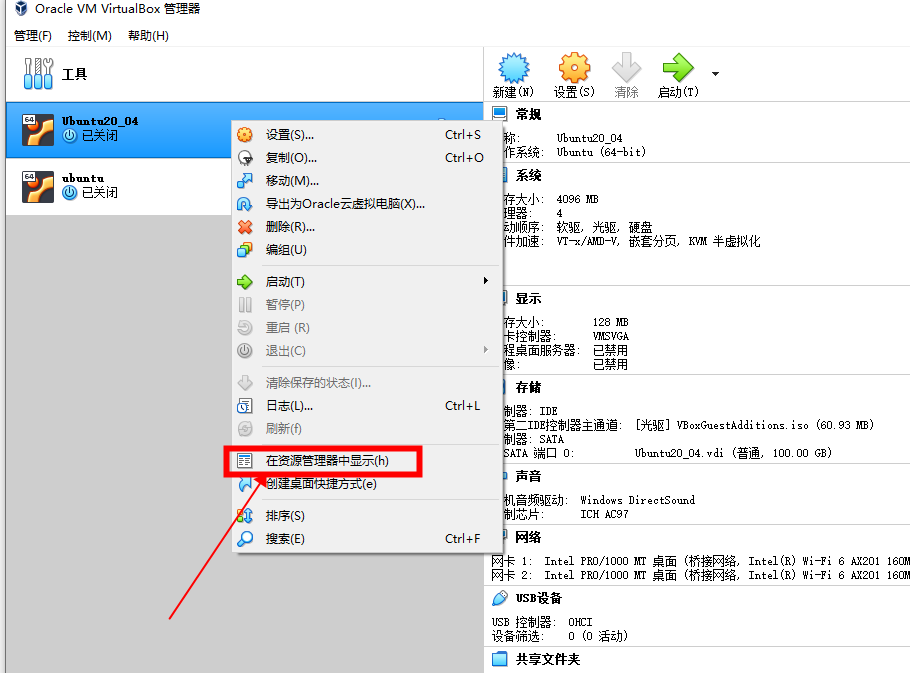
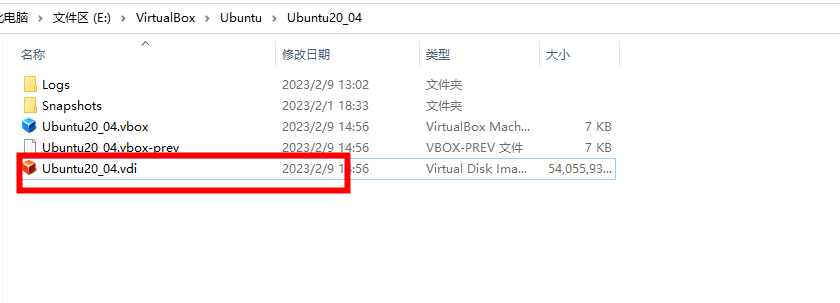
在这里插入图片描述

一、进入资源目录
在这里插入图片描述
在这里插入图片描述
记住这个文件的路径以及名称
二、第一次转换
打开cmd
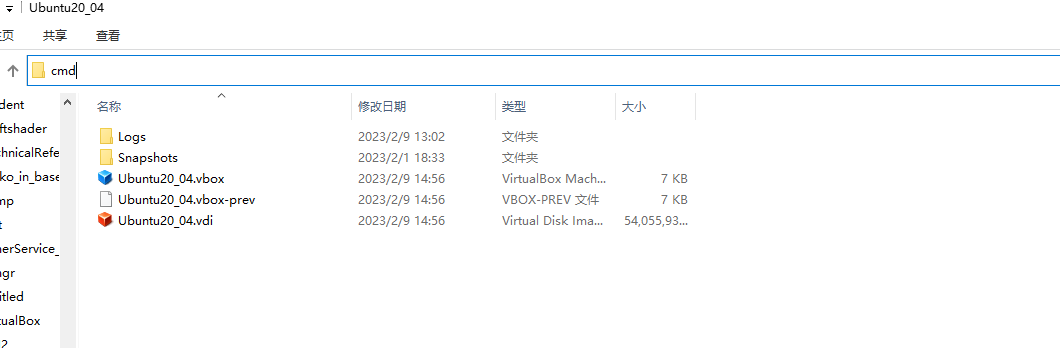
在这里插入图片描述
键入转换命令
(不用加引号，此处引号是为了方便观看)

VBoxManage.exe clonehd “vdi文件(要包括其所在位置)” “vmdk文件(输入你想要存储的vmdk位置以及名字)” --format VMDK

注：这两个文件记得要带上后缀
例如：

VBoxManage.exe clonehd    E:\VirtualBox\Ubuntu\Ubuntu20_04\Ubuntu20_04.vdi   D:\Ubuntu\Ubuntu20_04.vmdk  --format VMDK

注意：你的转换后的文件需要放在一个磁盘空间足够大的盘中。否则的话会转换失败。
在这里插入图片描述
之后得到vmdk文件：
在这里插入图片描述
但此时的vmdk用vm打开还并不能用，还需要用vm的一项功能再转换一次。
三、第二次转换
转换命令：
vmware-vdiskmanager.exe -r “刚才生成的vmdk文件” -t 0 “.com.vmdk文件”
我的指令如下：

vmware-vdiskmanager.exe  -r  "D:\Ubuntu\Ubuntu20_04.vmdk"  -t  0  "D:\Ubuntu\Ubuntu20_04.vmdk.com.vmdk"

在这里插入图片描述
在这里插入图片描述
四、导入虚拟机
该文件就可以用于vm虚拟机了，接下来打开VMware，文件>>新建虚拟机
在这里插入图片描述
之后按你所需要的设定虚拟机配置：
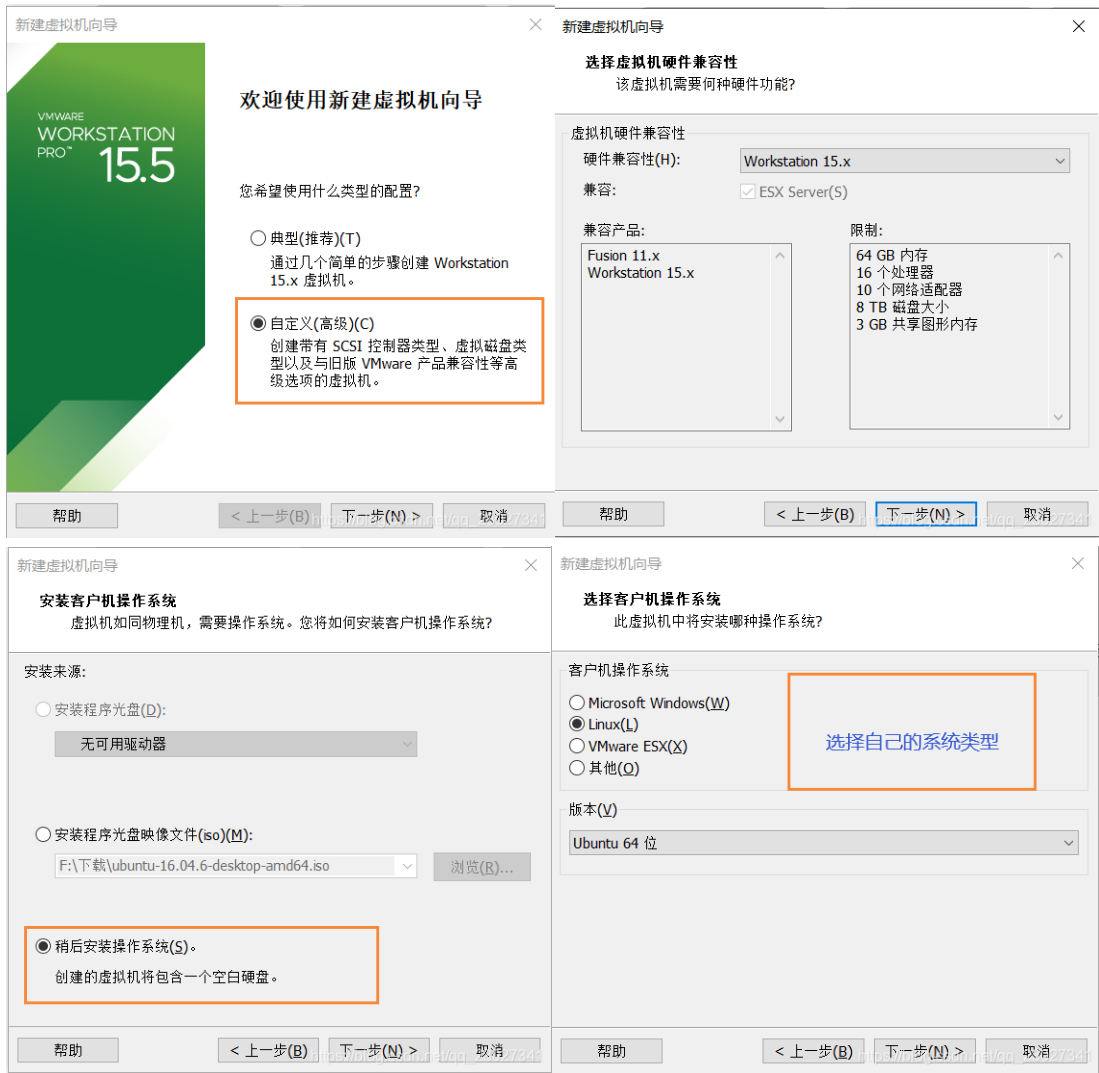
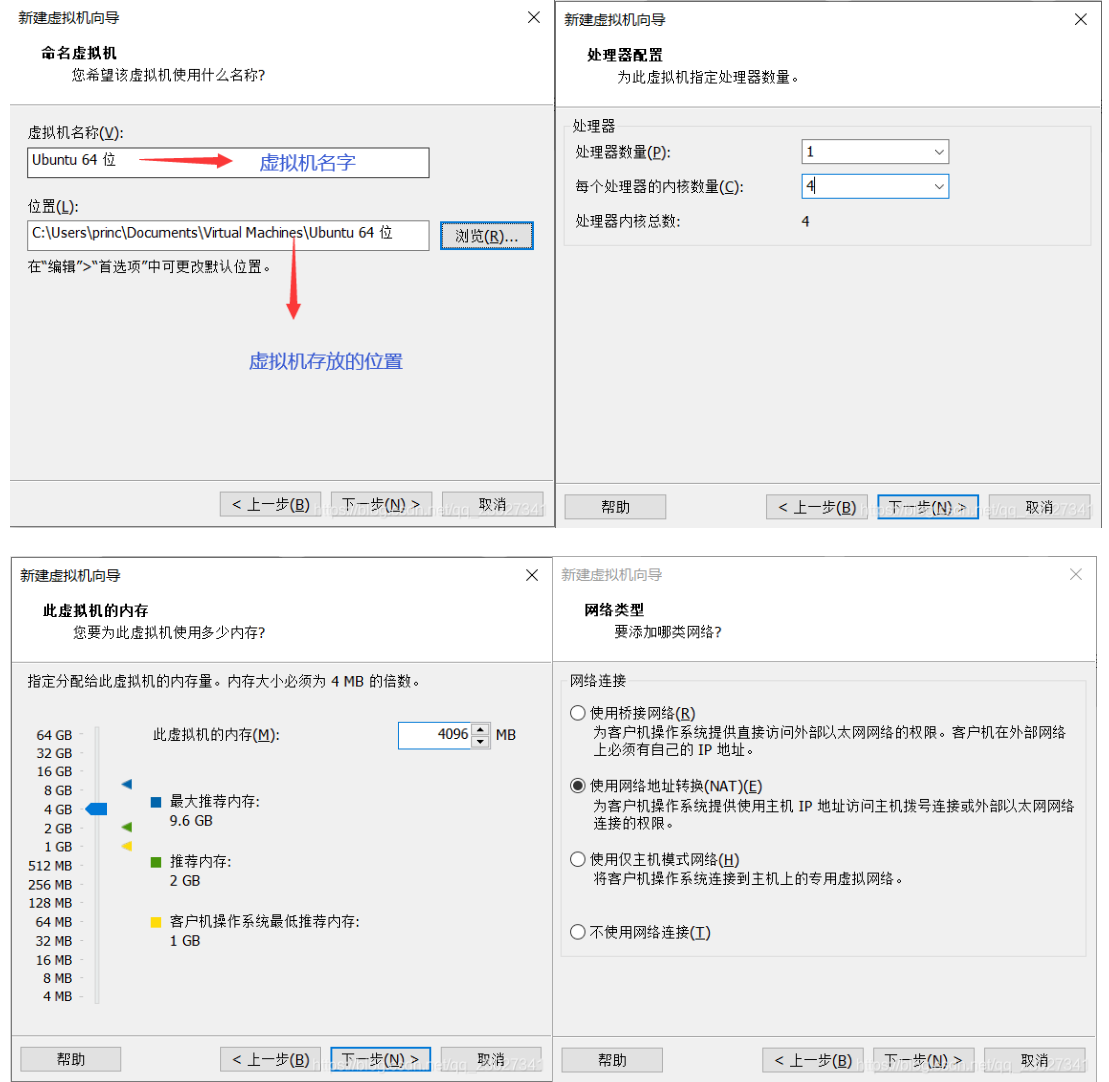
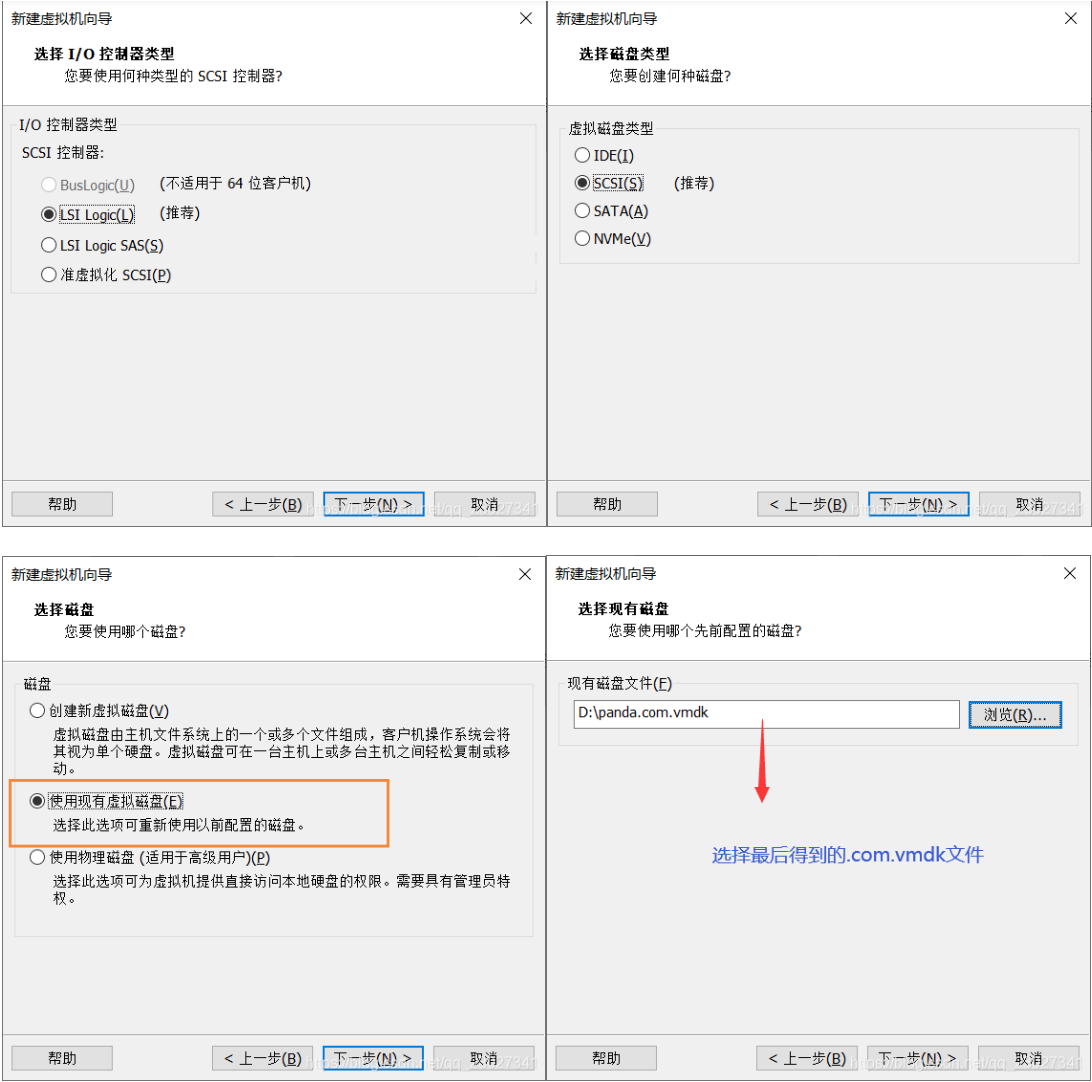
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
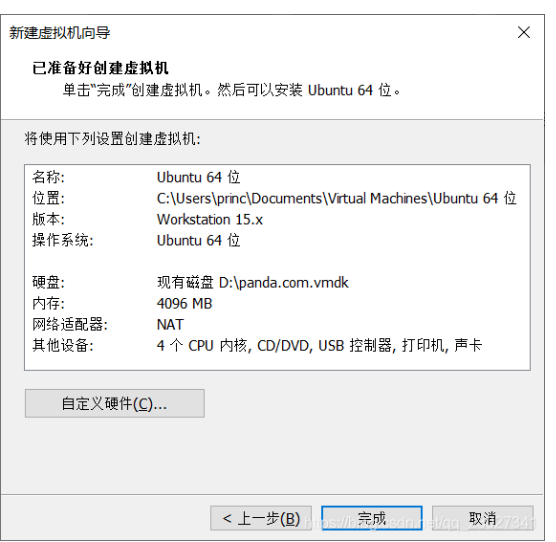
正常打开即可

相关文章：

如何将VirtualBox虚拟机转换到VMware中

转换前的准备 首先需要你找到你的virtualbox以及VM安装到哪个文件夹里了，需要将这两个文件夹添加进环境变量Path中。 如果你记不清了，可以用everything全局搜索一下“VBoxManage.exe’以及“vmware-vdiskmanager.exe”，看一眼这个程序放到哪…...

编程日记 2023/5/31 2:14:48

洞庭龙梦（开发技巧和结构理论集）

1、经验来源，单一获取方式。进行形态等级展示。唯一游戏系统经验来源。无主线和支线剧情。2、玩家使用流通货币（充值货币），到玩家空间商城充值游戏，两人以上玩家进行游戏，掉落道具。交易系统游戏玩法&#…...

编程日记 2023/5/25 19:04:38

【23种设计模式】创建型模式详细介绍

前言 本文为 【23种设计模式】创建型模式详细介绍 相关内容介绍，下边具体将对单例模式，工厂方法模式，抽象工厂模式，建造者模式，原型模式，具体包括它们的特点与实现等进行详尽介绍~ 📌博主主页&…...

编程日记 2023/5/31 2:14:48

@Bean的处理流程，源码分析@Bean背后发生的事

文章目录写在前面关键类ConfigurationClassPostProcessor1、ConfigurationClassPostProcessor的注册2、ConfigurationClassPostProcessor的处理过程（1）parse方法中，Bean方法的处理（2）注册解析Bean标注的方法写在前面 …...

编程日记 2023/5/24 14:17:51

css实现圆环展示百分比，根据值动态展示所占比例

代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

编程新知 2026/2/5 4:28:28

突破不可导策略的训练难题：零阶优化与强化学习的深度嵌合

强化学习&#xff08;Reinforcement Learning, RL&#xff09;是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程&#xff0c;然后使用强化学习的Actor-Critic机制&#xff08;中文译作“知行互动”机制&#xff09;&#xff0c;逐步迭代求解…...

编程新知 2026/2/5 4:17:42

3.3.1_1 检错编码（奇偶校验码）

从这节课开始&#xff0c;我们会探讨数据链路层的差错控制功能&#xff0c;差错控制功能的主要目标是要发现并且解决一个帧内部的位错误&#xff0c;我们需要使用特殊的编码技术去发现帧内部的位错误&#xff0c;当我们发现位错误之后&#xff0c;通常来说有两种解决方案。第一…...

编程新知 2026/1/30 3:28:14

大数据零基础学习day1之环境准备和大数据初步理解

学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 &#xff08;1&#xff09;设置网关 打开VMware虚拟机&#xff0c;点击编辑…...

编程新知 2026/1/25 14:43:07

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序

一、开发准备 ​​环境搭建​​&#xff1a; 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 ​​项目创建​​&#xff1a; File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

编程新知 2025/9/5 12:16:40

Nuxt.js 中的路由配置详解

Nuxt.js 通过其内置的路由系统简化了应用的路由配置&#xff0c;使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

编程新知 2026/2/6 16:52:42

CocosCreator 之 JavaScript/TypeScript和Java的相互交互

引擎版本&#xff1a; 3.8.1 语言&#xff1a; JavaScript/TypeScript、C、Java 环境&#xff1a;Window 参考&#xff1a;Java原生反射机制 您好&#xff0c;我是鹤九日&#xff01; 回顾 在上篇文章中&#xff1a;CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

编程新知 2026/1/30 12:10:19

反射获取方法和属性

Java反射获取方法 在Java中&#xff0c;反射&#xff08;Reflection&#xff09;是一种强大的机制&#xff0c;允许程序在运行时访问和操作类的内部属性和方法。通过反射&#xff0c;可以动态地创建对象、调用方法、改变属性值&#xff0c;这在很多Java框架中如Spring和Hiberna…...

编程新知 2025/11/9 2:57:17

令牌桶 滑动窗口-＞限流 分布式信号量-＞限并发的原理 lua脚本分析介绍

文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结&#xff1a; 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析&#xff1a; 实际业务去理解体会统一注…...

编程新知 2026/1/29 16:36:27

WEB3全栈开发——面试专业技能点P2智能合约开发（Solidity）

一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解&#xff0c;适合用作学习或写简历项目背景说明。 &#x1f9e0; 一、概念简介&#xff1a;Solidity 合约开发 Solidity 是一种专门为 以太坊&#xff08;Ethereum&#xff09;平台编写智能合约的高级编…...

编程新知 2026/1/27 9:33:09