力扣 hot100 -- 多维动态规划
👇woc,这不是最熟悉那种,记忆化 dfs 或者 普通的深度优先搜索??都适用于二维地图👇
DFS(深度优先搜索)8种题型_dfs典型问题-CSDN博客
目录
🥃不同路径
🌼最小路径和
🌼最长回文子串
AC 中心扩散
AC 动态规划
🐙最长公共子序列
🎂编辑距离
🥃不同路径
62. 不同路径 - 力扣(LeetCode)
“只能向下 或 向右”(注意限制条件)
注意二维vector的初始化,也可以直接用数组
/*
dp[i][j] : 到达(i, j)的路径数
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 每个点只来自于上边和左边
初始化 : dp[i][0] = 1, dp[][j] = 1
*/
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m, vector<int>(n, 0)); // m行, 每一行 n 个元素for (int j = 0; j < n; ++j) dp[0][j] = 1; // 第一行初始化for (int i = 0; i < m; ++i)dp[i][0] = 1; // 第一列初始化for (int i = 1; i < m; ++i)for (int j = 1; j < n; ++j) dp[i][j] = dp[i - 1][j] + dp[i][j - 1];return dp[m-1][n-1];}
};🌼最小路径和
64. 最小路径和 - 力扣(LeetCode)
“只能向下 或 向右”(注意限制条件)
和上一题初始化不同,上一条是不同路径,本题是最小路径和
/*
dp[i][j] : 到达(i, j)的最小路径和
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]
初始化 : dp[0][0], 然后从 (0,0) 开始,分别向右向下初始化第 0 行,第 0 列
*/
class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();vector<vector<int>> dp(m, vector<int>(n, 0));dp[0][0] = grid[0][0];for (int j = 1; j < n; ++j)dp[0][j] = dp[0][j - 1] + grid[0][j]; // 第 0 行for (int i = 1; i < m; ++i)dp[i][0] = dp[i - 1][0] + grid[i][0]; // 第 0 列for (int i = 1; i < m; ++i)for (int j = 1; j < n; ++j) {dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];}return dp[m-1][n-1];}
};🌼最长回文子串
5. 最长回文子串 - 力扣(LeetCode)
AC 中心扩散
遍历每一个字母,以这个字母为中心往外扩散,先找到以此为中心全部相同的字母
(比如 acdbbd 中的 bb),然后同时开始左右扩散,l - 1, r + 1,直到遇到左右边界不相等的字母(d == d,后面就不相等了,所以最长回文子串是 dbbd)
时间 O(n^2)
class Solution {
public:string longestPalindrome(string s) {int l = 0, r = 0, maxLen = 1; // 初始化 l, r 防止一个元素 out of rangefor (int i = 0; i < s.size(); ++i) {int left = i - 1, right = i + 1, len = 1; // len 当前长度// 左边 == s[i] 的while (left >= 0 && s[left] == s[i]) {left--;len++; }// 右边 == s[i] 的while (right < s.size() & s[right] == s[i]) {right++;len++;}// 左右同时扩展while (left >= 0 && right < s.size() && s[left] == s[right]) left--, right++, len += 2;if (len > maxLen) {maxLen = len;l = left + 1, r = right - 1; // 最长子串区间 [l, r]}}return s.substr(l, r - l + 1);}
};AC 动态规划
中心扩散会有大量重复计算,比如 abbacd,第一个 b 已经计算过的回文串,第二个 b 还会重新计算,而 dp 能将计算过的状态记住,个别情况接近 O(n)
代码写完后,貌似没有发现时间上的优化,似乎都是差不多的
时间 O(n^2)
/*
dp[i][j] : 子串 [i, j] 区间是否回文
dp[i][j] = (dp[i+1][j-1] || j - i == 1) && (s[i] == s[j])
初始化 : dp[i][i] = 1
*/
class Solution {
public:string longestPalindrome(string s) {int maxLen = 1, l = 0, r = 0, n = s.size();// 记得初始化 vector, 正确分配内存, 不然报错 null pointervector<vector<int>> dp(n, vector<int>(n, 0));for (int i = 0; i < n; ++i)dp[i][i] = 1;for (int j = 1; j < n; ++j) // 右边界 jfor (int i = 0; i < j; ++i) // 左边界 iif (s[i] == s[j] && (dp[i + 1][j - 1] || j - i == 1)) {dp[i][j] = 1;if (j - i + 1 > maxLen)maxLen = j - i + 1, l = i, r = j;}return s.substr(l, r - l + 1);}
};🐙最长公共子序列
1143. 最长公共子序列 - 力扣(LeetCode)
dp[][] 下标从 1 开始,就不用初始化那么麻烦,也就是 dp[1][1] = 1,表示 text1[0] == text2[0]
/*
dp[i][j] : s1的[0, i-1] 和 s2的[0, j-1] 的最长公共子序列
if (s1[i-1] == s2[j-1]) dp[i][j] = dp[i-1][j-1] + 1
else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
初始化 : dp[0][0] = 0 OR 1
*/
class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int m = text1.size(), n = text2.size();vector<vector<int>> dp(m+1, vector<int>(n+1, 0));for (int i = 1; i <= m; ++i) // dp[][] 下标从 1 开始for (int j = 1; j <= n; ++j) {if (text1[i-1] == text2[j-1])dp[i][j] = dp[i-1][j-1] + 1;elsedp[i][j] = max(dp[i-1][j], dp[i][j-1]);}return dp[m][n];}
};// a c b q d b b q
// a c d q🎂编辑距离
72. 编辑距离 - 力扣(LeetCode)
1)类似上一题,dp[][] 下标从 1 开始,避免了麻烦的初始化,因为递推式有 [i-1][j-1], [i][j-1],
[i-1][j] 三种组合(下标改 1 开始后,<= m <= n)
2)增删改的递推式中,+1不一定正确,所以要取 增 删 改 的最小值
3)初始化,观察递推式,都是根据 左,上,左上 三个方位得到的,所以初始化第一行和第一列
/*
dp[i][j] : s1 前 i 个字符 --> s2 前 j 个字符(下标 1 开始)递推式: dp[i][j] = ...
(取增删改,三者的最小值,作为新的 dp[i][j])s1 增加1个变 s2: dp[i][j-1] + 1
s1 删除1个变 s2: dp[i-1][j] + 1
s1 替换1个变 s2: dp[i-1][j-1] + 1if (s1[i] == s2[j]) dp[i-1][j-1]
*/
class Solution {
public:int minDistance(string word1, string word2) {int m = word1.size(), n = word2.size();vector<vector<int>> dp(m+1, vector<int>(n+1, 0));// 初始化for (int i = 1; i <= m; ++i)dp[i][0] = i; // 第一列for (int j = 1; j <= n; ++j)dp[0][j] = j; // 第一行for (int i = 1; i <= m; ++i)for (int j = 1; j <= n; ++j) {if (word1[i-1] == word2[j-1])dp[i][j] = dp[i - 1][j - 1]; // 不用操作else // 增删改的最小值dp[i][j] = min(dp[i][j-1], min(dp[i-1][j], dp[i-1][j-1])) + 1;}return dp[m][n];}
};相关文章:

力扣 hot100 -- 多维动态规划
👇woc,这不是最熟悉那种,记忆化 dfs 或者 普通的深度优先搜索??都适用于二维地图👇 DFS(深度优先搜索)8种题型_dfs典型问题-CSDN博客 目录 🥃不同路径 🌼最…...

[misc]-流量包-wireshark-icmp
wireshark打开,大部分都是icmp,查看data部分 提取data长度: tshark.exe -r 1.pcapng -T fields -e data.len > length.txt 使用python解析这个文件,剔除异常值,每8个取一个值,得到flag ds [] with open(length.tx…...

探索性数据分析:使用Python与Pandas库实现数据洞察
探索性数据分析:使用Python与Pandas库实现数据洞察 引言 在当今数据驱动的时代,数据分析已成为决策制定、策略规划和业务优化的关键环节。无论是商业智能、金融分析还是市场研究,数据分析都扮演着至关重要的角色。Pandas库作为Python生态系统…...

枚举的高阶用法之枚举里写方法以及注入spring的bean
1、前言 一般我们使用枚举都是用来定义一些常量。比如我们需要一个表示订单类(pc订单、手机订单)的常量,那我们就可以使用枚举来实现,如下: AllArgsConstructor public enum OrderTypeEnum{PC("PC", "电脑端"),PHONE("PHONE", "手机端&quo…...

游戏开发面试题2
网络游戏分为客户端和服务端,你能说说客户端和服务端都干了一些什么工作吗? 客户端(Client) 客户端是玩家直接交互的部分,主要负责用户界面、输入处理、渲染和部分逻辑处理。具体工作包括: 用户界面&…...

华为机试题-单车道汽车通行时间-Java
代码在最后面 1 题目描述 M(1 ≤ M ≤ 20)辆车需要在一条不能超车的单行道到达终点,起点到终点的距离为 N(1 ≤ N ≤ 400)。 速度快的车追上前车后,只能以前车的速度继续行驶,求最后一辆车到达…...

6-5,web3浏览器链接区块链(react+区块链实战)
6-5,web3浏览器链接区块链(react区块链实战) 6-5 web3浏览器链接区块链(调用读写合约与metamask联动) 6-5 web3浏览器链接区块链(调用读写合约与metamask联动) 这里就是浏览器端和智能合约的交…...

C# 多态性
C# 多态性 介绍 多态性是面向对象编程(OOP)的一个核心概念,它允许不同类的对象对同一消息做出响应,并产生不同的结果。在C#中,多态性主要通过继承、接口和虚方法来实现。本文将深入探讨C#中的多态性,包括其原理、实现方式以及在实际编程中的应用。 原理 多态性允许将…...

Visual Studio 安装程序无法执行修复或更新
一.问题场景 出现问题的场景:当你的VS已经安装但是无法在工具中下载新组件或者卸载了当时一直无法安装。 二.问题原因 如果计算机上的 Visual Studio 实例已损坏,则可能会出现此问题。 三.解决方法 如果之前尝试修复或更新 Visual Studio 失败&…...
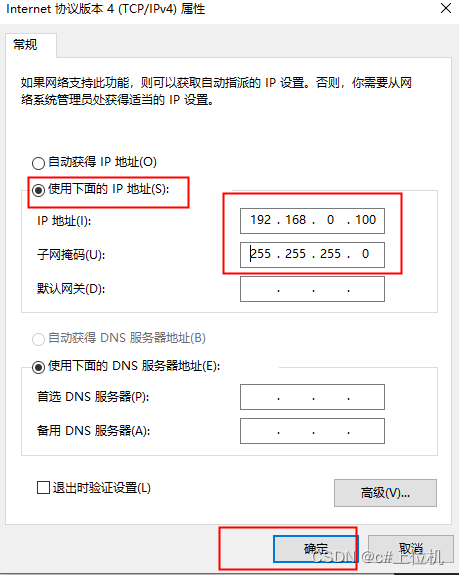
C#与PLC通信——如何设置电脑IP地址
前言: 我们与PLC通过以太网通信时,首先要做的就是先设置好电脑的IP,这样才能实现上位机电脑与PLC之间的通信,并且电脑的ip地址和PLC的Ip地址要同处于一个网段,比如电脑的Ip地址为192.168.1.1,那么PLC的Ip地…...

Milvus 核心设计(1) ---- 数据一致性的等级及使用场景
目录 背景 Milvus的数据一致性 设置数据一致性等级 等级类型 PACELC定理 level 详细解释 Strong Bounded staleness Session Eventually 总结 背景 分布式上的可扩展性是个比较重要的concept。Chroma 核心之前写过了,他的最大优势在于轻量级且好用。Milvus相对Ch…...
EasyCVR视频技术:城市电力抢险的“千里眼”,助力抢险可视化
随着城市化进程的加速和电力需求的不断增长,电力系统的稳定运行对于城市的正常运转至关重要。然而,自然灾害、设备故障等因素常常导致电力中断,给城市居民的生活和企业的生产带来严重影响。在这种情况下,快速、高效的电力抢险工作…...

【Wamp】局域网设备访问WampServer | 使用域名访问Wamp | Wamp配置HTTPS
局域网设备访问WampServer 参考:https://www.jianshu.com/p/d431a845e5cb 修改Apache的httpd.conf文件 D:\Academic\Wamp\program\bin\apache\apache2.4.54.2\conf\httpd.conf 搜索 Require local 和Require all denied,改为Require all granted <…...

采用自动微分进行模型的训练
自动微分训练模型 简单代码实现: import torch import torch.nn as nn import torch.optim as optim# 定义一个简单的线性回归模型 class LinearRegression(nn.Module):def __init__(self):super(LinearRegression, self).__init__()self.linear nn.Linear(1, 1) …...

k8s怎么配置secret呢?
在Kubernetes中,配置Secret主要涉及到创建、查看和使用Secret的过程。以下是配置Secret的详细步骤和相关信息: ### 1. Secret的概念 * Secret是Kubernetes用来保存密码、token、密钥等敏感数据的资源对象。 * 这些敏感数据可以存放在Pod或镜像中&#x…...

算法篇 滑动窗口 leetcode 长度最小的子数组
长度最小的子数组 1. 题目描述2. 算法图分析2.1 暴力图解2.2 滑动窗口图解 3. 代码演示 1. 题目描述 2. 算法图分析 2.1 暴力图解 2.2 滑动窗口图解 3. 代码演示...

数据库作业d8
要求: 一备份 1 mysqldump -u root -p booksDB > booksDB_all_tables.sql 2 mysqldump -u root -p booksDB books > booksDB_books_table.sql 3 mysqldump -u root -p --databases booksDB test > booksDB_and_test_databases.sql 4 mysql -u roo…...
前后端数据交互设计到的跨域问题
前后端分离项目的跨域问题及解决办法 一、跨域简述 1、问题描述 这里前端vue项目的端口号为9000,后端springboot项目的端口号为8080 2、什么是跨域 当一个请求url的协议、域名、端口三者之间任意一个与当前页面url不同即为跨域 当前页面url被请求页面url是否…...

非洲猪瘟监测设备的作用是什么?
TH-H160非洲猪瘟监测设备的主要作用是迅速、准确地检测出非洲猪瘟病毒,从而帮助控制和预防疫情的扩散。这些设备利用先进的生物传感技术和PCR分子生物学方法,能够在极短的时间内提供精确的检测结果<sup>1</sup><sup>2</sup><…...

移动硬盘损坏无法读取?专业恢复策略全解析
在数字化信息爆炸的今天,移动硬盘作为我们存储和传输大量数据的重要工具,其安全性和稳定性直接关系到个人与企业的数据安全。然而,当移动硬盘突然遭遇损坏,无法正常读取时,我们该如何应对?本文将深入探讨移…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...
