Milvus 核心设计(1) ---- 数据一致性的等级及使用场景
目录
背景
Milvus的数据一致性
设置数据一致性等级
等级类型
PACELC定理
level 详细解释
Strong
Bounded staleness
Session
Eventually
总结
背景
分布式上的可扩展性是个比较重要的concept。Chroma 核心之前写过了,他的最大优势在于轻量级且好用。Milvus相对Chroma 来说,安装和API 调用都相对复杂一些。当然Milvus的核心组件目前来看要丰富一些,包括了Kafka,Pluster,RocketMQ等消息队列,也包含etcd,mysql 等可选组件。但无论怎样,是应用场景的不同,没有谁比谁更好,只是根据场景选适合的container 罢了。在分布式系统上,比较重要的是数据一致性问题,今天主要focus 这个讲下。
Milvus的数据一致性
设置数据一致性等级

等级类型

PACELC定理
PACELC定理(Partition tolerance, Availability, Consistency, Latency, and Consistency and Latency)确实揭示了分布式系统中一些关键属性之间的权衡关系。PACELC定理指出,在存在网络分区(Partition tolerance)的情况下,系统必须在可用性(Availability)和一致性(Consistency)之间做出选择,而这通常会影响系统的延迟(Latency)。此外,它还表明,如果系统选择了一致性(Consistency)而不是可用性(Availability),那么延迟(Latency)可能会增加;相反,如果系统选择了可用性(Availability),那么它可能只能达到最终一致性(Eventually Consistency),但延迟(Latency)会降低。
level 详细
相关文章:

Milvus 核心设计(1) ---- 数据一致性的等级及使用场景
目录 背景 Milvus的数据一致性 设置数据一致性等级 等级类型 PACELC定理 level 详细解释 Strong Bounded staleness Session Eventually 总结 背景 分布式上的可扩展性是个比较重要的concept。Chroma 核心之前写过了,他的最大优势在于轻量级且好用。Milvus相对Ch…...
EasyCVR视频技术:城市电力抢险的“千里眼”,助力抢险可视化
随着城市化进程的加速和电力需求的不断增长,电力系统的稳定运行对于城市的正常运转至关重要。然而,自然灾害、设备故障等因素常常导致电力中断,给城市居民的生活和企业的生产带来严重影响。在这种情况下,快速、高效的电力抢险工作…...

【Wamp】局域网设备访问WampServer | 使用域名访问Wamp | Wamp配置HTTPS
局域网设备访问WampServer 参考:https://www.jianshu.com/p/d431a845e5cb 修改Apache的httpd.conf文件 D:\Academic\Wamp\program\bin\apache\apache2.4.54.2\conf\httpd.conf 搜索 Require local 和Require all denied,改为Require all granted <…...

采用自动微分进行模型的训练
自动微分训练模型 简单代码实现: import torch import torch.nn as nn import torch.optim as optim# 定义一个简单的线性回归模型 class LinearRegression(nn.Module):def __init__(self):super(LinearRegression, self).__init__()self.linear nn.Linear(1, 1) …...

k8s怎么配置secret呢?
在Kubernetes中,配置Secret主要涉及到创建、查看和使用Secret的过程。以下是配置Secret的详细步骤和相关信息: ### 1. Secret的概念 * Secret是Kubernetes用来保存密码、token、密钥等敏感数据的资源对象。 * 这些敏感数据可以存放在Pod或镜像中&#x…...

算法篇 滑动窗口 leetcode 长度最小的子数组
长度最小的子数组 1. 题目描述2. 算法图分析2.1 暴力图解2.2 滑动窗口图解 3. 代码演示 1. 题目描述 2. 算法图分析 2.1 暴力图解 2.2 滑动窗口图解 3. 代码演示...

数据库作业d8
要求: 一备份 1 mysqldump -u root -p booksDB > booksDB_all_tables.sql 2 mysqldump -u root -p booksDB books > booksDB_books_table.sql 3 mysqldump -u root -p --databases booksDB test > booksDB_and_test_databases.sql 4 mysql -u roo…...
前后端数据交互设计到的跨域问题
前后端分离项目的跨域问题及解决办法 一、跨域简述 1、问题描述 这里前端vue项目的端口号为9000,后端springboot项目的端口号为8080 2、什么是跨域 当一个请求url的协议、域名、端口三者之间任意一个与当前页面url不同即为跨域 当前页面url被请求页面url是否…...

非洲猪瘟监测设备的作用是什么?
TH-H160非洲猪瘟监测设备的主要作用是迅速、准确地检测出非洲猪瘟病毒,从而帮助控制和预防疫情的扩散。这些设备利用先进的生物传感技术和PCR分子生物学方法,能够在极短的时间内提供精确的检测结果<sup>1</sup><sup>2</sup><…...

移动硬盘损坏无法读取?专业恢复策略全解析
在数字化信息爆炸的今天,移动硬盘作为我们存储和传输大量数据的重要工具,其安全性和稳定性直接关系到个人与企业的数据安全。然而,当移动硬盘突然遭遇损坏,无法正常读取时,我们该如何应对?本文将深入探讨移…...

神经网络以及简单的神经网络模型实现
神经网络基本概念: 神经元(Neuron): 神经网络的基本单元,接收输入,应用权重并通过激活函数生成输出。 层(Layer): 神经网络由多层神经元组成。常见的层包括输入层、隐藏层…...
)
java中压缩文件的解析方式(解析文件)
背景了解:java中存在IO流的方式,支持我们对文件进行读取(Input,从磁盘到内存)或写入(output,从内存到磁盘),那么我们在面对 “zip”格式或者 “rar” 格式的压缩文件&…...

巧用 VScode 网页版 IDE 搭建个人笔记知识库!
[ 知识是人生的灯塔,只有不断学习,才能照亮前行的道路 ] 巧用 VScode 网页版 IDE 搭建个人笔记知识库! 描述:最近自己在腾讯云轻量云服务器中部署了一个使用在线 VScode 搭建部署的个人Markdown在线笔记,考虑到在线 VScode 支持终…...

Jupyter Lab 使用
Jupyter Lab 使用详解 Jupyter Lab 是一个基于 Web 的交互式开发环境,提供了比 Jupyter Notebook 更加灵活和强大的用户界面和功能。以下是使用 Jupyter Lab 的详细指南,包括安装、基本使用、设置根目录和扩展功能等内容。 一、Jupyter Lab 安装与启动…...
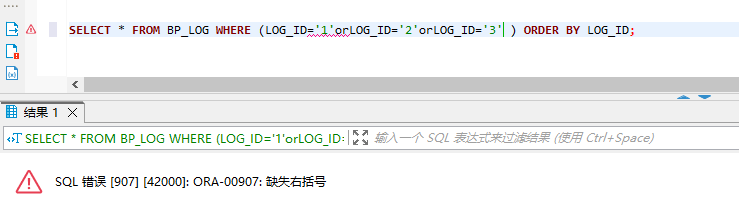
MyBatis where标签内嵌foreach标签查询报错‘缺失右括号‘或‘命令未正确结束‘
MyBatis <where>标签内嵌<foreach>标签查询报错’缺失右括号’或’命令未正确结束’ <where>标签内嵌<foreach>标签 截取一段脱敏xml,写明大概意思 <select id"queryLogByIds" resultMap"BaseResultMap">SELE…...

重生奇迹MU 群战王牌
圣导师是重生奇迹MU游戏中八大职业之一,拥有风度翩翩、潇洒自如的形象和神一样的实力。无论是刷怪、PK、打boss还是混战,圣导师都表现出压制其他职业的强大气势。因此,这个职业在游戏中备受欢迎,人气非常高。 实力强大的二代隐藏…...

SpinalHDL之VHDL 和 Verilog 生成
本文作为SpinalHDL学习笔记第十六篇,记录使用SpinalHDL代码生成Verilog/VHDL代码的方法。 SpinalHDL学习笔记总纲链接如下: SpinalHDL 学习笔记_spinalhdl blackbox-CSDN博客 目录: 1.从 SpinalHDL 组件生成 VHDL 和 Verilog 2.生成的 VHD…...

c语言中的字符串函数
strstr函数 函数介绍 strstr 用于在一个字符串中查找另一个字符串的首次出现。 我们来看这个函数的参数名字:haysytack(干草堆)needle(针),这个其实就是外国的一句谚语:在干草堆中找一根针,就…...

[AI 大模型] 百度 文心一言
文章目录 [AI 大模型] 百度 文心一言简介模型架构发展新技术和优势API 代码示例 [AI 大模型] 百度 文心一言 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0DwAIh0T-1720667576892)(https://i-blog.csdnimg.cn/direct/283919e5d78b4951ba1ade5dcfc…...

机器学习开源分子生成系列(2)-基于三维形状和静电相似性的DeepFMPO v3D安装及使用
前言 本文是基于 3D 的分子生成方法DeepFMPO v3D的介绍及安装使用。 一、DeepFMPO v3D是什么? github代码介绍文章 在药物发现中,如何寻找具新颖性和结构多样性的候选分子是颇受药物设计科学家关注的问题。通过虚拟筛选的化学空间搜索往往会受限于筛选…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
