YOLO--置信度(超详细解读)
YOLO(You Only Look Once)算法中的置信度(Confidence)是一个关键概念,用于评估模型对预测框内存在目标对象的信心程度以及预测框对目标对象位置的准确性。
一、置信度的定义
- 数值范围:置信度是一个介于0和1之间的数值。
- 意义:它表示模型对预测框内存在目标对象的确信程度。如果置信度接近1,表示模型非常确信预测框内包含了目标对象;如果置信度接近0,则表示模型认为预测框内可能不包含目标对象。

示例
假设我们有一个图像,其中包含了一个人和一个狗。我们使用YOLO算法对这个图像进行目标检测,算法输出了两个预测框,分别对应人和狗的位置。对于每个预测框,YOLO都会给出一个置信度分数。
1.预测框1:
在这个例子中,置信度0.95表示YOLO模型非常确信预测框1内存在一个目标对象(即人),并且预测框的位置也比较准确。
- 位置:图像中的某个区域,该区域包含了人的大部分身体。
- 置信度:0.95
- 类别概率:人 = 0.98(假设YOLO还输出了该预测框内对象属于各个类别的概率)
2.预测框2:
在这个例子中,置信度0.5表示YOLO模型对预测框2内存在目标对象(即狗)的信心相对较低。这可能是因为预测框只包含了狗的一部分身体,或者与其他非目标区域有所重叠,导致模型对预测结果的信心下降。
- 位置:图像中的另一个区域,该区域只包含了狗的一部分身体,并且与其他非目标区域有所重叠。
- 置信度:0.5
- 类别概率:狗 = 0.7(同样假设YOLO输出了类别概率)
二、置信度的计算
在YOLO算法中,置信度的计算通常涉及两个主要因素:
1.对象存在的概率(Objectness):这是模型预测出的一个概率值,表示预测框内存在目标对象的概率。这个概率是通过网络学习得到的,通常与预测框内的特征相关。
2.预测框与真实框的交并比(IoU):IoU是衡量预测框与真实框重叠程度的指标。在训练过程中,真实框的标注信息是已知的,因此可以计算出预测框与真实框的IoU。然而,在推理(测试)阶段,真实框是未知的,因此通常使用预测框与所有可能真实框(在假设存在的情况下)的最大IoU来估计。
IOU:

在YOLO中,置信度是通过将对象存在的概率与预测框和真实框的最高IoU(如果有一个真实框与该预测框匹配)相乘来计算的。然而,在训练过程中,由于没有真实的IoU值(因为我们在训练时需要预测它),所以通常将置信度简化为对象存在的概率。在推理(测试)时,我们会使用预测的对象存在概率和预测的框与所有真实框的IoU中的最大值(如果存在匹配的真实框)来计算置信度。
置信度的计算公式(在推理时):
其中,P(Object) 是预测框内存在对象的概率,IoU(pred,gt) 是预测框与所有真实框之间的最大IoU值(如果存在真实框与预测框匹配)。
三、置信度的作用
1.筛选预测结果:在推理阶段,通过设定置信度阈值可以过滤掉那些模型不太确信的预测结果,从而提高目标检测的准确性。
2.评估模型性能:置信度还可以作为评估模型性能的一个指标。通过比较模型在不同数据集上的置信度分布和准确性,可以了解模型的泛化能力和鲁棒性。
在实际应用中,我们可以根据置信度来筛选预测结果。例如,我们可以设置一个置信度阈值(如0.6),只有当预测框的置信度高于这个阈值时,我们才认为该预测框是有效的,并将其作为最终的检测结果输出。这样可以减少误检和漏检的情况,提高目标检测的准确性。
相关文章:
YOLO--置信度(超详细解读)
YOLO(You Only Look Once)算法中的置信度(Confidence)是一个关键概念,用于评估模型对预测框内存在目标对象的信心程度以及预测框对目标对象位置的准确性。 一、置信度的定义 数值范围:置信度是一个介于0和…...

“解锁物流新纪元:深入探索‘沂路畅通‘分布式协作平台“
"解锁物流新纪元:深入探索沂路畅通分布式协作平台" 在21世纪的数字浪潮中,物流行业作为连接生产与消费的关键纽带,其重要性不言而喻。然而,随着市场规模的持续扩大和消费者需求的日益多样化,传统物流模式已…...

昇思25天学习打卡营第六天|应用实践/计算机视觉/Vision Transformer图像分类
心得 运行模型似乎有点靠天意?每次跑模型之前先来个焚香沐浴?总之今天是机器视觉的最后一课了,尽管课程里强调模型跑得慢,可是我的这次运行,居然很快的就看到结果了。 如果一直看我这个系列文章的小伙伴,…...

vxe-table合并行数据
场景: 混批名称相同合并混批名称,在混批名称相同条件下合并相同的混批类型;在混混批类型相同条件下合并相同的混批值;在混批值相同条件下合并相同的单位 实现根据四个不同的key值,当四个key值对应相等时,合…...
LabVIEW异步和同步通信详细分析及比较
1. 基本原理 异步通信: 原理:异步通信(Asynchronous Communication)是一种数据传输方式,其中数据发送和接收操作在独立的时间进行,不需要在特定时刻对齐。发送方在任何时刻可以发送数据,而接收…...

【多模态学习笔记二】MINIGPT-4论文阅读
MINIGPT-4:ENHANCING VISION-LANGUAGE UNDERSTANDING WITH ADVANCED LARGE LANGUAGE MODELS 提出的MiniGPT-4使用一个投影层,将冻结的视觉编码器与冻结的先进的LLM Vicuna对齐。我们的工作首次揭示,将视觉特征与先进的大型语言模型正确对齐可以具有GPT-4所展示的许多先进的多…...
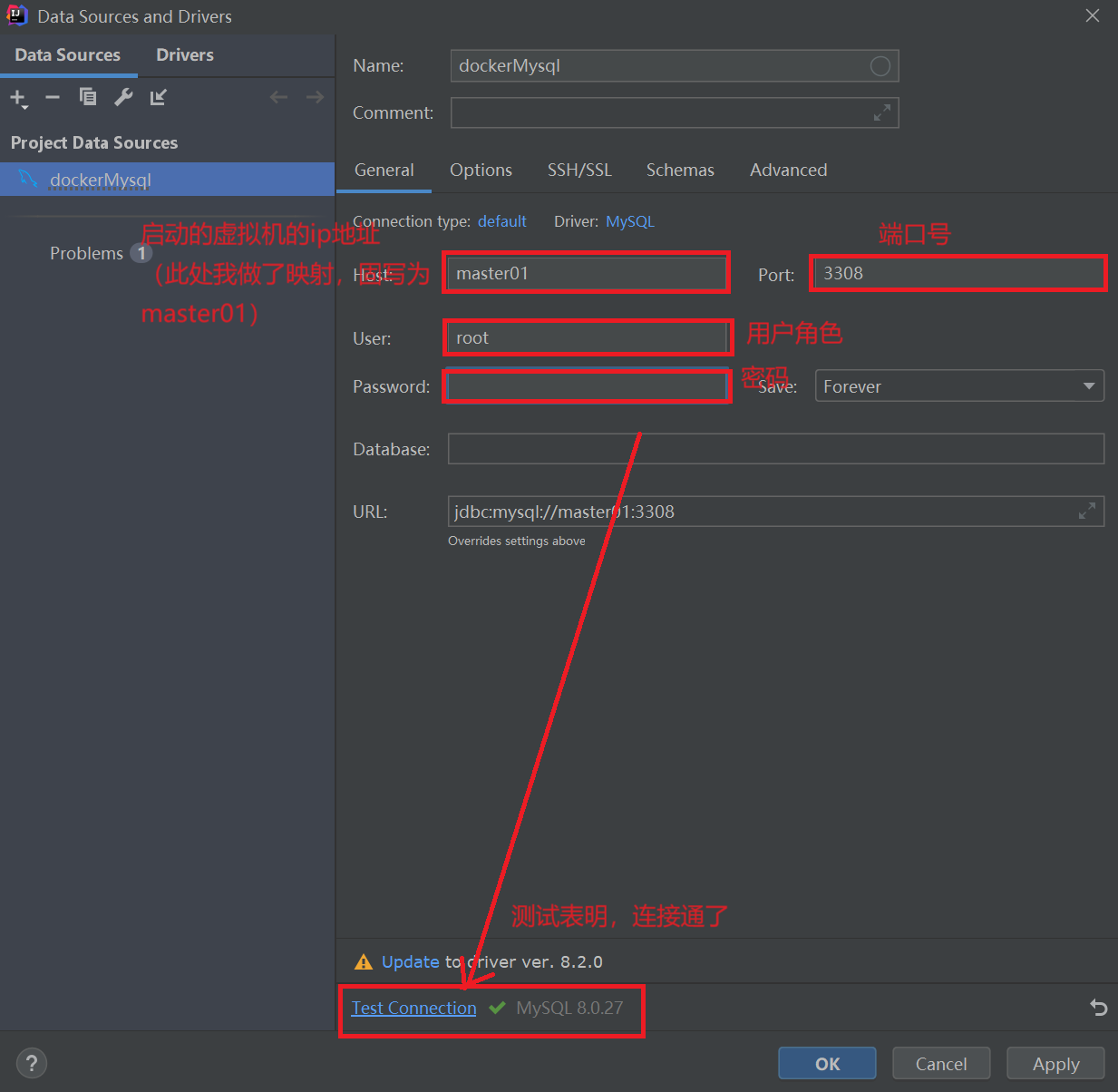
Docker基本讲解及演示
Docker安装教程 Docker安装教程 1、Docker介绍 Docker是一个开源的应用容器引擎,允许开发者将应用程序及其依赖项打包成一个轻量级、可移植的容器,然后发布到任何支持 Docker 的环境中运行,无论是开发机、测试机还是生产环境。 Docker基于…...

各类专业技术的pdf电子书
从业多年,收集了海量的pdf电子书籍,感兴趣的私聊。...

【Linux】多线程_9
文章目录 九、多线程10. 线程池 未完待续 九、多线程 10. 线程池 这里我没实现一些 懒汉单例模式 的线程池,并且包含 日志打印 的线程池: Makefile: threadpool:Main.ccg -o $ $^ -stdc11 -lpthread .PHONY:clean clean:rm -f threadpoolT…...

LabVIEW设备检修信息管理系统
开发了基于LabVIEW设计平台开发的设备检修信息管理系统。该系统应用于各种设备的检修基地,通过与基地管理信息系统的连接和数据交换,实现了本地检修工位数据的远程自动化管理,提高了设备的检修效率和安全性。 项目背景 现代设备运维过程中信…...

python爬虫基础:使用lxml库进行HTML解析和数据提取的实践指南
使用lxml库进行HTML解析和数据提取的实践指南 在Python编程中,网页抓取和数据提取是一项常见任务。lxml库因其高效性和强大的XPath支持,成为了处理HTML和XML文档的优选工具。本文将带你了解如何使用lxml来解析HTML文档并提取所需数据。 1. 安装lxml库 …...

大语言模型系列:Transformer
在自然语言处理(NLP)领域,Transformer模型自2017年由Vaswani等人在论文《Attention Is All You Need》中提出以来,已成为最具影响力的技术之一。这种模型设计的核心是自注意力机制,它允许模型在处理序列数据时…...

宠物健康新守护:智能听诊器引领科技突破
在宠物护理领域,一项令人瞩目的科技创新正逐渐兴起,那便是智能听诊器。这款革命性的设备以前所未有的准确性和便利性,为宠物主人提供了一种全新的健康监测体验。 只需将智能听诊器轻轻放置在爱宠的身上,它便立即开始工作…...

KITTI 3D 数据可视化
引言 KITTI 视觉基准测试套件(KITTI Vision Benchmark Suite)提供了大量用于理解自动驾驶场景的工具。尤其是3D数据可视化在分析和解释传感器(如激光雷达)与环境的复杂交互中起到了至关重要的作用。本文将详细探讨KITTI数据集中3…...

旅游数据可视化:免费工具让复杂数据变得简单易懂
随着旅游业的蓬勃发展,海量的数据如同繁星点点,记录着每一位旅者的足迹与偏好。然而,如何将这些复杂的数据转化为直观、易懂的信息,为旅游企业精准决策、为消费者提供更加个性化的服务,成为了行业内外共同关注的焦点。…...

数据结构进阶:使用链表实现栈和队列详解与示例(C, C#, C++)
文章目录 1、 栈与队列简介栈(Stack)队列(Queue) 2、使用链表实现栈C语言实现C#语言实现C语言实现 3、使用链表实现队列C语言实现C#语言实现C语言实现 4、链表实现栈和队列的性能分析时间复杂度空间复杂度性能特点与其他实现的比较…...

【线程系列之五】线程池介绍C语言
一、基本概念 1.1 概念 线程池(Thread Pool)是一种基于池化技术管理线程的机制,旨在减少线程创建和销毁的开销,提高系统资源的利用率,以及更好地控制系统中同时运行的线程数量。线程池通过预先创建一定数量的线程&am…...

【学习css3】使用flex和grid实现等高元素布局
过往的实现方法是使用浮动加计算布局来实现,当flex和grid问世时,这一切将变得简单起来 一、简单的两列实现 1、先看页面效果 2、css代码 .container {padding: 10px;width: 100ch;margin: 0 auto;box-shadow: inset 0 0 0 2px #ccc;}.column {margin: 2…...

如何防止Eclipse格式化程序在行注释开头插入空格
格式化前: //foo bar 格式化后: // foo bar 这种看着不是很舒服。如果不让格式化时自动在注释符后面插入空格呢? 要在Eclipse中进行代码格式化时防止在行注释(//)后面自动增加空格,可以通过调整…...

Nextjs 调用组件内的方法
在 Next.js 中,如果你想从一个组件外部调用组件内部的方法,可以使用 React 的 useRef 钩子来引用组件实例并调用其方法。这种方法主要适用于类组件,但也可以用于函数组件,通过将方法暴露在 ref 对象上。 以下是一个示例ÿ…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...
