最长上升子序列(LIS)
最长上升子序列(最长递增子序列,LIS)
给定长度为 n n n的序列 v v v,求此序列中严格递增(上升)的子序列长度最大值(子序列可由原序列中不连续的元素构成)
朴素DP( O ( n 2 ) O(n^2) O(n2))
闫氏DP分析法
-
状态表示:
- 集合 d p dp dp:所有满足递增条件的元素集
- 属性: M a x Max Max, d p [ i ] dp[i] dp[i]表示以 i i i结尾的最长递增子序列长度, i n i t ( d p ) = 1 init(dp)=1 init(dp)=1
-
状态计算:
- i i i为当前工作区间尾指针, j j j为当前工作区间工作指针
- i i i不可选: v [ i ] ≤ v [ j ] v[i]\le v[j] v[i]≤v[j],不满足递增条件,不选
- i i i可选: v [ i ] > v [ j ] v[i]>v[j] v[i]>v[j]
- 选 i i i: d p [ i ] dp[i] dp[i]长度继承自 d p [ j ] dp[j] dp[j], d p [ i ] = d p [ j ] + 1 dp[i]=dp[j]+1 dp[i]=dp[j]+1
- 不选 i i i:该子序列 [ [ 1 ] , [ . . . ] , [ j ] ] [[1],[...],[j]] [[1],[...],[j]]可能是一个非最优子序列或最优子序列的子序列, d p [ i ] = d p [ i ] dp[i]=dp[i] dp[i]=dp[i]
-
转移方程式: d p [ i ] = m a x ( d p [ i ] , d p [ j ] + 1 ) dp[i]=max(dp[i],dp[j]+1) dp[i]=max(dp[i],dp[j]+1)
extern vector<int>v,dp;
int lis(){fill(dp.begin(),dp.end(),1);for(int i=0;i<v.size();i++)for(int j=0;j<i;j++)if(v[i]>v[j])//v[i]可选dp[i]=max(dp[i],dp[j]+1);return *max_element(dp.begin(),dp.end());
}
贪心(O( n log 2 n n\log_2n nlog2n))
思路:设原序列 v v v,答案序列 a n s ans ans,当前工作指针为 i i i。初始化 a n s [ 0 ] = v [ 0 ] ans[0]=v[0] ans[0]=v[0],遍历原序列 v v v:
- 若 v [ i ] v[i] v[i]> a n s . b a c k ( ) ans.back() ans.back(),则将 v [ i ] v[i] v[i]加入 a n s ans ans末尾
- 否则,用 v [ i ] v[i] v[i]替换 a n s ans ans中首个 ≥ v [ i ] \ge v[i] ≥v[i]的元素。由于 a n s ans ans始终有序,故可采用二分加速
extern int n;
extern vector<int>v,ans;
void lis(){ans.push_back(v[0]);for(auto i:v){if(i>ans.back()]) ans.push_back(i);else ans[distance(ans.begin(),lower_bound(ans.begin(),ans.end(),i))]=i;}cout<<ans.size()<<endl;
}
LCS求解LIS( O ( n 2 ) O(n^2) O(n2),不常用)
思路:将原序列 v v v排序得到序列 v ′ v' v′,两序列的 L C S LCS LCS也为有序,即为原序列 v v v的 L I S LIS LIS。此方法存在缺陷,仅适用于原序列 v v v中不存在重复元素的情况,否则会出现错误。下面仅以二维 d p dp dp数组的 L C S LCS LCS举例
extern int n,v1[MAX],v2[MAX],dp[MAX][MAX];
void lcs(){for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)if(v1[i-1]==v2[j-1]) dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);cout<<dp[n][n]<<endl;
}
最长连续上升子序列
转移方程式: d p [ i ] = d p [ i − 1 ] + 1 dp[i]=dp[i-1]+1 dp[i]=dp[i−1]+1
extern vector<int>v,dp;
void lcis(){fill(dp.begin(),dp.end(),1);for(int i=1;i<v.size();i++)if(v[i]>v[i-1])dp[i]=dp[i-1]+1;return *max_element(dp.begin(),dp.end());
}
复杂度 O ( n ) O(n) O(n)
相关文章:
)
最长上升子序列(LIS)
最长上升子序列(最长递增子序列,LIS) 给定长度为 n n n的序列 v v v,求此序列中严格递增(上升)的子序列长度最大值(子序列可由原序列中不连续的元素构成) 朴素DP( O ( n 2 ) O(n^2) O(n2)) 闫氏DP分析法 状态表示: 集合 d p dp dp:所有满足…...

自动驾驶车道线检测系列—3D-LaneNet: End-to-End 3D Multiple Lane Detection
文章目录 1. 摘要概述2. 背景介绍3. 方法3.1 俯视图投影3.2 网络结构3.2.1 投影变换层3.2.2 投影变换层3.2.3 道路投影预测分支 3.3 车道预测头3.4 训练和真实值关联 4. 实验4.1 合成 3D 车道数据集4.2 真实世界 3D 车道数据集4.3 评估结果4.4 评估图像仅车道检测 5. 总结和讨论…...

手工创建 postgres kamailio 数据库
测试环境如下: postgres server 16: ip 地址为 192.168.31.100,用户 postgres 的密码为 ****** kamailio v5.7.5: ip 地址为 192.168.31.101 1.1. 创建 kamailio 用户和 kamailio 数据库 ssh 登陆 kamailio (192.168.31.101)&a…...

装饰设计模式
装饰设计模式应用在IO流上面可以得到体现 装饰模式指的是在不改变原类, 不使用继承的基础上,动态地扩展一个对象的功能。 原来的inputstream已经可以读取数据了,但是是一个字节一个字节的读取的,为了优化这个我们采用了buffered,…...

Linux 线程初步解析
1.线程概念 在一个程序里的一个执行路线就叫做线程(thread)。更准确的定义是:线程是“一个进程内部的控制序列。在linux中,由于线程和进程都具有id,都需要调度等等相似性,因此都可以用PCB来描述和控制,线程含有PCB&am…...

为ppt中的文字配色
文字的颜色来源于ppt不可删去的图像的颜色 从各类搜索网站中搜索ppt如何配色,有如下几点: 1.可以使用对比色,表示强调。 2.可以使用近似色,使得和谐统一。 3.最好一张ppt中,使用的颜色不超过三种主要颜色。 但我想强调…...
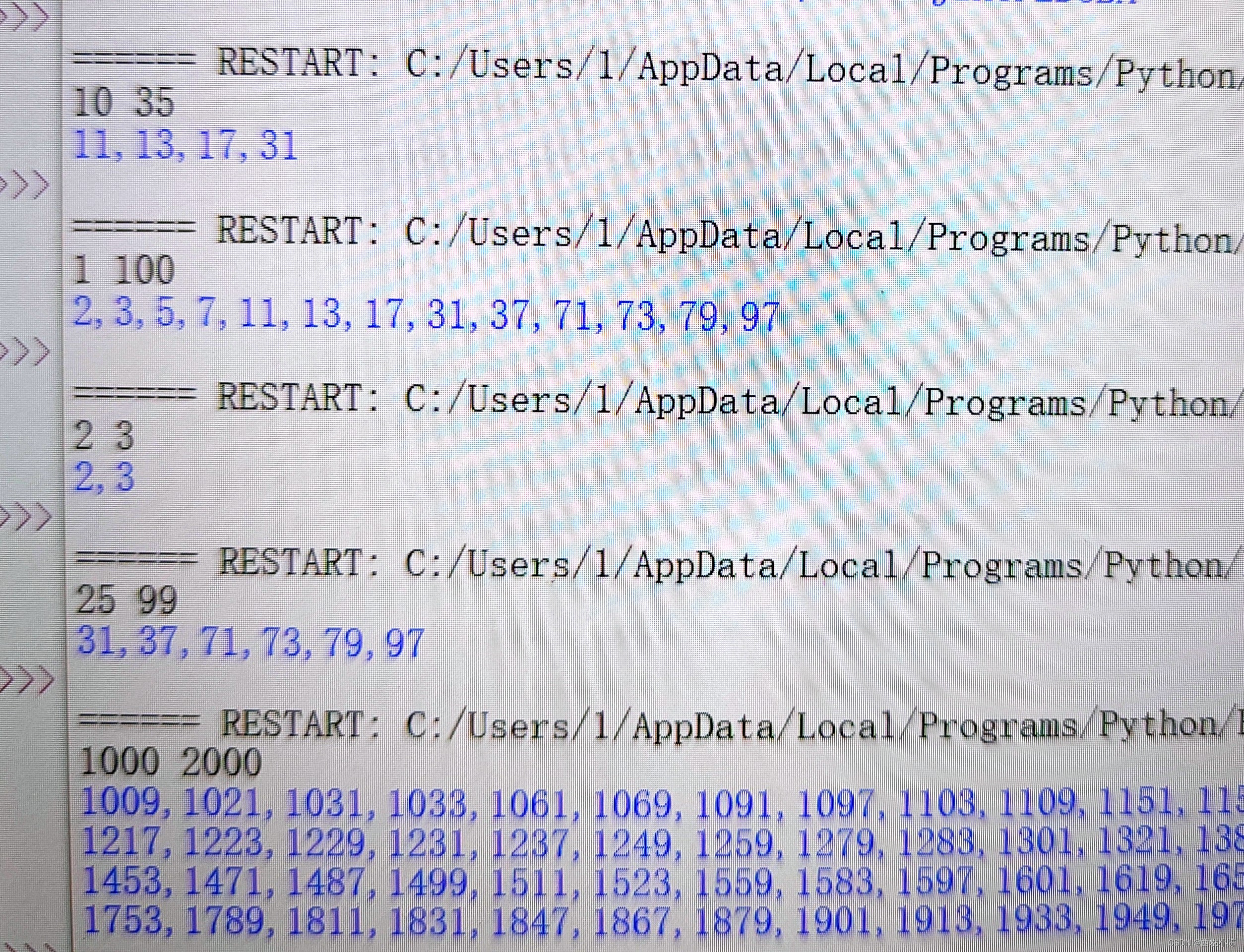
python-区间内的真素数(赛氪OJ)
[题目描述] 找出正整数 M 和 N 之间(N 不小于 M)的所有真素数。真素数的定义:如果一个正整数 P 为素数,且其反序也为素数,那么 P 就为真素数。 例如,11,13 均为真素数,因为 11 的反序…...

TCP/IP、UDP、HTTP 协议介绍比较和总结
TCP/IP、UDP、HTTP是网络通信中的三种重要协议,各自具有不同的特点和应用场景。以下是对这三种协议的详细介绍、比较和总结。 TCP/IP协议 传输控制协议/互联网协议(TCP/IP, Transmission Control Protocol/Internet Protocol) 特点: 可靠性:TCP提供可靠的通信,通过握手…...

Unity Meta Quest 开发:如何在每只手指上添加 Poke 交互
XR 开发社区: SpatialXR社区:完整课程、项目下载、项目孵化宣发、答疑、投融资、专属圈子 找到玩家物体 OVRCameraRig 下的子物体 HandInteractorsRight/Left(分别管理左右手的 Interactor)下的 HandPokeInteractor 子物体&#x…...

MyBatis的原理?
MyBatis是一个优秀的持久层框架,它支持定制化SQL、存储过程以及高级映射。MyBatis避免了几乎所有的JDBC代码和手动设置参数及获取结果集。MyBatis可以通过简单的XML或注解来配置和映射原生类型、接口和Java的POJOs(Plain Old Java Objects)为…...

数学基础【俗说矩阵】:齐次线性方程和非齐次线性方程求解-学习笔记
一、矩阵基础知识 二元一次方程的传统解法 不论是代入消元法还是加减消元法都统称 【高斯消元法】。 齐次方程组和非齐次方程组 线性方程组的解 线性方程的向量展示 向量规则 矩阵的高斯消元和初等行变行及其规则 高斯消元规则 初等行变换 矩阵经初等行变换成阶梯矩阵&…...

乐尚代驾项目概述
前言 2024年7月17日,最近终于在低效率的情况下把java及其生态的知识点背的差不多了,投了两个礼拜的简历,就一个面试,总结了几点原因。 市场环境不好 要知道,前两年找工作,都不需要投简历,把简历…...

脱发的 7 个原因,不能再瞒着大家了!
《黄帝内经》记载,“发为血之余,肾其华在发”。乌发飘逸的秀发,是年轻之体气血充盈、生机勃发的象征,更是纯粹天然、淡泊雅致的东方美学的体现。年轻一代不仅关注身体的养生,对头发的保护与保养也有了新的认识。头发已经成为当代年…...

Vim使用教程
目录 引言1. Vim的基本概念1.1 模式1.2 启动和退出 2. 基础操作2.1 导航2.2 插入文本2.3 删除和复制2.4 查找和替换 3. 高级功能3.1 多文件编辑3.2 宏录制和执行3.3 使用插件3.4 自定义快捷键 4. Vim脚本和自定义配置4.1 基本配置4.2 编写Vim脚本 5. 实用技巧5.1 快速移动5.2 批…...
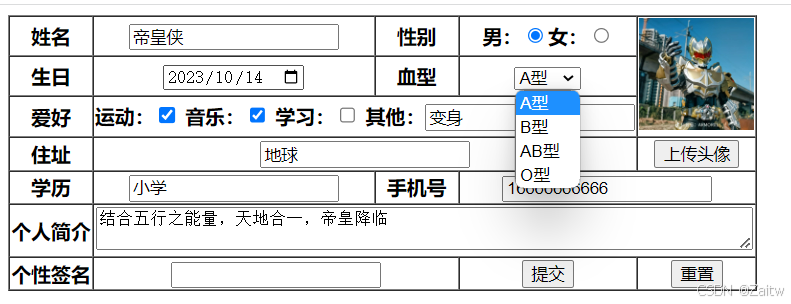
前端开发体系+html文件详解
目录 html骨架 body主体内基本元素 基本元素 超文本(超链接跳转) 锚点 图片标签 列表标签 表格标签 框架标签(窗口标签) 音频标签 视频标签 VScode编译器 输入框 字体样式 实例展示: 首先简要介绍前端的整…...

小程序中用于跳转页面的5个api是什么和区别
在微信小程序中,用于页面跳转的API主要有以下几个,但通常不需要5个那么多,因为它们的功能各有侧重,用于不同的跳转场景。以下是这些API及其详细代码和区别: wx.navigateTo(OBJECT) 用于保留当前页面,跳转到…...

翁恺-C语言程序设计-10-0. 说反话
10-0. 说反话 给定一句英语,要求你编写程序,将句中所有单词的顺序颠倒输出。 输入格式:测试输入包含一个测试用例,在一行内给出总长度不超过80的字符串。字符串由若干单词和若干空格组成,其中单词是由英文字母&#…...
- 如何跟大模型对话)
langchain 入门指南(二)- 如何跟大模型对话
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 本文中,我们会通过一个简单的例子来展示如何使用 langchain 来调用大模型的 chat API(使用 Chat Modelÿ…...

[集成学习]基于python的Stacking分类模型的客户购买意愿分类预测
1 导入必要的库 import pandas as pd import numpy as np import missingno as msno import matplotlib.pyplot as plt from matplotlib import rcParams import seaborn as sns from sklearn.metrics import roc_curve, auc from sklearn.linear_model import LogisticRegres…...

FastApi地理坐标数据存取实践
说明: 应用Pydantic Model 验证/出入 数据, SqlAlchemy Model数据实体,Fastapi提供API机制支持。数据表的坐标字段采用Mysql的GEOMETRY类型目前还没成功使用Pydantic的Coordinate类型,待后续改良 要点: 输出的结果是…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...
