数学基础【俗说矩阵】:齐次线性方程和非齐次线性方程求解-学习笔记
一、矩阵基础知识
二元一次方程的传统解法
 不论是代入消元法还是加减消元法都统称 【高斯消元法】。
不论是代入消元法还是加减消元法都统称 【高斯消元法】。
齐次方程组和非齐次方程组

线性方程组的解

线性方程的向量展示

向量规则

矩阵的高斯消元和初等行变行及其规则
高斯消元规则

初等行变换
矩阵经初等行变换成阶梯矩阵,相当于有目标地对方程组进行高斯消元,把方程组转换为容易求解的形式。
 初等行变换的步骤:
初等行变换的步骤:

初等行变换和高斯消元的规则和对应关系

二、用矩阵求齐次线性方程和非齐次线性方程
齐次线性方程的解总结
在齐次线性方程中,如果非零行行数和求解未知数个数相等,则方程组只有零解;

在齐次线性方程中,如果非零行行数个数小于求解未知数个数,则方程组存在非零解。
当存在非零解时候,找出主变量和自由变量,然后对自由变量正交赋值,自底向上地求出主变量的值,最终求出基础解系。
1、下图中主变量为x1和x2。自由变量为x3和x4。
 2、通过给x3和x4进行正交x3=1和x4=0赋值得到基础解系中的第一个向量:
2、通过给x3和x4进行正交x3=1和x4=0赋值得到基础解系中的第一个向量:
 3、通过给x3和x4进行反交x3=0和x4=1赋值得到基础解系中的第二个向量:
3、通过给x3和x4进行反交x3=0和x4=1赋值得到基础解系中的第二个向量:

4、通过给两个基础解系进行都乘以一个任意的常数k1、k2则得到齐次方程组的通解。

齐次线性方程通解过程总结

非齐次线性方程的解总结
系数矩阵和增广矩阵

在非其次线性方程中,如果阶梯系数矩阵中非零行行数、阶梯增广矩阵中非零行行数、求解未知数个数三者相等,则方程组只有唯一解;

在非其次线性方程中,如果系数矩阵中非零行行数、增广矩阵中非零行行数两者相等但小于求解未知数个数,则方程组有无穷解;

在非其次线性方程中,如果系数矩阵中非零行行数与增广矩阵中非零行行数两者不相等,则方程组无解;

非齐次线性方程通解
具有无穷解的非齐次线性方程组的通解结果
1、把x3提取后并替换成常数K后的展示

2、非齐次线性方程组通解=齐次方程组通解+非齐次方程组的特解
 3、特解向量的求法
3、特解向量的求法
在阶梯增广矩阵对应的方程组中,令全体自由变量为0,就能求出特解。

非齐次线性方程总结步骤和通解步骤
1、先判断非齐次线性方程组解的情况。

2、如果是无穷解,先找到主变量和自由变量,求出对应齐次方程组的基础解系也就是通解x’,然后再求出非齐次方程组的解系也就是特解n’,然后通解x’和特解n’的和就是非齐次线性方程的通解。
①、齐次方程组的解系方法就是把所有结果向量都赋值为0,然后对自由变量正交和反交赋值,得到齐次方程组的通解x’。

②、非齐次方程组的解析方法就是令全体自由变量为0,自底向上求出非齐次线性方程组的特解n’。

③、将齐次方程组的通解和非齐次方程组的特解相加,就是非齐次方程组的通解。

原学习视频合集链接《俗说矩阵》
相关文章:

数学基础【俗说矩阵】:齐次线性方程和非齐次线性方程求解-学习笔记
一、矩阵基础知识 二元一次方程的传统解法 不论是代入消元法还是加减消元法都统称 【高斯消元法】。 齐次方程组和非齐次方程组 线性方程组的解 线性方程的向量展示 向量规则 矩阵的高斯消元和初等行变行及其规则 高斯消元规则 初等行变换 矩阵经初等行变换成阶梯矩阵&…...

乐尚代驾项目概述
前言 2024年7月17日,最近终于在低效率的情况下把java及其生态的知识点背的差不多了,投了两个礼拜的简历,就一个面试,总结了几点原因。 市场环境不好 要知道,前两年找工作,都不需要投简历,把简历…...

脱发的 7 个原因,不能再瞒着大家了!
《黄帝内经》记载,“发为血之余,肾其华在发”。乌发飘逸的秀发,是年轻之体气血充盈、生机勃发的象征,更是纯粹天然、淡泊雅致的东方美学的体现。年轻一代不仅关注身体的养生,对头发的保护与保养也有了新的认识。头发已经成为当代年…...

Vim使用教程
目录 引言1. Vim的基本概念1.1 模式1.2 启动和退出 2. 基础操作2.1 导航2.2 插入文本2.3 删除和复制2.4 查找和替换 3. 高级功能3.1 多文件编辑3.2 宏录制和执行3.3 使用插件3.4 自定义快捷键 4. Vim脚本和自定义配置4.1 基本配置4.2 编写Vim脚本 5. 实用技巧5.1 快速移动5.2 批…...
前端开发体系+html文件详解
目录 html骨架 body主体内基本元素 基本元素 超文本(超链接跳转) 锚点 图片标签 列表标签 表格标签 框架标签(窗口标签) 音频标签 视频标签 VScode编译器 输入框 字体样式 实例展示: 首先简要介绍前端的整…...

小程序中用于跳转页面的5个api是什么和区别
在微信小程序中,用于页面跳转的API主要有以下几个,但通常不需要5个那么多,因为它们的功能各有侧重,用于不同的跳转场景。以下是这些API及其详细代码和区别: wx.navigateTo(OBJECT) 用于保留当前页面,跳转到…...

翁恺-C语言程序设计-10-0. 说反话
10-0. 说反话 给定一句英语,要求你编写程序,将句中所有单词的顺序颠倒输出。 输入格式:测试输入包含一个测试用例,在一行内给出总长度不超过80的字符串。字符串由若干单词和若干空格组成,其中单词是由英文字母&#…...
- 如何跟大模型对话)
langchain 入门指南(二)- 如何跟大模型对话
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 本文中,我们会通过一个简单的例子来展示如何使用 langchain 来调用大模型的 chat API(使用 Chat Modelÿ…...

[集成学习]基于python的Stacking分类模型的客户购买意愿分类预测
1 导入必要的库 import pandas as pd import numpy as np import missingno as msno import matplotlib.pyplot as plt from matplotlib import rcParams import seaborn as sns from sklearn.metrics import roc_curve, auc from sklearn.linear_model import LogisticRegres…...

FastApi地理坐标数据存取实践
说明: 应用Pydantic Model 验证/出入 数据, SqlAlchemy Model数据实体,Fastapi提供API机制支持。数据表的坐标字段采用Mysql的GEOMETRY类型目前还没成功使用Pydantic的Coordinate类型,待后续改良 要点: 输出的结果是…...

Docker容器——初识Docker,安装以及了解操作命令
一、Docker是什么? 是一个开源的应用容器引擎,基于go语言开发并遵循了apache2.0协议开源,用来管理容器和镜像的工具是在Linux容器里驱动运行应用的开源工具是一种轻量级的“虚拟机” 基于linux内核运行Docker的容器技术可以在一台主机上轻松为任何应用…...

JavaSE从零开始到精通
1.前置知识 JVM:java virtrual machine, java虚拟机, 专门用于执行java代码的一款软件。可以将class文件,转换为机器认识的机器码,因为我们的计算机只认识010101的二进制语言。JRE:java runtime enviroment, java运行时环境, jav…...

求解答word图标变白
把WPS卸载了之后就变成白色了,然后在注册表中把word的地址改成office word的地址之后图标变成这样了,怎么办...
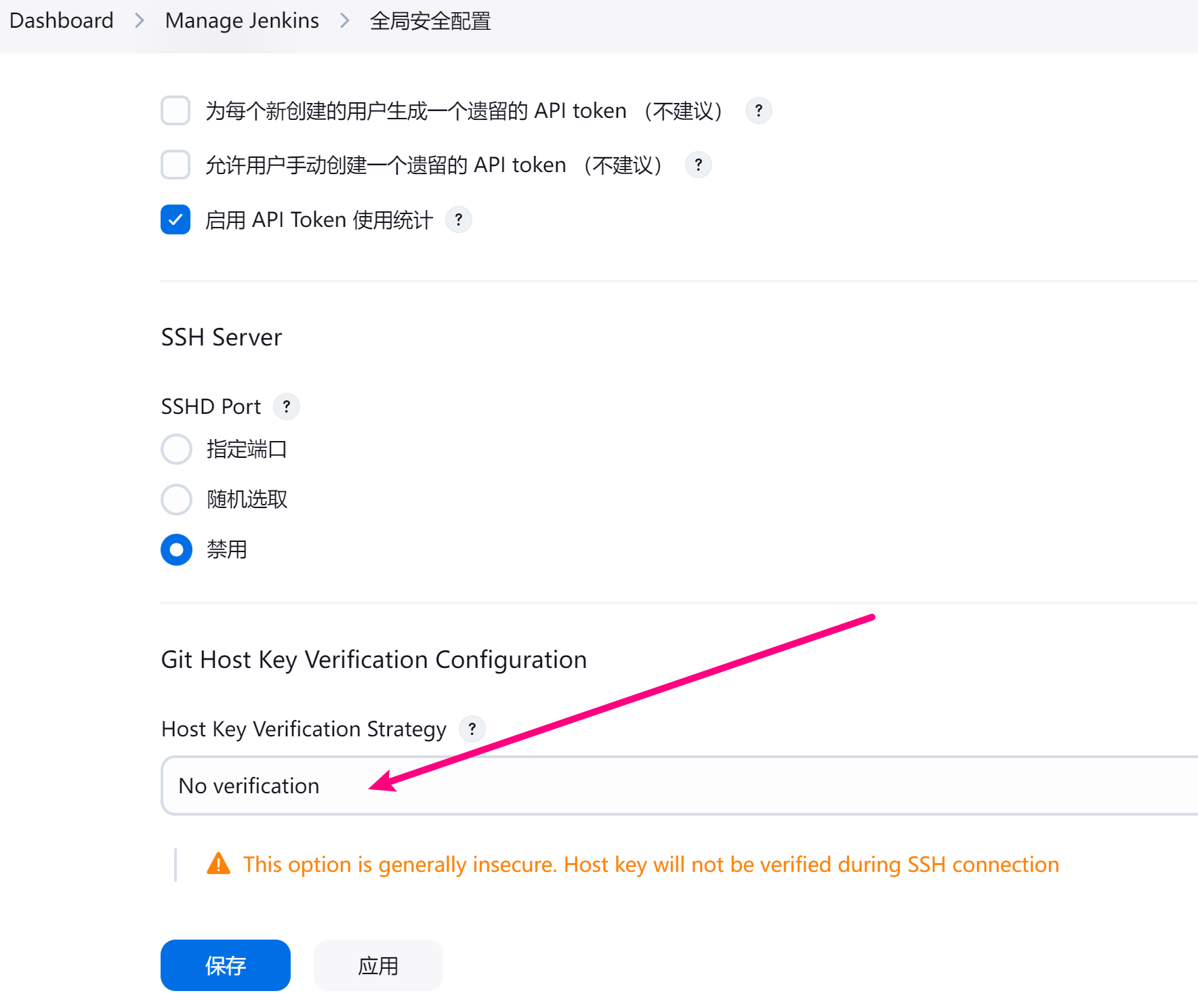
Jenkins 离线升级
1. 环境说明 环境 A: jenkins 版本:2.253使用 systemctl 管理的 jenkins 服务 环境 B: 可以上网的机器,装有 docker-compose docker 和 docker-compose 安装,这里都略了。 2. 安装旧版本 2.1 环境 A jenkins 目录打包文件 …...

Unty 崩溃问题(Burst 1.8.2)
错误代码: Assertion failed on expression: exception SCRIPTING_NULL UnityEngine.StackTraceUtility:ExtractStackTrace () Unity.Burst.BurstCompiler:SendRawCommandToCompiler (string Unity版本:2021.3.17F1,Burst 1.8.2 表现&…...

【大型实战】企业网络实验(华为核心交换、ESXI7.0vmware虚拟机、DHCP中继、服务端网络及用户端网络配置)
需求 实验 vmware网络配置(企业内部一般为ESXI) 这样服务器虚拟机使用192.168.200.X网段才能与用户侧互通 vmware虚拟机配置(DHCP服务器网络配置) 打开网络管理页面 nmtui重置一下网络连接(重启网卡) …...

vue2路由跳转是异步的
在 Vue 2 中,如果你在路由跳转函数中通过路由路径判断路径时,发现路径还是上一个路径,这是因为路由跳转是异步的。为了确保在路由跳转完成后进行判断,你可以使用路由的导航守卫或者 nextTick 来确保获取到最新的路由路径。 使用 …...

第一阶段面试题总结
1. 线程和进程的概念,区别、以及什么时候用线程什么时候用进程 1.1 线程概念 线程是进程中的一个执行单元,一个进程可以包含多个线程 线程是一个轻量级的进程 线程是CPU任务调度的最小单元 1.2 进程概念 进程是一个程序的运行实例,它包含了…...
)
设计模式(工厂模式,模板方法模式,单例模式)
单例模式: 确保一个类只有一个实例,并提供全局访问点。 单例模式举例: 配置信息类:用于存储应用程序的全局配置信息,例如数据库连接信息、日志配置等。 日志类:用于记录应用程序运行时的日志信息&#x…...
)
ES6 对象的新增方法(十四)
1. Object.assign(target, …sources) 特性:将一个或多个源对象的所有可枚举属性复制到目标对象。 用法:用于对象属性的合并。 const obj1 { a: 1, b: 2 }; const obj2 { b: 3, c: 4 }; Object.assign(obj1, obj2);console.log(obj1); // 输出&#…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

2025-05-08-deepseek本地化部署
title: 2025-05-08-deepseek 本地化部署 tags: 深度学习 程序开发 2025-05-08-deepseek 本地化部署 参考博客 本地部署 DeepSeek:小白也能轻松搞定! 如何给本地部署的 DeepSeek 投喂数据,让他更懂你 [实验目的]:理解系统架构与原…...
