【Leetcode】二十一、前缀树 + 词典中最长的单词
文章目录
- 1、背景
- 2、前缀树Trie
- 3、leetcode208:实现Trie
- 4、leetcode720:词典中最长的单词
1、背景

如上,以浏览器搜索时的自动匹配为例:

如果把所有搜索关键字放一个数组里,则:插入、搜索一个词条时,时间复杂度为O(n),判断某个前缀是否存在,时间复杂度为O(n × m),m为词条长度,因为在遍历数组时,要挨个对比数组每个元素的每个字符和词条前缀的每个字符是否相同,得两层for循环,时间复杂度太高,比如在以下数组判断是否有前缀为haha的关键字:
[goog,googl,google,bai,baidu,gi]
2、前缀树Trie
前缀树,又叫字典树,是一种数据结构,Trie,发音类似 “try”。比如存以下这些数据到前缀树:
goog,googl,google,bai,baidu,gi
效果:

root节点,一般不存数据,其下有孩子节点。以goog为例,存到第二个g时,这个单词没了,此时,这儿所在的节点,会有一个结束的Flag,以及该Flag处对应的值。从以上的分析,大致可以看出,前缀树Trie这种结构,其对象应该有以下属性:
- 孩子节点children
- 某个单词的结束标志isEnd
关于时间复杂度,如果输入字符串str,其长度为k:
- 插入:O(k)
- 搜索:O(k)
- 判断是否存在str这个前缀的词语:O(k)
关于前缀树这种结构的应用场景:
- 前缀匹配
- 词频统计(做统计,当然也可用HashMap实现)
3、leetcode208:实现Trie
以英语单词为例,26个字母,根据ASCII码转为数字,就是数组的下标。Trie类应该有个isEnd属性,因为要区分:
- 是否有str这个单词
- 是否有以str开头(为前缀)的单词
比较到str的最后一个字母,isEnd为true,说明有str这个单词,是否有这个前缀,则不用考虑isEnd。
此外,正常来说,每个Trie节点的值val也要存一下,但对英文字母不用,因为其对应的SSCII码,可以当下标,下标转一下就是字母值。

参照以上示意图,每个节点上存着一个字母(索引与ASCII码),写前缀树的实现:
public class Trie {private Trie[] children;private boolean isEnd;public Trie() {// 26个英文字母,每个节点最多26个儿子节点children = new Trie[26];isEnd = false;}public void insert(String word) {// 调用insert方法的对象,可认为是根节点Trie node = this;for (int i = 0; i < word.length(); i++) {char ch = word.charAt(i);// 字母转ASCII码,a对应97,减去a,可让值从0开始,而不是97,方便对应数组下标int index = ch - 'a';if (node.children[index] == null) {// 这是个新字母,创建一个新的节点,作为子节点// 这个节点对应的字母的值不用存,下标+97转回去就是这个节点的值node.children[index] = new Trie();}// 该判断word里的下一个字母了,node节点不再是根节点,而是第一个字母的对应的节点node = node.children[index];}// 整个word都遍历完了,结束标志为置为truenode.isEnd = true;}public boolean search(String word) {Trie node = this;for (int i = 0; i < word.length(); i++) {char ch = word.charAt(i);// 字母转ASCII码,a对应97,减去a,可让值从0开始,而不是97,方便对应数组下标int index = ch - 'a'; if (node.children[index] == null) {// 往下顺,如果有字母不一样,说明一定不存在这个单词return false;}// 检查下一个字母,替换下Tire节点node = node.children[index];}// 和判断前缀是否存在不一样,搜索,找到末尾后,末尾这儿必须有单词的结束标志isEndreturn node.isEnd;}public boolean startsWith(String prefix) {Trie node = this;for (int i = 0; i < prefix.length(); i++) {char ch = prefix.charAt(i);// 字母转ASCII码,a对应97,减去a,可让值从0开始,而不是97,方便对应数组下标int index = ch - 'a';if (node.children[index] == null) {return false;}// 检查下一个字母,替换下Tire节点node = node.children[index];}return true;}
}
搜索和判断前缀的代码重复度太高,优化下,抽取公共代码
public class Trie {private Trie[] children;private boolean isEnd;public Trie() {// 26个英文字母,每个节点最多26个儿子节点children = new Trie[26];isEnd = false;}public void insert(String word) {// 调用insert方法的对象,可认为是根节点Trie node = this;for (int i = 0; i < word.length(); i++) {char ch = word.charAt(i);// 字母转ASCII码,a对应97,减去a,可让值从0开始,而不是97,方便对应数组下标int index = ch - 'a';if (node.children[index] == null) {// 这是个新字母,创建一个新的节点,作为子节点// 这个节点对应的字母的值不用存,下标+97转回去就是这个节点的值node.children[index] = new Trie();}// 该判断word里的下一个字母了,node节点不再是根节点,而是第一个字母的对应的节点node = node.children[index];}// 整个word都遍历完了,结束标志为置为truenode.isEnd = true;}/*** 搜索和判断前缀是否存在,两个操作的公共逻辑抽取** @param str 输入的字符串* @return 返回最后一个字母对应的Trie节点,无则返回null*/public Trie getTrieNode(String str) {if (str == null) {return null;}// 调用insert方法的对象,可认为是根节点Trie node = this;for (int i = 0; i < str.length(); i++) {char ch = str.charAt(i);// 字母转ASCII码,a对应97,减去a,可让值从0开始,而不是97,方便对应数组下标int index = ch - 'a';if (node.children[index] == null) {// 往下顺,如果有字母不一样,说明一定不存在这个单词或前缀return null;}// 检查str的下一个字母,替换下Tire节点node = node.children[index];}return node;}public boolean search(String word) {Trie trieNode = getTrieNode(word);// 和判断前缀是否存在不一样,搜索,找到末尾后,末尾这儿必须有单词的结束标志isEndreturn trieNode != null && trieNode.isEnd;}public boolean startsWith(String prefix) {return getTrieNode(prefix) != null;}
}
从优化后的代码可以看到,搜索和判断前缀的区别是,判断到输入字符的最后一个字母后,搜索要有isEnd标志为true,表示有这样的单词,以免出现,搜abc,但只有abcd时也返回true的情况。而判断前缀是否存在,则不用考虑这个标志位。
4、leetcode720:词典中最长的单词

如题中示例1,能返回world,需要前面有w ⇒ wo ⇒ wor ⇒ worl这四个词语才行

将题中数组的每个单词存入前缀树,然后遍历数组。比如app单词,a字母找到了,且isEnd为true,往下ap,也找到了,且isEnd为true,如此app这个单词就是目前符合要求的。
public class P720 {public String longestWord(String[] words) {if (null == words || words.length == 0) {return "";}Trie trie = new Trie();for (String word : words) {trie.insert(word);}String result = "";// 控制精确跳到外层循环,而不是内层outerLoop:for (String word : words) {String temp = "";for (String s : word.split("")) {temp = temp + s;if (!trie.search(temp)) {// 如果有一个字母找不到,则直接看题中数组里的下一个单词continue outerLoop;}}// 判断完一个单词符号要求后,如果长度超过了result,则替换if (word.length() > result.length()) {result = word;} else if (word.length() == result.length()) {// 如果判断完一个单词符号要求后,如果长度等于result,则对比,取字典序小的// compareToIgnoreCase() 方法与 compareTo() 方法类似,但会忽略大小写result = word.compareToIgnoreCase(result) < 0 ? word : result;}}return result;}
}以上,套用了208题的Trie类的search方法,search方法只判断搜到末尾时,isEnd是否为true,即它只关心有没有world这个词,而不关心有没有w ⇒ wo ⇒ wor ⇒ worl这四个词语(isEnd为true),再修改下search方法:
public class Trie {private Trie[] children;private boolean isEnd;//略,同上一题/*** 搜索是否有word单词,以及w ⇒ wo ⇒ wor ⇒ worl这四个单词*/public boolean searchByStep(String word) {if (word == null) {return false;}// 根节点Trie node = this;for (int i = 0; i < word.length(); i++) {char ch = word.charAt(i);int index = ch - 'a';// 没有这个字母,或者这地方结束标志为false,则返回falseif (node.children[index] == null || !node.children[index].isEnd) {return false;}// 检查str的下一个字母,替换下Tire节点node = node.children[index];}// 到最后一个字母所在的节点了return node != null && node.isEnd;}
}
用新的前缀树搜索方法(判断word是否存在的同时,还要判断w ⇒ wo ⇒ wor ⇒ worl这四个是否存在),并简化下实现代码:
public class P720 {public String longestWord(String[] words) {if (null == words || words.length == 0) {return "";}Trie trie = new Trie();for (String word : words) {trie.insert(word);}String result = "";for (String word : words) {// 不符合条件,判断下一个单词if (!trie.searchByStep(word)) {continue;}// 判断完一个单词符合要求后,如果长度超过了result,则替换// 如果判断完一个单词符号要求后,如果长度等于result,则对比,取字典序小的替换result// compareToIgnoreCase() 方法与 compareTo() 方法类似,但会忽略大小写if (word.length() > result.length() || (word.length() == result.length()) && word.compareToIgnoreCase(result) < 0) {result = word;} }return result;}
}相关文章:

【Leetcode】二十一、前缀树 + 词典中最长的单词
文章目录 1、背景2、前缀树Trie3、leetcode208:实现Trie4、leetcode720:词典中最长的单词 1、背景 如上,以浏览器搜索时的自动匹配为例: 如果把所有搜索关键字放一个数组里,则:插入、搜索一个词条时&#x…...

秋招Java后端开发冲刺——Mybatis使用总结
一、基本知识 1. 介绍 MyBatis 是 Apache 的一个开源项目,它封装了 JDBC,使开发者只需要关注 SQL 语句本身,而不需要再进行繁琐的 JDBC 编码。MyBatis 可以使用简单的 XML 或注解来配置和映射原生类型、接口和 Java POJO(Plain …...
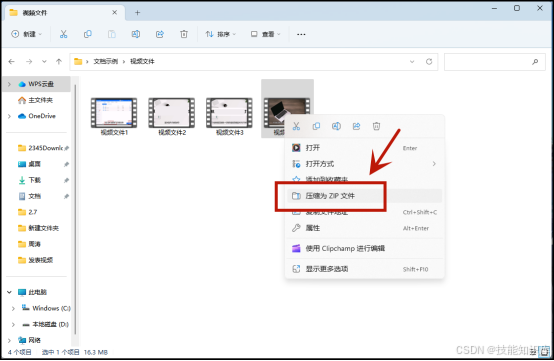
怎么压缩视频文件?简单的压缩视频方法分享
视频已成为我们日常生活中不可或缺的一部分。但随着视频质量的提高,文件大小也逐渐成为我们分享的阻碍。如何有效压缩视频文件,使其既能保持清晰,又能轻松分享?今天,给大家分享五种实用的视频压缩方法,快来…...

【Oracle】Oracle语法之递归查询
目录 递归查询使用场景备注 语法相关属性解释 案例基本使用升级版-带上递归查询的属性 总结: 递归查询 Oracle的递归查询是指在一个查询语句中使用自引用的方式进行循环迭代查询。它可以用于处理具有层次结构的数据,如组织架构、产品类别等。递归查询通…...

【教程】Vue2中使用svg矢量图
1.npm导包 npm i svg-sprite-loader --save2.创建目录放入svg文件,创建SvgIcon.js 3.SvgIcon.js const req require.context(./svg, false, /\.svg$/) const requireAll requireContext > requireContext.keys().map(requireContext) requireAll(req)4.vue.c…...

简约唯美的404HTML源码
源码介绍 简约唯美的404HTML源码,很适合做网站错误页,将下面的源码放到一个空白的html里面,然后上传到服务器里面即可使用 效果预览 完整源码 <!DOCTYPE html> <html><head><meta charset="utf-8"><title>404 Error Example<…...

PDF 转图片并插入到 EXCEL 再转PDF
pom.xml 引用 <dependency><groupId>com.aspose</groupId><artifactId>aspose-cells</artifactId><version>21.11</version></dependency><dependency><groupId>com.aspose</groupId><artifactId>as…...

jmeter之变量随机参数化以及解决多线程不会随机变化
参考链接: https://www.cnblogs.com/Testing1105/p/12743475.html jmeter 使用random函数多线程运行时数据不会随机变化?_jmeter 线程组循环执行时 变量不变-CSDN博客 1、如下图所示,需要对请求参数 autor 和phone进行随机参数化 2、目前有…...

24/7/12总结
axios Axios 是一个基于 promise 网络请求库,作用于node.js 和浏览器中。 它是 isomorphic 的(即同一套代码可以运行在浏览器和node.js中)。在服务端它使用原生 node.js http 模块, 而在客户端 (浏览端) 则使用 XMLHttpRequests。 get请求: <script>function…...

sentinel网关限流配置及使用
sentinel控制台源码:https://download.csdn.net/download/yixin605691235/89543923 sentinel控制台jar包:https://download.csdn.net/download/yixin605691235/89543931 不同环境直接修改jar包中的application.yml文件中的nacos地址就可以了。 一、网关限…...
 问题:Guideline 4.3(a) - Design - Spam)
# 如何解决 App Store 审核中的 4.3(a) 问题:Guideline 4.3(a) - Design - Spam
如何解决 App Store 审核中的 4.3(a) 问题:Guideline 4.3(a) - Design - Spam 4.3(a) 审核问题是指:你的应用与其他开发者提交的应用在二进制文件、元数据和/或概念上存在相似之处,仅有微小差别。这通常会导致你的应用被视为垃圾应用而被拒绝…...
)
最长上升子序列(LIS)
最长上升子序列(最长递增子序列,LIS) 给定长度为 n n n的序列 v v v,求此序列中严格递增(上升)的子序列长度最大值(子序列可由原序列中不连续的元素构成) 朴素DP( O ( n 2 ) O(n^2) O(n2)) 闫氏DP分析法 状态表示: 集合 d p dp dp:所有满足…...

自动驾驶车道线检测系列—3D-LaneNet: End-to-End 3D Multiple Lane Detection
文章目录 1. 摘要概述2. 背景介绍3. 方法3.1 俯视图投影3.2 网络结构3.2.1 投影变换层3.2.2 投影变换层3.2.3 道路投影预测分支 3.3 车道预测头3.4 训练和真实值关联 4. 实验4.1 合成 3D 车道数据集4.2 真实世界 3D 车道数据集4.3 评估结果4.4 评估图像仅车道检测 5. 总结和讨论…...

手工创建 postgres kamailio 数据库
测试环境如下: postgres server 16: ip 地址为 192.168.31.100,用户 postgres 的密码为 ****** kamailio v5.7.5: ip 地址为 192.168.31.101 1.1. 创建 kamailio 用户和 kamailio 数据库 ssh 登陆 kamailio (192.168.31.101)&a…...

装饰设计模式
装饰设计模式应用在IO流上面可以得到体现 装饰模式指的是在不改变原类, 不使用继承的基础上,动态地扩展一个对象的功能。 原来的inputstream已经可以读取数据了,但是是一个字节一个字节的读取的,为了优化这个我们采用了buffered,…...

Linux 线程初步解析
1.线程概念 在一个程序里的一个执行路线就叫做线程(thread)。更准确的定义是:线程是“一个进程内部的控制序列。在linux中,由于线程和进程都具有id,都需要调度等等相似性,因此都可以用PCB来描述和控制,线程含有PCB&am…...

为ppt中的文字配色
文字的颜色来源于ppt不可删去的图像的颜色 从各类搜索网站中搜索ppt如何配色,有如下几点: 1.可以使用对比色,表示强调。 2.可以使用近似色,使得和谐统一。 3.最好一张ppt中,使用的颜色不超过三种主要颜色。 但我想强调…...
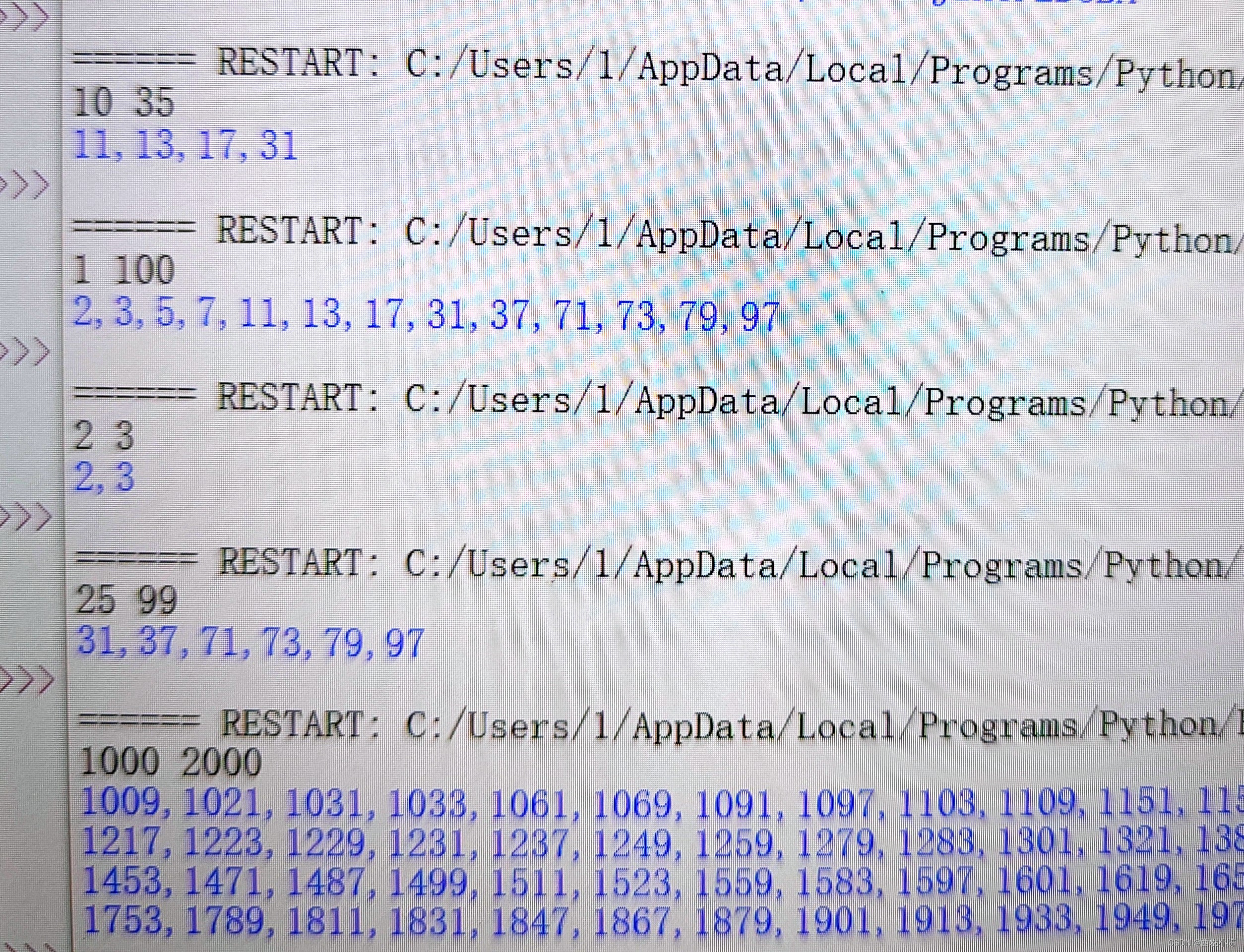
python-区间内的真素数(赛氪OJ)
[题目描述] 找出正整数 M 和 N 之间(N 不小于 M)的所有真素数。真素数的定义:如果一个正整数 P 为素数,且其反序也为素数,那么 P 就为真素数。 例如,11,13 均为真素数,因为 11 的反序…...

TCP/IP、UDP、HTTP 协议介绍比较和总结
TCP/IP、UDP、HTTP是网络通信中的三种重要协议,各自具有不同的特点和应用场景。以下是对这三种协议的详细介绍、比较和总结。 TCP/IP协议 传输控制协议/互联网协议(TCP/IP, Transmission Control Protocol/Internet Protocol) 特点: 可靠性:TCP提供可靠的通信,通过握手…...

Unity Meta Quest 开发:如何在每只手指上添加 Poke 交互
XR 开发社区: SpatialXR社区:完整课程、项目下载、项目孵化宣发、答疑、投融资、专属圈子 找到玩家物体 OVRCameraRig 下的子物体 HandInteractorsRight/Left(分别管理左右手的 Interactor)下的 HandPokeInteractor 子物体&#x…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...
