乘积量化pq：将高维向量压缩 97%

向量相似性搜索在处理大规模数据集时，往往面临着内存消耗的挑战。例如，即使是一个包含100万个密集向量的小数据集，其索引也可能需要数GB的内存。随着数据集规模的增长，尤其是高维数据，内存使用量会迅速增加，这可能导致内存管理问题。

乘积量化（PQ）是一种流行的方法，能够显著压缩高维向量，实现高达97%的内存节省，并在实际测试中将最近邻搜索的速度提高5.5倍。

更进一步，复合IVF（倒排文件索引）与PQ结合的索引方法，在不牺牲准确性的前提下，将搜索速度提高16.5倍。与非量化索引相比，整体性能提升了惊人的92倍。

本文将深入介绍PQ的各个方面，包括其工作原理、优势与局限、在Faiss中的实现方式，以及如何构建复合IVFPQ索引。还将探讨如何通过PQ实现速度和内存的优化，在处理大规模向量数据时，有效提升相似性搜索的性能。

量化是什么

量化通常是指将数据压缩到较小空间的方法。为了深入理解这一概念，需要区分量化与降维，虽然它们都旨在减少数据的存储需求，但方法和目的不同。
假设有一个高维向量，其维度为128，这些值是32位浮点数，范围在0.0到157.0之间（范围S）。通过降维，目标是产生一个更低维度的向量。

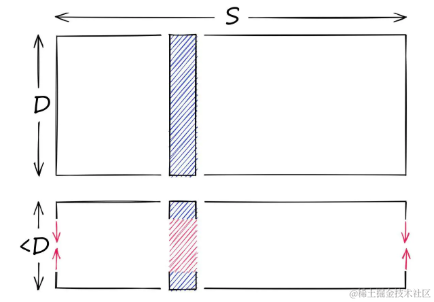
降维是降低向量的维度D，但并未改变范围S

另一方面，量化并不关心维度D，它针对潜在的值的范围，是减少S。

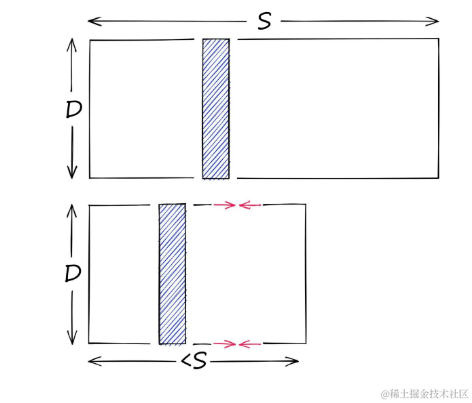
量化减少可能向量的范围S

降维：

• 降维的目标是减少高维向量的维度，例如将128维的向量转换为更低维度。
• 这一过程涉及将向量投影到更低维的空间，同时尽量保留原始数据的特征。
• 降维后，向量的数据范围（S）保持不变。

量化：

• 与降维不同，量化关注的是减少向量可能取值的范围，而不是维度。
• 量化通过将连续的数据范围映射到有限的离散值集来实现压缩。

量化可以通过多种方法实现，其中最常见的是聚类。在聚类过程中：

• 将一组向量通过聚类算法分组。
• 然后选择代表每个组的中心点，这些中心点构成了一个离散的符号集合。
• 通过上述方式，原始向量被映射到这些离散的符号上，从而显著减少可能值的范围。

量化操作将向量从具有无限可能值的连续空间转换到具有有限可能值的离散空间。这些离散值是对原始向量的符号表示。量化后的符号表示可以有多种形式，例如：

• 乘积量化（PQ） 中的聚类中心点
• 局部敏感哈希（LSH） 产生的二进制代码

这些表示方法都是将原始数据压缩的有效手段，同时保留足够的信息以进行高效的相似性搜索。

为什么使用乘积量化？

乘积量化（Product Quantization, PQ）主要用于减少索引的内存占用，这在处理大量向量时尤为重要，因为这些向量必须全部加载到内存中才能进行比较。
PQ并不是唯一的量化方法，但它在减少内存大小方面比其它方法如k-means更为有效。以下是PQ与其他方法的内存使用和量化操作复杂性的比较：

• k-means 的内存和复杂度计算公式为：$kD$
• PQ 的内存和复杂度计算公式为：$m{k}^{\ast }{D}^{\ast }=k^{1/m}D$

其中，D 代表输入向量的维度，k 表示用于表示向量的总中心点数量，m 表示将向量分割成子向量的数量。

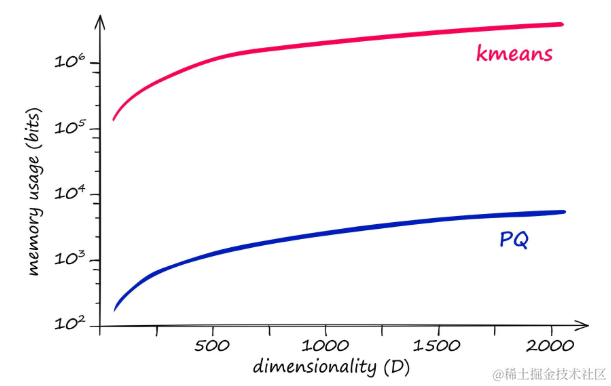
内存使用（和复杂度）与维度，使用$k=2048$和$m=8$

使用乘积量化时，需要一个较高的 k 值（例如 2048 或更高）来获得良好的结果。对于给定的向量维度 D，不使用PQ的聚类方法将导致非常高的内存需求和复杂度：

操作	内存和复杂度
k-means	$kD=2048\times 128=262144$
PQ	$mkD=(k^{1/m})\times D=(2048^{1/8})\times 128=332$

通过将向量分割成子向量，并应用到这些较小维度的子量化过程，PQ显著降低了等效内存使用和分配复杂度。

第二个重要因素是量化器的训练。量化器需要一个比 k 大几倍的数据集来进行有效的训练。没有乘积量化，这将需要大量的训练数据。

使用子量化器，只需要k/m 的倍数，尽管这可能仍然是一个相当大的数字，但与k-means相比，它可以显著减少所需的训练数据量。

乘积量化是如何工作的

乘积量化是一种高效的数据压缩技术，特别适用于大规模向量数据集。以下是PQ的基本原理和步骤：

• 向量分割： 取一个大的高维向量，将其分割成等大小的块，这些块称为子向量
• 子空间聚类： 每个子向量空间分配一个独立的聚类集，对每个子空间进行聚类以确定中心点
• 中心点分配： 将每个子向量与最近的中心点进行匹配，并用该中心点的唯一ID替换原始子向量
• 向量ID化： 原始高维向量被转换为一系列中心点的ID，这些ID构成了量化后的向量

过程结束后，需要大量内存的高维向量会减少到一个需要很少内存的小向量。假设有一个长度为 D 的向量，将其分割成m 个子向量，每个子向量的长度为 D/m。

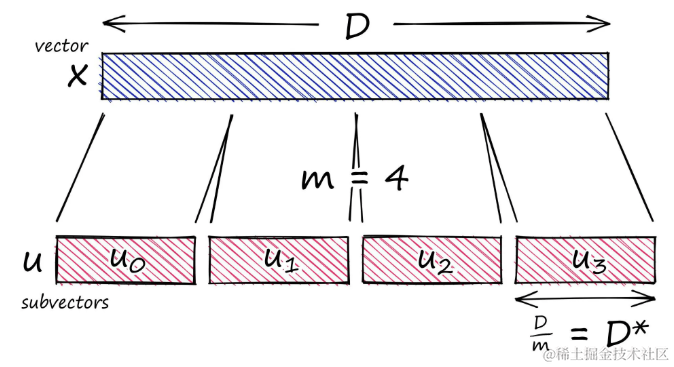
将高维向量x分割成几个子向量$u_j$

# 定义原始向量和分割参数
x = [1, 8, 3, 9, 1, 2, 9, 4, 5, 4, 6, 2]m = 4
D = len(x)assert D % m == 0D_ = int(D / m)  # 每个子向量的长度u = [x[row:row+D_] for row in range(0, D, D_)]  # 创建子向量
u# [[1, 8, 3], [9, 1, 2], [9, 4, 5], [4, 6, 2]]

在乘积量化（PQ）中，原始的高维向量首先被分解为多个子向量，每个子向量可以通过其位置 j 来引用。这个过程是实现有效量化的关键步骤。
接下来，采用聚类的方法来处理这些子向量。以一个简单的随机示例来说明，假设有一组数量庞大的向量集合，可以指定想要的聚类数量，比如说3个。然后，将通过优化这些聚类中心点来对原始向量进行分类，每个向量根据其与最近中心点的距离被分配到相应的类别中。
PQ的聚类过程与上述方法类似，但有一个关键的区别，在PQ中，不是对整个向量空间进行单一的聚类，而是每个子向量空间都拥有自己的聚类集。这意味着，实际上是在多个子空间上并行地应用聚类算法。

这种方法的优势在于：

• 并行处理：每个子空间的聚类可以独立进行，这有助于并行化计算，提高效率。
• 局部优化：每个子空间可以有自己的最优聚类中心点，这有助于捕捉局部特征。

k = 2**5
assert k % m == 0
k_ = int(k/m)
print(f"{k=}, {k_=}")
# k=32, k_=8from random import randintc = []
for j in range(m):c_j = []  # 每个j代表一个子矢量（因此也代表子量化器）位置for i in range(k_):# 每个i表示每个子空间j内的聚类/再现值位置c_ji = [randint(0, 9) for _ in range(D_)]c_j.append(c_ji)  # 将聚类质心添加到子空间列表c.append(c_j)  # 将质心的子空间列表添加到整体列表中

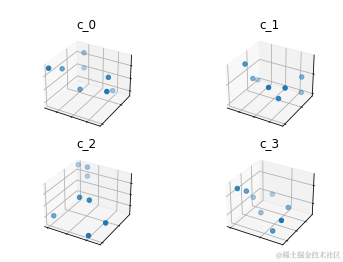
在乘积量化（PQ）中，每个子向量通过与特定的中心点匹配来实现量化。这些中心点在PQ中被称作复制值，用下标c[i]表示，其中：

• i 表示子向量在所有子向量中的索引。
• j 表示子向量在特定子空间中的位置标识符。
• 对于每个子向量空间j，存在k*个可能的中心点，每个中心点都有一个唯一的标识。

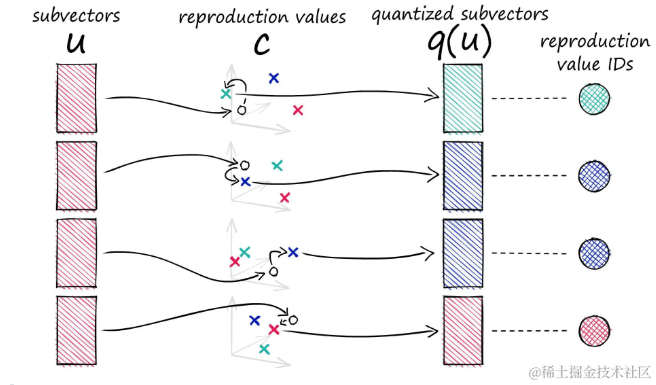
子向量被替换为特定的中心点向量，然后可以用特定于该中心点向量的唯一ID替换

def euclidean(v, u):distance = sum((x - y) ** 2 for x, y in zip(v, u)) ** .5return distancedef nearest(c_j, u_j):distance = 9e9for i in range(k_):new_dist = euclidean(c_j[i], u_j)if new_dist < distance:nearest_idx = idistance = new_distreturn nearest_idxids = []
for j in range(m):i = nearest(c[j], u[j])ids.append(i)
ids  # [1, 1, 2, 1]

当采用乘积量化（PQ）处理向量时，会经历以下步骤：

1. 向量分割：原始向量被分割为多个子向量。
2. 子向量量化：每个子向量独立地被量化，即分配给最近的集群中心点（在PQ中称为复制值）
3. 中心点ID分配：量化后，不直接存储子向量，而是用它们对应的中心点的ID来表示

在PQ中，每个中心点c[i]都有一个唯一的ID。这些ID用于后续将量化后的向量映射回原始的中心点值。这个过程不仅减少了存储需求，还便于进行快速的相似性比较。

q = []
for j in range(m):c_ji = c[j][ids[j]]  # 根据中心点ID获取中心点坐标q.extend(c_ji)  # 将中心点坐标添加到量化向量列表
q# [1, 7, 7, 6, 3, 6, 7, 4, 4, 3, 9, 6]

通过乘积量化（PQ）技术，能够显著压缩数据表示的大小，从而减少存储需求和提高处理效率。以一个简化的例子来说明，一个12维的向量被压缩成了一个4维的ID向量。虽然这里的维度较小，用于展示目的，但PQ技术的好处在更大规模的数据集上将更加明显。

考虑一个更实际的情况，从原始的128维8位整数向量转变为128维32位浮点数向量，这种转变模拟了真实世界数据的复杂性。当应用PQ技术，将这样的向量压缩到仅包含8个维度的8位整数向量时，可以看到显著的存储空间节省。

对比原始向量和量化后的向量所需的存储空间：

• 原始向量：128维 × 32位 = 4096位
• 量化向量：8维 × 8位 = 64位

这种压缩带来了64倍的存储空间减少，这是一个显著的差异。PQ技术不仅减少了存储需求，还可能提高搜索和处理速度，同时保持了数据的有用特征，为性能和压缩之间提供了良好的平衡。

PQ在Faiss中的实现

上述已经通过Python示例了解PQ的基本概念。在实际应用中，通常会采用优化过的库，如Faiss等来实现PQ。

数据获取

首先，获取数据。以Sift1M数据集为例，展示如何在Faiss中构建PQ索引，并将其与倒排文件（IVF）结合以提高搜索效率。

import shutil
import urllib.request as request
from contextlib import closing# 下载Sift1M数据集
with closing(request.urlopen('ftp://ftp.irisa.fr/local/texmex/corpus/sift.tar.gz')) as r:with open('sift.tar.gz', 'wb') as f:shutil.copyfileobj(r, f)import tarfile# 解压数据集
tar = tarfile.open('sift.tar.gz', "r:gz")
tar.extractall()import numpy as np# 读取Sift1M数据集的函数
def read_fvecs(fp):a = np.fromfile(fp, dtype='int32')d = a[0]return a.reshape(-1, d + 1)[:, 1:].copy().view('float32')# 加载数据
wb = read_fvecs('./sift/sift_base.fvecs')  # 100万个样本
xq = read_fvecs('./sift/sift_query.fvecs')  # 查询向量
xq = xq[0].reshape(1, xq.shape[1])  # 取第一个查询向量xq.shape  # (1, 128)wb.shape  # (1000000, 128)

接下来探讨如何在Faiss中构建PQ索引。

IndexPQ

在Faiss中，IndexPQ是一个实现乘积量化的索引，它用于高效地处理高维向量的近似最近邻搜索。

初始化IndexPQ

要初始化IndexPQ，需要定义三个关键参数：

• D：向量的维度
• m：将完整向量分割成子向量的数量，需要保证D能被m整除
• nbits：每个子量化器的位数，决定了每个子空间的中心点数量，$k_{=}{2}^{nbits}$

import faissD = xb.shape[1]  # 向量维度
m = 8  # 子向量数量
assert D % m == 0
nbits = 8  # 每个子量化器的位数
index = faiss.IndexPQ(D, m, nbits)  # 初始化IndexPQ

训练IndexPQ

由于PQ依赖于聚类，需要使用数据集xb来训练索引。训练过程可能需要一些时间，特别是当使用较大的nbits时。

index.is_trained  # 检查索引是否已训练index.train(xb)  # 训练索引

搜索与性能评估

接下来，使用训练好的索引进行搜索，并评估其性能。

dist, I = index.search(xq, k)  # 搜索k个最近邻 %%timeit
index.search(xq, k)# 1.49 ms ± 49.1 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

搜索操作返回最近邻的距离(dist)和索引(I)，可以将IndexPQ的召回性能与平面索引(IndexFlatL2)进行比较。

l2_index = faiss.IndexFlatL2(D)  # 初始化平面索引
l2_index.add(xb)%%time
l2_dist, l2_I = l2_index.search(xq, k)  # 平面索引搜索# CPU times: user 46.1 ms, sys: 15.1 ms, total: 61.2 ms Wall time: 15 mssum([1 for i in I[0] if i in l2_I])  # 召回率比较

上述可以得到50%的召回率，如果愿意为了PQ降低内存使用而牺牲完美结果，这是一个合理的召回率，搜索时间也减少到只有平面搜索时间的18%，可以通过使用IVF进一步改善。
PQ的低召回率是一个主要缺点，这可以通过设置更大的nbits来部分抵消，但相应的搜索时间和构建索引的耗时都会变长。对于PQ和IVFPQ索引来说，非常高的召回率是无法实现的，如果需要更高的召回率，应该考虑其他索引。

内存使用评估

最后，评估IndexPQ与平面索引在内存使用上的差异。

import osdef get_memory(index):faiss.write_index(index, './temp.index')  # 将索引写入文件file_size = os.path.getsize('./temp.index')  # 获取文件大小os.remove('./temp.index')  # 删除索引文件return file_size# 比较内存使用
get_memory(l2_index)  # 平面索引的内存使用
get_memory(index)  # IndexPQ的内存使用

IndexPQ在内存使用上表现出色，相比于平面索引，可以实现显著的内存减少98.4%。此外，通过结合倒排文件（IVF）和PQ，可以在保持较低内存占用的同时，进一步提高搜索速度。

IndexIVFPQ

为了进一步提升搜索速度，可以在PQ的基础上添加一个IVF（倒排文件）索引作为第一步，以减少搜索范围。
初始化IndexIVFPQ

初始化IVF+PQ索引需要定义几个参数：

• vecs：基础的FlatL2索引。
• nlist：Voronoi单元格的数量，必须大于等于k*（2**nbits）。
• nbits：每个子量化器的位数。
• m：子向量的数量。

vecs = faiss.IndexFlatL2(D)nlist = 2048  # Voronoi单元格数量
nbits = 8  # 子量化器的位数
m = 8  # 子向量数量
index = faiss.IndexIVFPQ(vecs, D, nlist, m, nbits)  # 初始化IVF+PQ索引
print(f"{2**nbits=}")# 2**nbits=256

新参数nlist定义了用来聚类已经量化的PQ向量的Voronoi单元格的数量。可视化一些2D的PQ向量：

2D图表显示重建的PQ向量。然而实际上永远不会使用PQ来处理2D向量，维度太低不足以将它们分割成子向量和子量化。

添加一些Voronoi单元格：

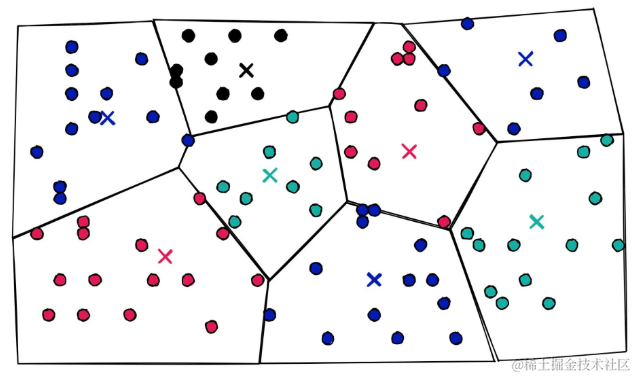
2D图表显示通过IVF分配到不同Voronoi单元格的量化PQ向量

在较高层次上，它们只是一组分区。相似的向量被分配到不同的分区（或细胞），当涉及到搜索时，将搜索限制在最近的细胞中：

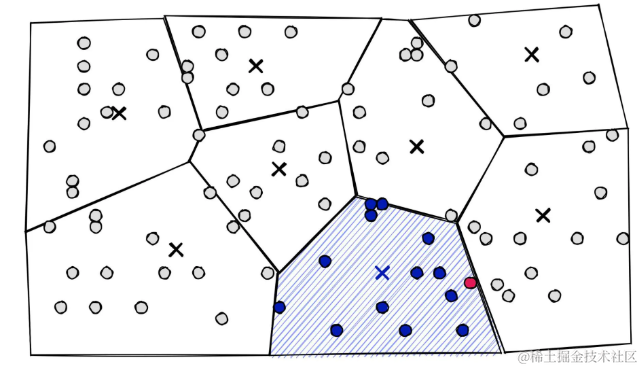
IVF允许将搜索限制在仅分配给附近细胞的向量上，粉红色点是查询向量xq

训练和搜索

训练索引并将数据添加到索引中，然后进行搜索。

index.train(xb) index.add(xb)dist, I = index.search(xq, k)  # 搜索k个最近邻%%timeit
index.search(xq, k)# 86.3 µs ± 15 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)sum([1 for i in I[0] if i in l2_I])  # 34

搜索时间非常快，只有86.3μs，但召回率从IndexPQ的50%显著下降到34%。考虑到等效参数，IndexPQ和IndexIVFPQ都应该能够达到相同的召回性能。
提高召回率的秘诀是增加nprobe参数，它控制着要在搜索范围内包括多少个最近的Voronoi细胞。

在一种极端情况下，可以通过将nprobe设置为nlist值来包括所有细胞，这将返回最大可能的召回率。但在实际应用中，需要找到实现这种召回性能的最低nprobe值。

调整召回率

通过调整nprobe参数，可以控制搜索时考虑的Voronoi单元格数量，从而影响召回率。

index.nprobe = 2048  # 搜索所有Voronoi cells
dist, I = index.search(xq, k)
sum([1 for i in I[0] if i in l2_I])  # 52index.nprobe = 2
dist, I = index.search(xq, k)
sum([1 for i in I[0] if i in l2_I])  # 39index.nprobe = 48
dist, I = index.search(xq, k)
sum([1 for i in I[0] if i in l2_I])  # 52

通过将nprobe设置为48，实现了52%的最佳召回分数，同时最小化了搜索范围（因此最大化了搜索速度）。

性能和内存使用评估

最后，评估IndexIVFPQ的性能和内存使用

# 搜索速度和召回率
%%timeit
print("Search time:", index.search(xq, k))print("Recall rate:", sum([1 for i in I[0] if i in l2_I]))# 内存使用
memory_usage = get_memory(index)
print("Memory usage:", memory_usage, "bytes")

通过添加IVF步骤，搜索时间从IndexPQ的1.49ms大幅减少到IndexIVFPQ的0.09ms，内存使用量比平面索引低96%。

通过结合IVF和PQ，IndexIVFPQ在显著减少搜索时间的同时，保持了合理的召回率和极低的内存使用。这使得IndexIVFPQ成为处理大规模数据集时的理想选择。

总结

本文深入探讨了乘积量化（Product Quantization, PQ）及其在Faiss库中的实现，特别关注了IndexPQ和IndexIVFPQ两种索引的性能对比。

乘积量化的优势

乘积量化技术通过将高维向量映射到较低维的离散空间，显著降低了内存使用量。与传统的平面索引（FlatL2）相比，IndexPQ和IndexIVFPQ在内存使用上表现出色：

• FlatL2：使用256MB内存。
• PQ：仅使用6.5MB内存，压缩率达到了97%以上。
• IVFPQ：使用9.2MB内存，略高于PQ，但仍远低于FlatL2。

搜索性能

除了内存使用，还关注了搜索速度和召回率：

• FlatL2：提供了完美的召回率（100%），但搜索速度为8.26毫秒。
• PQ：搜索速度提升至1.49毫秒，但召回率降低至50%。
• IVFPQ：结合了IVF的PQ索引在保持52%召回率的同时，将搜索速度进一步降低至0.09毫秒。

通过将倒排文件（Inverted File, IVF）技术与PQ结合，IndexIVFPQ不仅提高了搜索速度，还略微提升了召回率。这种结合利用了IVF快速缩小搜索范围的优势，同时保持了PQ的内存效率。

	FlatL2	PQ	IVFPQ
Recall (%)	100	50	52
Speed (ms)	8.26	1.49	0.09
Memory (MB)	256	6.5	9.2

测试结果表明，IndexIVFPQ在内存使用、搜索速度和召回率之间取得了良好的平衡。这项技术特别适合处理大规模数据集，能够在保持合理召回率的同时，实现快速的搜索性能和显著的内存压缩。

参考

• product-quantization
• https://youtu.be/t9mRf2S5vDI
• https://youtu.be/BMYBwbkbVec
• Product quantization for nearest neighbor search
• Jupyter Notebooks