牛客小白月赛98 (个人题解)(补全)
前言:
昨天晚上自己一个人打的小白月赛(因为准备数学期末已经写烦了),题目难度感觉越来越简单了(不在像以前一样根本写不了一点,现在看题解已经能看懂一点了),能感受到自己在不断进步,希望在暑假能更努力一点吧,,少打点游戏,多学学算法,还有web的学习也要抓起来了,这几天不是在看高数就是在打游戏,感觉好堕落。
正文:
链接:(1条未读私信) 牛客小白月赛98_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ (nowcoder.com)
A 骰子魔术:

#include<bits/stdc++.h>
using namespace std;
int a[10005];
int main(){int n,x;cin>>n>>x;for(int i=1;i<=n;i++){int d;cin>>d;a[d]++;}if(a[x])cout<<"YES";else cout<<"NO";return 0;
}桶排秒了。
B 最少剩几个?:

#include<bits/stdc++.h>
using namespace std;
int main(){int n,res=0,ans=0;cin>>n;int o=n;while(o--){int x;cin>>x;if(x%2==1)res++;}int z=n-res;if(z>=res){ans=n-2*res;}else{ans=n-2*z-((res-z)/2)*2;}cout<<ans<<endl;return 0;
}因为奇数加偶数一定是奇数,奇数乘奇数一定为奇数,分两种情况讨论,当偶数数量大于奇数的时候直接用总数减奇数数量的两倍;当奇数大于偶数的时候先减去偶数的两倍在考虑剩下的奇数即可。
C 两个函数:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=998244353;
ll quickmod(ll a, ll b, ll c)
{ll ans = 1;a = a % c;while(b){if(b&1) ans = (ans * a) % c;b = b >> 1;a = (a * a) % c;}return ans;
}
int main(){int n;cin>>n;while(n--){ll a,x,ans;cin>>a>>x;if(x==1)ans=a*x%mod;else{ans=(((a*a)%mod)*((x)*(x-1)/2%mod))%mod;}cout<<ans<<endl;}return 0;
}
我们可以将公式转化为
最后直接一边算一遍取模即可。
D 切割 01 串 2.0:

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int dp[1000][1000];
int pre[N],suf[N];
int main(){int t = 1;while(t --){int n,l,r; cin >> n >> l >> r;string s; cin >> s;s = "#" + s;// 区间dp// dp[a][b] = dp[a][k] + dp[k+1][b] + 1;for(int i = 1; i <= n ; i ++){if(s[i] == '0') pre[i] = pre[i - 1] + 1;else pre[i] = pre[i - 1];}for(int i = 1 ; i <= n ; i ++){if(s[i] == '1') suf[i] = suf[i - 1] + 1;else suf[i] = suf[i - 1];}for(int len = 2 ; len <= n ; len ++){for(int i = 1 ; i <= n - len + 1; i ++){int j = i + len - 1;for(int k = i ; k < j ; k ++){int q0 = pre[k] - pre[i - 1];int q1 = suf[j] - suf[k];int res = abs(q0 - q1);if(res >= l && res <= r)dp[i][j] = max(dp[i][j],dp[i][k] + dp[k + 1][j] + 1);}}}cout << dp[1][n];}
}比赛时这题一直想用递归,根本没去想是dp,甚至是我练过的区间dp,导致我用递归一直暴内存,怎么优化都过不了。其实细想想这题确实就是区间dp,因为从小区间推导到大区间就免去了对一次切割产生两个子段进行·递归的过程,详情可以见代码。
E and xor or:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=5e5+5;
ll a[N];
ll n,k1,k2;
ll work(int x){ll ans=0,cnt=0;for(int i=1;i<=n;i++){bool flag=true;for(int j=x;j<=60;j++){int u=a[i]>>j&1;int v=a[i-1]>>j&1;if(u!=v){flag=false;}}if(flag)cnt++;else{ans+=cnt*(cnt+1)/2;cnt=1;}}ans+=cnt*(cnt+1)/2;return ans;
}
int main(){cin>>n>>k1>>k2;for(int i=1;i<=n;i++){cin>>a[i];}cout<<work(k2)-work(k1)<<endl;return 0;
}看了题解发现这题还挺简单,
利用前缀和的思想,用所有结果小于 2^k2的子数组个数 - 所有结果小于2^k1的子数组个数,即为答案。
发现这个 2^k 刚好只有一位(二进制下),要结果小于它,则必须满足在二进制中 k ~ 60 位中不能有 1。 根据题目条件,满足不能有 1 即这个子数组元素在k ~ 60位的每一位不能同时存在 1 和 0。
F 绝妙的手法:

看了下题解的代码直接给我吓跑了,代码量还挺大的。
2024.7.12补:
出题人出来说这题出错了,所以不用补了。这又何尝不是另一种补完呢(
后记:
话说后天就考高数了我还一道题没写是不是有点不务正业了(
相关文章:

牛客小白月赛98 (个人题解)(补全)
前言: 昨天晚上自己一个人打的小白月赛(因为准备数学期末已经写烦了),题目难度感觉越来越简单了(不在像以前一样根本写不了一点,现在看题解已经能看懂一点了),能感受到自己在不断进步…...

Ubuntu压缩解压各类型文件
在Ubuntu系统中,解压不同格式的压缩文件可能需要安装不同的工具。以下是一些常见的压缩格式和相应的安装命令: ZIP文件: 工具:unzip 安装命令: sudo apt install unzip 解压命令 unzip filename.zip 如果需要保留目录…...

昇思学习打卡-20-生成式/GAN图像生成
文章目录 网络介绍生成器和判别器的博弈过程数据集可视化模型细节训练过程网络优缺点优点缺点 网络介绍 GAN通过设计生成模型和判别模型这两个模块,使其互相博弈学习产生了相当好的输出。 GAN模型的核心在于提出了通过对抗过程来估计生成模型这一全新框架。在这个…...

javafx、node js、socket、OpenGL多线程
机器学习、算法、人工智能、汇编(mips、arm、8086)、操作系统、数据挖掘、编译原理、计算机网络、Arena软件、linux xv6、racket、shell、Linux、PHP、Haskell、Scala、spark、UML、mathematica、GUI、javafx、node js、socket、OpenGL、多线程、qt、数据…...

【学习笔记】无人机(UAV)在3GPP系统中的增强支持(七)-通过无人机实现无线接入的独立部署
引言 本文是3GPP TR 22.829 V17.1.0技术报告,专注于无人机(UAV)在3GPP系统中的增强支持。文章提出了多个无人机应用场景,分析了相应的能力要求,并建议了新的服务级别要求和关键性能指标(KPIs)。…...

模糊综合评价
对多因素影响的事务的评价(如人才,方案,成果),有时难以给出影响的确切表达,此时可以采取模糊综合评价的方法。 该方法可以对人,事,物进行比较全面而又定量化的评价。 实例1ÿ…...

系统测试-白盒测试学习
目录 1、语句覆盖法: 2、判定覆盖法: 3、条件覆盖法: 4、判定条件覆盖: 5、条件组合的覆盖: 6、路径覆盖: 黑盒:需求 白盒:主要用于单元测试 1、语句覆盖法: 程序…...

UI设计工具选择指南:Sketch、XD、Figma、即时设计
在数字产品设计产业链中,UI设计师往往起着连接前后的作用。产品经理从一个“需求”开始,制定一个抽象的产品概念原型。UI设计师通过视觉呈现将抽象概念具体化,完成线框图交互逻辑视觉用户体验,最终输出高保真原型,并将…...

Pycharm 导入 conda 环境
使用时经常在此处卡壳,在此做个记录。 这个位置选择 conda 安装路径下的 python.exe 文件即可...
)
Vue封装Tooltip(提示工具)
<template> <div class"tooltip" mouseover"showTooltip" mouseleave"hideTooltip"> <slot></slot> <!-- 使用slot来接收传入的内容 --> <span class"tooltiptext" v-if"visible">{…...

Go 1.19.4 函数-Day 08
1. 函数概念和调用原理 1.1 基本介绍 函数是基本的代码块,用于执行一个任务。 Go 语言最少有个 main() 函数。 你可以通过函数来划分不同功能,逻辑上每个函数执行的是指定的任务。 函数声明告诉了编译器函数的名称,返回类型,和参…...

Docker-Nvidia(NVIDIA Container Toolkit)
安装NVIDIA Container Toolkit工具,支持docker使用GPU 目录 1.NVIDIA Container Toolkit 安装1.1 nvidia-docker安装1.2 验证1.2.1 验证安装1.2.2 额外补充 1.NVIDIA Container Toolkit 安装 1.1 nvidia-docker安装 NVIDIA/nvidia-docker Installing the NVIDIA …...

Mongodb 3.6 数据恢复操作
一、安装MongoDB 忽略 二、创建账号和授权 在新的MongoDB上创建用户管理员。先切换到admin库,然后通过命令创建数据库管理员账号和密码。最后再验证账号密码是否创建成功! use admin db.createUser({user:"root",pwd:"123456Ab",…...

C++ | Leetcode C++题解之第238题除自身以外数组的乘积
题目: 题解: class Solution { public:vector<int> productExceptSelf(vector<int>& nums) {int length nums.size();// L 和 R 分别表示左右两侧的乘积列表vector<int> L(length, 0), R(length, 0);vector<int> answer(l…...

挂耳式蓝牙耳机什么牌子好?这五款综合表现遥遥领先
为什么这几年开放式耳机受到了越来越多消费者的喜爱?我想是因为它全方位的弥补了入耳式耳机堵塞耳朵、不够安全健康的缺陷,真正做到了安全性与舒适性兼得。那么刚入坑开放式耳机的小白该如何挑选一款品质较高的开放式耳机呢?挂耳式蓝牙耳机什…...

防火墙-NAT策略和智能选路
一、背景技术 在日常网络环境,内部网络想要访问外网无法直接进行通信,这时候就需要进行NAT地址转换,而在防火墙上配置NAT和路由器上有点小区别,思路基本一致,这次主要就以防火防火墙配置NAT策略为例,防火墙…...

一键优雅为Ubuntu20.04服务器挂载新磁盘
itopen组织1、提供OpenHarmony优雅实用的小工具2、手把手适配riscv qemu linux的三方库移植3、未来计划riscv qemu ohos的三方库移植 小程序开发4、一切拥抱开源,拥抱国产化 一、小于2T磁盘挂载方式 1.1 安装磁盘到电脑后启动系统 1.2 查找未分区的磁盘 打…...
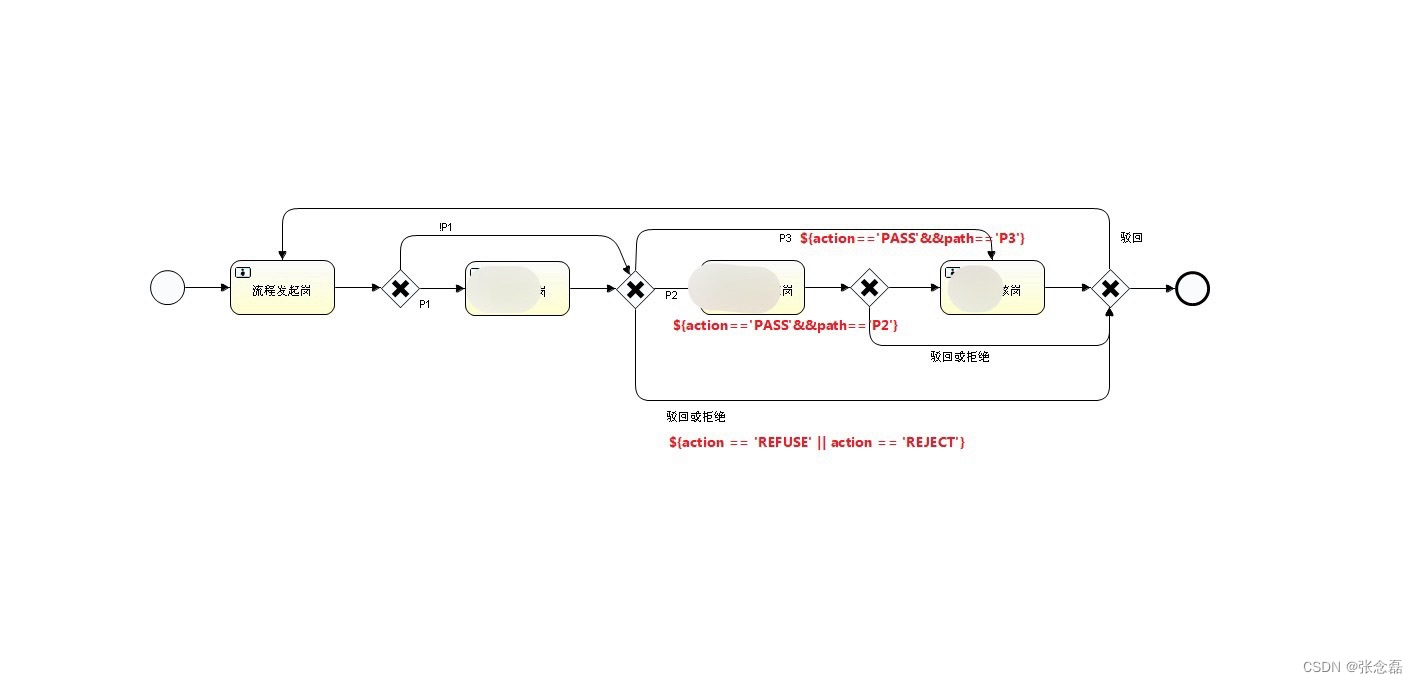
踩坑日记 | 记一次流程图问题排查
踩坑日记:记一次流程图问题排查 标签: activiti | 流程 引言 今天排查了一个流程图问题,耗时2个小时终于解决,记录下来 现象 流程审批驳回报错:Unknown property used in expression: ${xxxx} 使用的是 activiti …...
安装mysql)
数据建设实践之大数据平台(四)安装mysql
安装mysql 卸载mysql [bigdatanode101 ~]$ sudo rpm -qa | grep mariadb | xargs sudo rpm -e --nodeps 上传安装包到/opt/software目录并解压 [bigdatanode101 software]$ tar -xf mysql-5.7.28-1.el7.x86_64.rpm-bundle.tar -C mysql_lib/ 到mysql_lib目录下顺序安装 …...

MongoDB常用命令大全,概述、备份恢复
文章目录 一、MongoDB简介二、服务启动停止、连接三、数据库相关四、集合操作五、文档操作六、数据备份与恢复/导入导出数据6.1 mongodump备份数据库6.2 mongorestore还原数据库6.3 mongoexport导出表 或 表中部分字段6.4 mongoimport导入表 或 表中部分字段 七、其他常用命令八…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...
