【JavaScript 算法】贪心算法:局部最优解的构建


文章目录
- 一、贪心算法的基本概念
- 贪心算法的适用场景
- 二、经典问题及其 JavaScript 实现
- 1. 零钱兑换问题
- 2. 活动选择问题
- 3. 分配问题
- 三、贪心算法的应用
- 四、总结

贪心算法(Greedy Algorithm)是一种逐步构建解决方案的方法。在每一步选择中,贪心算法总是选择在当前看来最优的选择,希望通过这些局部最优选择最终能构建出全局最优解。贪心算法的特点是简单高效,但它并不总能保证得到最优解。
一、贪心算法的基本概念
贪心算法的核心思想是每一步都选择当前最优的决策,不考虑未来的影响。贪心算法的基本步骤通常包括以下几个:
- 选择:选择当前最优的选项。
- 验证:验证当前选择是否可行(通常包括是否满足约束条件)。
- 构建:将当前选择加入到最终的解决方案中。
贪心算法的适用场景
贪心算法通常适用于以下场景:
- 最小生成树:如Kruskal和Prim算法。
- 最短路径问题:如Dijkstra算法。
- 区间调度问题:如选择最多的不重叠区间。
二、经典问题及其 JavaScript 实现
1. 零钱兑换问题
假设我们有几种不同面值的硬币,1元、2元和5元。我们希望用最少数量的硬币来凑出某个金额。
问题描述:给定不同面值的硬币和一个总金额,求最少数量的硬币。
/*** 求最少数量的硬币组合* @param {number[]} coins - 硬币面值数组* @param {number} amount - 总金额* @returns {number} - 最少硬币数量,如果无法凑出总金额返回 -1*/
function coinChange(coins, amount) {// 硬币面值从大到小排序coins.sort((a, b) => b - a);let count = 0;for (let coin of coins) {// 尽量使用当前面值最大的硬币let num = Math.floor(amount / coin);count += num;amount -= num * coin;// 如果总金额为 0,直接返回if (amount === 0) return count;}// 如果无法凑出总金额,返回 -1return -1;
}// 示例:用1元、2元和5元凑出11元的最少硬币数量
console.log(coinChange([1, 2, 5], 11)); // 输出 3 (5 + 5 + 1)
2. 活动选择问题
假设我们有一组活动,每个活动有开始时间和结束时间。我们希望选择尽可能多的活动,使得它们互不重叠。
问题描述:给定一组活动,选择尽可能多的不重叠活动。
/*** 求最多的不重叠活动数量* @param {number[][]} activities - 活动的开始和结束时间数组* @returns {number} - 最多不重叠活动数量*/
function maxActivities(activities) {// 按照活动结束时间排序activities.sort((a, b) => a[1] - b[1]);let count = 0;let end = 0;for (let activity of activities) {if (activity[0] >= end) {// 选择当前活动count++;end = activity[1];}}return count;
}// 示例:选择最多的不重叠活动
console.log(maxActivities([[1, 3], [2, 4], [3, 5], [0, 6], [5, 7], [8, 9], [5, 9]]));
// 输出 4 (选择活动 [1, 3], [3, 5], [5, 7], [8, 9])
3. 分配问题
假设我们有一组任务和一组工人,每个工人能完成的任务数量有限。我们希望尽可能多地完成任务。
问题描述:给定任务和工人的能力,尽可能多地分配任务。
/*** 求最多分配任务数量* @param {number[]} tasks - 任务难度数组* @param {number[]} workers - 工人能力数组* @returns {number} - 最多分配任务数量*/
function maxTaskAssignment(tasks, workers) {// 任务和工人分别排序tasks.sort((a, b) => a - b);workers.sort((a, b) => a - b);let taskIndex = 0;let workerIndex = 0;let count = 0;while (taskIndex < tasks.length && workerIndex < workers.length) {if (workers[workerIndex] >= tasks[taskIndex]) {// 分配任务给当前工人count++;taskIndex++;}workerIndex++;}return count;
}// 示例:尽可能多地分配任务
console.log(maxTaskAssignment([1, 2, 3], [3, 2, 1])); // 输出 3 (每个工人完成一个任务)
三、贪心算法的应用
贪心算法在实际开发中有广泛的应用,常见的应用场景包括:
- 图算法:最小生成树、最短路径问题。
- 活动选择:选择最多的不重叠活动。
- 任务分配:将任务尽可能多地分配给工人。
- 区间覆盖:用最少数量的区间覆盖所有点。
四、总结
贪心算法是一种通过局部最优选择构建全局最优解的方法。虽然它不总能保证得到最优解,但在许多实际问题中表现良好。通过理解和应用贪心算法,我们可以有效地解决许多复杂的优化问题。希望通过本文的介绍,大家能够更好地理解和应用贪心算法。
相关文章:

【JavaScript 算法】贪心算法:局部最优解的构建
🔥 个人主页:空白诗 文章目录 一、贪心算法的基本概念贪心算法的适用场景 二、经典问题及其 JavaScript 实现1. 零钱兑换问题2. 活动选择问题3. 分配问题 三、贪心算法的应用四、总结 贪心算法(Greedy Algorithm)是一种逐步构建解…...

Azcopy Sync同步Azure文件共享
文章目录 Azcopy Sync同步文件共享一、工作原理二、安装 AzCopy在 Windows 上在 Linux 上 三、资源准备1. 创建源和目标 Azure 存储账户2. 创建源和目标文件共享3. 确定路径4. 生成源和目的存储账户的共享访问签名(SAS)令牌配置权限示例生成的 URL 四、A…...

单例模式 饿汉式和懒汉式的区别
单例模式(Singleton Pattern)是设计模式中最简单、最常见、最容易实现的一种模式。它确保一个类仅有一个实例,并提供一个全局访问点。单例模式主要有两种实现方式:饿汉式(Eager Initialization)和懒汉式&am…...

Python中的模块和包的定义以及如何在Python中导入和使用它们
在Python中,模块(Module)和包(Package)是组织代码以便重用和共享的基本单元。它们使得Python代码更加模块化,易于管理和维护。 模块(Module) 模块是一个包含Python代码的文件&…...
)
设计模式使用场景实现示例及优缺点(结构型模式——组合模式)
结构型模式 组合模式(Composite Pattern) 组合模式使得用户对单个对象和组合对象的使用具有一致性。 有时候又叫做部分-整体模式,它使我们树型结构的问题中,模糊了简单元素和复杂元素的概念,客户程序可以像处理简单元…...

《系统架构设计师教程(第2版)》第11章-未来信息综合技术-06-云计算(Cloud Computing) 技术概述
文章目录 1. 相关概念2. 云计算的服务方式2.1 软件即服务 (SaaS)2.2 平台即服务 (PaaS)2.3 基础设施即服务 (IaaS)2.4 三种服务方式的分析2.4.1 在灵活性2.4.2 方便性方 3. 云计算的部署模式3.1 公有云3.2 社区云3.3 私有云3.4 混合云 4. 云计算的发展历程4.1 虚拟化技术4.2 分…...

网络安全工作者如何解决网络拥堵
网络如同现代社会的血管,承载着信息的血液流动。然而,随着数据流量的激增,网络拥堵已成为不容忽视的问题,它像是一场数字世界的交通堵塞,减缓了信息传递的速度,扰乱了网络空间的秩序。作为网络安全的守护者…...

电脑显示mfc140u.dll丢失的修复方法,总结7种有效的方法
mfc140u.dll是什么?为什么电脑会出现mfc140u.dll丢失?那么mfc140u.dll丢失会给电脑带来什么影响?mfc140u.dll丢失怎么办?今天详细给大家一一探讨一下mfc140u.dll文件与mfc140u.dll丢失的多种不同解决方法分享! 一、mfc…...

ospf的MGRE实验
第一步:配IP [R1-GigabitEthernet0/0/0]ip address 12.0.0.1 24 [R1-GigabitEthernet0/0/1]ip address 21.0.0.1 24 [R1-LoopBack0]ip address 192.168.1.1 24 [ISP-GigabitEthernet0/0/0]ip address 12.0.0.2 24 [ISP-GigabitEthernet0/0/1]ip address 21.0.0.2 24…...

开发指南047-前端模块版本
平台前端框架内置了一个文件version.vue <template> <div> <br> 应用名称: {{name}} <br> 当前版本:{{version}} <br> 服务网关: {{gateway}} </div> </template> <scrip…...

c#中的字符串方法
Concat() String.Concat(字符串1 字符串n) 字符串拼接 Contains () 字符串1.Contains(字符串2) 字符串1是否包含字符串2返回布尔值 CopyTo() 字符串1.CopyTo(0,空数组,0,5); 从哪开始 复制到哪里 从哪开始存 存储的个数 tartsWith 字符串1.StartsWith("字符串") 以…...

成像光谱遥感技术中的AI革命:ChatGPT
遥感技术主要通过卫星和飞机从远处观察和测量我们的环境,是理解和监测地球物理、化学和生物系统的基石。ChatGPT是由OpenAI开发的最先进的语言模型,在理解和生成人类语言方面表现出了非凡的能力,ChatGPT在遥感中的应用,人工智能在…...

学习分布式事务遇到的小bug
一、介绍Seata 在处理分布式事务时我用到是Seata,Seata的事务管理中有三个重要的角色: TC (Transaction Coordinator) - 事务协调者:维护全局和分支事务的状态,协调全局事务提交或回滚。 TM (Transaction Manager) - 事务管理器…...

ElasticSearch学习之路
前言 为什么学ElasticSearch? 数据一般有如下三种类型: 结构化数据,如:MySQL的表,一般通过索引提高查询效率非结构化数据,如:图片、音频等不能用表结构表示的数据,一般保存到mong…...
 翻转二叉树 对称二叉树 二叉树的深度)
(C++二叉树02) 翻转二叉树 对称二叉树 二叉树的深度
226、翻转二叉树 递归法: 交换两个结点可以用swap()方法 class Solution { public:TreeNode* invertTree(TreeNode* root) {if(root NULL) return NULL;TreeNode* tem root->left;root->left root->right;root->right tem;invertTree(root->l…...

高阶面试-mongodb
mongodb的特点,为什么使用他 nosql数据库,前端到后端到数据库,都是json,无模式,数据模型发生变更,不需要强制更新表结构,可以快速实现需求迭代。 天生分布式,高可用,处…...

MySQL数据库慢查询日志、SQL分析、数据库诊断
1 数据库调优维度 业务需求:勇敢地对不合理的需求说不系统架构:做架构设计的时候,应充分考虑业务的实际情况,考虑好数据库的各种选择(读写分离?高可用?实例个数?分库分表?用什么数据库?)SQL及索引:根据需求编写良…...

[短笔记] Ubuntu配置环境变量的最佳实践
结论: 不确定是否要设为系统,则先针对当前用户设,写~/.profile确定为系统级,写/etc/environment,注意无需export不推荐写在~/.bashrc(Ubuntu不推荐,理由见references) References&…...

怎样在 PostgreSQL 中优化对多表关联的连接条件选择?
🍅关注博主🎗️ 带你畅游技术世界,不错过每一次成长机会!📚领书:PostgreSQL 入门到精通.pdf 文章目录 怎样在 PostgreSQL 中优化对多表关联的连接条件选择一、理解多表关联的基本概念二、选择合适的连接条件…...
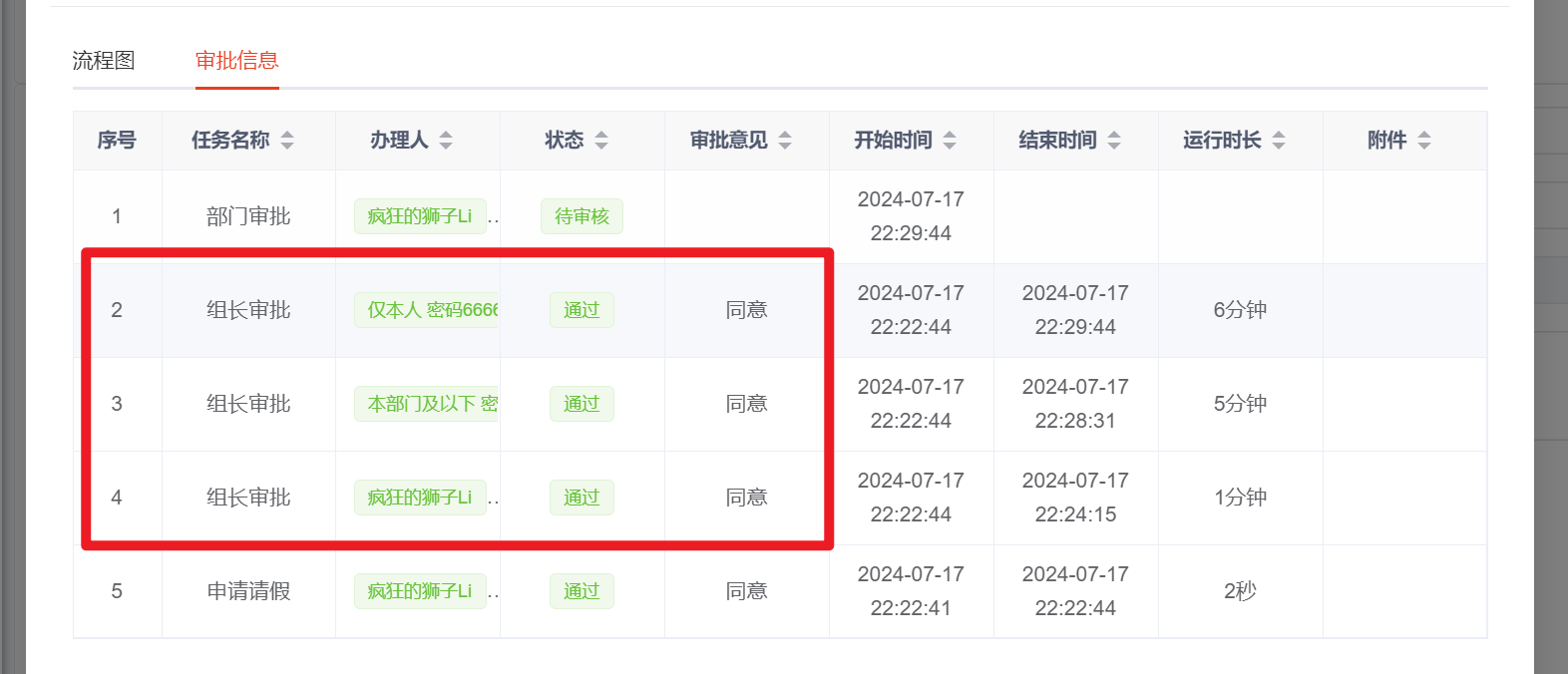
【Flowable | 第四篇】flowable工作流多任务实例节点实现会签/或签
文章目录 5.flowable工作流多任务实例节点实现会签/或签5.1会签/或签概念5.2多实例配置说明5.3会签例子5.3.1用户候选人配置5.3.2多实例配置5.3.3执行监听器配置5.3.5测试 5.flowable工作流多任务实例节点实现会签/或签 5.1会签/或签概念 我们在本篇中,将使用多任…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
