【概率论三】参数估计:点估计(矩估计、极大似然法)、区间估计
文章目录
- 一. 点估计
- 1. 矩估计法
- 2. 极大似然法
- 2.1. 似然函数
- 2.2. 极大似然估计法
- 3. 评价估计量的标准
- 3.1. 无偏性
- 3.2. 有效性
- 3.3. 一致性
- 二. 区间估计
- 1. 区间估计的概念
- 2. 正态总体参数的区间估计
参数估计讲什么
- 由样本来确定未知参数
- 参数估计分为点估计与区间估计
一. 点估计
所谓点估计是指用某个确定的值或在某个确定的点来估计总体的未知参数,所以点估计又称为定值估计。

构造估计量 ( X 1 , X 2 . . . , ) (X_1, X_2..., ) (X1,X2...,)的方法很多,下面介绍常用的矩估计法和极大似然估计法。
1. 矩估计法
原点矩概念
- 原点矩(Raw Moments)是描述随机变量分布的一种数学量,它是随机变量的幂次期望。
- 具体来说,对于一个随机变量 X,其 r 阶原点矩定义为: μ r ′ = E [ X r ] \mu_r' = E[X^r] μr′=E[Xr] 其中 E 表示期望运算符。
- 假设 X 是一个服从正态分布的随机变量,我们可以用原点矩计算其各阶矩:
- 一阶原点矩 μ 1 ′ = E [ X ] \mu_1' = E[X] μ1′=E[X] 是正态分布的均值 μ。
- 二阶原点矩 μ 2 ′ = E [ X 2 ] \mu'_2 = E[X^2] μ2′=E[X2]是正态分布的均值 μ 和方差 σ 2 σ^2 σ2 的和,即 μ 2 ′ = Var ( X ) + ( μ ) 2 \mu2' = \text{Var}(X) + (\mu)^2 μ2′=Var(X)+(μ)2。
用样本矩估计参数
样本矩在一定程度上反映了总体矩的特征,且在样本容量n增大的条件下,样本的k阶原点矩 A k = 1 / n ∑ i = 1 n X i k A_k=1/n\sum_{i=1}^{n}X_i^k Ak=1/n∑i=1nXik 依概率收敛到总体X的k阶原点矩 μ k = E ( X k ) μ_k=E(X^k) μk=E(Xk),即 A k − P > μ k A_k-^P> μ_k Ak−P>μk(n →∞), k=1,2,…。
因而自然想到用样本矩作为相应总体矩的估计量,而以样本矩的连续函数作为相应总体矩的连续函数的估计量,这种估计方法就称为矩估计法。
矩估计法的一般做法:设总体 X ∼ F ( X ; θ 1 , θ 2 , . . . ) X \sim F ( X; θ_1, θ_2,...) X∼F(X;θ1,θ2,...)其 中 θ 1 , θ 2 θ_1, θ_2 θ1,θ2 … 均未知。

- A 1 A_1 A1 代表一阶原点矩,就是平均值,当趋于无穷时, A 1 A_1 A1 收敛于 μ 1 \mu_1 μ1
xf(x;θ)是求一阶原点矩的通用公式- 得到θ与μ的关系之后,就可得θ的矩估计值 θ ^ \hat{θ} θ^。
2. 极大似然法
极大似然估计法(Maximum Likelihood Estimation)只能在已知总体分布的前提下进行。
例如,假定一个盒子里装有许多大小相同的 黑球和白球,并且假定它们的数目之比为3∶1,但不知是白球多还是黑球多,现在有放回地从盒中抽了3个球,试根据所抽3个球中黑球的数目确定是白球多还是黑球多。

2.1. 似然函数
在极大似然估计法中,最关键的问题是如何求得似然函数,有了似然函数,问题就简单了,下面分两种情形来介绍似然函数。
(1)离散型总体
p为 X n X_n Xn 变量θ的概率
(2)连续型总体
只要知道概率分布或密度函数就可以得到关于θ的似然函数。
2.2. 极大似然估计法
主要思想
转换为求似然函数的最大值。
简化为:dlnL(θ)/dθ=0
推广到k个未知参数也适用
3. 评价估计量的标准
设总体 X X X服从 [ 0 , θ ] [0,θ ] [0,θ]上的均匀分布, 如下分别使用点估计和极大似然法来估计θ
θ ^ 矩 = 2 X ˉ \hat{θ}_矩 = 2 \bar{X} θ^矩=2Xˉ,
θ ^ L m a x 1 < = i < = n { X i } \hat{θ}_L \underset{1<=i<=n}{max}{\{X_i\}} θ^L1<=i<=nmax{Xi}
这两个估计哪一个好呢?下面我们首先讨论衡量估计量好坏的标准问题。
3.1. 无偏性
若估计量 ( X 1 , X 2 , . . . , X n ) ( X_1, X_2,...,X_n ) (X1,X2,...,Xn)的数学期望等于未知参数 ,即 E ( θ ^ ) = θ E(\hat{θ})=θ E(θ^)=θ 则称 θ ^ \hat{θ} θ^为θ的无偏估计量(Non-deviationEstimator)。
估计量 θ ^ \hat{θ} θ^ 的值不一定就是θ的真值,因为它是一个随机变量,若 θ ^ \hat{θ} θ^ 是θ的无偏估计,则尽管 θ ^ \hat{θ} θ^的值随样本值的不同而变化,但平均来说它会等于θ的真值。
3.2. 有效性
对于未知参数θ ,如果有两个无偏估计量 θ ^ 1 \hat{θ}_1 θ^1 与 θ ^ 2 \hat{θ}_2 θ^2 ,即 E ( θ ^ 1 ) E(\hat{θ}_1) E(θ^1) = E ( θ ^ 2 ) E(\hat{θ}_2) E(θ^2) =θ,那么在 θ ^ 1 \hat{θ}_1 θ^1 与 θ ^ 2 \hat{θ}_2 θ^2中谁更好呢?
此时我们自然希望θ,的平均偏差 E ( θ ^ − θ ) 2 E(\hat{θ}-θ)^2 E(θ^−θ)2越小越好,即一个好的估计量应该有尽可能小的方差,这就是有效性。如下分析:
举例说明
3.3. 一致性
随着样本的增大,n随概率收敛于θ真值
二. 区间估计
1. 区间估计的概念
μ概率的问题:
我们给出μ的大致范围,使得μ有较高的概率在这个范围内,这就是区间估计问题。
置信区间、置信概率(置信度)
定义中的随机区间 ( θ 1 , θ 2 ) (θ_1,θ_2) (θ1,θ2)的大小依赖于随机抽取的样本观测值,它可能包含θ ,也可能不包含,上式的意义是指θ在 ( θ 1 , θ 2 ) (θ_1,θ_2) (θ1,θ2)区间的概率是1-a 。
例如,若取 a=0.05,那么置信概率为1-a =0.95,这时置信区间 ( θ 1 , θ 2 ) (θ_1,θ_2) (θ1,θ2)的意义是指:在100次重复抽样所得到的100个置信区间中,大约有95个区间包含参数真值θ,有5个区间不包含真值。
2. 正态总体参数的区间估计
如果未知,则用方差代替
练习题ing
当容量很大时,由中心极限定理,下式服从标准正态分布。
相关文章:

【概率论三】参数估计:点估计(矩估计、极大似然法)、区间估计
文章目录 一. 点估计1. 矩估计法2. 极大似然法2.1. 似然函数2.2. 极大似然估计法 3. 评价估计量的标准3.1. 无偏性3.2. 有效性3.3. 一致性 二. 区间估计1. 区间估计的概念2. 正态总体参数的区间估计 参数估计讲什么 由样本来确定未知参数参数估计分为点估计与区间估计 一. 点估…...

自动化产线 搭配数据采集监控平台 创新与突破
自动化产线在现在的各行各业中应用广泛,已经是现在的生产趋势,不同的自动化生产设备充斥在各行各业中,自动化的设备会产生很多的数据,这些数据如何更科学化的管理,更优质的利用,就需要数据采集监控平台来完…...

【Karapathy大神build-nanogpt】Take Away Notes
B站翻译LINK Personal Note Andrej rebuild gpt2 in pytorch. Take Away Points Before entereing serious training, he use Shakespear’s work as a small debugging datset to see if a model can overfit. Overfitging is a should thing.If we use TF32 or BF32, (by…...

MySQL学习记录 —— 이십이 MySQL服务器日志
文章目录 1、日志介绍2、一般、慢查询日志1、一般查询日志2、慢查询日志FILE格式TABLE格式 3、错误日志4、二进制日志5、日志维护 1、日志介绍 中继服务器的数据来源于集群中的主服务。每次做一些操作时,把操作保存到重做日志,这样崩溃时就可以从重做日志…...
HTTPS请求头缺少HttpOnly和Secure属性解决方案
问题描述: 建立Filter拦截器类 package com.ruoyi.framework.security.filter;import com.ruoyi.common.core.domain.model.LoginUser; import com.ruoyi.common.utils.SecurityUtils; import com.ruoyi.common.utils.StringUtils; import com.ruoyi.framework.…...

react基础样式控制
行内样式 <div style{{width:500px, height:300px,background:#ccc,margin:200px auto}}>文本</div> class类名 注意:在react中使用class类名必须使用className 在外部src下新建index.css文件写入你的样式 .fontcolor{color:red } 在用到的页面引入…...
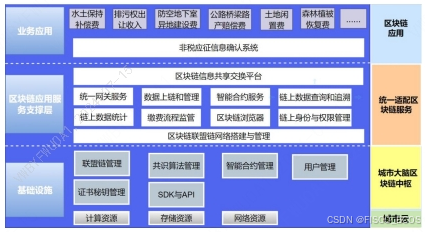
【区块链 + 智慧政务】涉税行政事业性收费“e 链通”项目 | FISCO BCOS应用案例
国内很多城市目前划转至税务部门征收的非税收入项目已达 17 项,其征管方式为行政主管部门核定后交由税务 部门征收。涉税行政事业性收费受限于传统的管理模式,缴费人、业务主管部门、税务部门、财政部门四方处于 相对孤立的状态,信息的传递靠…...

Socket、WebSocket 和 MQTT 的区别
Socket 协议 定义:操作系统提供的网络通信接口,抽象了TCP/IP协议,支持TCP和UDP。特点: 通用性:不限于Web应用,适用于各种网络通信。协议级别:直接使用TCP/UDP,需要手动管理连接和数…...
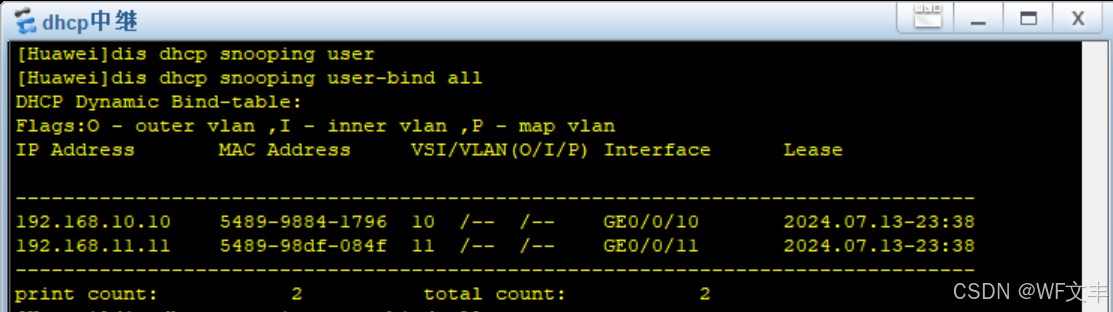
企业网络实验(vmware虚拟机充当DHCP服务器)所有IP全部保留,只为已知mac分配固定IP
文章目录 需求实验修改dhcp虚拟机配置文件测试PC获取IP查看user-bind 需求 (vmware虚拟机充当DHCP服务器)所有IP全部保留,只为已知mac分配固定IP 实验 前期配置: https://blog.csdn.net/xzzteach/article/details/140406092 后续配置均在以上配置的前…...
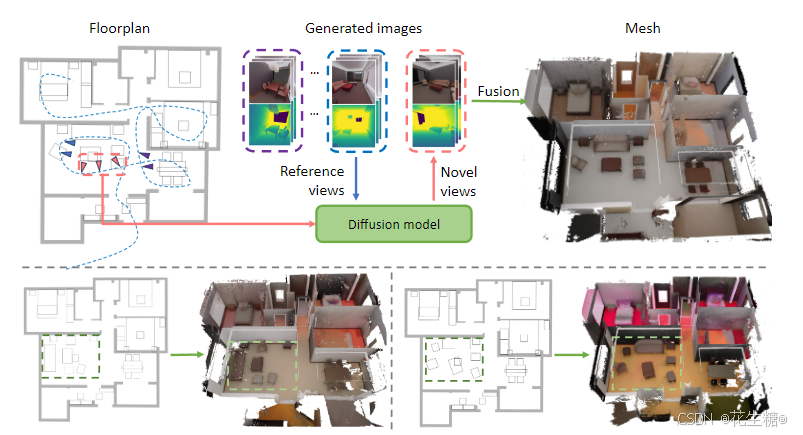
HouseCrafter:平面草稿至3D室内场景的革新之旅
在室内设计、房地产展示和影视布景设计等领域,将平面草稿图快速转换为立体的3D场景一直是一个迫切的需求。HouseCrafter,一个创新的AI室内设计方案,正致力于解决这一挑战。本文将探索HouseCrafter如何将这一过程自动化并提升至新的高度。 一、定位:AI室内设计的革新者 Ho…...
C#统一委托Func与Action
C#在System命名空间下提供两个委托Action和Func,这两个委托最多提供16个参数,基本上可以满足所有自定义事件所需的委托类型。几乎所有的 事件 都可以使用这两个内置的委托Action和Func进行处理。 Action委托: Action定义提供0~16个参数&…...

MongoDB 基本查询语句
基本查询 查询所有文档: db.collection.find()示例: db.users.find()按条件查询文档: db.collection.find({ key: value })示例: db.users.find({ age: 25 })查询并格式化输出: db.collection.find().pretty()示例&…...
28_EfficientNetV2网络详解
V1:https://blog.csdn.net/qq_51605551/article/details/140487051?spm1001.2014.3001.5502 1.1 简介 EfficientNetV2是Google研究人员Mingxing Tan和Quoc V. Le等人在2021年提出的一种深度学习模型,它是EfficientNet系列的最新迭代,旨在提…...

PyCharm查看文件或代码变更记录
背景: Mac笔记本上有一个截图的定时任务在运行,本地Python使用的是PyCharm IDE,负责的同事休假,然后定时任务运行的结果不符合预期,一下子不知道问题出现在哪里。 定位思路: 1、先确认网络、账号等基本的…...

Java开发手册中-避免Random实例被多线程使用、多线程下Random与ThreadLoacalRandom性能对比
场景 Java中使用JMH(Java Microbenchmark Harness 微基准测试框架)进行性能测试和优化: Java中使用JMH(Java Microbenchmark Harness 微基准测试框架)进行性能测试和优化_java热点函数-CSDN博客 参考以上性能测试工具的使用。 Java开发手册中有这样一条…...
【Arduino IDE】安装及开发环境、ESP32库
一、Arduino IDE下载 二、Arduino IDE安装 三、ESP32库 四、Arduino-ESP32库配置 五、新建ESP32-S3N15R8工程文件 乐鑫官网 Arduino官方下载地址 Arduino官方社区 Arduino中文社区 一、Arduino IDE下载 ESP-IDF、MicroPython和Arduino是三种不同的开发框架,各自适…...
【C++开源】GuiLite:超轻量UI框架-入门
开发环境说明 使用visual Studio 2022进行开发 下载源码 从如下的网址进行源码和示例代码的下载: GitHub源码网址为:idea4good/GuiLite示例代码路径为:idea4good/GuiLiteExample使用方法 GuiLite是一个仅有头文件的一个库,使用的时候直接include到自己的UIcode.cpp文件…...
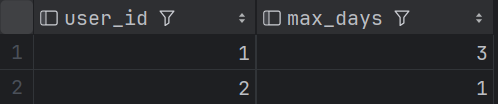
SQL面试题练习 —— 查询每个用户最大连续登录天数
目录 1 题目2 建表语句3 题解 1 题目 查询每个用户最大连续登录天数 样例数据如下 login_log: 2 建表语句 --建表语句 create table if not exists login_log (user_id int comment 用户id,login_time date comment 登录时间 ); --数据插入 INSERT overwrit…...
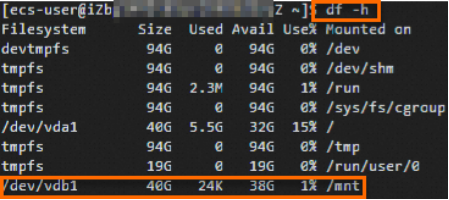
服务器系统盘存储不够,添加数据盘并挂载(阿里云)
目录 1.获取数据盘设备名称 2.为数据盘创建分区 3.为分区创建文件系统 4.配置开机自动挂载分区 阿里云数据盘挂载说明链接:在Linux系统中初始化小于等于2 TiB的数据盘_云服务器 ECS(ECS)-阿里云帮助中心 1.获取数据盘设备名称 sudo fdisk -lu 运行结果如下所示…...
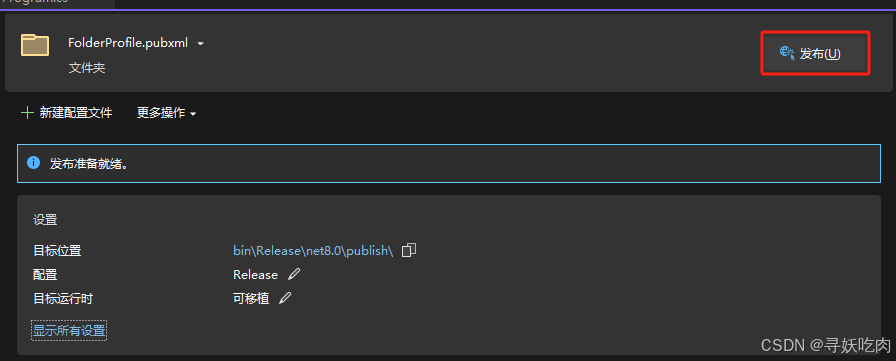
Visual Studio2022中使用.Net 8 在 Windows 下使用 Worker Service 创建守护进程
Visual Studio2022中使用.Net 8 在 Windows 下创建 Worker Service 1 什么是 .NET Core Worker Service1.1 确认Visual Studio中安装了 ASP.NET和Web开发2 创建 WorkerService项目2.1 新建一个WorkerService项目2.2 项目结构说明3 将应用转换成 Windows 服务3.1 安装Microsoft.…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...

华为云Flexus+DeepSeek征文 | 基于Dify构建具备联网搜索能力的知识库问答助手
华为云FlexusDeepSeek征文 | 基于Dify构建具备联网搜索能力的知识库问答助手 一、构建知识库问答助手引言二、构建知识库问答助手环境2.1 基于FlexusX实例的Dify平台2.2 基于MaaS的模型API商用服务 三、构建知识库问答助手实战3.1 配置Dify环境3.2 创建知识库问答助手3.3 使用知…...

【Axure高保真原型】图片列表添加和删除图片
今天和大家分享图片列表添加和删除图片的原型模板,效果包括: 点击图片列表的加号可以显示图片选择器,选择里面的图片; 选择图片后点击添加按钮,可以将该图片添加到图片列表; 鼠标移入图片列表的图片&…...

【Elasticsearch基础】Elasticsearch批量操作(Bulk API)深度解析与实践指南
目录 1 Bulk API概述 1.1 什么是批量操作 1.2 Bulk API的优势 2 Bulk API的工作原理 2.1 请求处理流程 2.2 底层机制 3 Bulk API的使用方法 3.1 基本请求格式 3.2 操作类型示例 3.3 响应格式 4 Bulk API的最佳实践 4.1 批量大小优化 4.2 错误处理策略 4.3 性能调…...

SpringSecurity+vue通用权限系统
SpringSecurityvue通用权限系统 采用主流的技术栈实现,Mysql数据库,SpringBoot2Mybatis Plus后端,redis缓存,安全框架 SpringSecurity ,Vue3.2Element Plus实现后台管理。基于JWT技术实现前后端分离。项目开发同时采 …...

Java多线程从入门到精通
一、基础概念 1.1 进程与线程 进程是指运行中的程序。 比如我们使用浏览器,需要启动这个程序,操作系统会给这个程序分配一定的资源(占用内存资源)。 线程是CPU调度的基本单位,每个线程执行的都是某一个进程的代码的某…...













