数据结构初阶·排序算法(内排序)
目录
前言:
1 冒泡排序
2 选择排序
3 插入排序
4 希尔排序
5 快速排序
5.1 Hoare版本
5.2 挖坑法
5.3 前后指针法
5.4 非递归快排
6 归并排序
6.1递归版本归并
6.2 非递归版本归并
7 计数排序
8 排序总结
前言:
目前常见的排序算法有9种,冒泡排序,选择排序,插入排序,希尔排序,快速排序,归并排序,计数排序,基数排序,桶排序。实际生活中排序的应用也是有限的,今天我们介绍其中7个,基数排序和桶排序不介绍。介绍常用的即可。
顺带一嘴,本文里面所有的排序都是内排序,也就是在内存里面进行排序的,还有一种排序叫做外排序,即是在磁盘里面进行排序的,这种排序具有记忆性,外排序用到的就是归并排序,因为归并排序有一个特点就是空间复杂度为O(N)。
好了正文开始。
1 冒泡排序

这个排序是排序中的老大哥了,不是说效率有多高,是因为一开始接触排序的同学绝对逃不开它哈哈。
冒泡排序的思想是两两比较,从而达到冒泡一趟可以确定一个数的位置,所以一趟下来需要的操作有两两比较,一趟就需要遍历整个数组,所以想要确定数组中所有元素的位置就需要两个循环,一个循环用来控制趟数,一趟循环用来控制两两比较。
我们排升序,一旦两两相邻的数满足条件,就交换两个变量的位置,基本思想确定了,现在来实现基本代码:
int arr[] = { 5,3,1,4,6,8,2,9,0,7 };
//冒泡排序
for (int i = 0; i < sizeof(arr) / sizeof(int); i++)
{for (int j = 0; j < sizeof(arr) / sizeof(int) - 1; j++){if (arr[j] > arr[j + 1]){swap(arr[j], arr[j + 1]);}}
}这就是最最基本的代码了,注意,这里的j < sizeof(arr) / sizeof(int) - 1的减一是一定要的,因为不减一是可能越界的,比如最后一个数不用冒泡了,但是没有减一就又冒了过去, + 1之后一下就越界了。
那么,我们在此基础上面如何进行修改呢?
我们知道,冒泡一趟可以确定一个数的位置,如果要排序10个数的位置,那么有没有必要冒泡10趟?没有吧,因为确定了9个数的位置最后一个数的位置自然而然就确定了,所以趟数可以进行修改,再来看第二个循环,一趟下来就确定了一个数的位置,那么最后1个或者n个数就不用冒泡了,因为我们知道它是已经排序好了的,那么一趟排好一个,我们就可以少冒泡一个,所以可以利用i进行循环次数的减少。
for (int i = 0; i < sizeof(arr) / sizeof(int) - 1; i++){for (int j = 0; j < sizeof(arr) / sizeof(int) - i - 1; j++){if (arr[j] > arr[j + 1]){swap(arr[j], arr[j + 1]);}}}那么我们还有没有修正空间呢?
有的,如果我们排序一个升序数组,但是该数组本身就是一个升序的数组,我们冒泡完一趟发现所有数都满足升序,就不想走后面的怎么办?这个时候我们就应该使用标志来确定一趟有没有交换,如果一趟没有交换,我们也就没有必要冒泡下去了:
for (int i = 0; i < sizeof(arr) / sizeof(int) - 1; i++){int flag = 0;for (int j = 0; j < sizeof(arr) / sizeof(int) - i - 1; j++){if (arr[j] > arr[j + 1]){swap(arr[j], arr[j + 1]);flag = 1;}}if (0 == flag)break;}这才是冒泡的最终形态,那么简单分析一下:
循环次数是一个标准的等差数列,所以时间复杂度为O(N^2);
空间复杂度方面,是没有新开空间的,所以空间复杂度为O(1)。
2 选择排序
选择排序顾名思义,通过选择来进行排序,我们选择的是最大最小值,再选择次大次小值,给他们安放到正确的位置上,从而完成排序:
这是选择排序的动图,是选择的最小值,但是我们今天实现的比这个高级一点点,我们今天实现的是双向选择,同时选择最大的和最小的,相对上面的来说并没有难度的增加,无非是代码加了一点而已。
选择排序的总体思想就是两边缩短,从现有的可访问区间里面选择最值,那么我们就需要控制区间,剩下的就是交换和选择最值了:
void SelectSort(int* arr,size_t size)
{int begin = 0, end = size - 1;while (begin < end){int mini = begin;int maxi = begin;//选择排序选择是区间 ->循环条件是区间for (int i = begin + 1; i <= end; i++){//找到最小的 记录下标if (arr[i] < arr[mini]){mini = i;}//找到最大的 记录下标if (arr[i] > arr[maxi]){maxi = i;}}swap(arr[begin], arr[mini]);//当max的值在最前面的时候 ->交换前已经冲突if (maxi == begin)maxi = mini;swap(arr[end], arr[maxi]);begin++, end--;}
}这里的begin和end是左闭右闭区间,所以在循环控制的时候就需要注意是i <= end,同时,我们相当于是在1 到下标为size - 1的数据,这里要是想要用i = begin开始遍历也可以,无非就是加了一条让自己和自己比较的语句,实际没必要,能减少循环次数咱们就减少。
那么有一个新问题,如果数组的最大值在数组下标为0的位置,那么最小元素就和最大值发生了交换,此时最大值的下标已经发生改变,我们再进行一轮的交换就不行,所以这里需要额外判断一下,防止maxi的值交换前变化。
时间复杂度方面,是一个标准的等差数列,也就是O(N^2),空间复杂度方面,没有多开空间,所以是O(1)。
3 插入排序

如果所示,是插入排序的动态演示。
单趟来看,就是把第n个数看成要插入的数据,再分别是前n - 1个数据进行比较,如果满足插入条件,就插入到相应位置,这里就需要一个临时变量来存储插入的数据,并且存在数据覆盖,那么整体来看,就是插入一个数据,把该数据之前的所有数据看成是有序的,即我们应该从前两个数据开始操作。
int end;
int tmp = arr[end + 1];
while (end >= 0)
{if (arr[end] > tmp){arr[end + 1] = arr[end];end--;}else{break;}
}
arr[end + 1] = tmp;这就是一个单趟,end + 1为插入数据,前end个数据都是要比较的元素,end >= 0也是因为下标为0的元素也需要比较。
那么插入排序就可以理解为,排序 [0,1],[0,2],[0,3]……[0,size- 1]区间,所以还需要一个循环用来控制end,好保证是区间一个一个排号的:
for (int i = 0; i < size - 1; i++)
{int end = i;int tmp = arr[end + 1];while (end >= 0){if (arr[end] > tmp){arr[end + 1] = arr[end];end--;}else{break;}}arr[end + 1] = tmp;
}这就是一个标准的插入排序,这个排序理解好之后,希尔排序才好理解,因为希尔就是在该排序的基础上进行修正的。
那么这个的时间复杂度和空间复杂度都很标准,是O(N^2),O(1)。
4 希尔排序

可以看到这里的动图和之前的动图有着不一样的点,即颜色不同,这里的颜色不同代表的是分的组别不同,即希尔将不同的元素按照一定的gap(间隔)分成了不同的组,那么问题来了,为什么要在插入排序的基础上加上分组这个思想呢?
原因是插入排序的最不理想的时候就是完全倒序的时候,这个时候基本上把循环吃满了,所以希尔就想,能不能先预排序一下,把所有的元素尽量的靠近最终的位置,所以分组排序,是一个预排序的过程,让数据尽量接近正确位置,预排序我们需要用到gap,即间隔,我们将间隔了gap的数据分为同一组,这一组数据里面进行排序,gap在排序的过程也在不断变化,那么为什么要变化呢?
这样想,gap = 1就是插入排序,就会好理解很多了。
所以现在我们要解决的第一个问题是,如何预排序,假设gap = 4,我们联想插入排序的时候,是gap = 1的排,那么现在无非就是间隔大了一点,所以只需略加修改:
int gap = 4;
int end = 0;
int tmp = arr[end + gap];
while (end >= 0)
{if (arr[end] > tmp){arr[end + gap] = arr[end];end -= gap;}else{break;}
}
arr[end + gap] = tmp;这是预排序了一组,现在就是,加循环,使每个组都预排序了,整个预排序就算是完成了:
for (int i = 0; i < gap; i++){for (int j = 0; j < size - gap; j++){int end = j;int tmp = arr[end + gap];while (end >= 0){if (arr[end] > tmp){arr[end + gap] = arr[end];end -= gap;}else{break;}}arr[end + gap] = tmp;}}这是最原始版本的预排序,是不是三层循环看着头都大了?最外层循环用来控制排序哪一组的,第二层循环,用来控制数组中该组的所有数据,内层就是进行排序,这种排序就太老实了,看着头大。
现在不难发现,gap不止是间隔,gap实际上是把所有的数据分为多少组,反正都是组内部相互排序了,我们每个组同时排不可以吗?
int gap = 4;
for (int i = 0; i < size - gap; i++)
{int end = i;int tmp = arr[end + gap];while (end >= 0){if (arr[end] > tmp){arr[end + gap] = arr[end];end -= gap;}else{break;}}arr[end + gap] = tmp;
}画一下图的话就会发现相当于是每个大区间的小区间依次排序,这样看着就不乱,那么预排序现在就做好了,我们现在就是考虑怎么从预排序变成最终排序?
那就很简单了,gap等于1就是最终排序,但是我们的gap也不能等于0,而且这个gap说法有挺多的,最后大部分结论是三等分数组,但是为了gap不能等于0,就会除3之后 + 1,只要让gap最终走到1但是不为0就可以:
int gap = size;
while (gap > 1)
{gap = gap / 3 + 1;for (int i = 0; i < size - gap; i++){int end = i;int tmp = arr[end + gap];while (end >= 0){if (arr[end] > tmp){arr[end + gap] = arr[end];end -= gap;}else{break;}}arr[end + gap] = tmp;}
}最终版本如上。
关于时间复杂度是很难计算的,主要是因为gap,这里就记住结论,O(N^1.3),空间复杂度是O(1)。
5 堆排序
堆排序就是老生常谈的知识了,因为向上建堆的时间复杂度是O(N * logN),向下建堆的时间复杂度是O(N - logN)即O(N),我们就采用向下建堆,最后呢,调整一下就没问题了,先来向下调整算法:
void AdjustDown(int* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size){if (child + 1 < size && a[child + 1] > a[child]){++child;}if (a[child] > a[parent]){swap(a[child], a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}然后开始建堆,建堆的思想很简单,如果每个堆都是很大堆,那么整个堆就是大堆了,所以我们从最后一个父节点开始调整,就有(size - 1 - 1 / 2)来找第一个父节点,随机调整每一个父节点:
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{AdjustDown(a, n, i);
}所以这就是建堆,然后就是调整交换了:
int end = n - 1;
while (end > 0)
{swap(a[0], a[end]);AdjustDown(a, end, 0);--end;
}时间复杂度标准的O(N * logN),空间复杂度为O(1);
6 快速排序
快速排序最初是由hoare发明的,简称为快排,既然敢叫快排就有它的厉害之处,快排的整体思想是将一个数一趟放到正确的位置,简单来说就是一趟下来,该数左边的数一定小于它,右边的数一定大于它,这里我们看个动图:
好吧没找到哈哈哈
那我描述一下,hoare版本是将左边第一个数据,即下标为0的元素选为key,然后有两个“东东”分别从首元素和末尾元素出发,因为我们排的是升序,所以精髓是在于右边的小东东先走,左东东找大,右东东找大小,直到右边的找到了比key小的就停下来,左边同理,找到比key大的就停下来,当两个都找到了,ok进行一次交换,这样相当于把一大一小换位,最后左右东东相遇的时候,就是key的正确位置,因为左右东东已经交换了来的路上的所有比key大的和比key小的,这样一趟下来,key的位置就是正确位置。
一趟下来我们就能确定一个数的正确位置,此时,数组被分为了三段,[begin,key - 1] key [key + 1,end],如果我们对最右边的区间在走一个单趟,还是会被分为三个区间,所以这里我们要用到的还有递归,遍历了根之后,然后遍历左子树右子树(二叉树乱入),这里就和二叉树挺像的了,这里其实就是前序遍历了。那么现在就来实现一下hoare版本吧。
6.1 Hoare版本
void QuickS(int* arr,int begin,int end)
{if (begin >= end)return;int keyi = begin;int left = begin, right = end;while (left < right){//右边找小while (left < right && arr[right] >= arr[keyi]){right--;}//左边找大while (left < right && arr[left] <= arr[keyi]){left++;}swap(arr[right], arr[left]);}swap(arr[keyi], arr[left]);keyi = left;QuickS(arr, begin, keyi - 1);QuickS(arr, keyi + 1, end);}霍尔版本就需要三个参数,因为我们对区间不停的排序,所以是arr,begin,end,然后对于为什么要赋值给left 和 right呢?因为最后的递归调用需要用到原来的begin和end,所以这里需要临时变量存储一下,当然有其他的存储方法,都是可以的。
然后是循环条件,最外while循环的循环条件没什么好说的,里层的while的循环条件是比较容易忘记的,因为里层的while循环条件也是要有left < left的,如果没有,那么一旦找不到就会死命的找,就会导致left > right的情况,其次,>= <= 的等于也是必要的,如果没有等于,left right 就会停在那里,导致原来要找的小的或者大的没有找到。
找到进行两次交换,最后就是两次区间递归,这里只要保证区间是对的,变量怎么取都可以,只要保证的是递归的那两个区间就行。
那么这里,提问为什么一定要右边先走?
因为要保证最后和arr[keyi]交换的位置是比keyi小的。
为什么右边相遇的位置一定是比arr[keyi]小的?
是因为右边先走,右边先走有两种相遇情况。
第一种是R遇见L,R没有找到小的,一直往L走,在此之前可能是R L都动过,所以L此时下面是一个比keyi小的数,相遇一定是比keyi小的,也可能是L没动过,那么R就可能是一直找到keyi自己,也是一种正确的情况。
第二种是L遇见R,R已经找到了小的,所以此时L遇见了R也肯定是遇见了一个比arr[keyi]小的数。
以上是快排的大部分易错点,后面的三个版本都是在单趟的基础上进行优化,我们就将单趟实现的不同函数分别写,最后调用函数,再递归,如下:
int PartSort1(int* arr, int begin, int end)
{//三数取中int midi = GetMidi(arr, begin, end);swap(arr[begin], arr[midi]);int left = begin, right = end;int key = begin;while (left < right){//右边找小while (arr[right] >= arr[key] && left < right){right--;}//左边找大while (arr[left] <= arr[key] && left < right){left++;}swap(arr[left], arr[right]);}swap(arr[left], arr[key]);return left;
}
void QuickSort(int* arr, int begin, int end)
{if (begin >= end)return;int key = PartSort1(arr, begin, end);QuickSort(arr, begin, key - 1);QuickSort(arr, key + 1, end);}这里可能还有一个疑问就是为什么keyi一定要取左边的,我取右边的不行吗?取两边都是可以的,取中间也可以,但是中间就麻烦一点,有的时候固执的取左边效率就比较低下,比如倒序的情况,这里的话我们就需要三数取中,也就是在左右中三个数取中间值的数来当keyi,这样好点,就和希尔的预排一样,有点类似,希尔是把数提前接近,这里是选择一个不用执行那么多语句的数来当keyi。三数取中就比较就可以了:
int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;// begin midi end 三个数选中位数if (a[begin] < a[midi]){if (a[midi] < a[end])return midi;else if (a[begin] > a[end])return begin;elsereturn end;}else // a[begin] > a[midi]{if (a[midi] > a[end])return midi;else if (a[begin] < a[end])return begin;elsereturn end;}
}但是但是,现在还有一个小问题就是,有的时候也存在杀鸡用牛刀的情况,比如我要对10000个数进行快排,剩余最后几个数的时候,我还是要一个个的去走递归,那就太麻烦了,我还不如选一个排序来完成接下来的排序呢,比如7个数我要递归7次,还是有点麻烦的,所以有的时候会这样:
//小区间优化版本
void QuickSort1(int* arr, int begin, int end)
{if (begin >= end)return;if (end - begin + 1 <= 10){//+begin是必要的InsertSort(arr + begin, end - begin + 1);}else{int midi = GetMidi(arr, begin, end);swap(arr[begin], arr[midi]);int left = begin, right = end;int key = begin;while (left < right){//右边找小while (arr[right] >= arr[key] && left < right){right--;}//左边找大while (arr[left] <= arr[key] && left < right){left++;}swap(arr[left], arr[right]);}swap(arr[left], arr[key]);QuickSort(arr, begin, left - 1);QuickSort(arr, left + 1, end);}
}还有10个数的时候我们调用其他排序,虽然但是效率提高了一点点,但是没有太多,所以我们了解一下就行。
6.2 挖坑法
接下来就是挖坑的介绍了,我们要先记住一个点就是,单趟快排的基本点就是让一个数到它正确的位置,那么怎么到正确的位置呢?即让左边的数小于它,右边的数大于它就行。基本思想是不变的。
挖坑的具体做法是这样的,将arr[keyi]存放到一个临时变量里面去,此时第一个坑位形成,即是arr[keyi],然后同样的,右边开始找小的,找到了,该数据给坑位,此时右边找到的位置就是一个坑位,左边同理,找到一个大的,给值,变坑位,最后左右相遇,就是keyi的正确位置了。
代码如下:
int PartSort2(int* arr, int begin, int end)
{//三数取中int midi = GetMidi(arr, begin, end);swap(arr[begin], arr[midi]);int key = arr[begin];int hole = begin;while (begin < end){//等于是必要的while (arr[end] >= key && begin < end){end--;}arr[hole] = arr[end];hole = end;while (arr[begin] <= key && begin < end){begin++;}arr[hole] = arr[begin];hole = begin;}arr[hole] = key;return hole;
}挖坑相对hoare版本的要理解多,但是总体思想是不变的。
6.3 前后指针法
前后指针的单趟思想也是没有变的,还是让一个数到它的正确位置上,不过这个到的过程可能有点差异而已,前后指针利用的是两个指针,指针prev最开始指向数组首元素,指针cur指向的是首元素的下一个位置,整个过程是,cur先走,判断该位置是否小于arr[keyi],小于的话,prev就跟上来,如果是大于的话,那么prev就在原地不动,当cur指向的位置再次小于arr[keyi],并且prev和cur之间隔着几个大的元素的时候,那么++prev之后交换cur指向的那个位置,重复这个过程即可,因为prev指向的就是比arr[keyi]小的位置,cur指向的是大的位置,交换则是为了最后正确位置做铺垫,最后的情况就是,prev和cur间隔的所有元素都比arr[keyi]大,此时prev的位置就是正确位置,交换prev的位置和arr[keyi]的位置即可完成一次单趟。
代码如下:
int QuickS(int* arr, int begin, int end)
{//三数取中int midi = GetMidi(arr, begin, end);swap(arr[begin], arr[midi]);int keyi = begin, prev = begin, cur = prev + 1;while (cur <= end){if (arr[cur] < arr[keyi] && ++prev != cur)swap(arr[prev], arr[cur]);cur++;}swap(arr[keyi], arr[prev]);return prev;
}第一步肯定是三数取中,然后是选定三个下标,分别是keyi,prev,cur,因为begin - end是左闭右闭区间,所以循环结束条件是cur <= end,判断条件这里可能看着有点复杂,第一个是判断是否小于arr[keyi],如果满足,那么++prev之后,不等于cur,就可以进行交换了,最后cur++,这里如果++prev != cur放在前面就不可以了,破坏了先决条件 arr[cur] < arr[keyi],所以顺序也是要注意的,最后就是交换,返回对应下标了。
6.4 非递归快排
前面使用递归快排的时候,不难发现递归的顺序是根,左子树,右子树,那么我们非递归快排的时候实现的也是这种顺序模式,但是我们不能用递归,就需要利用到其他数据结构了,这里呢用到的是栈,即我们将区间段存进去,排序好之后再返回一些区间段,反复该操作,那么我们该如果排序呢?前面已经封装好了单趟的排序,所以我们可以直接复用即可,这也是为什么要封装单趟排序。
对于栈的使用,我们只需要记住,不停进栈,出栈即可,所以整个排序模式下来就是:
进栈,出栈,排序,返回区间段,就可以了,代码如下:
void QuickNR(int* arr, int begin, int end)
{//栈不是用来存储数据的 存储的是区间stack<int> s;s.push(end);s.push(begin);while (!s.empty()){int left = s.top();s.pop();int right = s.top();s.pop();int keyi = QuickS(arr, left, right);if (left < keyi - 1){s.push(keyi - 1);s.push(left);}if (right > keyi + 1){s.push(keyi + 1);s.push(right);}}
}当栈为空的时候,也就是没有区间可以排序了,即所有区间都有序了,此时排序就完成了,先压begin还是end都是可以的,无非就是循环的top的顺序需要改一下。
快排的时间复杂度是O(N * logN),空间复杂度为O(logN);
7 归并排序
7.1递归版本归并
在前面介绍树的时候,介绍到过一道题,求总共的节点个数,具体做法就是整体二叉树看作是一个一个小的二叉树,从最低层的二叉树慢慢的归并上来,归并排序的思想和树的思想是一样的,我们不是要排序吗?那么我们排一个数的序,排序好了再排两个数的序,然后再是4个数排序,然后是8个数的排序,直到排完即可。
所以归并排序这里也是要用到递归的,递归到一个数的时候,就可以返回开始排序了,排序的时候我们是这样排的,两个数组成的集合已经有序,那么我们就两两比较,谁小谁就尾插即可,难就是难在如何递归上面:
void Merges(int* arr,int begin, int end, int* tmp)
{if (begin >= end)return;//递归int mid = (begin + end) / 2;Merges(arr, begin, mid, tmp);Merges(arr, mid + 1, end, tmp);//归并int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] <= arr[begin2]){tmp[i++] = arr[begin1++];}else{tmp[i++] = arr[begin2++];}}while (begin1 <= end1){tmp[i++] = arr[begin1++];}while (begin2 <= end2){tmp[i++] = arr[begin2++];}memcpy(arr + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}void MergeS(int* arr, int size)
{int* tmp = new int[size];Merges(arr,0,size - 1,tmp);delete[] tmp;
}
这里因为tmp的原因所以加了一个函数,当然也可以都写在一个函数里面,但是不太好控制,这里建议的就是分别写在两个函数。
归并的时间复杂度是O(N * logN),空间复杂度是O(N)。
7.2 非递归版本归并
同样,归并也有非递归版本,也就是左子树 右子树,根,递归那里,是从1 -> 2 -> 4 -> 8这样排序好的,也就是说我们非递归就是要直接实现这个过程,所以我们需要一个变量用来计算我们一次性要排序多少组,这里用到了gap,那么数组里面的每个gap组拍好了之后,gap就应该*2,重复这个过程就可以,那么越界的问题我们应该如何处理?
越界嘛,无非就是begin1 end1 begin2 end2出现了问题,那么如果是begin2 和 end1出现了问题直接break就可以了,因为已经排序完成,end2出现问题我们进行修正就可以了,begin1出问题?那基本不会的,所以,代码如下:
void MergeSortNonR(int* arr, int n)
{int* tmp = new int[sizeof(int) * n] {0};int gap = 1;while (gap < n){//整体排序 排序好了gap改变,模仿 1 -> 2 -> 4 -> 8for (size_t i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;//排序完成if (end1 >= n || begin2 >= n){break;}//后面部分差点意思if (end2 >= n){end2 = n - 1;}//开始归并int j = begin1;while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){tmp[j++] = arr[begin1++];}else{tmp[j++] = arr[begin2++];}}while (begin1 <= end1){tmp[j++] = arr[begin1++];}while (begin2 <= end2){tmp[j++] = arr[begin2++];}memcpy(arr + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;}delete[] tmp;
}8 计数排序
计数排序是很特殊的,因为它不是比较排序,往往排序的思想都是,比较谁大谁小再决定怎么操作,它不一样,它是通过数组的下标来排序的,计数排序的具体操作是先开空间,空间开多大呢?空间大小是排序的数集合的最大值减去最小值,所以排序有一个操作就是要找最大值最小值,其次就是,为什么要开这么大的空间?我只要最大的不行吗?也可以,但是空间浪费是很大的,比如排序 11101 99999,就会浪费10000多个空间,所以这里用到了相对映射。
空间开好了之后,就是用下标,判断每个下标对应的数字有多少,此时最小值就用上了,++之后,判断count下标对应的数字有多少,就赋值就行了。如下:
void Countsort(int* arr, int size)
{int max = arr[0];int min = arr[0];//找最值for (int i = 0; i < size; i++){if (arr[max] < arr[i])arr[max] = arr[i];if (arr[min] > arr[i])arr[min] = arr[i];}int* count = new int[(max - min + 1) * sizeof(int)] {0};for (int i = 0; i < size; i++){count[arr[i] - min]++;}int j = 0;for (int i = 0; i < max - min + 1; i++){while (count[i]--){arr[j++] = i + min;}}delete[] count;
}时间复杂度为O(N),空间复杂度为O(N),效率高得离谱。
9 排序总结
这里涉及稳定性的概念,稳定性是指相同的数,排序之后相对位置不变,所以这里直接给一张图了,自行体会了哦~

感谢阅读!
相关文章:

数据结构初阶·排序算法(内排序)
目录 前言: 1 冒泡排序 2 选择排序 3 插入排序 4 希尔排序 5 快速排序 5.1 Hoare版本 5.2 挖坑法 5.3 前后指针法 5.4 非递归快排 6 归并排序 6.1递归版本归并 6.2 非递归版本归并 7 计数排序 8 排序总结 前言: 目前常见的排序算法有9种…...

PL/SQL oracle上多表关联的一些记录
1.记录自己在PL/SQL上写的几张表的关联条件没有跑出来的一些优化 1. join后面跟上筛选条件 left join on t1.id t2.id and --- 带上分区字段,如 t1.month 202405, 操作跑不出来的一些问题,可能是数据量过大,未做分区过滤 2. 创建…...

Java.Net.UnknownHostException:揭开网络迷雾,解锁异常处理秘籍
在Java编程的浩瀚宇宙中,java.net.UnknownHostException犹如一朵不时飘过的乌云,让开发者在追求网络畅通无阻的道路上遭遇小挫。但别担心,今天我们就来一场说走就走的探险,揭秘这个异常的真面目,并手把手教你几招应对之…...

第十课:telnet(远程登入)
如何远程管理网络设备? 只要保证PC和路由器的ip是互通的,那么PC就可以远程管理路由器(用telnet技术管理)。 我们搭建一个下面这样的简单的拓扑图进行介绍 首先我们点击云,把云打开,点击增加 我们绑定vmn…...

【概率论三】参数估计:点估计(矩估计、极大似然法)、区间估计
文章目录 一. 点估计1. 矩估计法2. 极大似然法2.1. 似然函数2.2. 极大似然估计法 3. 评价估计量的标准3.1. 无偏性3.2. 有效性3.3. 一致性 二. 区间估计1. 区间估计的概念2. 正态总体参数的区间估计 参数估计讲什么 由样本来确定未知参数参数估计分为点估计与区间估计 一. 点估…...

自动化产线 搭配数据采集监控平台 创新与突破
自动化产线在现在的各行各业中应用广泛,已经是现在的生产趋势,不同的自动化生产设备充斥在各行各业中,自动化的设备会产生很多的数据,这些数据如何更科学化的管理,更优质的利用,就需要数据采集监控平台来完…...

【Karapathy大神build-nanogpt】Take Away Notes
B站翻译LINK Personal Note Andrej rebuild gpt2 in pytorch. Take Away Points Before entereing serious training, he use Shakespear’s work as a small debugging datset to see if a model can overfit. Overfitging is a should thing.If we use TF32 or BF32, (by…...

MySQL学习记录 —— 이십이 MySQL服务器日志
文章目录 1、日志介绍2、一般、慢查询日志1、一般查询日志2、慢查询日志FILE格式TABLE格式 3、错误日志4、二进制日志5、日志维护 1、日志介绍 中继服务器的数据来源于集群中的主服务。每次做一些操作时,把操作保存到重做日志,这样崩溃时就可以从重做日志…...
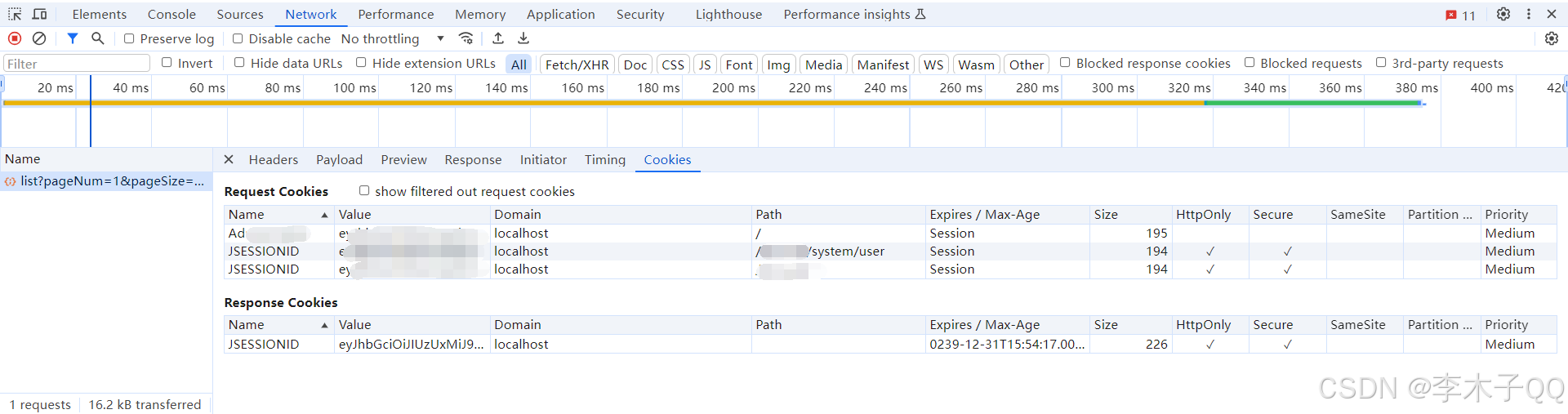
HTTPS请求头缺少HttpOnly和Secure属性解决方案
问题描述: 建立Filter拦截器类 package com.ruoyi.framework.security.filter;import com.ruoyi.common.core.domain.model.LoginUser; import com.ruoyi.common.utils.SecurityUtils; import com.ruoyi.common.utils.StringUtils; import com.ruoyi.framework.…...

react基础样式控制
行内样式 <div style{{width:500px, height:300px,background:#ccc,margin:200px auto}}>文本</div> class类名 注意:在react中使用class类名必须使用className 在外部src下新建index.css文件写入你的样式 .fontcolor{color:red } 在用到的页面引入…...
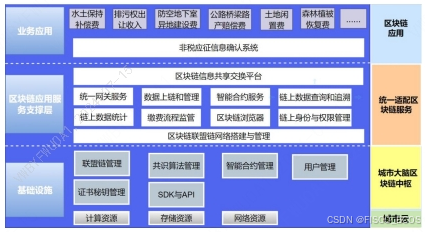
【区块链 + 智慧政务】涉税行政事业性收费“e 链通”项目 | FISCO BCOS应用案例
国内很多城市目前划转至税务部门征收的非税收入项目已达 17 项,其征管方式为行政主管部门核定后交由税务 部门征收。涉税行政事业性收费受限于传统的管理模式,缴费人、业务主管部门、税务部门、财政部门四方处于 相对孤立的状态,信息的传递靠…...

Socket、WebSocket 和 MQTT 的区别
Socket 协议 定义:操作系统提供的网络通信接口,抽象了TCP/IP协议,支持TCP和UDP。特点: 通用性:不限于Web应用,适用于各种网络通信。协议级别:直接使用TCP/UDP,需要手动管理连接和数…...
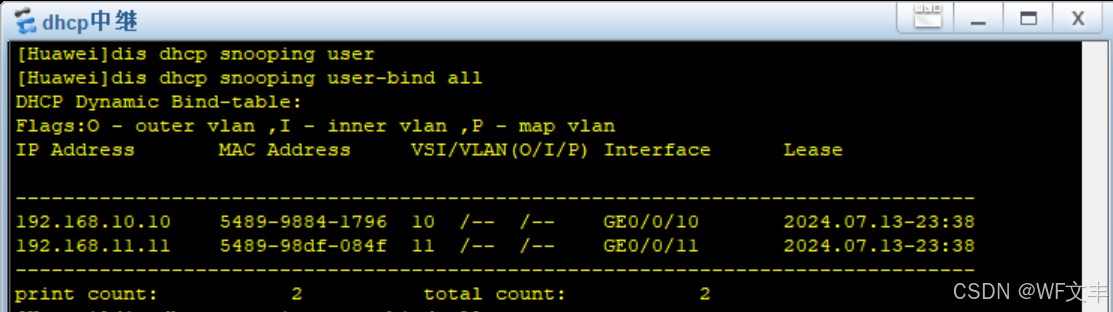
企业网络实验(vmware虚拟机充当DHCP服务器)所有IP全部保留,只为已知mac分配固定IP
文章目录 需求实验修改dhcp虚拟机配置文件测试PC获取IP查看user-bind 需求 (vmware虚拟机充当DHCP服务器)所有IP全部保留,只为已知mac分配固定IP 实验 前期配置: https://blog.csdn.net/xzzteach/article/details/140406092 后续配置均在以上配置的前…...
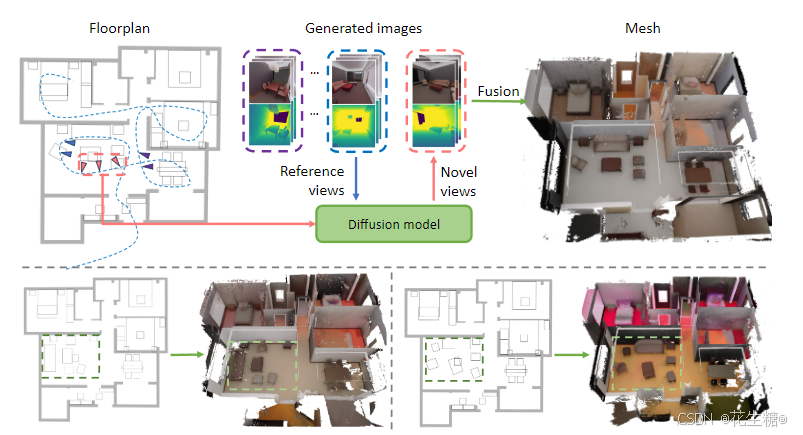
HouseCrafter:平面草稿至3D室内场景的革新之旅
在室内设计、房地产展示和影视布景设计等领域,将平面草稿图快速转换为立体的3D场景一直是一个迫切的需求。HouseCrafter,一个创新的AI室内设计方案,正致力于解决这一挑战。本文将探索HouseCrafter如何将这一过程自动化并提升至新的高度。 一、定位:AI室内设计的革新者 Ho…...
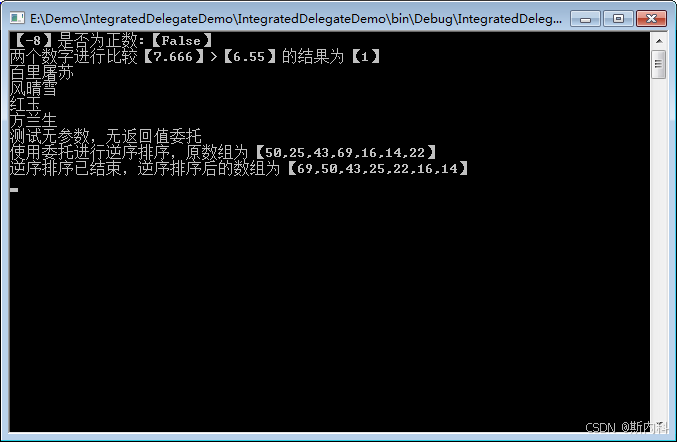
C#统一委托Func与Action
C#在System命名空间下提供两个委托Action和Func,这两个委托最多提供16个参数,基本上可以满足所有自定义事件所需的委托类型。几乎所有的 事件 都可以使用这两个内置的委托Action和Func进行处理。 Action委托: Action定义提供0~16个参数&…...

MongoDB 基本查询语句
基本查询 查询所有文档: db.collection.find()示例: db.users.find()按条件查询文档: db.collection.find({ key: value })示例: db.users.find({ age: 25 })查询并格式化输出: db.collection.find().pretty()示例&…...
28_EfficientNetV2网络详解
V1:https://blog.csdn.net/qq_51605551/article/details/140487051?spm1001.2014.3001.5502 1.1 简介 EfficientNetV2是Google研究人员Mingxing Tan和Quoc V. Le等人在2021年提出的一种深度学习模型,它是EfficientNet系列的最新迭代,旨在提…...

PyCharm查看文件或代码变更记录
背景: Mac笔记本上有一个截图的定时任务在运行,本地Python使用的是PyCharm IDE,负责的同事休假,然后定时任务运行的结果不符合预期,一下子不知道问题出现在哪里。 定位思路: 1、先确认网络、账号等基本的…...

Java开发手册中-避免Random实例被多线程使用、多线程下Random与ThreadLoacalRandom性能对比
场景 Java中使用JMH(Java Microbenchmark Harness 微基准测试框架)进行性能测试和优化: Java中使用JMH(Java Microbenchmark Harness 微基准测试框架)进行性能测试和优化_java热点函数-CSDN博客 参考以上性能测试工具的使用。 Java开发手册中有这样一条…...
【Arduino IDE】安装及开发环境、ESP32库
一、Arduino IDE下载 二、Arduino IDE安装 三、ESP32库 四、Arduino-ESP32库配置 五、新建ESP32-S3N15R8工程文件 乐鑫官网 Arduino官方下载地址 Arduino官方社区 Arduino中文社区 一、Arduino IDE下载 ESP-IDF、MicroPython和Arduino是三种不同的开发框架,各自适…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...
