100. 增减序列
给定一个长度为 n 的数列 a1,a2,…,an,每次可以选择一个区间 [l,r],使下标在这个区间内的数都加一或者都减一。
求至少需要多少次操作才能使数列中的所有数都一样,并求出在保证最少次数的前提下,最终得到的数列可能有多少种。
输入格式
第一行输入正整数 n。
接下来 n行,每行输入一个整数,第 i+1 行的整数代表 ai。
输出格式
第一行输出最少操作次数。
第二行输出最终能得到多少种结果。
数据范围
0<n≤105
0≤ai<2147483648输入样例:
4 1 1 2 2输出样例:
1 2
差分解决一段区域同时增加或减少的问题
给区间【L,R】上都加上一个常数c,则b[L] += c , b[R + 1] -=c求出a的差分序列b,其中b1 = a1,b(i) = a(i) - a(i - 1) (2 <= i <= n)。令b(n + 1) = 0,题目对序列a的操作,相当于每次可以选出b1,b2…b(n + 1)中的任意两个数,一个加1,另外一个减一。目标是把b2,b3,…bn变为全0。最终得到的数列a就是由 n 个 b1 构成的
任选两个数的方法可分为四类
1、2 <= i , j <=n(优先)
2、i = 1, 2 <=j <=n
3、2 <= i <= n , j = n + 1
4、i = 1, j = n + 1(没有意义)设b2,b3....bn中正数总和为p,负数总和的绝对值为q。首先以正负数匹配的方式尽量执行1类操作,可执行min(p,q)次。剩余|p - q|个为匹对,每个可以选与b1或b(n + 1)匹配,即执行2 或 3 类操作,共需|p - q|次
综上所诉,最少操作次数为min(p,q) + |p - q|。根据|p - q|次第2、3类操作的选择情况,能产生|p - q| + 1中不同的b1的值,即最终得到的序列a可能有|p - q| + 1 种
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
using namespace std;constexpr int N=1e5+7;
typedef long long ll;
ll n,a[N],b[N];
int main(){scanf("%lld",&n);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);b[i]=a[i]-a[i-1];}ll zheng=0, fu=0;for(int i=2;i<=n;i++) {if (b[i] > 0) {zheng += b[i];}else if (b[i] < 0) {fu -= b[i];}}ll ans1= max(zheng ,fu);ll ans2= abs(zheng-fu)+1;printf("%lld\n", ans1);printf("%lld\n", ans2);return 0;
}
相关文章:

100. 增减序列
给定一个长度为 n 的数列 a1,a2,…,an,每次可以选择一个区间 [l,r],使下标在这个区间内的数都加一或者都减一。 求至少需要多少次操作才能使数列中的所有数都一样,并求出在保证最少次数的前提下,最终得到的数列可能有多少种。 输入…...
操作系统之进程的初步认识(1)
进程1. 进程的相关概念1.1 进程的定义1.2 进程的概念(1)1.3 进程的概念(2)2. 进程和程序的区别3. 进程管理:3.1 进程的结构体有哪些属性(1) Pid(操作系统里指进程识别号)(2) 内存指针(3) 文件描述符表4. 进程调度:(1) 并行(2) 并发5. 进程调度需要的属性(1) 进程状态(2) 进程优…...

【Java】你真的懂封装吗?一文读懂封装-----建议收藏
博主简介:努力学习的预备程序媛一枚~博主主页: 是瑶瑶子啦所属专栏: Java岛冒险记【从小白到大佬之路】 前言 write in the front: 如何理解封装? 试想:我们使用微波炉的时候,只用设置好时间,按下“开始”…...

使用MobaXterm ssh远程登录Ubuntu 20.04
使用MobaXterm 远程登录Ubuntu 20.04 首先需要到官网下载一个MobaXterm 准备一台Ubuntu20.04的虚拟机。使用ifconfig查看IP 我这里的虚拟机是新安装的,所以会提示命令不存在,只要按照提示输入: sudo apt install net-tools接着等待安装完成…...
蓝桥杯历年真题训练
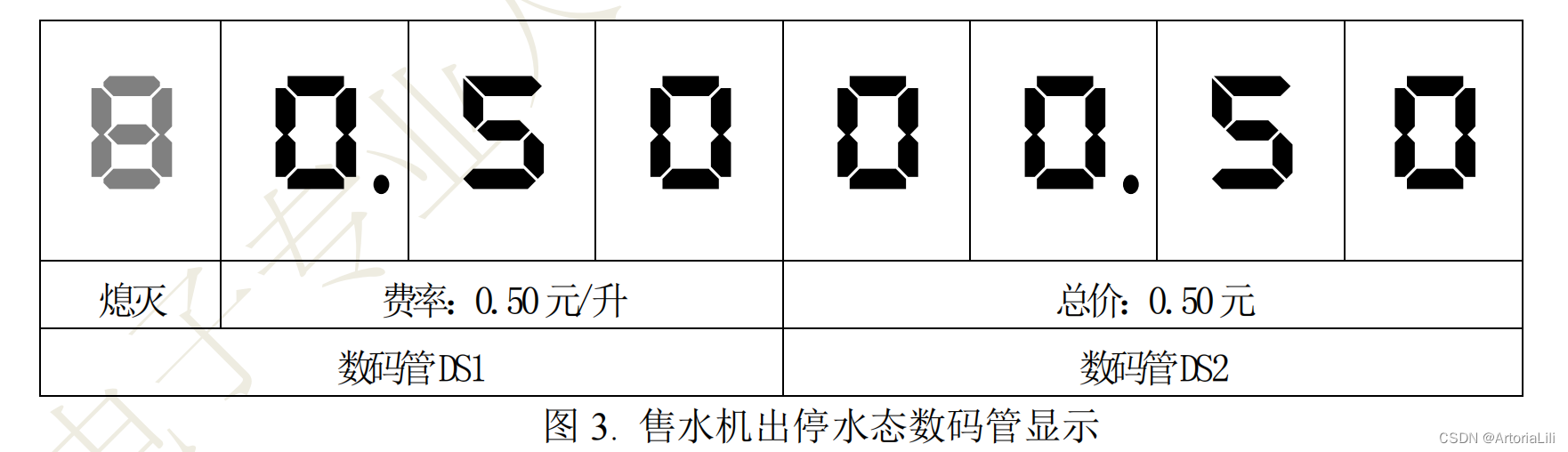
2012年第四届全国电子专业人才设计与技能大赛“自动售水机”设计任务书1. 系统框图接下来我们将任务分块: 1. 按键控制单元 设定按键 S7 为出水控制按键,当 S7 按下后,售水机持续出水(继电器接通,指示 灯 L10 点亮&…...

Spring事务报错: org.springframework.transaction.UnexpectedRollbackException
异常信息:支持当前事务,如果不存在则抛出异常。事务被回滚,因为它被标记为仅回滚 org.springframework.transaction.UnexpectedRollbackException: Transaction rolled back because it has been marked as rollback-onlyat org.springframe…...
Spring:IOC和AOP
Spring:IOC和AOP一. IOC(1) 引入(2) 定义(3) 作用(4) 实现(5) DI依赖注入二. AOP(1) 概念(2) Spring中的AOP(3) 入门案例0. 准备:1. 定义通知类和通知方法;2. 在通知类中描述和定义切入点 pointcut3. 用注释绑定切入点和通知方法4. 通知类&am…...

【笔记】效率之门——Python中的函数式编程技巧
文章目录Python函数式编程1. 数据2. 推导式3. 函数式编程3.1. Lambda函数3.2. python内置函数3.3. 高阶函数4. 函数式编程的应用Python函数式编程 我的AI Studio项目:【笔记】LearnDL第三课:Python高级编程——抽象与封装 - 飞桨AI Studio (baidu.com) p…...
Java【多线程基础2】 Thread类 及其常用方法
文章目录前言一、Thread类1, 构造方法2, 常用成员属性3, 常用成员方法3.1, start 启动线程3.2, interrupt 中断线程 (重点)3.2.1, 手动设置标记位3.2.2, 使用内置标记位3.3.3, interrupt 方法 的作用3.3 sleep 休眠线程3.4, jion 等待线程3.5 获取当前线程的引用总结前言 各位读…...

JVM调优实战及常量池详解
目录 阿里巴巴Arthas详解 Arthas使用场景 Arthas使用 GC日志详解 如何分析GC日志 CMS G1...
ChatGPT研究分析:GPT-4做了什么
前脚刚研究了一轮GPT3.5,OpenAI很快就升级了GPT-4,整体表现有进一步提升。追赶一下潮流,研究研究GPT-4干了啥。本文内容全部源于对OpenAI公开的技术报告的解读,通篇以PR效果为主,实际内容不多。主要强调的工作…...

我为什么要写博客,写博客的意义是什么??
曾经何时我也不知道,怎样才能变成我自己所羡慕的大佬!!在一次次的CSDN阅读的过程中,结实了许多志同道合的人!!包过凉哥,擦姐……大佬,但是,很遗憾,与这些人只…...
ssm框架之spring:浅聊AOP
AOP(Aspect Oriented Programming),是一种设计思想。先看一下百度百科的解释: 在软件业,AOP为Aspect Oriented Programming的缩写,意为:面向切面编程,通过预编译方式和运行期间动态…...

k8s详解
一、k8s中的yaml文件 JSON格式:主要用于api接口之间信息的传递YAML格式:主要用于配置和管理,YAML是一种简洁的非标记性语言,内容格式人性化 YAML格式: 大小写敏感使用缩进代表层级关系,不支持TAB制表符缩…...
第一章操作系统引论 1.1操作系统的目标和作用)
计算机操作系统(第四版)第一章操作系统引论 1.1操作系统的目标和作用
第一章操作系统引论 1.1操作系统的目标和作用 什么是操作系统OS? 配置在计算机硬件上的第一层软件是对硬件的首次扩充。 是最重要的系统软件,其他系统软件应用软件都依赖于操作系统的支持。 操作系统主要作用? 管理计算机系统所有硬件设…...
)
git push解决办法: ! [remote rejected] master -> master (pre-receive hook declined)
项目经理远程创建了一个空项目,无任何内容,给我赋予的developer账号权限,本地改为后提交代码试了很多次都上传不上去,报错如下: ! [remote rejected] master -> master (pre-receive hook declined)先说结果&#x…...
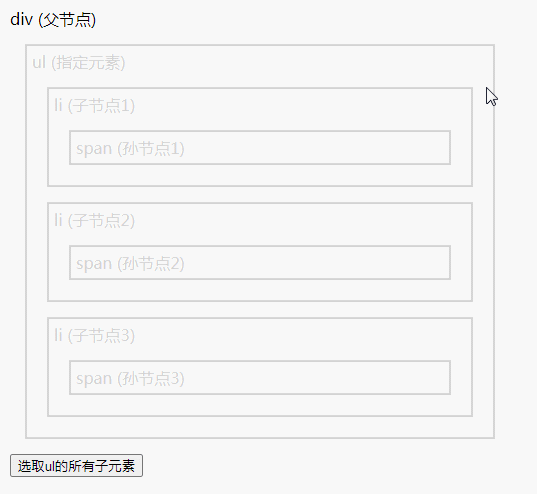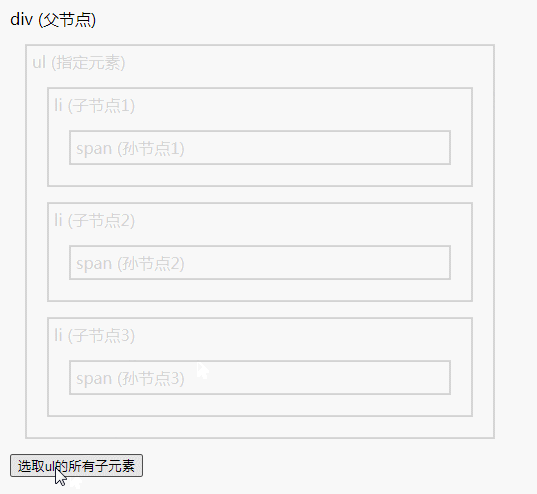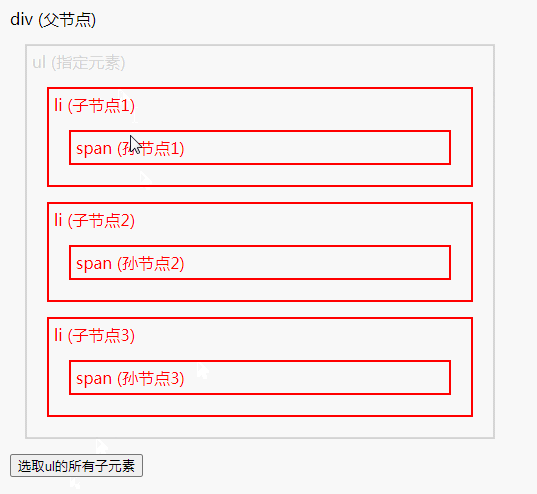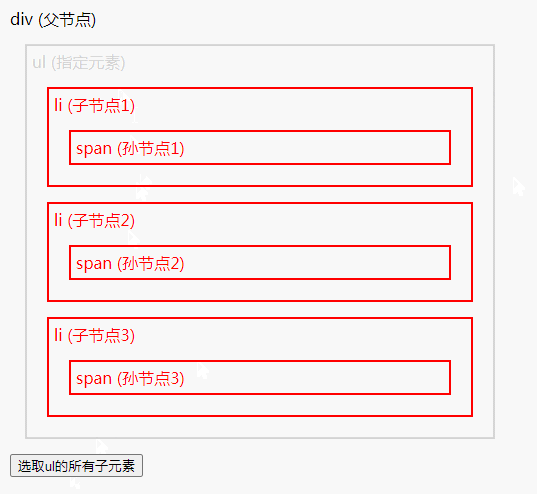
jQuery 遍历方法总结
遍历方法有:1、add(),用于把元素添加到匹配元素的集合中;2、children(),用于返回被选元素的所有直接子元素;3、closest(),用于返回被选元素的第一个祖先元素;4、contents(),用于返回…...
拦截器)
OKHttp 源码解析(二)拦截器
游戏SDK架构设计之代码实现——网络框架 OKHttp 源码解析(一) OKHttp 源码解析(二)拦截器 前言 上一篇解读了OKHttp 的基本框架源码,其中 OKHttp 发送请求的核心是调用 getResponseWithInterceptorChain 构建拦截器链…...
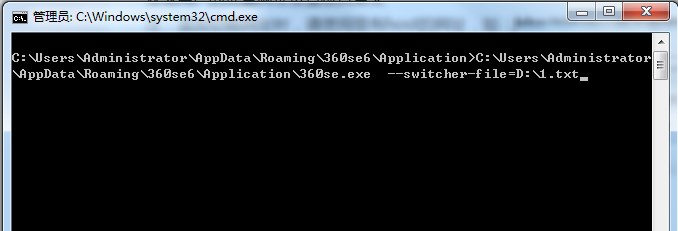
如何修改设置浏览器内核模式
优先级: 强制锁定极速模式 >手动切换(用户)>meta指定(开发者)>浏览器兼容列表(浏览器) 需要用360安全浏览器14,chromium108内核,下载地址https://bbs.360.cn/t…...

30个Python常用小技巧
1、原地交换两个数字 1 2 3 4 x, y 10, 20 print(x, y) y, x x, y print(x, y) 10 20 20 10 2、链状比较操作符 1 2 3 n 10 print(1 < n < 20) print(1 > n < 9) True False 3、使用三元操作符来实现条件赋值 [表达式为真的返回值] if [表达式] else [表达式…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...
