HarmonyOS ArkUi @CustomDialog 和promptAction.openCustomDialog踩坑以及如何选择
@CustomDialog 内使用@Link,如何正常使用
- 错误使用方式:
定义一个函数,在函数内使用弹窗,如下面代码showDialog:
这种使用方式,无法在自定义的@CustomDialog内使用 @Link,进行父子双向绑定,会报错:
Error message:is not callable
下面这种写法有可能是 this指向问题,个人猜测的
showDialog(tabIndex: number) {this.controller = new CustomDialogController({builder: RadioDialog({curTabIndex: tabIndex,tabList: this.tabArr, }),});this.controller.open()}
- 正确使用:
需要再build下使用
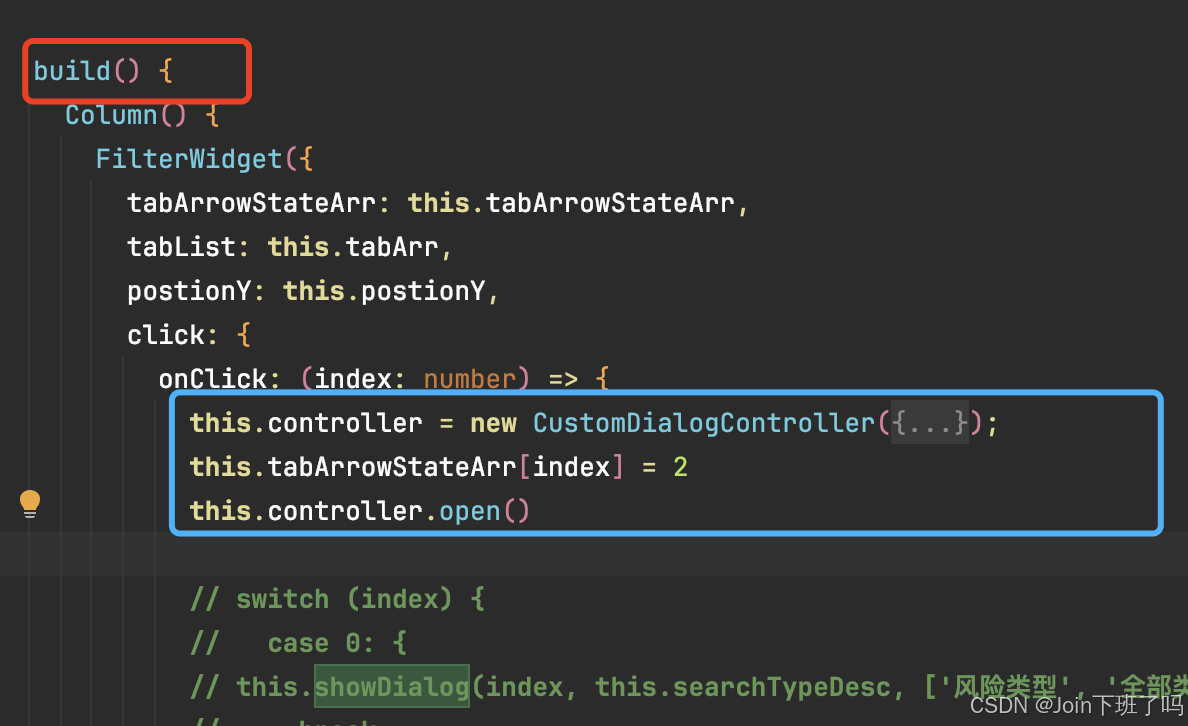
promptAction.openCustomDialog
此种方式,无法全屏(DIalog本身内容全屏),状态栏和导航条盖不住
即使设置很大的高度也只能导航条能遮住,除非偏移量设置负数,
但是这种使用太傻逼了
目前找其他人进行测试也不行,也许可能本身就不支持全屏吧。
目前给华为提了工单,华为的回复就是promptAction.openCustomDialog :此方式不支持全屏
如何选择
如果需要DIalog内容区域需要全屏的话选择 @CustomDialog,
一些简单的,后续也不会有全屏的需求的可以使用 promptAction.openCustomDialog
相关文章:

HarmonyOS ArkUi @CustomDialog 和promptAction.openCustomDialog踩坑以及如何选择
CustomDialog 内使用Link,如何正常使用 错误使用方式: 定义一个函数,在函数内使用弹窗,如下面代码showDialog: 这种使用方式,无法在自定义的CustomDialog内使用 Link,进行父子双向绑定&#x…...

Python面试题:详细讲解Python的多线程与多进程编程问题
在 Python 中,多线程和多进程编程是并发编程的两种主要方式,用于提高程序的执行效率和响应性。虽然它们都可以实现并发执行,但它们的工作原理和适用场景有所不同。以下是对 Python 多线程和多进程编程的详细讲解,包括它们的工作原…...
前端Canvas入门——用canvas写五子棋?
前言 五子棋的实现其实不难,因为本身就是一个很小的游戏。 至于画线什么的,其实很简单,都是lineTo(),moveTo()就行了。 难的在于——怎么让棋子落入到指定的格子上,怎么判断连子胜利。 当然啦,这部分是…...

[PaddlePaddle飞桨] PaddleDetection-通用目标检测-小模型部署
PaddleDetection的GitHub项目地址 推荐环境: PaddlePaddle > 2.3.2 OS 64位操作系统 Python 3(3.5.1/3.6/3.7/3.8/3.9/3.10),64位版本 pip/pip3(9.0.1),64位版本 CUDA > 10.2 cuDNN > 7.6pip下载指令: python -m pip i…...

Golang | Leetcode Golang题解之第239题滑动窗口最大值
题目: 题解: func maxSlidingWindow(nums []int, k int) []int {n : len(nums)prefixMax : make([]int, n)suffixMax : make([]int, n)for i, v : range nums {if i%k 0 {prefixMax[i] v} else {prefixMax[i] max(prefixMax[i-1], v)}}for i : n - 1…...

深度解析:在 React 中实现类似 Vue 的 KeepAlive 组件
在前端开发中,Vue 的 keep-alive 组件是一个非常强大的工具,它可以在组件切换时缓存组件的状态,避免重新渲染,从而提升性能。那么,如何在 React 中实现类似的功能呢?本文将带你深入探讨,并通过代…...

2024-7-20 IT新闻
目录 微软全球IT系统故障 中国量子计算产业峰会召开 其他IT相关动态 微软全球IT系统故障 后续处理: 微软和CrowdStrike均迅速响应,发布了相关声明并部署了修复程序。CrowdStrike撤销了有问题的软件更新,以帮助用户恢复系统正常运作。微软也…...
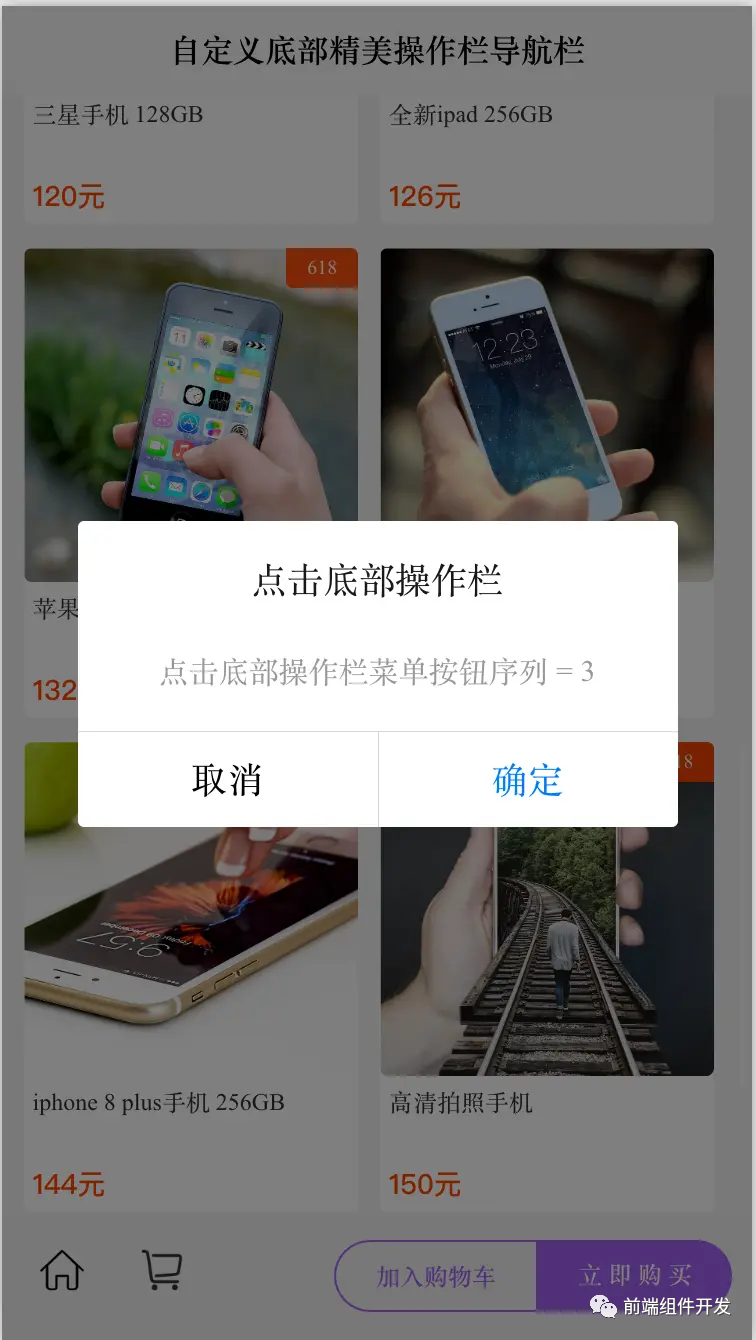
前端组件化开发:以Vue自定义底部操作栏组件为例
摘要 随着前端技术的不断演进,组件化开发逐渐成为提升前端开发效率和代码可维护性的关键手段。本文将通过介绍一款Vue自定义的底部操作栏组件,探讨前端组件化开发的重要性、实践过程及其带来的优势。 一、引言 随着Web应用的日益复杂,传统的…...

11.斑马纹列表 为没有文本的链接设置样式
斑马纹列表 创建一个背景色交替的条纹列表。 使用 :nth-child(odd) 或 :nth-child(even) 伪类选择器,根据元素在一组兄弟元素中的位置,对匹配的元素应用不同的 background-color。 💡 提示:你可以用它对其他 HTML 元素应用不同的样式,如 <div>、<tr>、<p&g…...

【算法】跳跃游戏II
难度:中等 题目: 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处: 0 < j < nums[…...
学习大数据DAY20 Linux环境配置与Linux基本指令
目录 Linux 介绍 Linux 发行版 Linux 和 Windows 比较 Linux 就业方向: 下载 CentOS Linux 目录树 Linux 目录结构 作业 1 常用命令分类 文件目录类 作业 2 vim 编辑文件 作业 3 你问我第 19 天去哪了?第 19 天在汇报第一阶段的知识总结,没什…...

达梦+flowable改造
原项目springbootflowablemysql模式现需改造springbootflowable达梦, 1.在项目中引入达梦jpa包 引入高版本包已兼容flowable(6.4.2)liquibase(3.6.2) 我没有像网上做覆盖及达梦配置 <dependency> …...

【乐吾乐2D可视化组态编辑器】消息
消息 乐吾乐2D可视化组态编辑器demo:https://2d.le5le.com/ 监听消息 const fn (event, data) > {}; meta2d.on(event, fn);// 监听全部消息 meta2d.on(*, fn);// 取消监听 meta2d.off(event, fn); meta2d.off(*, fn); Copy 系统消息 event(…...
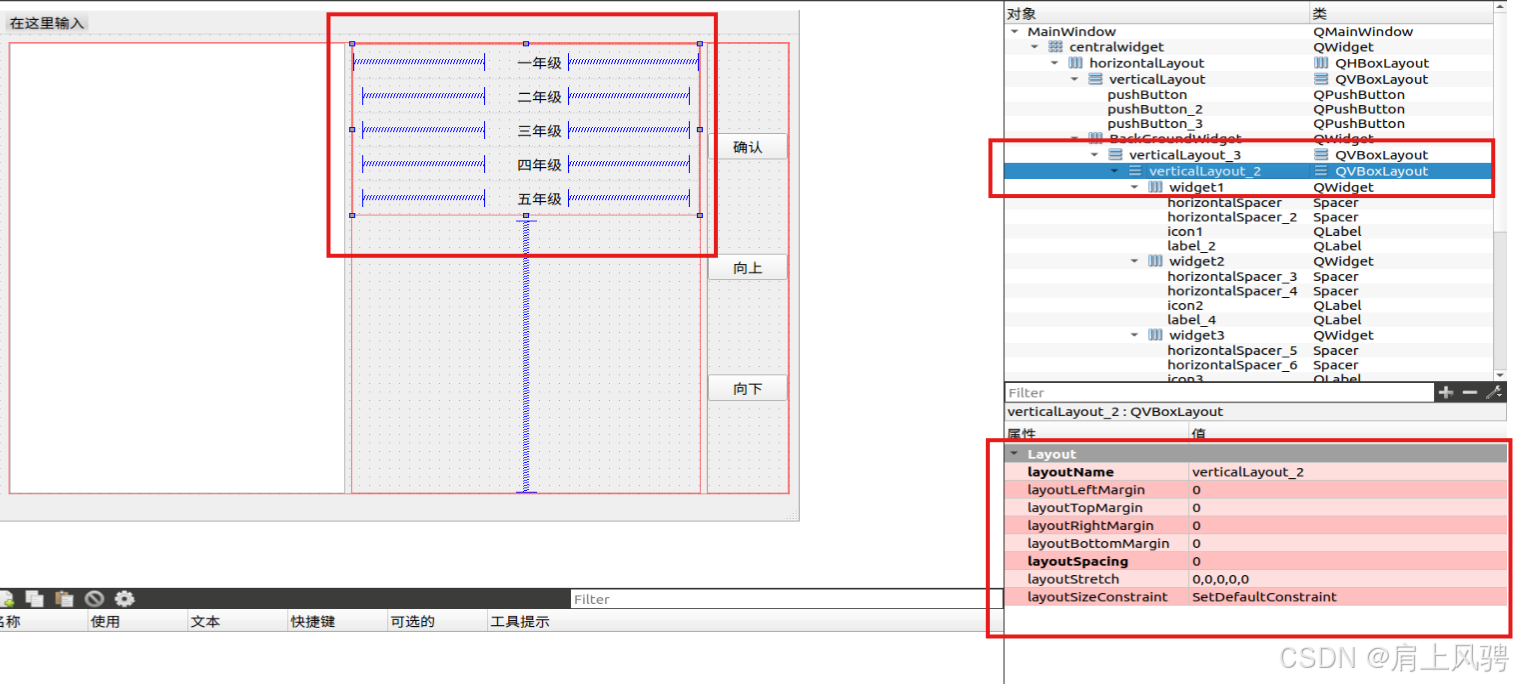
Qt创建列表,通过外部按钮控制列表的选中下移、上移以及左侧图标的显现
引言 项目中需要使用列表QListWidget,但是不能直接拿来使用。需要创建一个列表,通过向上和向下的按钮来向上或者向下移动选中列表项,当当前项背选中再去点击确认按钮,会在列表项的前面出现一个图标。 实现效果 本实例实现的效果如下: 实现思路 思路一 直接采用QLis…...

svn不能记住密码,反复弹出GNOME,自动重置svn.simple文件
1. 修改文件 打开 ~/.subversion/auth/svn.simple/xxx 更新前 K 15 svn:realmstring V 32 xxxxx //svn 地址,库的地址 K 8 username V 4 xxx //用户名 END在顶部插入下面内容, 注意,如果密码不对,则文件文法正常生效 更新后…...
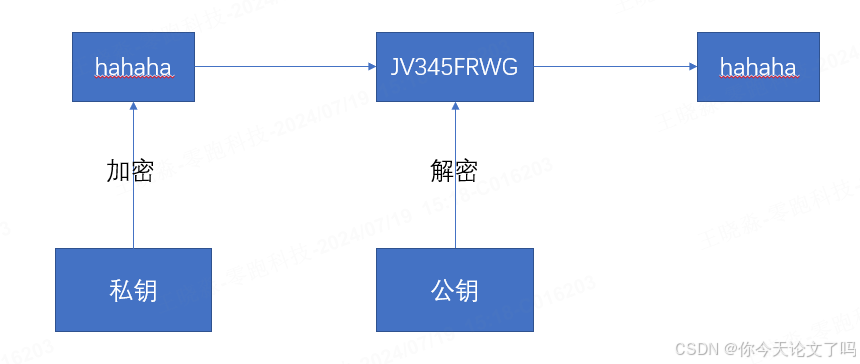
对称加密与非对称加密
对称加密 对称加密指的是加密和解密使用同一个秘钥,所以叫对称加密。对称加密只有一个秘钥,称为私钥。 优点:算法公开、计算量小、加密速度快、效率高 缺点:数据传输前,发送方和接收方必须确定好秘钥,双方也必须要保存好秘钥。 常见对称加密算法: DES、3DES、AES、3…...

03 Git的基本使用
第3章:Git的基本使用 一、创建版本仓库 一)TortoiseGit 选择项目地址,右键,创建版本库 初始化git init版本库 查看是否生成.git文件(隐藏文件) 二)Git 选择项目地址,…...
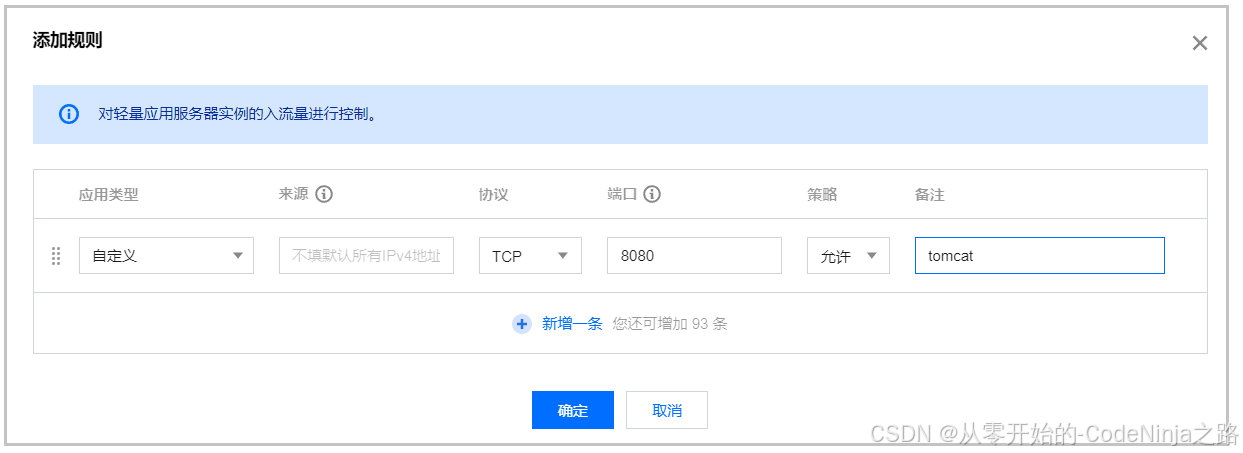
【Linux】将IDEA项目部署到云服务器上,让其成为后台进程(保姆级教学,满满的干货~~)
目录 部署项目到云服务器什么是部署一、 创建MySQL数据库二、 修改idea配置项三、 数据打包四、 部署云服务器五、开放端口号六 、 验证程序 部署项目到云服务器 什么是部署 ⼯作中涉及到的"环境" 开发环境:开发⼈员写代码⽤的机器.测试环境:测试⼈员测试程序使⽤…...
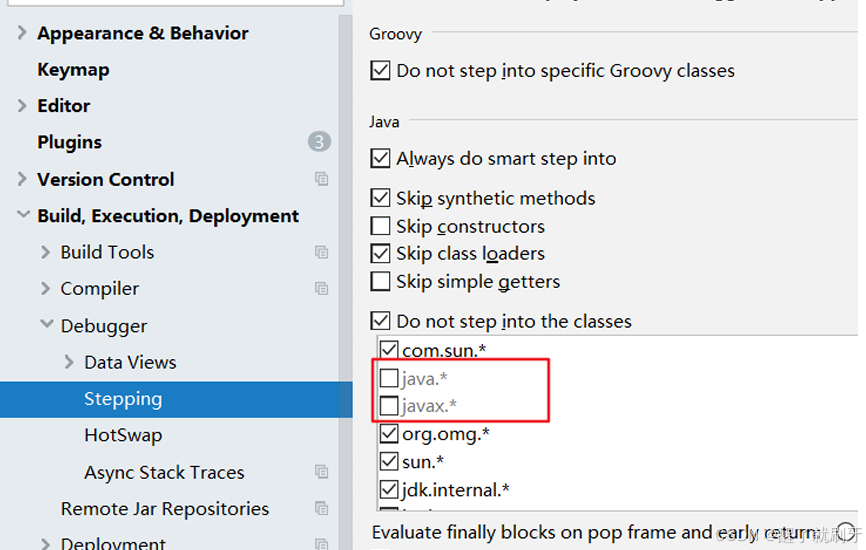
IDEA的断点调试(Debug)
《IDEA破解、配置、使用技巧与实战教程》系列文章目录 第一章 IDEA破解与HelloWorld的实战编写 第二章 IDEA的详细设置 第三章 IDEA的工程与模块管理 第四章 IDEA的常见代码模板的使用 第五章 IDEA中常用的快捷键 第六章 IDEA的断点调试(Debug) 第七章 …...

部署django
部署Django项目到Apache HTTP服务器上,通常会使用mod_wsgi模块,这是Apache的一个扩展,专为Python web应用设计,可以很好地与Django集成。以下是部署Django项目的简要步骤: 准备工作 确保环境准备就绪: 确保你的系统中已安装了Python、Django以及Apache HTTP Server。安装…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
