凸优化学习:PART3凸优化问题(持续更新)
凸优化问题
凸优化问题的广义定义:
- 目标函数为凸函数
- 约束集合为凸集
一、优化问题
基本用语
一般优化问题的描述:
minimizef0(x)subject to fi(x)⩽0,i=1,⋯,mhi(x)=0,i=1,⋯,p(1)\begin{array}{ll} \operatorname{minimize} & f_0(x) \\ \text { subject to } & f_i(x) \leqslant 0, \quad i=1, \cdots, m \\ & h_i(x)=0, \quad i=1, \cdots, p \end{array}\tag{1} minimize subject to f0(x)fi(x)⩽0,i=1,⋯,mhi(x)=0,i=1,⋯,p(1)
相关定义:
x∈Rnx\in \R^nx∈Rn:优化变量,optimization variable
f0:Rn→Rf_0:\R^n\rightarrow Rf0:Rn→R:目标函数/损失函数,objective function/cost function
若是一个极大化问题,那么称为 效用函数 utility function
fi(x)≤0:Rn→Rf_i(x)\leq 0:\R^n\rightarrow \Rfi(x)≤0:Rn→R:不等式约束,inequality constraint
hi(x)=0h_i(x)=0hi(x)=0:等式约束 equality constraint
m=p=0m=p=0m=p=0:无约束 unconstraited
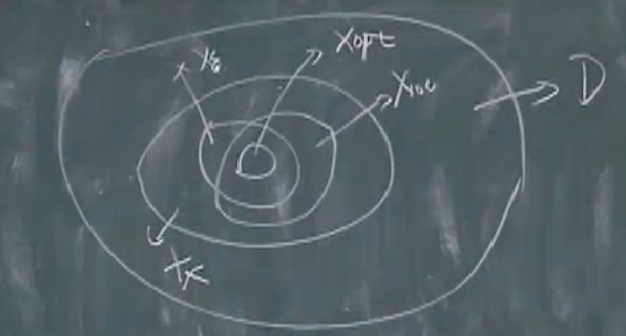
优化问题的域:domain;所有函数定义域的交集
D=⋂i=0mdomfi∩⋂i=1pdomhi\mathcal{D}=\bigcap_{i=0}^m \operatorname{dom} f_i \cap \bigcap_{i=1}^p \operatorname{dom} h_i D=i=0⋂mdomfi∩i=1⋂pdomhi
可行解集:feasible set,使得问题约束满足的解的集合
注意,还需要在目标函数的定义域内
最优点与局部最优点
最优点与局部最优点:若可行解集合不是空集那么总是能在集合中找到一个X,使得目标函数最优,这个值称为最优值。
P∗=inf{f0(x)∣X∈Xf}P^*=\inf \{f_0(x)|X\in X_f\} P∗=inf{f0(x)∣X∈Xf}
若XfX_fXf为空集,那么P∗=∞P^*=\inftyP∗=∞
最优解:若X∗X^*X∗可行,且f0(X∗)=P∗f_0(X^*)=P^*f0(X∗)=P∗
最优解集:最优解的集合
Xopt={X∣X∈Xf,f0(X)=P∗}X_{opt}=\{X|X\in X_f,f_0(X)=P^*\} Xopt={X∣X∈Xf,f0(X)=P∗}
ϵ−\epsilon-ϵ−次优解集:satisficing solution

约束一般要满足,目标函数值不一定要达到最优值,可以离最优值小一定的距离ϵ\epsilonϵ
Xϵ={X∈Xf,f0(X)≤P∗+ϵ}X_{\epsilon}=\{X\in X_f,f_0(X)\leq P^*+\epsilon\} Xϵ={X∈Xf,f0(X)≤P∗+ϵ}
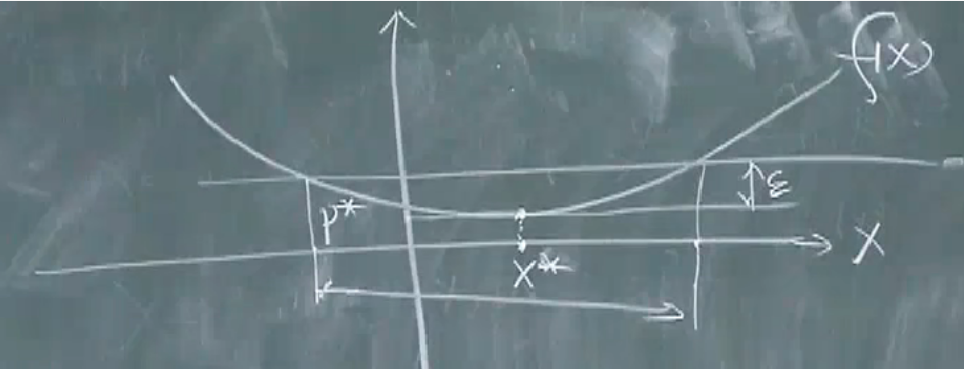
局部最优解:
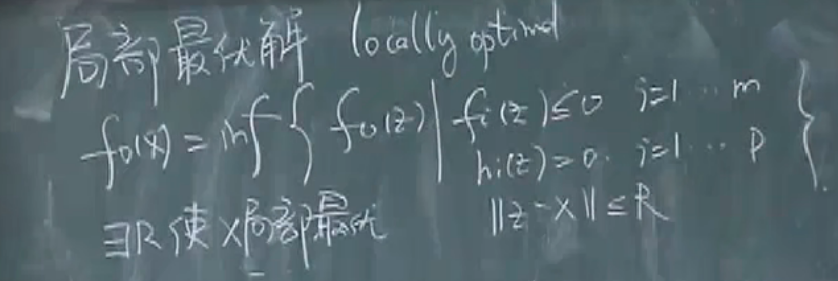
域、可行解集、全局最优解、局部最优解,ϵ\epsilonϵ解集之间的关系:
若x∈Xf,fi(x)=0x\in X_f,f_i(x)=0x∈Xf,fi(x)=0,则fi(x)≤0f_i(x)\leq 0fi(x)≤0为活动约束;fi(x)<0f_i(x)<0fi(x)<0为不活动约束。
排除临界点的方法:

可行性优化问题
可行性优化问题一般可以写成下面的形式:
find xsubject to fi(x)⩽0,i=1,⋯,mhi(x)=0,i=1,⋯,p.\begin{array}{ll} \text { find } & x \\ \text { subject to } & f_i(x) \leqslant 0, \quad i=1, \cdots, m \\ & h_i(x)=0, \quad i=1, \cdots, p . \end{array} find subject to xfi(x)⩽0,i=1,⋯,mhi(x)=0,i=1,⋯,p.
如何写成标准的形式?写成最优化一个常数。
问题的标准表示
框约束 Box Constraints
minimizef0(x)subject tol1≤xi≤ui,i=1,...,n\begin{array}{ll} \text{minimize}& f_0(x)\\ \text{subject to}& l_1\leq x_i\leq u_i,i=1,...,n \end{array} minimizesubject tof0(x)l1≤xi≤ui,i=1,...,n
即每个变量都有一个上界和下界,那么可以转换为下面的标准形式:
minimizef0(x)subject toli−xi≤0,i=1,...,nxi−ui≤0,i=1,...,n\begin{array}{ll} \text{minimize}& f_0(x)\\ \text{subject to}& l_i-x_i\leq 0,i=1,...,n\\ & x_i-u_i\leq 0,i=1,...,n \end{array} minimizesubject tof0(x)li−xi≤0,i=1,...,nxi−ui≤0,i=1,...,n
等价问题
如果从一个问题的解,很容易得到另一个问题的解,并且反之亦然,那么我们称两个问题是等价的。作为一个简单的例子,考虑:
minimizef~(x)=α0f0(x)subject to f~i(x)=αifi(x)⩽0,i=1,⋯,mh~i(x)=βihi(x)=0,i=1,⋯,p(2)\begin{array}{ll} \operatorname{minimize} & \tilde{f}(x)=\alpha_0 f_0(x) \\ \text { subject to } & \tilde{f}_i(x)=\alpha_i f_i(x) \leqslant 0, \quad i=1, \cdots, m \\ & \tilde{h}_i(x)=\beta_i h_i(x)=0, \quad i=1, \cdots, p \end{array}\tag{2} minimize subject to f~(x)=α0f0(x)f~i(x)=αifi(x)⩽0,i=1,⋯,mh~i(x)=βihi(x)=0,i=1,⋯,p(2)
很多时候约束的量级不同,量级过大导致约束的权重变化。通过等价转换,可以将问题的约束进行标准化。
目标函数和约束函数的变换
设:ψ0:R→R\psi_0:\R\rightarrow \Rψ0:R→R单增;ψ1,...,ψm:R→R\psi_1,...,\psi_m:\R\rightarrow \Rψ1,...,ψm:R→R满足:当且仅当u≤0u\leq 0u≤0时ψi(u)≤0;ψm+1,...,ψm+p:R→R\psi_i(u)\leq 0;\psi_{m+1},...,\psi_{m+p}:\R\rightarrow \Rψi(u)≤0;ψm+1,...,ψm+p:R→R满足:当且仅当u=0u=0u=0时ψi(u)=0\psi_i(u)=0ψi(u)=0。我们定义函数f~i\tilde f_if~i和h~i\tilde h_ih~i为复合函数:
f~i(x)=ψ(fi(x)),i=0,...,mh~i(x)=ψm+i(hi(x)),i=1,...,p\tilde f_i(x)=\psi(f_i(x)),i=0,...,m\qquad \tilde{h}_i(x)=\psi_{m+i}(h_i(x)),i=1,...,p f~i(x)=ψ(fi(x)),i=0,...,mh~i(x)=ψm+i(hi(x)),i=1,...,p
显然,问题
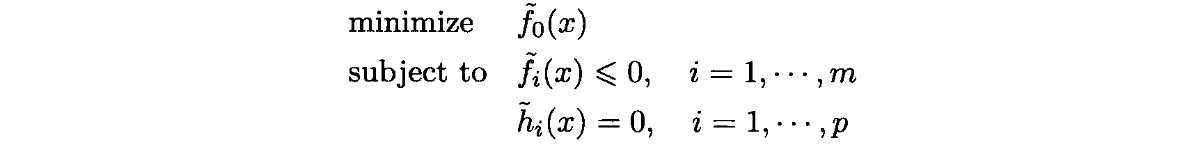
与标准形式式1等价且同解。并且式2是ψ\psiψ为线性函数的一种特例。
例:最小函数和最小范数平方问题
min∣∣AX−b∣∣2\min ||AX-b||_2 min∣∣AX−b∣∣2
上述问题是一个无约束的优化问题,等价于最小化二范数的平方。
min∣∣AX−b∣∣22\min ||AX-b||_2^2 min∣∣AX−b∣∣22
原因是原函数在实数域内单调递增。
松弛变量
fi(x)≤0f_i(x)\leq 0fi(x)≤0等价于∃si≥0,fi(x)+si(x)=0\exist s_i\geq 0,f_i(x)+s_i(x)=0∃si≥0,fi(x)+si(x)=0,将问题进行转换,得到:
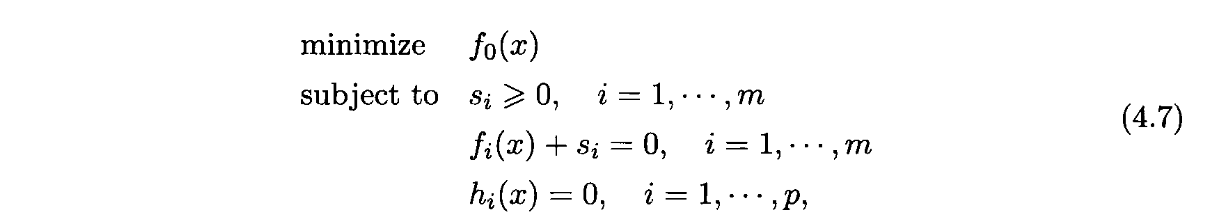
引入sis_isi后,问题就不仅是关于x的优化问题了。对于问题的凸性,需要对变量x和s同时验证。
进行松弛后,将变量的维数和约束都增加了。但有些时候,会通过松弛变量,将问题的结构转换为更加通用的结构。
等式约束的消除
例:等式约束的消除
对于优化问题而言,约束的数目越多,优化越复杂,所以消除等式约束是降低优化问题难度的一个重要方法。
{hi(x)=0,i=1,...,p}(3)\{h_i(x)=0,i=1,...,p\}\tag{3} {hi(x)=0,i=1,...,p}(3)
是一组方程。假设我们能够得到这组方程的解,那么用一组参数z∈Rkz\in \R^kz∈Rk来显式地参数化等式约束。设函数ϕ:Rk→Rn\phi:\R^k\rightarrow \R^nϕ:Rk→Rn是这样的函数:xxx满足式(3)等价于存在一些z∈Rkz\in\R^kz∈Rk,使得
x=ϕ(z)x=\phi(z) x=ϕ(z)
那么优化问题
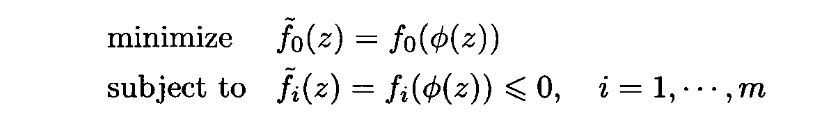
与原问题式1等价。求解出zzz后,可由x=ϕ(z)x=\phi(z)x=ϕ(z)得出最优解xxx。
相当于用变量z去表示x,然后代入原目标函数和约束中。
等式定义了一组超平面,可以表示为特解+一组基的形式。
例:消除线性等式约束AX−b=0AX-b=0AX−b=0
A∈Rp×nA\in \R^{p\times n}A∈Rp×n,是否能找到一组zzz表示X呢?
分情况讨论:
- AX−b=0AX-b=0AX−b=0无解,那么原问题无可行解
- 反之,令x0x_0x0为等式约束的任意可行解,那么通解可以表示为Fz+x0Fz+x_0Fz+x0。即ϕ(z)=Fz+x0\phi (z)=Fz+x_0ϕ(z)=Fz+x0
二、凸优化
标准形式的凸优化问题
凸优化问题是形如:
minimizef0(x)subject to fi(x)⩽0,i=1,⋯,maix=bi,i=1,⋯,p(4)\begin{array}{ll} \operatorname{minimize} & f_0(x) \\ \text { subject to } & f_i(x) \leqslant 0, \quad i=1, \cdots, m \\ & a_i^x=b_i, \quad i=1, \cdots, p \end{array}\tag{4} minimize subject to f0(x)fi(x)⩽0,i=1,⋯,maix=bi,i=1,⋯,p(4)
从广义上来说,如果目标函数是一个凸函数,约束的集合为凸集,那么问题就是凸问题。
狭义上的凸问题:
- 目标函数是凸函数
- 不等式约束的函数也是凸函数
- 等式约束函数是仿射函数
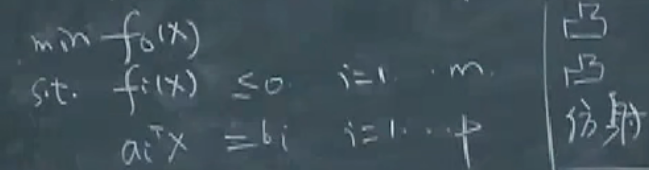
在这样的定义下,凸优化问题的可行域一定是凸的,因为他是问题定义域
D=⋂i=0mdomfi\mathcal{D}=\bigcap_{i=0}^m\bold{dom}f_i D=i=0⋂mdomfi
(凸集),m个下水平集,以及p个超平面的交集。因此,在凸优化问题中,我们是在一个凸集上极小化一个凸的函数。
若目标函数变为拟凸函数,那么该问题成为拟凸优化问题。但如果目标函数是凹函数,或者其他函数,那么我们统一称之为非凸优化问题。
例:
minf0(x)=x12+x22s.t.{f1(x):x11+x22≤0h1(x):(x1+x2)2=0\min f_0(x)=x_1^2+x_2^2\\ \text{s.t.}\begin{cases}f_1(x):\frac{x_1}{1+x_2^2}\leq 0\\ h_1(x):(x_1+x_2)^2=0\end{cases} minf0(x)=x12+x22s.t.{f1(x):1+x22x1≤0h1(x):(x1+x2)2=0
表面上看不是狭义的凸问题,可以转换为下面的形式:
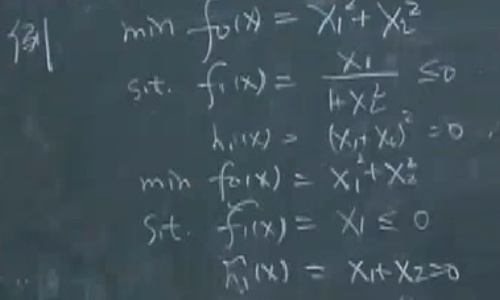
如果等式约束是一个放射约束,那么可利用等式约束对问题进行降维:
一般来说,不对问题进行降维,有必要的情况才会进行降维。
凹最大化问题
约束不变,若目标是最大化一个凹函数,那么等价于最小化一个凸函数,即,该情况下仍是凸优化问题。
maxf0(x)⇔min−f0(x)\max f_0(x)\Leftrightarrow \min -f_0(x) maxf0(x)⇔min−f0(x)
同理,如果f0(x)f_0(x)f0(x)是拟凹的,那么最大化该问题被称为拟凹的。
局部最优解与全局最优解
对于凸问题来说,局部最优解一定是全局最优解。
局部最优:∃R>0,f0(x)=inf{f0(z)∣z可行,x可行,∣∣x−z∣∣≤R}\exist R>0,f_0(x)=\inf \{f_0(z)|z可行,x可行,||x-z||\leq R\}∃R>0,f0(x)=inf{f0(z)∣z可行,x可行,∣∣x−z∣∣≤R}
证明:
设xxx不是全局最优解,即∃y\exists y∃y可行,f0(y)<f0(x)f_0(y)< f_0(x)f0(y)<f0(x)。
又因为xxx是局部最优的,那么∣∣y−x∣∣2>R||y-x||_2> R∣∣y−x∣∣2>R,那么可以构造出一个新的解:z=(1−θ)x+θy,θ=R2∣∣y−x∣∣2∈[0,12]z=(1-\theta)x+\theta y,\theta=\frac{R}{2||y-x||_2}\in[0,\frac{1}{2}]z=(1−θ)x+θy,θ=2∣∣y−x∣∣2R∈[0,21],所以z是x和y的凸组合。又因为可行解集一定是个凸集,所以z一定在可行解集内,即zzz可行。
又因为f0(x)f_0(x)f0(x)是凸函数,故
f0(z)≤θf0(x)+(1−θ)f0(y)∣∣z−x∣∣2=θ∣∣x−y∣∣2=R2(2.2)f_0(z)\leq \theta f_0(x)+(1-\theta)f_0(y)\\ ||z-x||_2=\theta ||x-y||_2=\frac{R}{2}\tag{2.2} f0(z)≤θf0(x)+(1−θ)f0(y)∣∣z−x∣∣2=θ∣∣x−y∣∣2=2R(2.2)
即zzz在x的邻域内。因为x是局部最优解,故f0(x)<f0(z)f_0(x)<f_0(z)f0(x)<f0(z)。
即,综上所述,需要满足下面的条件:
f0(y)<f0(x)f0(x)<f0(z)f_0(y)<f_0(x)\\ f_0(x)<f_0(z) f0(y)<f0(x)f0(x)<f0(z)
即f
f0(y)<f0(x)<f0(z)f_0(y)<f_0(x)<f_0(z) f0(y)<f0(x)<f0(z)
与式2.2矛盾。故x一定是全局最优解。
图形表示:
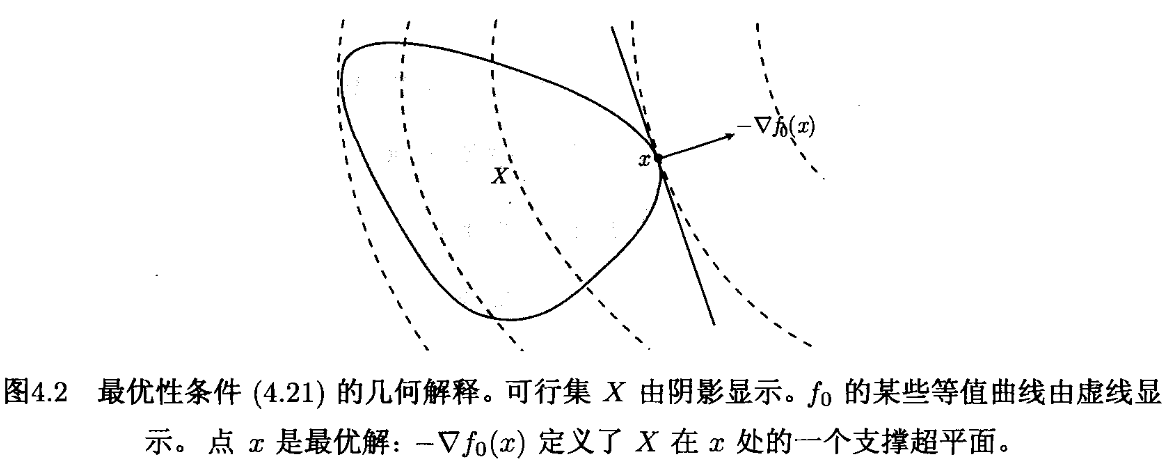
可微函数f0f_0f0的最优性准则
可微凸问题目标函数的一阶条件:
f0(y)≥f0(x)+∇f0T(x)⋅(y−x)∀x,y∈domff_0(y)\geq f_0(x)+\nabla f_0^T(x)\cdot (y-x)\qquad \forall x,y\in \bold{dom}f f0(y)≥f0(x)+∇f0T(x)⋅(y−x)∀x,y∈domf
问题的可行域:
Xf={x∣fi(x)≤0,i=1,...,m;hi(x)=0,i=1,...,p}X_f=\{x|f_i(x)\leq 0,i=1,...,m;h_i(x)=0,i=1,...,p\} Xf={x∣fi(x)≤0,i=1,...,m;hi(x)=0,i=1,...,p}
那么X∗∈XfX^*\in X_fX∗∈Xf最优等价于
∇f0T(X∗)(y−X∗)≥0(2.3)\nabla f_0^T(X^*)(y-X^*)\geq 0\tag{2.3} ∇f0T(X∗)(y−X∗)≥0(2.3)
约束仅为等式约束
minf0(x)domf0=Rns.t.AX=b\min f_0(x)\\ \bold{dom}f_0=\R^n\\ s.t. AX=b minf0(x)domf0=Rns.t.AX=b
若∃x,AX=b\exist x,AX=b∃x,AX=b,那么X最优等价于∀y,Ay=b,∇f0T(x)(y−x)≥0\forall y,Ay=b,\nabla f_0^T(x)(y-x)\geq 0∀y,Ay=b,∇f0T(x)(y−x)≥0成立。
又因为AX=b,Ay=bAX=b,Ay=bAX=b,Ay=b,那么y=X+v,v∈N(A)y=X+v,v\in \mathcal{N}(A)y=X+v,v∈N(A),即A的化零空间中的一个向量。
y是方程组的解,等于通解v加上特解X
因此,最优性条件可表示为
∇f0(x)v≥0,∀v∈N(A)\nabla f_0(x)v\geq 0,\forall v\in \mathcal N(A) ∇f0(x)v≥0,∀v∈N(A)
那么只有两种情况:
-
子空间退化为零点:那么y==Xy==Xy==X,即方程只有一个解,矩阵A是可逆的。
-
∇f0(x)\nabla f_0(x)∇f0(x)正交于子空间:
约束仅为非负约束:互补条件
minf0(x)s.t.x≥0\min f_0(x)\\ s.t.x\geq 0 minf0(x)s.t.x≥0
若∃x≥0\exist x\geq 0∃x≥0,xxx最优等价于∀y≥0\forall y\geq 0∀y≥0
∇f0T(x)(y−x)≥0即∇f0T(x)y−∇f0T(x)x≥0\nabla f_0^T(x)(y-x)\geq 0\\ 即\nabla f_0^T(x)y-\nabla f_0^T(x)x\geq 0 ∇f0T(x)(y−x)≥0即∇f0T(x)y−∇f0T(x)x≥0
- ①:若∇f0T(x)≤0\nabla f_0^T(x)\leq 0∇f0T(x)≤0,则∇f0T(x)y\nabla f_0^T(x)y∇f0T(x)y必可以取无穷小,则必有∇f0(x)≥0\nabla f_0(x)\geq 0∇f0(x)≥0
- ② ∀y\forall y∀y均有∇f0(x)T(y−x)≥0\nabla f_0(x)^T(y-x)\geq 0∇f0(x)T(y−x)≥0,当y=0时,∇f0T(x)x≤0\nabla f_0^T(x)x\leq 0∇f0T(x)x≤0
- ③ ∇f0T(x)≥0,x≥0,\nabla f_0^T(x)\geq 0,x\geq 0,∇f0T(x)≥0,x≥0,则∇f0T(x)x≥0\nabla f_0^T(x)x\geq 0∇f0T(x)x≥0
由②和③可知,f0T(x)x=0f_0^T(x)x=0f0T(x)x=0
结论:如果x是最优解,那么一定满足下面的条件
{x≥0∇f0(x)≥0(∇f0(x))ixi=0\begin{cases}x\geq 0\\ \nabla f_0(x)\geq 0\\ (\nabla f_0(x))_ix_i=0\end{cases} ⎩⎨⎧x≥0∇f0(x)≥0(∇f0(x))ixi=0
该条件称为互补条件。
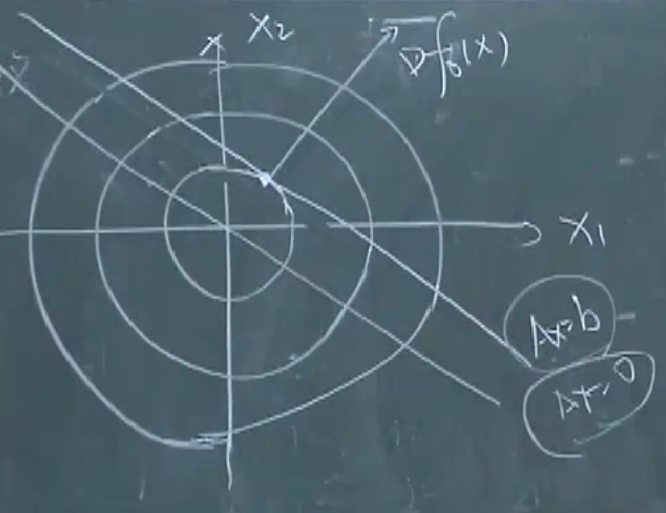
几何解释:

相关文章:

凸优化学习:PART3凸优化问题(持续更新)
凸优化问题 凸优化问题的广义定义: 目标函数为凸函数约束集合为凸集 一、优化问题 基本用语 一般优化问题的描述: minimizef0(x)subject to fi(x)⩽0,i1,⋯,mhi(x)0,i1,⋯,p(1)\begin{array}{ll} \operatorname{minimize} & f_0(x) \\ \text { s…...
)
[ue4] 着色器绑定(Shader Binding)
当我们在ue4中制作了一个美术材质之后,引擎本身会为我们做很多事情,它会把结点翻译为hlsl,生成多个shader变体,并在多个mesh pass中去选择性的调用所需的shader,其中一个重要的过程就是获取shader绑定的数据。 本文将主…...

Rust语言之迭代器
文章目录Rust迭代器Rust迭代器的实现Iterator特型IntoIterator特型for循环与迭代器迭代器类型再看for循环实现自定义迭代器方式一方式二相关参考Rust迭代器 Rust语言内置了迭代器模式,用于实现对一个项的序列进行特定的处理,通常配合for循环使用。当我们…...
TreeSet 与 TreeMap And HashSet 与 HashMap
目录 Map TreeMap put()方法 : get()方法 : Set> entrySet() (重) : foreach遍历 : Set 哈希表 哈希冲突 : 冲突避免 : 冲突解决 ---- > 比散列(开放地址法) : 开散列 (链地址法 . 开链法) 简介 : 在Java中 , TreeSet 与 TreeMap 利用搜索树实现 Ma…...
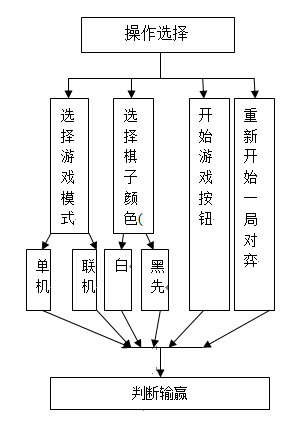
Java围棋游戏的设计与实现
技术:Java等摘要:围棋作为一个棋类竞技运动,在民间十分流行,为了熟悉五子棋规则及技巧,以及研究简单的人工智能,决定用Java开发五子棋游戏。主要完成了人机对战和玩家之间联网对战2个功能。网络连接部分为S…...

第七十三章 使用 irisstat 实用程序监控 IRIS - 使用选项运行 irisstat
文章目录第七十三章 使用 irisstat 实用程序监控 IRIS - 使用选项运行 irisstat使用选项运行 irisstatirisstat Options第七十三章 使用 irisstat 实用程序监控 IRIS - 使用选项运行 irisstat 使用选项运行 irisstat 不带选项运行 irisstat 会生成基本报告。通常,…...

【博客619】PromQL如何实现Left joins以及不同metrics之间的复杂联合查询
PromQL如何实现Left joins以及不同metrics之间的复杂联合查询 1、场景 我们需要在PromQL中实现类似SQL中的连接查询: SELECT a.value*b.value, * FROM a, b2、不同metrics之间的复杂联合查询 瞬时向量与瞬时向量之间进行数学运算: 例如:根…...
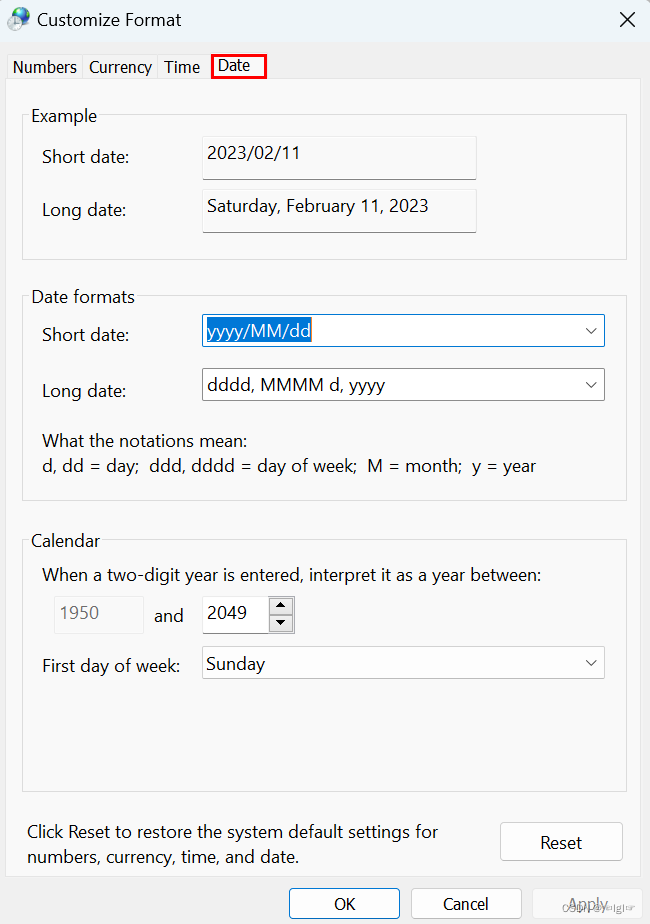
Win11自定义电脑右下角时间显示格式
Win11自定义电脑右下角时间显示格式 一、进入附加设置菜单 1、进入控制面板,选择日期和时间 2、选择修改日期和时间 3、选择修改日历设置 4、选择附加设置 二、自定义时间显示出秒 1、在选项卡中,选时间选项卡 2、在Short time的输入框中输入H:m…...
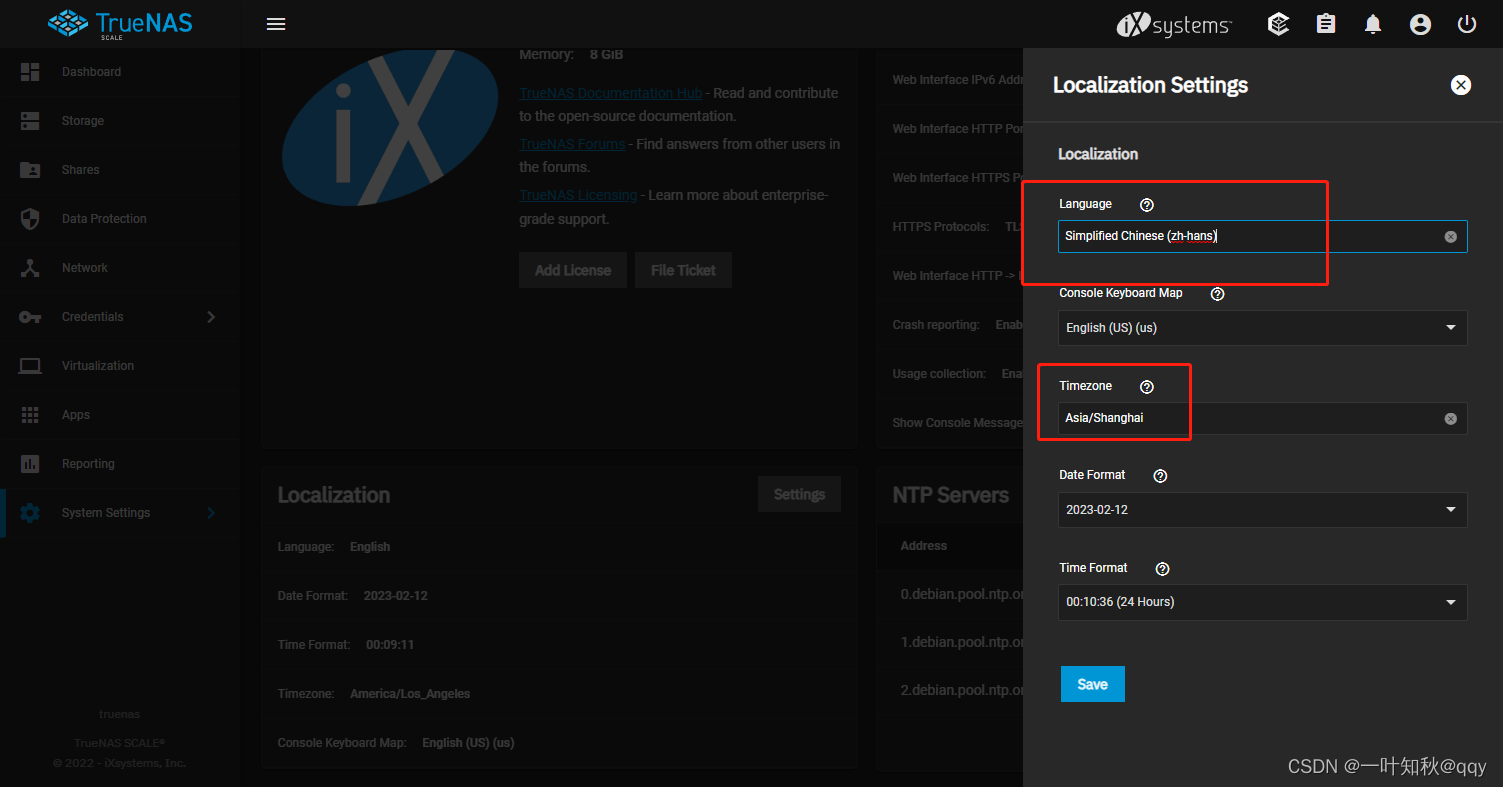
TrueNas篇-trueNas Scale安装
安装TrueNAS Scale 在尝试trueNas core时发下可以成功安装,但是一直无法成功启动,而且国内对我遇见的错误几乎没有案例,所以舍弃掉了,而且trueNas core是基于Linux的,对Linux的生态好了很多,还可以可以在t…...
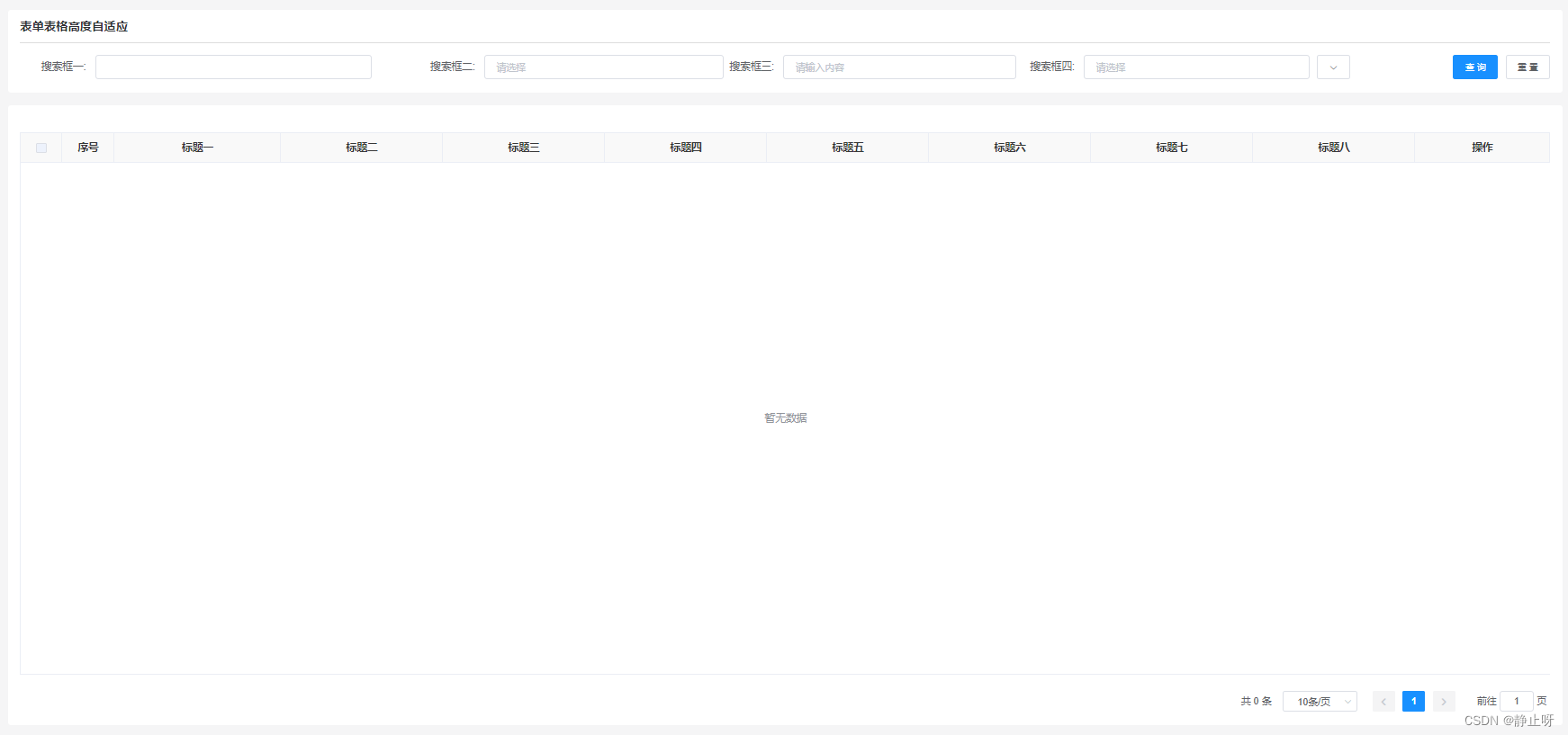
element表单搜索框与表格高度自适应
一般在后台管理系统中,表单搜索框和表格的搭配是非常常见的,如下所示: 在该图中,搜索框有五个,分为了两行排列。但根据大多数的UI标准,搜索框默认只显示一行,多余的需要进行隐藏。此时的页面被…...

MySQL使用技巧整理
title: MySQL使用技巧整理 date: 2021-04-11 00:00:00 tags: MySQL categories:数据库 重建索引 索引可能因为删除,或者页分裂等原因,导致数据页有空洞,重建索引的过程会创建一个新的索引,把数据按顺序插入,这样页面…...

七大设计原则之里氏替换原则应用
目录1 里氏替换原则2 里氏替换原则应用1 里氏替换原则 里氏替换原则(Liskov Substitution Principle,LSP)是指如果对每一个类型为 T1 的对象 o1,都有类型为 T2 的对象 o2,使得以 T1 定义的所有程序 P 在所有的对象 o1 都替换成 o2 时,程序 P…...

1行Python代码去除图片水印,网友:一干二净
大家好,这里是程序员晚枫。 最近小明在开淘宝店(店名:爱吃火锅的少女),需要给自己的原创图片加水印,于是我上次给她开发了增加水印的功能:图片加水印,保护原创图片,一行…...
)
Connext DDS属性配置参考大全(2)
DDSSecure安全com.rti.servcom.rti.serv.load_plugin...
)
一起Talk Android吧(第四百九十二回:精简版动画)
文章目录概念介绍使用方法示例代码经验总结各位看官们大家好,上一回中咱们说的例子是"动画集合:AnimatorSetBuilder",这一回中咱们说的例子是" 精简版动画"。闲话休提,言归正转,让我们一起Talk Android吧&…...
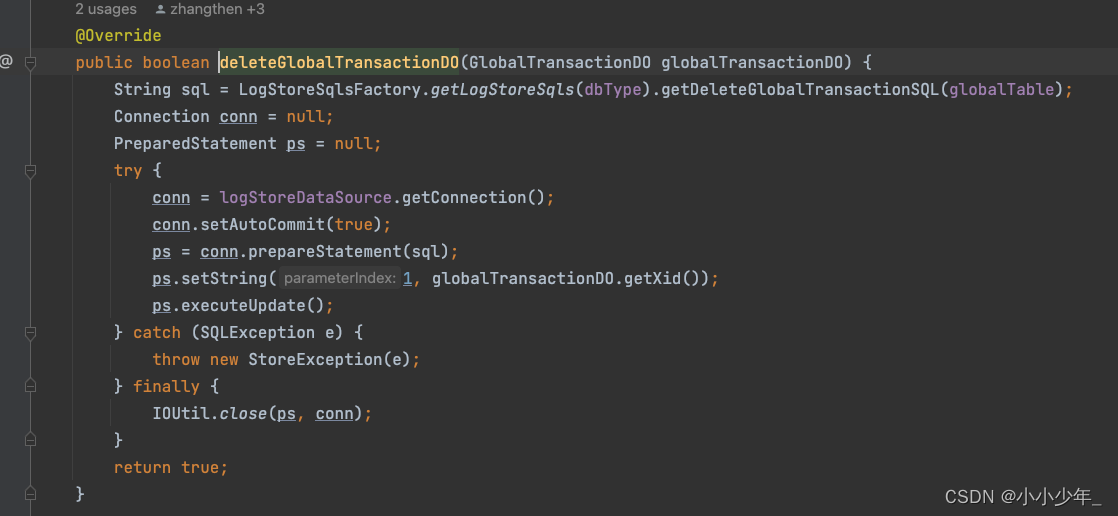
seata源码-全局事务回滚服务端源码
这篇博客来记录在发起全局事务回滚时,服务端接收到netty请求是如何处理的 1. 发起全局事务回滚请求 在前面的博客中,有说到过,事务发起者在发现分支事务执行异常之后,会提交全局事务回滚的请求到netty服务端,这里是发…...
【Vue3源码】第一章 effect和reactive
文章目录【Vue3源码】第一章 effect和reactive前言1、实现effect函数2、封装track函数(依赖收集)3、封装reactive函数4、封装trigger函数(依赖触发)5、单元测试【Vue3源码】第一章 effect和reactive 前言 今天就正式开始Vue3源码…...

C函数指针
函数指针是指向函数的指针变量。通常我们说的指针变量是指向一个整型、数组或字符型等变量,而函数指针是指向函数。函数指针可以像一般函数一样,用于调用函数、传递参数。函数指针变量的声明:typedef int (*fun_ptr)(int,int); // 声明一个指…...

2023同等学力申请硕士计算机综合国考
同等学力国考报名要开始了 2023年2月15日,中国教育考试网和“全国同等学力人员申请硕士学位管理工作信息平台”(https://tdxl.chsi.com.cn,联系服务电话:010-67410388)公布报名工作通知。考生须按照通知要求进行注册或…...

英语基础-并列句概述
什么是并列句?并列句就是用连词把独立的句子连接起来,使得句子之间产生并列的逻辑。 1. 并列句中的逻辑 1. 小明步行上学,小红骑自行车上班。 Ming goes to school on foot,and Hong goes to work by bike. 平行逻辑 2. 小红经常玩手机…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

Python环境安装与虚拟环境配置详解
本文档旨在为Python开发者提供一站式的环境安装与虚拟环境配置指南,适用于Windows、macOS和Linux系统。无论你是初学者还是有经验的开发者,都能在此找到适合自己的环境搭建方法和常见问题的解决方案。 快速开始 一分钟快速安装与虚拟环境配置 # macOS/…...

break 语句和 continue 语句
break语句和continue语句都具有跳转作用,可以让代码不按既有的顺序执行 break break语句用于跳出代码块或循环 1 2 3 4 5 6 for (var i 0; i < 5; i) { if (i 3){ break; } console.log(i); } continue continue语句用于立即终…...
