七大设计原则之里氏替换原则应用
目录
- 1 里氏替换原则
- 2 里氏替换原则应用
1 里氏替换原则
里氏替换原则(Liskov Substitution Principle,LSP)是指如果对每一个类型为 T1 的对象 o1,都有类型为 T2 的对象 o2,使得以 T1 定义的所有程序 P 在所有的对象 o1 都替换成 o2 时,程序 P 的行为没有发生变化,那么类型 T2 是类型 T1 的子类型。
定义看上去还是比较抽象,我们重新理解一下,可以理解为一个软件实体如果适用一个父类的话,那一定是适用于其子类,所有引用父类的地方必须能透明地使用其子类的对象,子类对象能够替换父类对象,而程序逻辑不变。根据这个理解,我们总结一下:
引申含义:子类可以扩展父类的功能,但不能改变父类原有的功能。
1、子类可以实现父类的抽象方法,但不能覆盖父类的非抽象方法。
2、子类中可以增加自己特有的方法。
3、当子类的方法重载父类的方法时,方法的前置条件(即方法的输入/入参)要比父类方法的输入参数更宽松。
4、当子类的方法实现父类的方法时(重写/重载或实现抽象方法),方法的后置条件(即方法的输出/返回值)要比父类更严格或相等。
在前面讲开闭原则的时候埋下了一个伏笔,我们记得在获取折后时重写覆盖了父类的 getPrice()方法,增加了一个获取源码的方法 getOriginPrice(),显然就违背了里氏替换原则。我们修改一下代码,不应该覆盖 getPrice()方法,增加 getDiscountPrice()方法:
之前:
public class JavaDiscountCourse extends JavaCourse {public JavaDiscountCourse(Integer id, String name, Double price) {super(id, name, price);}public Double getOriginPrice(){return super.getPrice();}public Double getPrice(){return super.getPrice() * 0.61;}}更正:
public class JavaDiscountCourse extends JavaCourse {public JavaDiscountCourse(Integer id, String name, Double price) {super(id, name, price);}public Double getDiscountPrice(){return super.getPrice() * 0.61;}
}
2 里氏替换原则应用
使用里氏替换原则有以下优点:
1、约束继承泛滥,开闭原则的一种体现。
2、加强程序的健壮性,同时变更时也可以做到非常好的兼容性,提高程序的维护性、扩展性。降低需求变更时引入的风险。现在来描述一个经典的业务场景,用正方形、矩形和四边形的关系说明里氏替换原则,我们都知道正方形是一个特殊的长方形,那么就可以创建一个长方形父类 Rectangle 类:
public class Rectangle {private long height;private long width;public long getHeight() {return height;}public void setHeight(long height) {this.height = height;}public long getWidth() {return width;}public void setWidth(long width) {this.width = width;}
}
创建正方形 Square 类继承长方形:
public class Square extends Rectangle {private long length;public long getLength() {return length;}public void setLength(long length) {this.length = length;}@Overridepublic long getHeight() {return getLength();}@Overridepublic void setHeight(long height) {setLength(height);}@Overridepublic long getWidth() {return getLength();}@Overridepublic void setWidth(long width) {setLength(width);}
}
在测试类中创建 resize()方法,根据逻辑长方形的宽应该大于等于高,我们让高一直自增,知道高等于宽变成正方形:
public static void resize(Rectangle rectangle){while (rectangle.getWidth() >= rectangle.getHeight()){rectangle.setHeight(rectangle.getHeight() + 1);System.out.println("Width:" +rectangle.getWidth() +",Height:" + rectangle.getHeight());}System.out.println("Resize End,Width:" +rectangle.getWidth() +",Height:" + rectangle.getHeight());
}
测试代码:
public static void main(String[] args) {
Rectangle rectangle = new Rectangle();
rectangle.setWidth(20);
rectangle.setHeight(10);
resize(rectangle);
}
运行结果:

发现高比宽还大了,在长方形中是一种非常正常的情况。现在我们再来看下面的代码,把长方形Rectangle 替换成它的子类正方形 Square,修改测试代码:
public static void main(String[] args) {Square square = new Square();square.setLength(10);resize(square);
}
这时候我们运行的时候就出现了死循环,违背了里氏替换原则,将父类替换为子类后,程序运行结果没有达到预期。因此,我们的代码设计是存在一定风险的。里氏替换原则只存在父类与子类之间,约束继承泛滥。我们再来创建一个基于长方形与正方形共同的抽象四边形 Quadrangle 接口:
public interface QuadRangle {long getWidth();long getHeight();
}
修改长方形 Rectangle 类:
public class Rectangle implements QuadRangle {
private long height;
private long width;public long getHeight() {return height;}public void setHeight(long height) {this.height = height;}public long getWidth() {return width;}public void setWidth(long width) {this.width = width;}
}
修改正方形类 Square 类:
public class Square implements QuadRangle {private long length;public long getLength() {return length;}public void setLength(long length) {this.length = length;}public long getWidth() {return length;}public long getHeight() {return length;}
}
此时,如果我们把 resize()方法的参数换成四边形 Quadrangle 类,方法内部就会报错。因为正方形 Square 已经没有了 setWidth()和 setHeight()方法了。因此,为了约束继承泛滥,resize()的方法参数只能用 Rectangle 长方形。当然,我们在后面的设计模式中还会继续深入讲解。
相关文章:

七大设计原则之里氏替换原则应用
目录1 里氏替换原则2 里氏替换原则应用1 里氏替换原则 里氏替换原则(Liskov Substitution Principle,LSP)是指如果对每一个类型为 T1 的对象 o1,都有类型为 T2 的对象 o2,使得以 T1 定义的所有程序 P 在所有的对象 o1 都替换成 o2 时,程序 P…...

1行Python代码去除图片水印,网友:一干二净
大家好,这里是程序员晚枫。 最近小明在开淘宝店(店名:爱吃火锅的少女),需要给自己的原创图片加水印,于是我上次给她开发了增加水印的功能:图片加水印,保护原创图片,一行…...
)
Connext DDS属性配置参考大全(2)
DDSSecure安全com.rti.servcom.rti.serv.load_plugin...
)
一起Talk Android吧(第四百九十二回:精简版动画)
文章目录概念介绍使用方法示例代码经验总结各位看官们大家好,上一回中咱们说的例子是"动画集合:AnimatorSetBuilder",这一回中咱们说的例子是" 精简版动画"。闲话休提,言归正转,让我们一起Talk Android吧&…...
seata源码-全局事务回滚服务端源码
这篇博客来记录在发起全局事务回滚时,服务端接收到netty请求是如何处理的 1. 发起全局事务回滚请求 在前面的博客中,有说到过,事务发起者在发现分支事务执行异常之后,会提交全局事务回滚的请求到netty服务端,这里是发…...
【Vue3源码】第一章 effect和reactive
文章目录【Vue3源码】第一章 effect和reactive前言1、实现effect函数2、封装track函数(依赖收集)3、封装reactive函数4、封装trigger函数(依赖触发)5、单元测试【Vue3源码】第一章 effect和reactive 前言 今天就正式开始Vue3源码…...

C函数指针
函数指针是指向函数的指针变量。通常我们说的指针变量是指向一个整型、数组或字符型等变量,而函数指针是指向函数。函数指针可以像一般函数一样,用于调用函数、传递参数。函数指针变量的声明:typedef int (*fun_ptr)(int,int); // 声明一个指…...

2023同等学力申请硕士计算机综合国考
同等学力国考报名要开始了 2023年2月15日,中国教育考试网和“全国同等学力人员申请硕士学位管理工作信息平台”(https://tdxl.chsi.com.cn,联系服务电话:010-67410388)公布报名工作通知。考生须按照通知要求进行注册或…...

英语基础-并列句概述
什么是并列句?并列句就是用连词把独立的句子连接起来,使得句子之间产生并列的逻辑。 1. 并列句中的逻辑 1. 小明步行上学,小红骑自行车上班。 Ming goes to school on foot,and Hong goes to work by bike. 平行逻辑 2. 小红经常玩手机…...
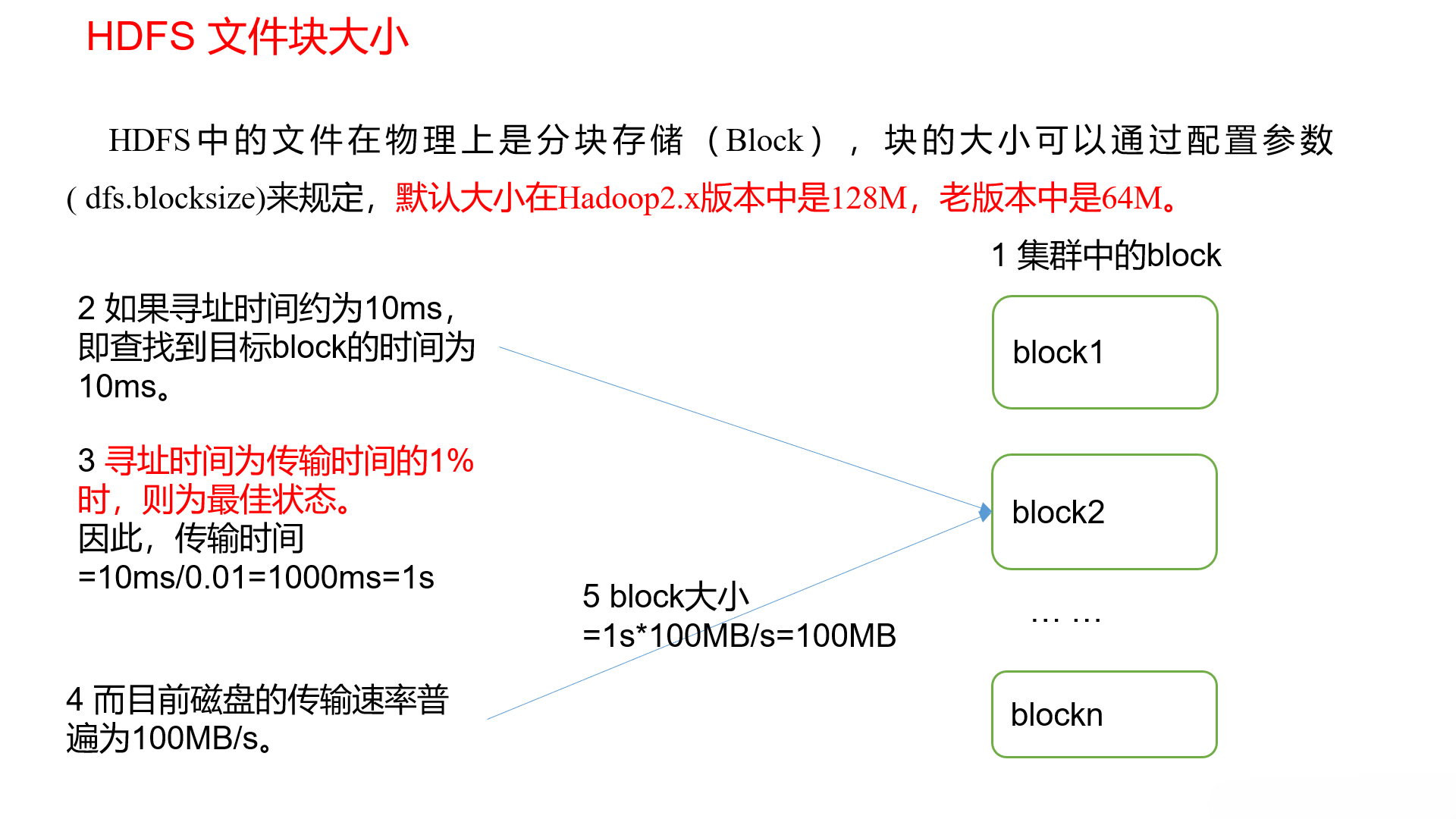
大数据框架之Hadoop:HDFS(一)HDFS概述
1.1HDFS产出背景及定义 HDFS 产生背景 随着数据量越来越大,在一个操作系统存不下所有的数据,那么就分配到更多的操作系统管理的磁盘中,但是不方便管理和维护,迫切需要一种系统来管理多台机器上的文件,这就是分布式文件…...
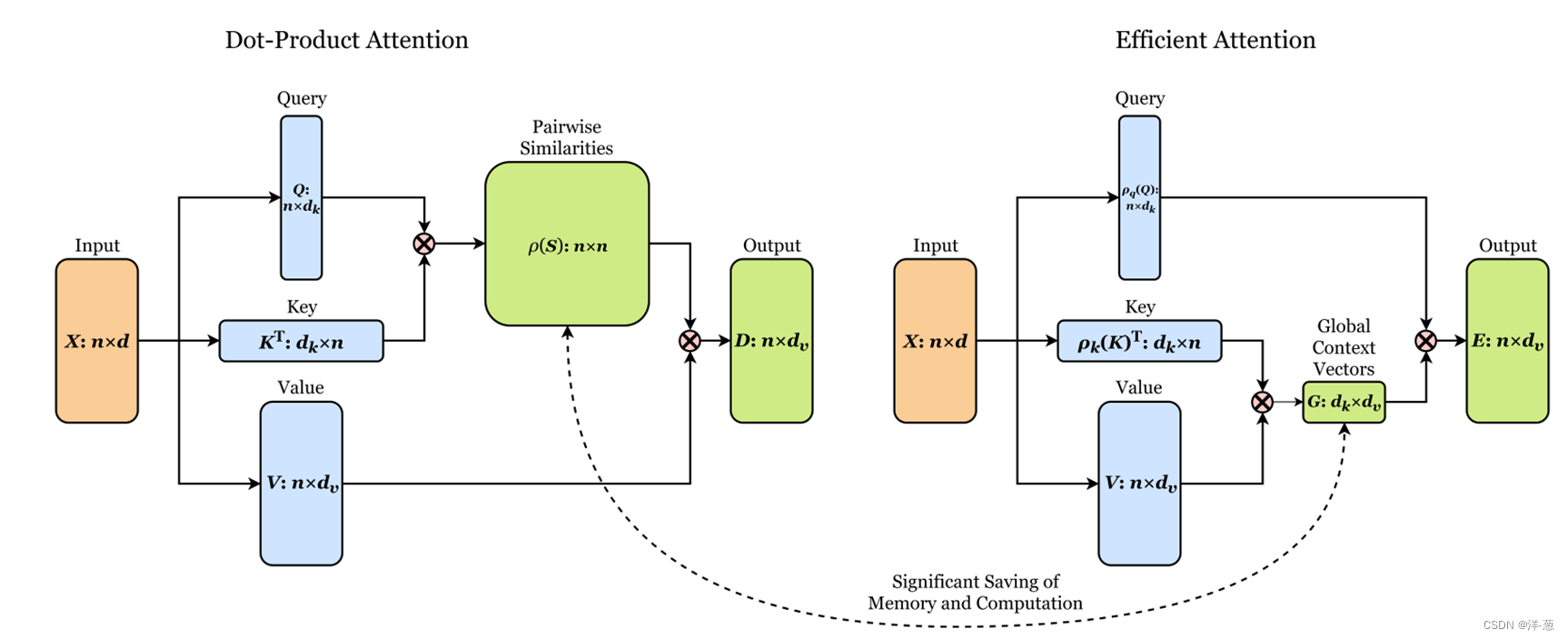
20230210组会论文总结
目录 【Ultra-High-Definition Low-Light Image Enhancement: A Benchmark and Transformer-Based Method】 【ShuffleMixer: An Efficient ConvNet for Image Super-Resolution】 【A Close Look at Spatial Modeling: From Attention to Convolution 】 【DEA-Net: Single i…...

Python - 数据容器dict(字典)
目录 字典的定义 字典数据的获取 字典的嵌套 字典的各种操作 新增与更新元素 [Key] Value 删除元素 pop和del 清空字典 clear 获取全部的键 keys 遍历字典 容器通用功能总览 字典的定义 使用{},不过存储的元素是一个个的:键值对&#…...
)
傻白探索Chiplet,文献阅读笔记汇总(十二)
Summary(方便分类管理) Article(文献出处) 方便再次搜索 Data(文献数据) 总结归纳,方便理解 Comments(对文献的想法)/Why(为什么看这篇文献)强…...

#电子电气架构——Vector工具常见问题解决三板斧
我是穿拖鞋的汉子,魔都中一位坚持长期主义的工科男。 今天在与母亲聊天时,得到老家隔壁邻居一位大姐年初去世的消息,挺让自己感到伤感!岁月如流水,想抓都抓不住。想起平时自己加班的那个程度,可能后续也要自己注意身体啦。 老规矩,分享一段喜欢的文字,避免自己成为高知…...

文本三剑客之grep
Grep是Linux用户用来搜索文本字符串的命令行工具。您可以使用它在文件中搜索某个单词或单词的组合,也可以将其他Linux命令的输出通过管道传输到grep,因此grep可以仅显示您需要查看的输出。grep的命令格式如下:grep 选项 查找条件 目标文件…...
pwn手记录题1
fuzzerinstrospector(首届数字空间安全攻防大赛) 主体流程(相对比较简单,GLibc为常见的2.27版本, Allocate申请函数(其中有两个输入函数Read_8Int、Read_context; 还存在着后门函数; 关键点在于如何利用…...

自动驾驶规划 - Apollo Lattice Planner算法【1】
文章目录Lattice Planner简介Lattice Planner 算法思路1. 离散化参考线的点2. 在参考线上计算匹配点3. 根据匹配点,计算Frenet坐标系的S-L值4. parse the decision and get the planning target5. 生成横纵向采样路径6. 轨迹cost值计算,进行碰撞检测7. 优…...
以太坊数据开发-Web3.py-安装连接以太坊数据
Web3.py是连接以太坊的python库,它的API从web3.js中派生而来。如果你用过web3.js,你会对它的API很熟悉。但惭愧的是,作为一个以太坊上Dapp的开发者,我几乎没有直接使用过web3.js,也没有看过它的API。 官网:…...
【触摸屏功能测试】MQTT_STD本地调试说明-测试记录
1、MQTT简介 MQTT是一种基于发布/订阅模式的“轻量级”通讯协议。它是针对受限的、低带宽的、高延迟的、网络不可靠的环境下的网络通讯设备设计的。 发布是指客户端将消息传递给服务器,订阅是指客户端接收服务器推送的消息。每个消息有一个主题,包含若干…...

六十分之十三——黎明前
目录一、目标二、计划三、完成情况四、提升改进(最少3点)五、意外之喜(最少2点)六、总结一、目标 明确可落地,对于自身执行完成需要一定的努力才可以完成的 1.8本技术管理书籍阅读(使用番茄、快速阅读、最后输出思维导图)2.吴军系列硅谷来信1听书、香帅的北大金融…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
