蓝桥杯冲击-02约数篇(必考)
文章目录
前言
一、约数是什么
二、三大模板
1、试除法求约数个数
2、求约数个数
3、求约数之和
三、真题演练
前言
约数和质数一样在蓝桥杯考试中是在数论中考察频率较高的一种,在省赛考察的时候往往就是模板题,难度大一点会结合其他知识点考察,但是仍然会用到模板,这里有三大模板,第一个是试除法求约数个数,第二个是求约数个数,第三个是求约数的和(来自y总的三个模型)
一、约数是什么
约数(约数的含义是什么) 1、意思 1.大约的数目。 2.一个数能够整除另一数,这个数就是另一数的约数。如2,3,4,6都能整除12,因此2,3,4,6都是12的约数。也叫因数。最后俩个都插到这个动态数组中,但是注意
二、三大模板
1、试除法求约数个数
算法思想:算x的约数,对 小于等于x的根号数求约数,当你求得一个约数,对应的也有另一个数是约数,就比如算12的约数,当算出3是约数,可得 4(12/ 3)也是12的约数。但是注意如果16的约数4对应的约数还是4不能在被放进去,所以要加一个特判
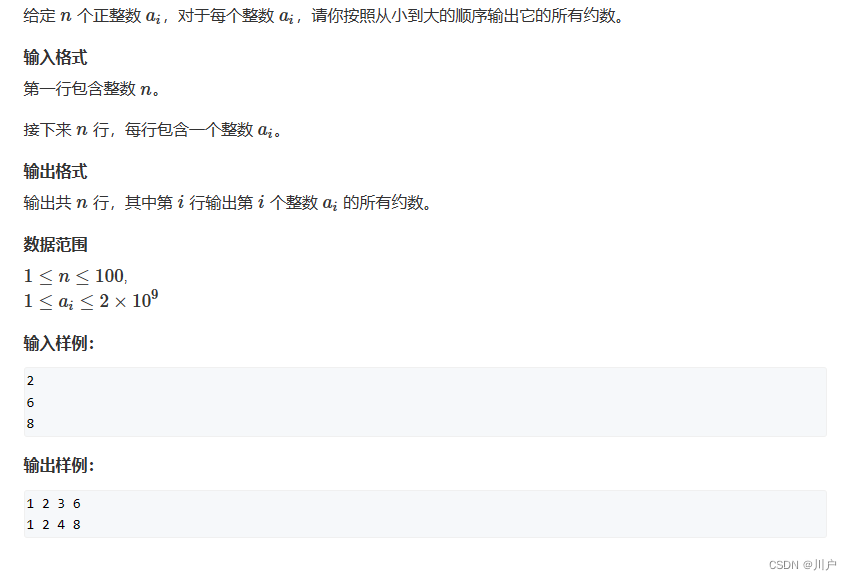
代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>using namespace std;vector<int> get_divisors(int n)
{vector <int> res;for(int i = 1;i <= n / i; i ++){if(n % i == 0){res.push_back(i);if(i != n / i) res.push_back(n/i);}}sort(res.begin(),res.end());return res;
}
int main()
{int n;cin >> n;while(n --){int x;cin >> x;vector <int> res;res = get_divisors(x);for(auto c : res){cout << c << " ";}cout << endl;}
}2、求约数个数
如果有一个数n,且 n = p1^c1 * p2 ^ c2 * p3 ^c3 + ...... + pn^cn;
那么它的约数个数和就等于 (c1 + 1 ) * ( c2 + 1 ) * (c3 + 1 ) ....(cn + 1);
p1^c1,这样的数就是上文中所介绍的质因数,通过求质因数,在求c1 + 1的值即可。
题目·

代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
const int mod = 1e9 + 7;
typedef long long LL;
using namespace std;
int main()
{unordered_map <int,int> primes;int n;cin >> n;while (n -- ){int x;cin >> x;for(int i = 2;i <= x / i;i ++){while(x % i == 0){x /= i;primes[i] ++;}}if(x > 1) primes[x] ++;}LL res = 1;for(auto c: primes){res = res * (c.second + 1) % mod;}cout << res << endl;
}3、求约数之和
如果有一个数n,且 n = p1^c1 * p2 ^ c2 * p3 ^c3 + ...... + pn^cn;
那么它的约数之和为(p1^0 + p2^1 + p3 ^3 + .. +p^c1) * ... *( pn^c1 + pn^c2 +pn^c3 + ...+ pn^cn)
求解方法和上面一样,先是解出质因数,然后求出约数和的过程很巧妙,看下面代码
题目

题解
#include <bits/stdc++.h>
typedef long long LL;
const int mod = 1e9 + 7;
using namespace std;
int main()
{unordered_map<int,int> primes; //一个值存的是这个质因数,第二个存的是指数int n;cin >>n;while (n -- ){int x;cin >> x;for(int i = 2;i <= x / i;i ++){while(x % i == 0) {x /= i;primes[i] ++ ; // 指数加一}}if(x > 1) primes[x] ++;}LL res = 1;for(auto c : primes){int a = c.first,b = c.second;LL t = 1;while(b--) t = (t * a + 1) % mod;res = res * t % mod;}cout << res << endl;
}最后一步为什么会用这个t ,假设开始时为
t : 1
t :p+ 1 (t = 1 *p + 1)
t : p^2 + p +1 ( t = (p+1) * p +1 )\
....
最后t : t=p^b+p^b−1+…+1
四、求最大公约数
求最大公约数,要用到欧几里得算法,就是 gcd (a,b) = gcd(b,a%b),注意b为0的时候按照欧几里得算法,b等于0,取a;
题目
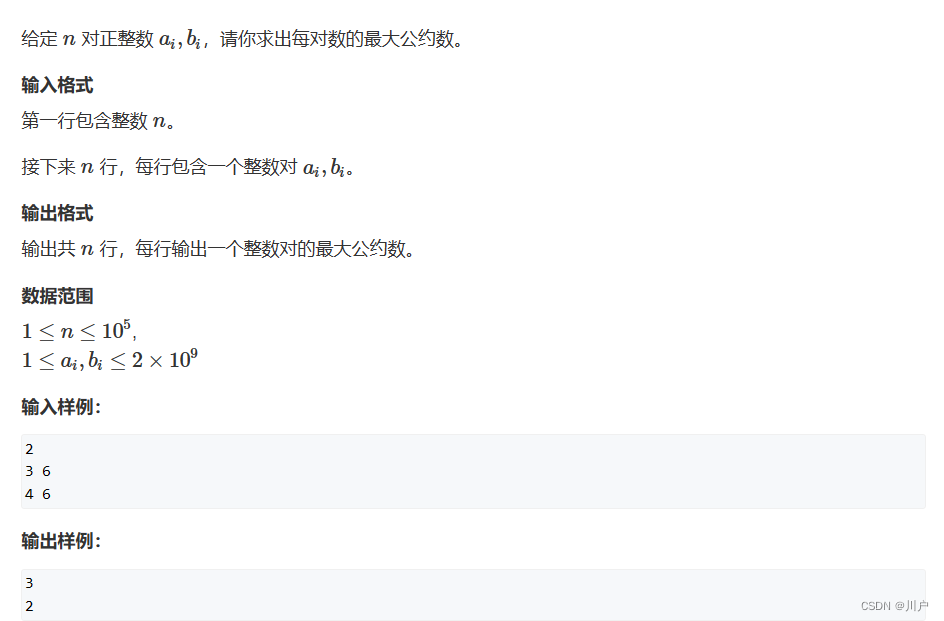
代码
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;
int gcd(int a,int b)
{return b ? gcd(b,a%b):a ; //b为0的时候按照欧几里得算法,b等于0,取a
}int main()
{int n;cin >> n;while(n --){int a,b;cin >> a >> b;int t =gcd(a,b);cout << t <<endl;}
}
三、真题演练
2020填空题
题目
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
12000001200000 有多少个约数(只计算正约数)。
运行限制
- 最大运行时间:1s
- 最大运行内存: 128M
代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
const int mod = 1e9 + 7;
typedef long long LL;
using namespace std;
int main()
{unordered_map <int,int> primes;int x;x = 1200000;for(int i = 2;i <= x / i;i ++){while(x % i == 0){x /= i;primes[i] ++;}}if(x > 1) primes[x] ++;LL res = 1;for(auto c: primes){res = res * (c.second + 1) % mod;}cout << res << endl;
}
相关文章:

蓝桥杯冲击-02约数篇(必考)
文章目录 前言 一、约数是什么 二、三大模板 1、试除法求约数个数 2、求约数个数 3、求约数之和 三、真题演练 前言 约数和质数一样在蓝桥杯考试中是在数论中考察频率较高的一种,在省赛考察的时候往往就是模板题,难度大一点会结合其他知识点考察&#x…...

122.(leaflet篇)leaflet地图图片之间存在缝隙
听老人家说:多看美女会长寿 地图之家总目录(订阅之前建议先查看该博客) 文章末尾处提供保证可运行完整代码包,运行如有问题,可“私信”博主。 存在缝隙–效果如下所示: 解决缝隙–效果如下所示: 下面献上完整代码,代码重要位置会做相应解释 <!DOCTYPE html>…...
4.类的基本概念
目录 4.1 类的概述 类是一种活动的数据结构 4.2 程序和类:一个快速实例 4.3 声明类 4.4 类成员 4.4.1 字段 1.显示和隐式字段初始化 2. 声明多个字段 4.4.2 方法 4.5 创建变量和类的实例 4.6 为数据分配内存 合并这两个步骤 4.7 实例成员 4.8 访问修饰…...
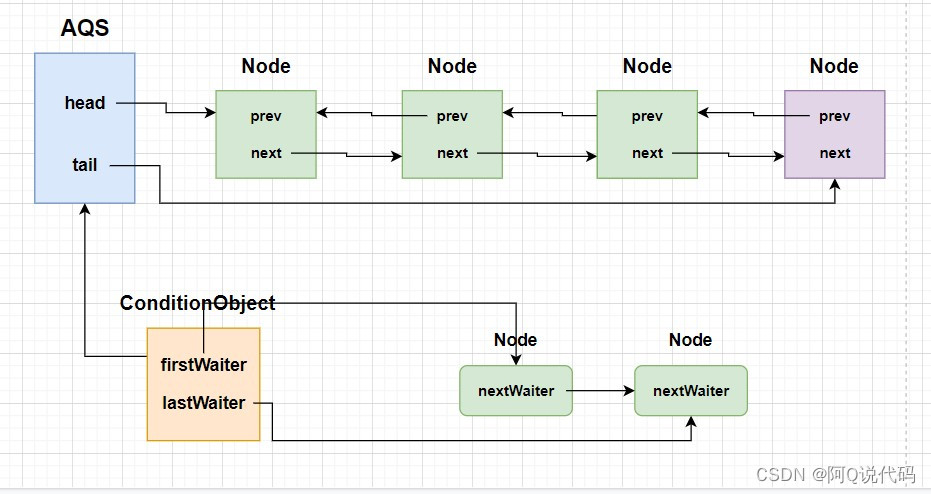
有图解有案例,我终于把 Condition 的原理讲透彻了
哈喽大家好,我是阿Q! 20张图图解ReentrantLock加锁解锁原理文章一发,便引发了大家激烈的讨论,更有小伙伴前来弹窗:平时加解锁都是直接使用Synchronized关键字来实现的,简单好用,为啥还要引用Re…...
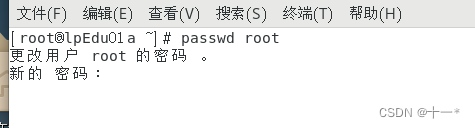
Linux之找回root密码
文章目录前言一、启动系统二、进入编辑界面三、修改密码前言 当我们使用root用户登陆Linux时,忘记了登陆密码,改怎样修改登陆密码呢,接下来将介绍如何修改root密码 一、启动系统 首先,启动系统,进入开机界面&#x…...
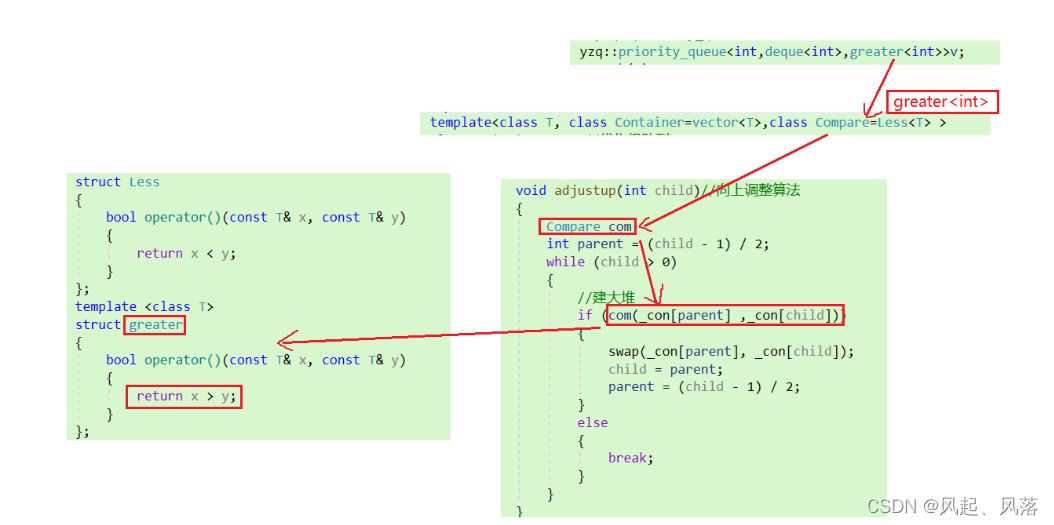
stack_queue | priority_queue | 仿函数
文章目录1. stack 的使用2. stack的模拟实现3. queue的使用4. queue的模拟实现5. deque ——双端队列deque优缺点6. priority_queue ——优先级队列1. priority_queue的使用2. priority_queue的模拟实现push——插入pop ——删除top —— 堆顶仿函数问题完整代码实现1. stack 的…...
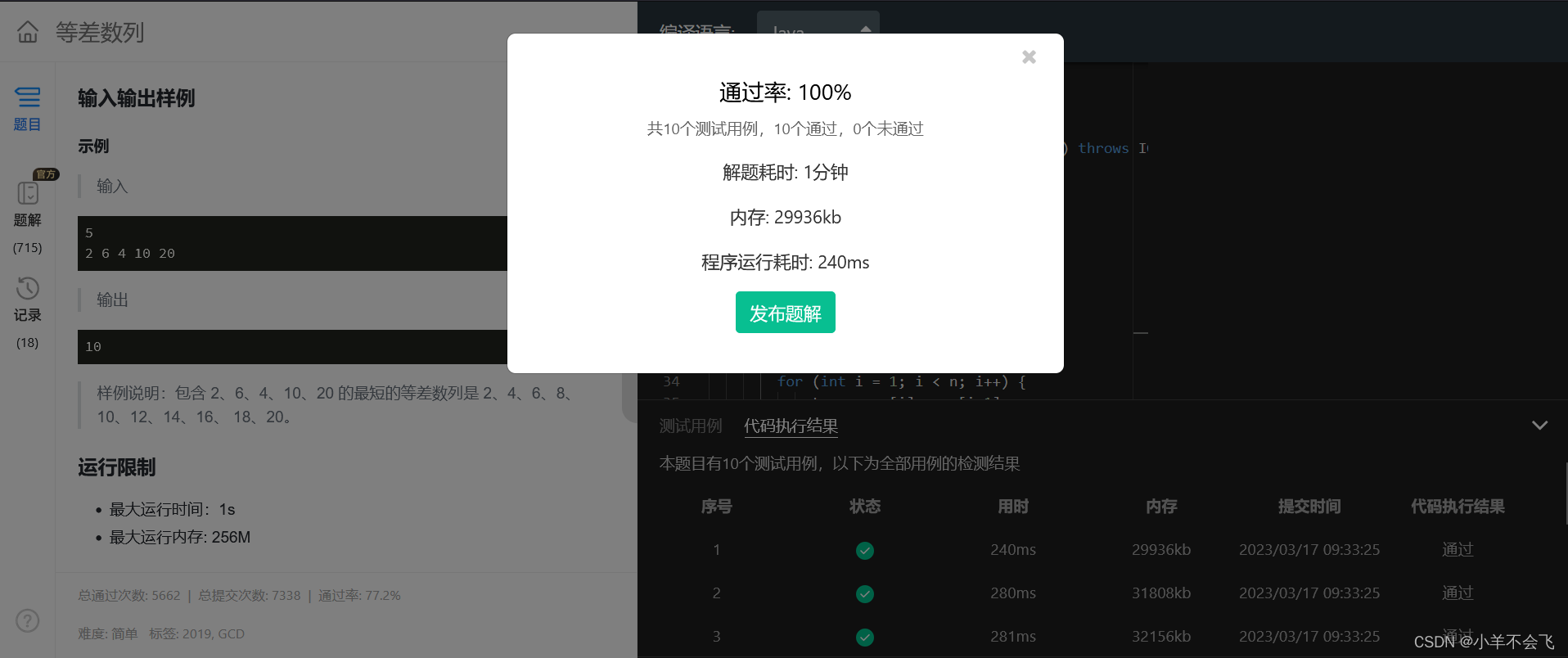
第十四届蓝桥杯三月真题刷题训练——第 14 天
目录 第 1 题:组队 题目描述 运行限制 代码: 第 2 题:不同子串 题目描述 运行限制 代码: 思路: 第 3 题:等差数列 题目描述 输入描述 输出描述 输入输出样例 运行限制 代码: 思…...
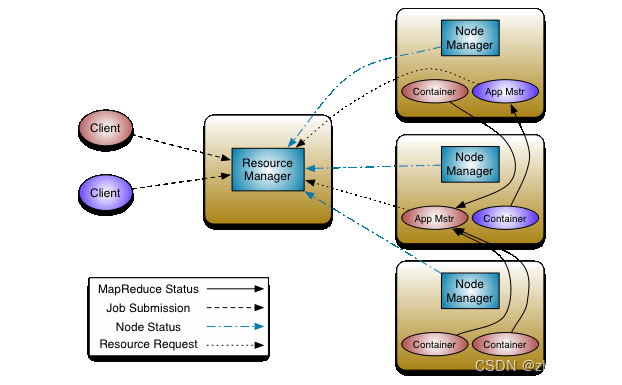
【Hadoop-yarn-01】大白话讲讲资源调度器YARN,原来这么好理解
YARN作为Hadoop集群的御用调度器,在整个集群的资源管理上立下了汗马功劳。今天我们用大白话聊聊YARN存在意义。 有了机器就有了资源,有了资源就有了调度。举2个很鲜活的场景: 在单台机器上,你开了3个程序,分别是A、B…...
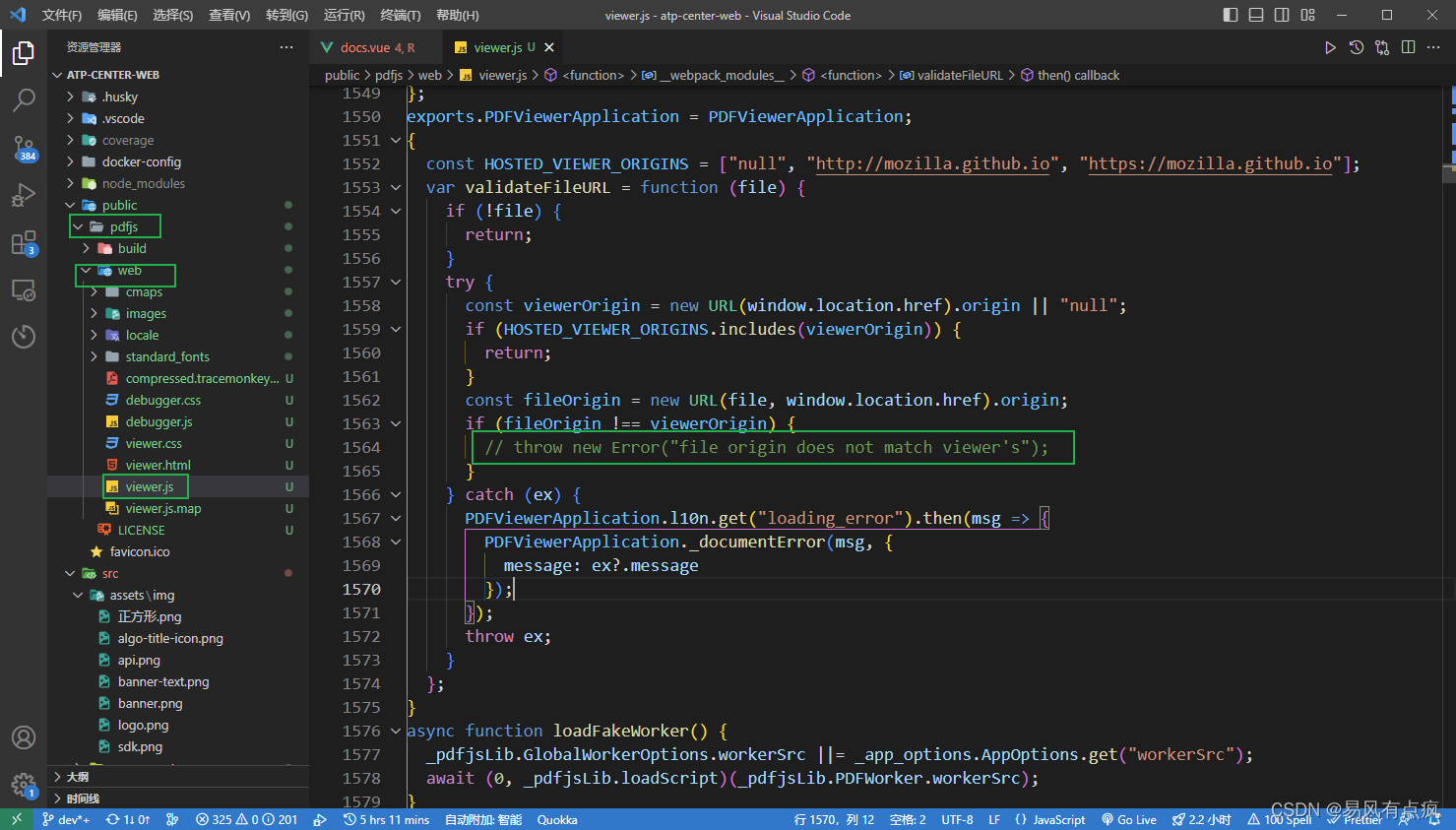
技术掉:PDF显示,使用pdf.js
PDF 显示 场景: 其实直接显示 pdf 可以用 iframe 标签,但产品觉得浏览器自带的 pdf 预览太丑了,而且无法去除那些操作栏。 解决方案:使用 pdf.js 进行显示 第一步:引入 pdf.js 去官网下载稳定版的 pdf.js 文件 然后…...
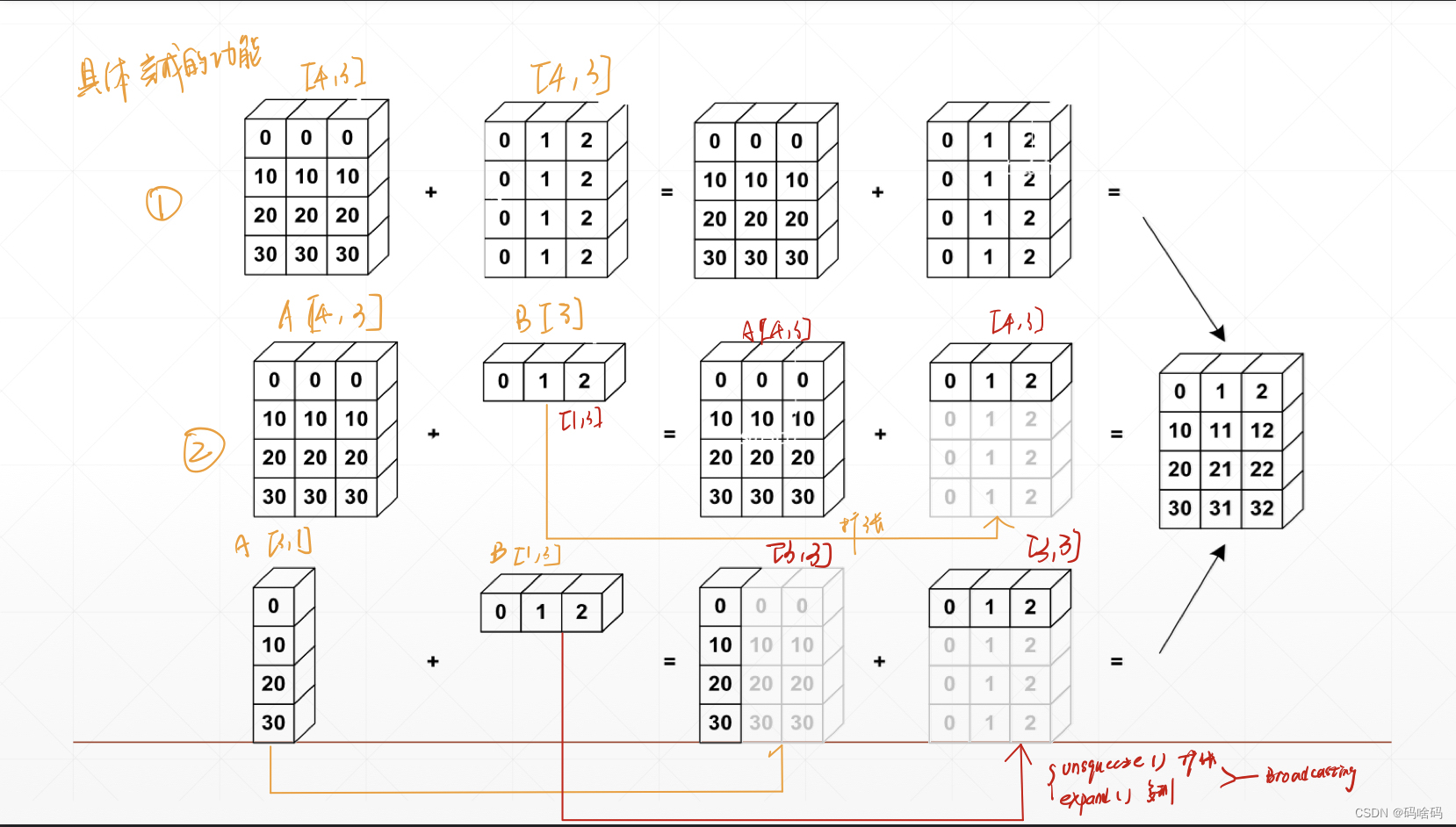
有关pytorch的一些总结
Tensor 含义 张量(Tensor):是一个多维数组,它是标量、向量、矩阵的高维拓展。 创建 非随机创建 1.用数组创建 将数组转化为tensor np.ones([a,b]) 全为1 #首先导入PyTorch import torch#数组创建 import numpy as np anp.arr…...
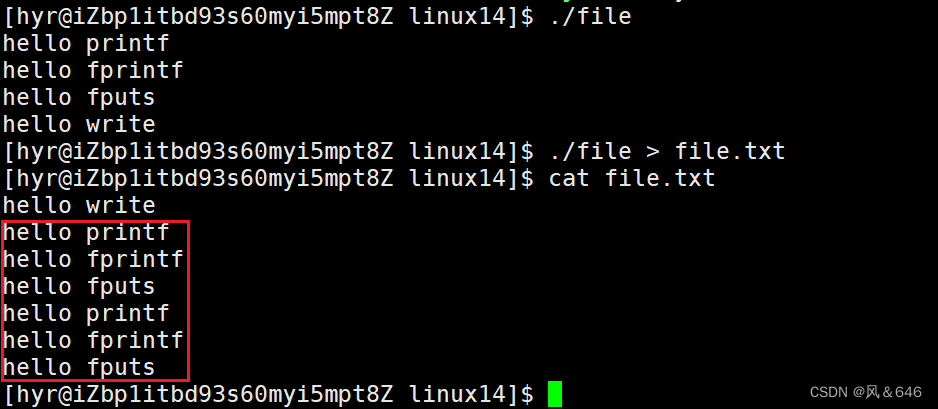
基础IO【Linux】
文章目录:文件相关知识C语言文件IOstdin & stdout & stderr系统文件 IOopenclosewriteread文件描述符文件描述符的分配规则重定向dup2系统调用FILEFILE中的文件描述符FILE中的缓冲区理解文件相关知识 文件 文件内容 文件属性(每一个已经存在的…...
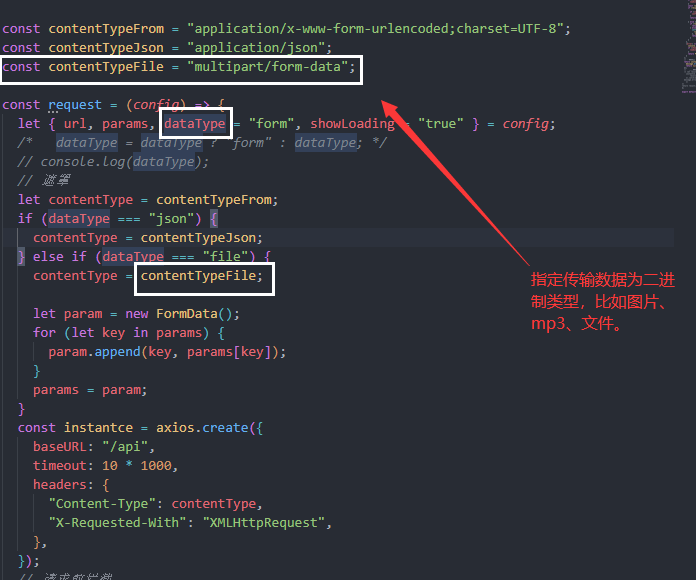
Vue3——自定义封装上传图片样式
自定义封装上传图片样式 一、首先需要新建一个自组建完善基础的结构,我这里起名为ImgUpload.vue <el-upload name"file" :show-file-list"false" accept".png,.PNG,.jpg,.JPG,.jpeg,.JPEG,.gif,.GIF,.bmp,.BMP" :multiple"…...
ChatGLM-6B (介绍以及本地部署)
中文ChatGPT平替——ChatGLM-6BChatGLM-6B简介官方实例本地部署1.下载代码2.通过conda创建虚拟环境3.修改代码4.模型量化5.详细代码调用示例ChatGLM-6B 简介 ChatGLM-6B 是一个开源的、支持中英双语问答的对话语言模型,基于 General Language Model (GLM) 架构&…...
react的基础使用
react中为什么使用jsxReact 认为渲染逻辑本质上与其他 UI 逻辑内在耦合,比如,在 UI 中需要绑定处理事件、在某些时刻状态发生变化时需要通知到 UI,以及需要在 UI 中展示准备好的数据。react认为将业务代码和数据以及事件等等 需要和UI高度耦合…...

letcode 4.寻找两个正序数组的中位数(官方题解笔记)
题目描述 给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。 算法的时间复杂度应该为 O(log (mn)) 。 1.二分查找 1.1思路 时间复杂度:O(log(mn)) 空间复杂度:O(1) 给定…...
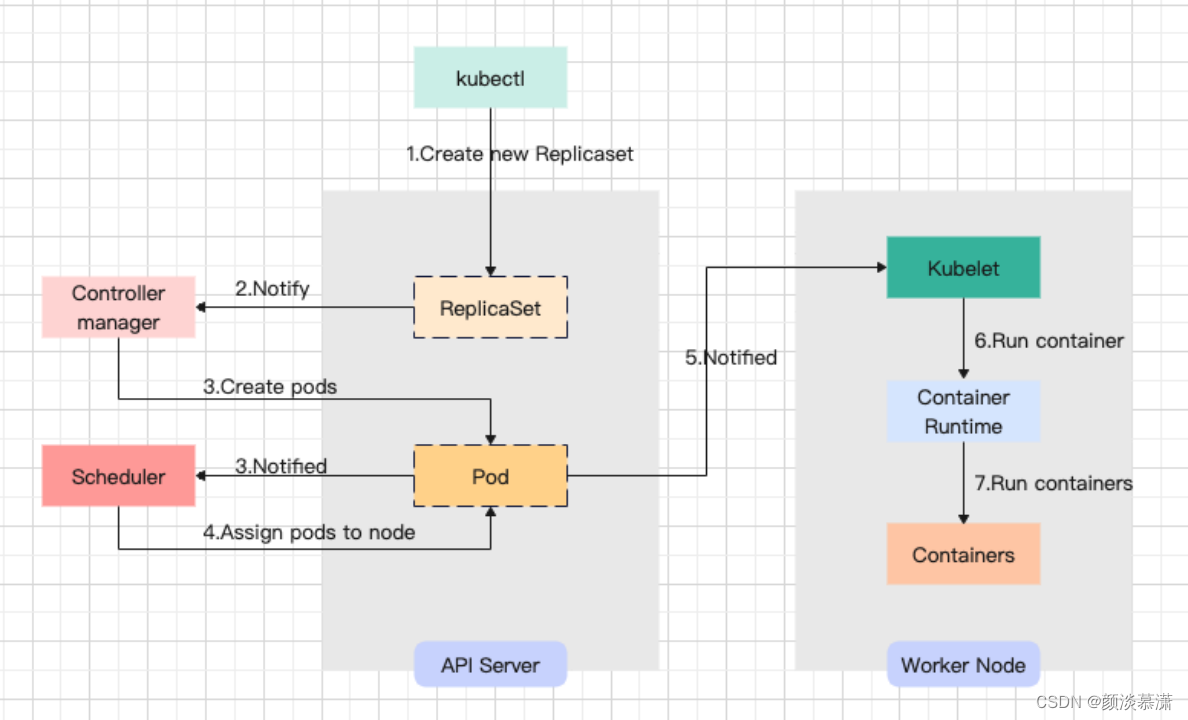
【面试题系列】K8S常见面试题
目录 序言 问题 1. 简单说一下k8s集群内外网络如何互通的吧 2.描述一下pod的创建过程 3. 描述一下k8s pod的终止过程 4.Kubernetes 中的自动伸缩有哪些方式? 5.Kubernetes 中的故障检测有哪些方式? 6.Kubernetes 中的资源调度有哪些方式ÿ…...

字符函数和字符串函数(上)-C语言详解
CSDN的各位友友们你们好,今天千泽为大家带来的是C语言中字符函数和字符串函数的详解,掌握了这些内容能够让我们更加灵活的运用字符串,接下来让我们一起走进今天的内容吧!写这篇文章需要在cplusplus.com上大量截图,十分不易!如果对您有帮助的话希望能够得到您的支持和帮助,我会持…...
全连接神经网络
目录 1.全连接神经网络简介 2.MLP分类模型 2.1 数据准备与探索 2.2 搭建网络并可视化 2.3 使用未预处理的数据训练模型 2.4 使用预处理后的数据进行模型训练 3. MLP回归模型 3.1 数据准备 3.2 搭建回归预测网络 1.全连接神经网络简介 全连接神经网络(Multi-Layer Percep…...
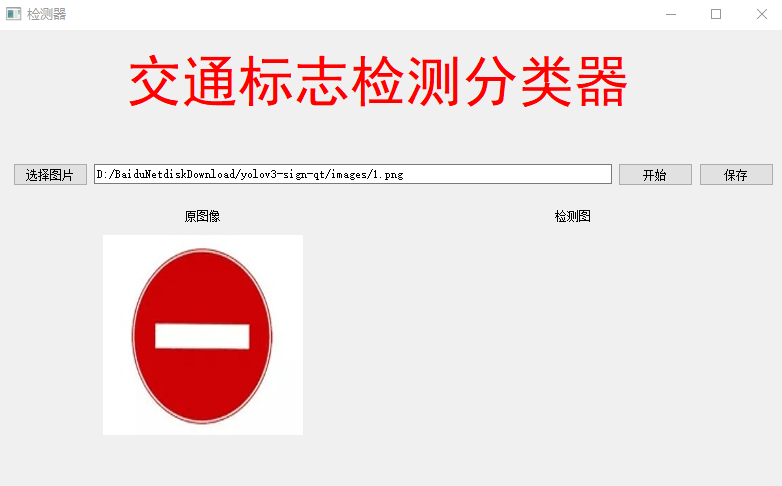
深度学习目标检测ui界面-交通标志检测识别
深度学习目标检测ui界面-交通标志检测识别 为了将算法封装起来,博主尝试了实验pyqt5的上位机界面进行封装,其中遇到了一些坑举给大家避开。这里加载的训练模型参考之前写的博客: 自动驾驶目标检测项目实战(一)—基于深度学习框架yolov的交通…...

ubuntu不同版本的源(换源)(镜像源)(lsb_release -c命令,显示当前系统的发行版代号(Codename))
文章目录查看unbuntu版本名(lsb_release -c命令)各个版本源代号(仅供参考,具体代号用上面命令查)各版本软件源Ubuntu20.10阿里源:清华源:Ubuntu20.04阿里源:清华源:Ubunt…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
