《数据结构:顺序实现二叉树》
文章目录
- 一、树
- 1、树的结构与概念
- 2、树相关术语
- 二、二叉树
- 1、概念与结构
- 2、满二叉树
- 3、完全二叉树
- 三、顺序二叉树存储结构
- 四、实现顺序结构二叉树
- 1、堆的概念与结构
- 2、堆的实现
- 3、堆的排序
一、树
1、树的结构与概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成的一个具有层次关系的集合。把它叫做树是因为它看起来像一颗倒挂的树,也就是说它是根朝上,而叶朝下的。
- 有一个特殊的结点,称为根结点,根结点没有前驱结点。
- 除根结点外,其余结点被分成 M(M>0)个互不相交的集合,其中每个集合又是一颗结构与树类似的子树。每颗自树的根结点有且只有一个 前驱,可以有0个或多个后继。因此树是递归定义的。

树形结构中,⼦树之间不能有交集,否则就不是树形结构
非树形结构:

- 子树是不相交的
- 除根结点外,每个结点有且仅有一个父节点
- 一颗N个结点的树有N - 1条边
2、树相关术语

- ⽗结点/双亲结点:若⼀个结点含有⼦结点,则这个结点称为其⼦结点的⽗结点; 如上图:A是B的⽗结点
- ⼦结点/孩⼦结点:⼀个结点含有的⼦树的根结点称为该结点的⼦结点; 如上图:B是A的孩⼦结点
- 结点的度:⼀个结点有⼏个孩⼦,他的度就是多少;⽐如A的度为6,F的度为2,K的度为0
- 树的度:⼀棵树中,最⼤的结点的度称为树的度; 如上图:树的度为 6
- 叶⼦结点/终端结点:度为 0 的结点称为叶结点; 如上图: B、C、H、I… 等结点为叶结点
- 分⽀结点/⾮终端结点:度不为 0 的结点; 如上图: D、E、F、G… 等结点为分⽀结点
- 分⽀结点/⾮终端结点:度不为 0 的结点; 如上图: D、E、F、G… 等结点为分⽀结点
- 结点的层次:从根开始定义起,根为第 1 层,根的⼦结点为第 2 层,以此类推;
- 树的⾼度或深度:树中结点的最⼤层次; 如上图:树的⾼度为 4
- 结点的祖先:从根到该结点所经分⽀上的所有结点;如上图: A 是所有结点的祖先
- 路径:⼀条从树中任意节点出发,沿⽗节点-⼦节点连接,达到任意节点的序列;⽐如A到Q的路径为:A-E-J-Q;H到Q的路径H-D-A-E-J-Q
- ⼦孙:以某结点为根的⼦树中任⼀结点都称为该结点的⼦孙。如上图:所有结点都是A的⼦孙
- 森林:由 m(m>0) 棵互不相交的树的集合称为森林;
二、二叉树
1、概念与结构
树形结构中,我们最常⽤的就是⼆叉树,⼀棵⼆叉树是结点的⼀个有限集合,该集合由⼀个根结点加上两棵别称为左⼦树和右⼦树的⼆叉树组成或者为空。

二叉树具备以下特点:
- 1.⼆叉树不存在度⼤于 2 的结点
- ⼆叉树的⼦树有左右之分,次序不能颠倒,因此⼆叉树是有序树
注意:对于任意的⼆叉树都是由以下⼏种情况复合⽽成的

2、满二叉树
⼀个⼆叉树,如果每⼀个层的结点数都达到最⼤值,则这个⼆叉树就是满⼆叉树。也就是说,如果⼀个⼆叉树的层数为 K ,且结点总数是 2k − 1 ,则它就是满⼆叉树。

3、完全二叉树
完全⼆叉树是效率很⾼的数据结构,完全⼆叉树是由满⼆叉树⽽引出来的。对于深度为 K 的,有 n 个结点的⼆叉树,当且仅当其每⼀个结点都与深度为K的满⼆叉树中编号从 1 ⾄ n 的结点⼀⼀对应时称之为完全⼆叉树。要注意的是满⼆叉树是⼀种特殊的完全⼆叉树。

二叉树性质
- 1)若规定根结点的层数为 1 ,则⼀棵⾮空⼆叉树的第i层上最多有 2i−1 个结点
- 2)若规定根结点的层数为 1 ,则深度为 h 的⼆叉树的最⼤结点数是 2h − 1
- 3)若规定根结点的层数为 1 ,具有 n 个结点的满⼆叉树的深度 h = log 2 ( n + 1 ) \log_2 (n+1) log2(n+1) ( log以2为底, n+1 为对数)
三、顺序二叉树存储结构
顺序结构存储就是使⽤数组来存储,⼀般使⽤数组只适合表⽰完全⼆叉树,因为不是完全⼆叉树会有空间的浪费,完全⼆叉树更适合使⽤顺序结构存储。

现实中我们通常把堆(⼀种⼆叉树)使⽤顺序结构的数组来存储,需要注意的是这⾥的堆和操作系统虚拟进程地址空间中的堆是两回事,⼀个是数据结构,⼀个是操作系统中管理内存的⼀块区域分段。
四、实现顺序结构二叉树
⼀般堆使⽤顺序结构的数组来存储数据,堆是⼀种特殊的⼆叉树,具有⼆叉树的特性的同时,还具备其他的特性。
1、堆的概念与结构
如果有⼀个关键码的集合K={ k 0 , k 1 , ⋯ , k n − 1 k_0, k_1, \cdots, k_{n-1} k0,k1,⋯,kn−1,把它的所有元素按完全⼆叉树的顺序存储⽅式存储,在⼀个⼀维数组中,并满⾜: K i K_i Ki<= K 2 ∗ i + 1 K_{2*i+1} K2∗i+1,i = 0、1、2… ,则称为⼩堆(或⼤堆)。将根结点最⼤的堆叫做最⼤堆或⼤根堆,根结点最⼩的堆叫做最⼩堆或⼩根堆。

堆具有以下性质
- 堆中某个结点的值总是不⼤于或不⼩于其⽗结点的值;
- 堆总是⼀棵完全⼆叉树。
顺序二叉树性质
- 对于具有 n 个结点的完全⼆叉树,如果按照从上⾄下从左⾄右的数组顺序对所有结点从0 开始编号,则对于序号为 i 的结点有:
- 若 i>0 , i 位置结点的双亲序号: (i-1)/2 ; i=0 , i 为根结点编号,⽆双亲结点
- 若 2i+1<n ,左孩⼦序号: 2i+1 , 2i+1>=n 否则⽆左孩⼦
- 若 2i+2<n ,右孩⼦序号: 2i+2 , 2i+2>=n 否则⽆右孩⼦
2、堆的实现
堆的底层结构为数组,因此定义堆的结构为:
#pragma once#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int HPDateType;typedef struct Heap
{HPDateType* arr;int capacity;int size;
}HP;//初始化
void HPInit(HP* php);//销毁
void HPDesTroy(HP* php);//堆尾插入数据
void HPPush(HP* php, HPDateType x);//向上调整
void AdjustUp(HPDateType* arr, int child);//删除堆顶数据
void HPPop(HP* php);//向下调整
void AdjustDown(HPDateType* arr, int parent,int n);//取堆顶数据
HPDateType HPTop(HP* php);//判断堆是否为空
bool HPEmpty(HP* php);
堆的函数实现:
#include"Heap.h"//初始化
void HPInit(HP* php)
{assert(php != NULL);php->arr = NULL;php->capacity = php->size = 0;
}//销毁
void HPDesTroy(HP* php)
{assert(php != NULL);free(php->arr);php->arr = NULL;php->capacity = php->size;
}//交换
void swap(HPDateType* x, HPDateType* y)
{HPDateType tmp = *x;*x = *y;*y = tmp;
}//向上调整
void AdjustUp(HPDateType* arr, int child)
{assert(arr != NULL);int parent = (child - 1) / 2;while (arr[parent] > arr[child] && child > 0){swap(&arr[parent], &arr[child]);child = parent;parent = (child - 1) / 2;}
}//插入数据
void HPPush(HP* php, HPDateType x)
{assert(php != NULL);//判断空间够不够if (php->capacity == php->size){//增容int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;HPDateType* tmp = (HPDateType*)realloc(php->arr, newcapacity*sizeof(HPDateType));if (tmp == NULL){perror("realloc fail");exit(1);}php->arr = tmp;tmp = NULL;php->capacity = newcapacity;}php->arr[php->size++] = x;AdjustUp(php->arr, php->size - 1);
}//删除数据
void HPPop(HP* php)
{assert(php != NULL);assert(php->size > 0);swap(&php->arr[0], &php->arr[php->size - 1]);php->size--;AdjustDown(php->arr, 0,php->size);
}//向下调整
void AdjustDown(HPDateType* arr, int parent,int n)
{assert(arr != NULL);int child = (parent * 2) + 1;while (child < n){if (child + 1 < n && arr[child + 1] < arr[child]){child++;}if (arr[child] < arr[parent]){swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//取堆顶数据
HPDateType HPTop(HP* php)
{assert(php != NULL);assert(php->size > 0);return php->arr[0];
}//判断堆是否为空
bool HPEmpty(HP* php)
{assert(php != NULL);return php->size == 0;
}
3、堆的排序
运用堆排序时间复杂度大大减小
void HeapSort(int* arr, int n)
{//µint i = 0;int parent = 0;int child = 0;for (i = (n - 1) / 2; i >= 0; i--){parent = i;child = parent * 2 + 1;while (child < n){if (child + 1 < n && arr[child + 1] < arr[child]){child++;}if (arr[child] < arr[parent]){int tmp = arr[child];arr[child] = arr[parent];arr[parent] = tmp;parent = child;child = parent * 2 + 1;}else{break;}}}for (i = n - 1; i > 0; i--){parent = 0;child = i;int tmp = arr[child];arr[child] = arr[parent];arr[parent] = tmp;child = parent * 2 + 1;while (child < i){if (child + 1 < i && arr[child + 1] < arr[child]){child++;}if (arr[child] < arr[parent]){tmp = arr[child];arr[child] = arr[parent];arr[parent] = tmp;parent = child;child = parent * 2 + 1;}else{break;}}}
}
相关文章:

《数据结构:顺序实现二叉树》
文章目录 一、树1、树的结构与概念2、树相关术语 二、二叉树1、概念与结构2、满二叉树3、完全二叉树 三、顺序二叉树存储结构四、实现顺序结构二叉树1、堆的概念与结构2、堆的实现3、堆的排序 一、树 1、树的结构与概念 树是一种非线性的数据结构,它是由nÿ…...

【HarmonyOS】HarmonyOS NEXT学习日记:六、渲染控制、样式结构重用
【HarmonyOS】HarmonyOS NEXT学习日记:六、渲染控制、样式&结构重用 渲染控制包含了条件渲染和循环渲染,所谓条件渲染,即更具状态不同,选择性的渲染不同的组件。 而循环渲染则是用于列表之内的、多个重复元素组成的结构中。 …...

【防火墙】防火墙NAT、智能选路综合实验
实验拓扑 实验要求 7,办公区设备可以通过电信链路和移动链路上网(多对多的NAT,并且需要保留一个公网IP不能用来转换) 8,分公司设备可以通过总公司的移动链路和电信链路访问到Dmz区的http服务器 9,多出口环境基于带宽比例进行选路…...

VUE之---slot插槽
什么是插槽 slot 【插槽】, 是 Vue 的内容分发机制, 组件内部的模板引擎使用slot 元素作为承载分发内容的出口。slot 是子组件的一个模板标签元素, 而这一个标签元素是否显示, 以及怎么显示是由父组件决定的。 VUE中slot【插槽】…...

linux、windows、macos,命令终端清屏
文章目录 LinuxWindowsmacOS 在Linux、Windows和macOS的命令终端中,清屏的命令或方法各不相同。以下是针对这三种系统的清屏方法: Linux clear命令:这是最常用的清空终端屏幕的命令之一。在终端中输入clear命令后,屏幕上的所有内容…...

【RaspberryPi】树莓派Matlab/Simulink支持包安装与使用
官网支持与兼容性 Raspberry Pi Support from MATLAB - Hardware Support - MATLAB & Simulink Raspberry Pi Support from Simulink - Hardware Support - MATLAB & Simulink Matlab与树莓派兼容性 Simulink与树莓派兼容性 树莓派Matlab&Simulink RaspberryPi支…...

嵌入式人工智能(10-基于树莓派4B的DS1302实时时钟RTC)
1、实时时钟(Real Time Clock) RTC,全称为实时时钟(Real Time Clock),是一种能够提供实时时间信息的电子设备。RTC通常包括一个计时器和一个能够记录日期和时间的电池。它可以独立于主控芯片工作ÿ…...

C++ | Leetcode C++题解之第275题H指数II
题目: 题解: class Solution { public:int hIndex(vector<int>& citations) {int n citations.size();int left 0, right n - 1;while (left < right) {int mid left (right - left) / 2;if (citations[mid] > n - mid) {right m…...

编写DockerFile
将自己的项目或者环境通过Docker部署到服务器需要一下几个步骤: 打包项目或者环境 编写Dockerfile文件 运行Dockerfile文件,构建DockerImages镜像,将DockerImages存入DockerHub或者存入阿里云镜像仓库 服务器pull下DockerImages镜像&#…...

TCP并发服务器多线程
1.创建线程‐‐pthread_create int pthread_create( pthread_t *thread, // 线程 ID 无符号长整型 const pthread_attr_t *attr, // 线程属性, NULL void *(*start_routine)(void *), // 线程处理函数 void *arg); // 线程处理函数 参数: pthrea…...

技术速递|C# 13:探索最新的预览功能
作者:Kathleen Dollard 排版:Alan Wang C# 13 已初具雏形,其新特性侧重于灵活性、性能以及使您最喜欢的功能在日常中变得更容易使用。我们以公开的方式构建 C#,在今年的 Microsoft Build 大会上,我们会让您一睹 C# 13 …...

Python设计模式:巧用元类创建单例模式!
✨ 内容: 今天我们来探讨一个高级且实用的Python概念——元类(Metaclasses)。元类是创建类的类,它们可以用来控制类的行为。通过本次练习,我们将学习如何使用元类来实现单例模式,确保某个类在整个程序中只…...

构建自主可控的工业操作系统,筑牢我国工业安全堡垒
构建自主可控的工业操作系统,筑牢我国工业安全堡垒,鸿道(Intewell)操作系统为国家工业发展保驾护航。 7月19日,全球多地安装微软操作系统的电脑设备出现大规模宕机,导致“蓝屏”现象,严重影响了航空、铁路、医疗、金…...

WPF串口通讯程序
目录 一 设计原型 二 后台源码 一 设计原型 二 后台源码 using HardwareCommunications; using System.IO.Ports; using System.Windows;namespace PortTest {/// <summary>/// Interaction logic for MainWindow.xaml/// </summary>public partial class MainW…...

汽车技术智能化程度不断提升,线束可靠性如何设计?
随着汽车技术的高速发展,汽车自动化、智能化程度的逐步提高,人们对汽车的安全性、舒适性、娱乐性等要求也不断提高,加上汽车节能减排法规的不断严峻,整车电气设备不断增加,作为连接汽车各种电器设备“神经网络”的整车…...

实现Nginx的反向代理和负载均衡
一、反向代理和负载均衡简介 1.1、反向代理 反向代理(reverse proxy)指:以代理服务器来接受Internet上的连接请求,然后将请求转发给内部网络上的服务器,并将从服务器上得到的结果返回给Internet上请求连接的客户端。此时代理服务器对外就表现为一个反向代理服务器。 反向代…...

【算法】子集
难度:中等 题目: 给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的 子集(幂集)。 解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。 示例 1: 输入:nums [1,…...

Web前端:HTML篇(一)
HTML简介: 超文本标记语言(英语:HyperText Markup Language,简称:HTML)是一种用于创建网页的标准标记语言。 您可以使用 HTML 来建立自己的 WEB 站点,HTML 运行在浏览器上,由浏览器…...

ActiViz中的选择点vtkWorldPointPicker
文章目录 1. vtkWorldPointPicker简介2. 类的位置和继承关系3. 选择机制4. 返回的信息5. 选择的条件和参数6. 与屏幕空间选择器的比较7. 性能特征8. 应用场景9. 与其他vtk选择器的集成10. 完整示例总结1. vtkWorldPointPicker简介 vtkWorldPointPicker是Visualization Toolkit…...
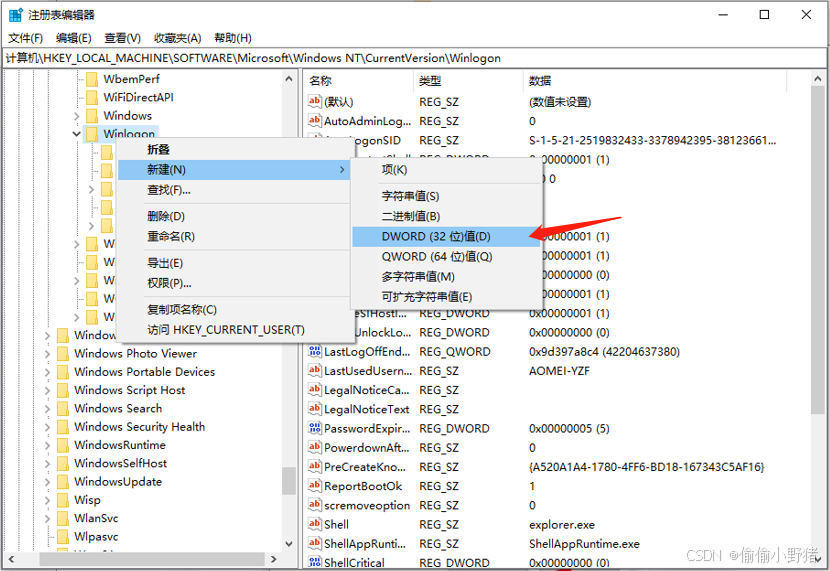
如何开启或者关闭 Windows 安全登录?
什么是安全登录 什么是 Windows 安全登录呢?安全登录是 Windows 附加的一个组件,它可以在用户需要登录的之前先将登录界面隐藏,只有当用户按下 CtrlAltDelete 之后才出现登录屏幕,这样可以防止那些模拟登录界面的程序获取密码信息…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...
