《Towards Black-Box Membership Inference Attack for Diffusion Models》论文笔记
《Towards Black-Box Membership Inference Attack for Diffusion Models》
Abstract
- 识别艺术品是否用于训练扩散模型的挑战,重点是人工智能生成的艺术品中的成员推断攻击——copyright protection
- 不需要访问内部模型组件的新型黑盒攻击方法
- 展示了在评估 DALL-E 生成的数据集方面的卓越性能。
作者主张
previous methods are not yet ready for copyright protection in diffusion models.
Contributions(文章里有三点,我觉得只有两点)
- ReDiffuse:using the model’s variation API to alter an image and compare it with the original one.
- A new MIA evaluation dataset:use the image titles from LAION-5B as prompts for DALL-E’s API [31] to generate images of the same contents but different styles.
Algorithm Design
target model:DDIM
为什么要强行引入一个版权保护的概念???
定义black-box variation API
x ^ = V θ ( x , t ) \hat{x}=V_{\theta}(x,t) x^=Vθ(x,t)
细节如下:
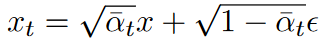
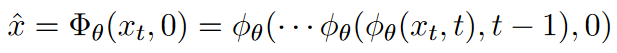
总结为: x x x加噪变为 x t x_t xt,再通过DDIM连续降噪变为 x ^ \hat{x} x^
intuition
Our key intuition comes from the reverse SDE dynamics in continuous diffusion models.
one simplified form of the reverse SDE (i.e., the denoise step)
X t = ( X t / 2 − ∇ x log p ( X t ) ) + d W t , t ∈ [ 0 , T ] (3) X_t=(X_t/2-\nabla_x\log p(X_t))+dW_t,t\in[0,T]\tag{3} Xt=(Xt/2−∇xlogp(Xt))+dWt,t∈[0,T](3)
The key guarantee is that when the score function is learned for a data point x, then the reconstructed image x ^ i \hat{x}_i x^i is an unbiased estimator of x x x.(算是过拟合的另一种说法吧)
Hence,averaging over multiple independent samples x ^ i \hat{x}_i x^i would greatly reduce the estimation error (see Theorem 1).
On the other hand, for a non-member image x ′ x' x′, the unbiasedness of the denoised image is not guaranteed.
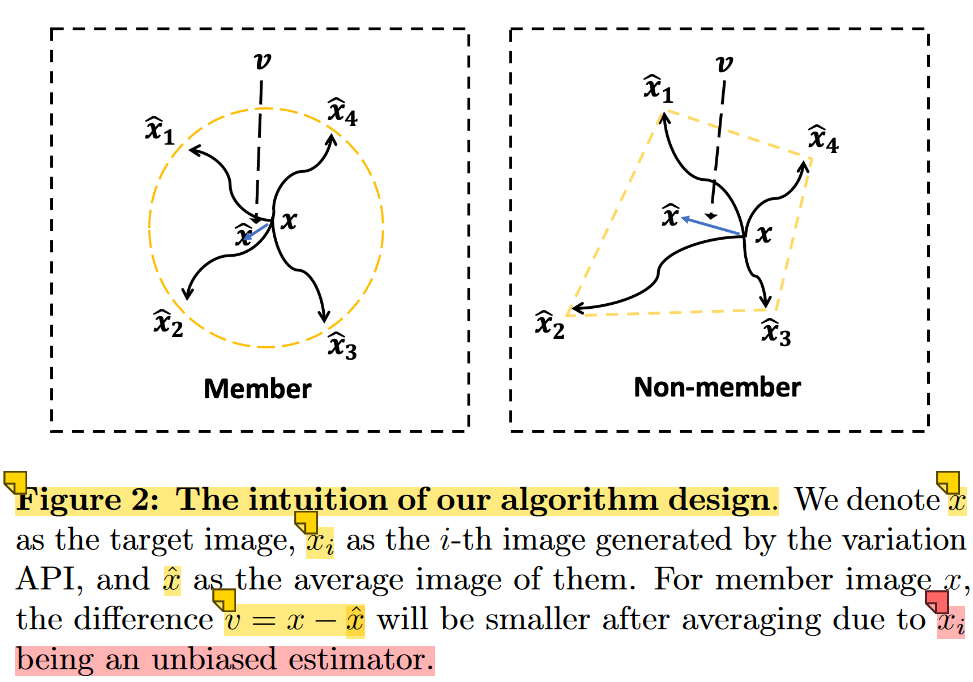
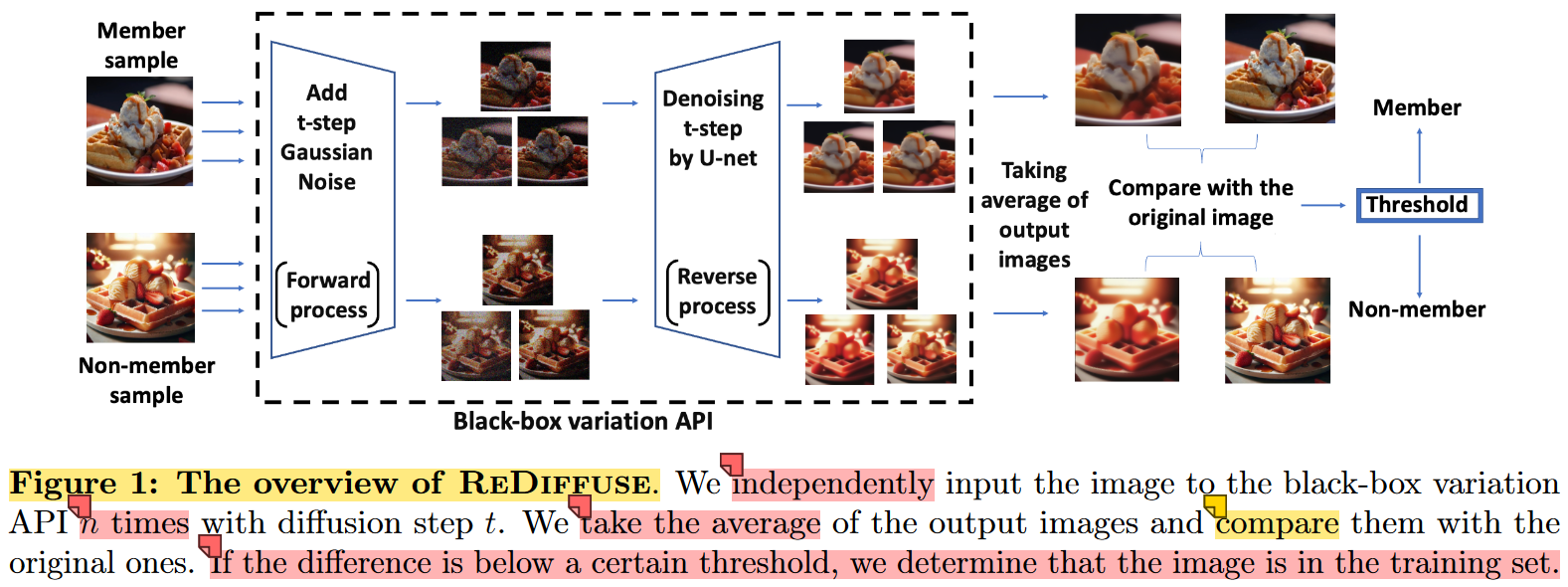
details of algorithm:
- independently apply the black-box variation API n times with our target image x as input
- average the output images
- compare the average result x ^ \hat{x} x^ with the original image.
evaluate the difference between the images using an indicator function:
f ( x ) = 1 [ D ( x , x ^ ) < τ ] f(x)=1[D(x,\hat{x})<\tau] f(x)=1[D(x,x^)<τ]
A sample is classified to be in the training set if D ( x , x ^ ) D(x,\hat{x}) D(x,x^) is smaller than a threshold τ \tau τ ( D ( x , x ^ ) D(x,\hat{x}) D(x,x^) represents the difference between the two images)
ReDiffuse
Theoretical Analysis
什么是sampling interval???
MIA on Latent Diffusion Models
泛化到latent diffusion model,即Stable Diffusion
ReDiffuse+
variation API for stable diffusion is different from DDIM, as it includes the encoder-decoder process.
z = E n c o d e r ( x ) , z t = α ‾ t z + 1 − α ‾ t ϵ , z ^ = Φ θ ( z t , 0 ) , x ^ = D e c o d e r ( z ^ ) (4) z={\rm Encoder}(x),\quad z_t=\sqrt{\overline{\alpha}_t}z+\sqrt{1-\overline{\alpha}_t}\epsilon,\quad \hat{z}=\Phi_{\theta}(z_t,0),\quad \hat{x}={\rm Decoder}(\hat{z})\tag{4} z=Encoder(x),zt=αtz+1−αtϵ,z^=Φθ(zt,0),x^=Decoder(z^)(4)
modification of the algorithm
independently adding random noise to the original image twice and then comparing the differences between the two restored images x ^ 1 \hat{x}_1 x^1 and x ^ 2 \hat{x}_2 x^2:
f ( x ) = 1 [ D ( x ^ 1 , x ^ 2 ) < τ ] f(x)=1[D(\hat{x}_1,\hat{x}_2)<\tau] f(x)=1[D(x^1,x^2)<τ]
Experiments
Evaluation Metrics
- AUC
- ASR
- TPR@1%FPR
same experiment’s setup in previous papers [5, 18].
| target model | DDIM | Stable Diffusion |
|---|---|---|
| version | 《Are diffusion models vulnerable to membership inference attacks?》 | original:stable diffusion-v1-5 provided by Huggingface |
| dataset | CIFAR10/100,STL10-Unlabeled,Tiny-Imagenet | member set:LAION-5B,corresponding 500 images from LAION-5;non-member set:COCO2017-val,500 images from DALL-E3 |
| T | 1000 | 1000 |
| k | 100 | 10 |
| baseline methods | [5]Are diffusion models vulnerable to membership inference attacks?: SecMIA | [18]An efficient membership inference attack for the diffusion model by proximal initialization. | [28]Membership inference attacks against diffusion models |
|---|---|---|---|
| publication | International Conference on Machine Learning | arXiv preprint | 2023 IEEE Security and Privacy Workshops (SPW) |
Ablation Studies
- The impact of average numbers
- The impact of diffusion steps
- The impact of sampling intervals
相关文章:

《Towards Black-Box Membership Inference Attack for Diffusion Models》论文笔记
《Towards Black-Box Membership Inference Attack for Diffusion Models》 Abstract 识别艺术品是否用于训练扩散模型的挑战,重点是人工智能生成的艺术品中的成员推断攻击——copyright protection不需要访问内部模型组件的新型黑盒攻击方法展示了在评估 DALL-E …...

vscode调试nextjs前端后端程序、nextjs api接口
最近有一个项目使用了nextjs框架,并且使用nextjs同时实现了前后端,由于之前前后端都是分离的,前端的调试可以通过在代码种添加debugger或者直接在浏览器中打断点实现,现在想调试后端接口,前面的方式就不适用了。故研究…...

《SeTformer Is What You Need for Vision and Language》
会议:AAAI 年份:2024 论文:DDAE: Towards Deep Dynamic Vision BERT Pretraining - AMinerhttps://www.aminer.cn/pub/6602613613fb2c6cf6c387c2/ddae-towards-deep-dynamic-vision-bert-pretraining 摘要 这篇论文介绍了一种新型的变换器…...

[保姆级教程]uniapp安装使用uViewUI教程
文章目录 创建 UniApp 项目下载uView UI下载安装方式步骤 1: 安装 uView UI步骤 2: 查看uView UI是否下载成功步骤 3: 引入 uView 主 JS 库步骤 4: 引入 uView 的全局 SCSS 主题文件步骤 5: 引入 uView 基础样式步骤 6: 配置 easycom 组件模式注意事项 NPM方式步骤 1: 安装 uVi…...

网络安全法规对企业做等保有哪些具体规定?
网络安全法规对企业做等保的具体规定 根据《中华人民共和国网络安全法》,企业作为网络运营者,需要履行网络安全等级保护制度的相关义务,确保网络安全和数据保护。具体规定包括: 网络安全等级保护制度:企业应根据网络安…...

Java开发中超好用Orika属性映射工具
Orika属性映射工具 引入pom依赖 <dependency><groupId>ma.glasnost.orika</groupId><artifactId>orika-core</artifactId><version>1.5.4</version></dependency>上干货 封装的工具类:OriUtilsimport ma.glasnost.orika.Map…...

qt初入门8:下拉框,输入框模糊查询,提示简单了解 (借助QCompleter)
实现一个简单的模糊查询的逻辑,输入框能提示相关项。 主要借助qt的QCompleter 类( Qt 框架中提供的一个用于自动补全和模糊搜索的类),结合一些控件,比如QComboBox和QLineEdit,实现模糊查询的功能。 1&…...

【qt】VS中如何配置Qt环境
https://download.qt.io/official_releases/vsaddin/ 首先需要下载一下vsaddin,上面的是下载的网站. 下载的时候可能会出现下图的情况 说明你下的vsaddin和您的VS版本不匹配,所以你可以多下几个其他版本的vsAddin,一般都是和你VS版本相匹配的才可以,如Vs2022,那就试试vsaddin2…...

对于相同网段的IP,部分无法ping通问题
现象1:在Linux上执行 ping 192.168.1.232,无法ping通 分析1:使用ifconfig查询,联网使用eth0口,只能上网192.168.10.xx网段,需要增加网段 解决方法:使用ip addr 查询,本身只具备10网…...
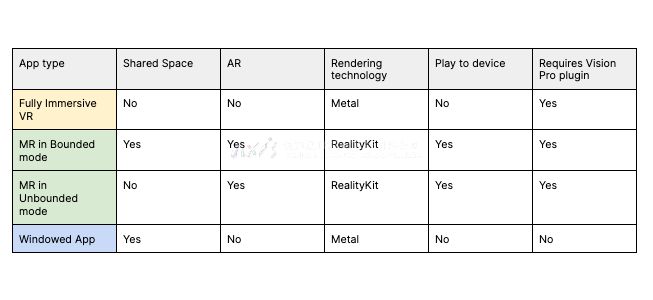
Unity发布XR中用于worldbuilding的全新电子书
通过身临其境的虚拟领域开始旅程,在维度之间传送,或将数字奇迹与现实世界融合——虚拟现实(VR)和混合现实(MR)的千万种可能性将邀请创作者把他们的想象力带入生活。 Unity发布的最新版综合指南将帮助有抱负的创作者和经验丰富的开发者深入研究和理解构建…...

Vue3相比于Vue2进行了哪些更新
1、响应式原理 vue2 vue2中采用 defineProperty 来劫持整个对象,然后进行深度遍历所有属性,给每个属性添加getter和setter,结合发布订阅模式实现响应式。 存在的问题: 检测不到对象属性的添加和删除数组API方法无法监听到需要对…...

Unity UGUI 之 Slider
本文仅作学习笔记与交流,不作任何商业用途 本文包括但不限于unity官方手册,唐老狮,麦扣教程知识,引用会标记,如有不足还请斧正 1.Slider是什么 滑块,由三部分组成:背景 填充条 手柄 填充条就是…...

这7款高效爬虫工具软件,非常实用!
在当今数据驱动的时代,自动化爬虫工具和软件成为了许多企业和个人获取数据的重要手段。这里会介绍6款功能强大、操作简便的自动化爬虫工具,用好了可以更高效地进行数据采集。 1. 八爪鱼采集器 八爪鱼是一款功能强大的桌面端爬虫软件,主打可…...

【OJ】二叉树相关OJ题
✨✨欢迎大家来到Celia的博客✨✨ 🎉🎉创作不易,请点赞关注,多多支持哦🎉🎉 所属专栏:OJ题 个人主页:Celias blog~ 目录 编辑 单值二叉树 题目描述 OJ-单值二叉树 解题思路 …...

Blender中保存透明图片
在Blender中保存透明图片,主要是通过在渲染设置中调整背景透明度,并选择合适的文件格式来保存图像。以下是一个详细的步骤指南: 一、设置渲染属性 打开Blender并加载你想要渲染的模型。在右侧的属性编辑器中,找到并点击“渲染属…...

MySQL之索引优化
1、在进行查询时,索引列不能是表达式的一部分,也不能是函数的参数,否则无法使用索引 例如下面的查询不能使用 actor_id 列的索引: #这是错误的 SELECT actor_id FROM sakila.actor WHERE actor_id 1 5; 优化方式:…...

Spring Boot 与 Amazon S3:快速上传与下载文件的完整指南
概要 在将 Spring Boot 更新到 3 系列时,由于 javax 需要被替换为 jakarta,因此原先依赖于 javax 的 spring-cloud-starter-aws1 将无法使用(虽然在我本地环境中仍然可以正常工作)。为了确保兼容性,我将依赖关系更改为…...
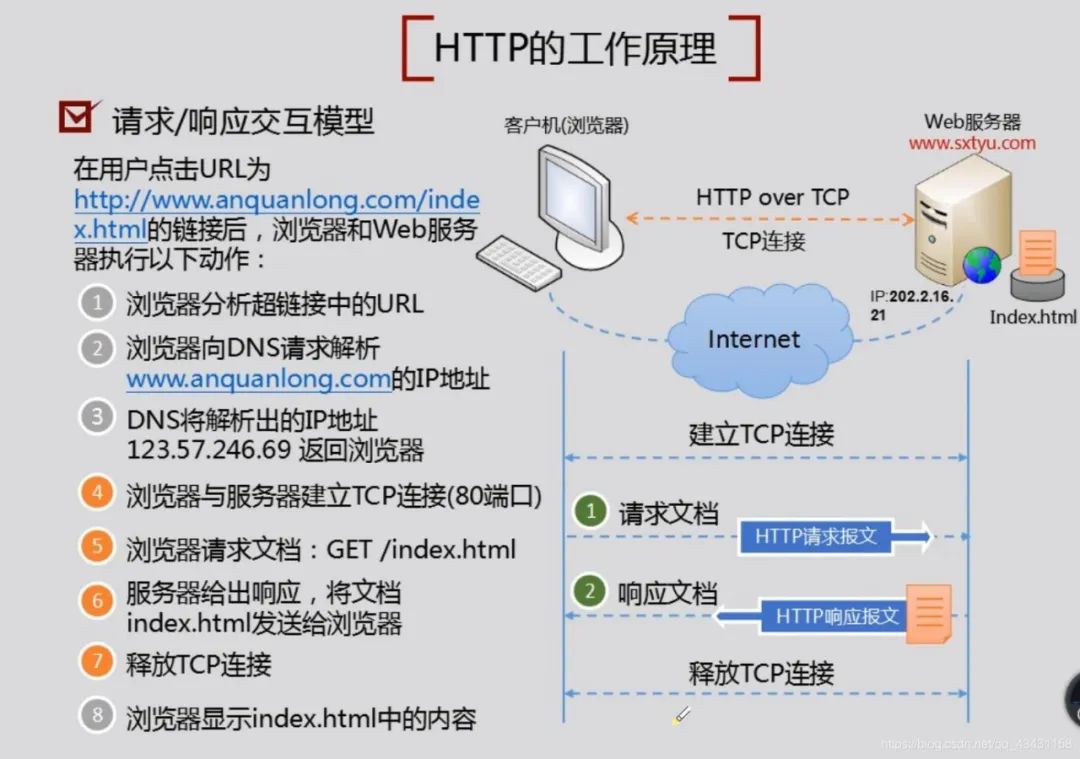
细节剖析:HTTP与HTTPS在安全性、性能等方面的不同!
HTTPS是现代互联网通信的重要基石,通过加密通信、身份验证和数据完整性保护,为数十亿用户提供了安全可靠的互联网体验。 小编整理了2GB程序员相关资料,关注微信公众号“程序员Style”回复“程序员”免费领取! 1、介绍 随着 HTT…...

MySQL面试篇章——MySQL索引
文章目录 MySQL 索引索引分类索引创建和删除索引的执行过程explain 查看执行计划explain 结果字段分析 索引的底层实现原理B-树B树哈希索引 聚集和非聚集索引MyISAM(\*.MYD,*.MYI)主键索引辅助索引(二级索引) InnoDB&a…...

WSL 2 Oracle Linux 9.1 安装配置
文章目录 环境使用体验安装 Oracle Linux 9.1修改默认存储路径默认 root 用户登录启用 systemd启用 SSH 连接WSL 无法 ping 通宿主机和域名WSL 使用主机代理(测试通过)WSL 常用命令 环境 OS:Win11 24H2 (OS 内部版本26120.1252) wsl --versio…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
