LeetCode-day23-3098. 求出所有子序列的能量和
LeetCode-day23-3098. 求出所有子序列的能量和
- 题目描述
- 示例
- 示例1:
- 示例2:
- 示例3:
- 思路
- 代码
题目描述
给你一个长度为 n 的整数数组 nums 和一个 正 整数 k 。
一个 子序列的 能量 定义为子序列中 任意 两个元素的差值绝对值的 最小值 。
请你返回 nums 中长度 等于 k 的 所有 子序列的 能量和 。
由于答案可能会很大,将答案对 109 + 7 取余 后返回。
示例
示例1:
输入:nums = [1,2,3,4], k = 3
输出:4
解释:
nums 中总共有 4 个长度为 3 的子序列:[1,2,3] ,[1,3,4] ,[1,2,4] 和 [2,3,4] 。能量和为 |2 - 3| + |3 - 4| + |2 - 1| + |3 - 4| = 4 。
示例2:
输入:nums = [2,2], k = 2
输出:0
解释:
nums 中唯一一个长度为 2 的子序列是 [2,2] 。能量和为 |2 - 2| = 0 。
示例3:
输入:nums = [4,3,-1], k = 2
输出:10
解释:
nums 总共有 3 个长度为 2 的子序列:[4,3] ,[4,-1] 和 [3,-1] 。能量和为 |4 - 3| + |4 - (-1)| + |3 - (-1)| = 10 。
思路
子序列问题的拆解 + 前缀和优化
代码
MOD = 10**9+7class Solution:def sumOfPowers(self, a: List[int], k: int) -> int:n = len(a)a.sort()def calc(dist_from_center: List[int], limit_lo: int) -> int:m = len(dist_from_center) # 从中心点算起的距离f = [[0] * k for _ in range(m)] # f[i][j]: 取到第i个元素时,拿j个物品的方法数f[0][1] = 1 # 背包问题方案数f_acc = [[0] * k for _ in range(m + 1)] # f_acc[i][j]: 物品[0, i-1], 拿j物品的方法数f_acc[1][1] = 1pt = 0for i in range(1, m):while pt < i and dist_from_center[i] - dist_from_center[pt] >= limit_lo:pt += 1for v in range(k - 1):f[i][v + 1] = (f[i][v + 1] + f_acc[pt][v]) % MODfor v in range(k):f_acc[i + 1][v] = (f_acc[i][v] + f[i][v]) % MODreturn f_acc[-1] # 物品[0, m]之方法数ans = 0for i in range(n):for j in range(i):min_diff = a[i] - a[j] # 最小差值dist_left = [a[j] - a[k] for k in range(j, -1, -1)] # 注意取距离中心点的距离,要包含自己!f_left = calc(dist_left, min_diff + 1) # 左右随便找一个不包含,都不会重复dist_right = [a[k] - a[i] for k in range(i, n)]f_right = calc(dist_right, min_diff)for x in range(1, k): # 枚举左右取多少,左右至少取一个ans = (ans + min_diff * f_left[x] * f_right[k - x]) % MODreturn ans
相关文章:

LeetCode-day23-3098. 求出所有子序列的能量和
LeetCode-day23-3098. 求出所有子序列的能量和 题目描述示例示例1:示例2:示例3: 思路代码 题目描述 给你一个长度为 n 的整数数组 nums 和一个 正 整数 k 。 一个 子序列的 能量 定义为子序列中 任意 两个元素的差值绝对值的 最小值 。 请…...
CSS3雷达扫描效果
CSS3雷达扫描效果https://www.bootstrapmb.com/item/14840 要创建一个CSS3的雷达扫描效果,我们可以使用CSS的动画(keyframes)和transform属性。以下是一个简单的示例,展示了如何创建一个类似雷达扫描的动画效果: HTM…...

单例模式懒汉模式和饿汉模式
线程安全 单例模式在单线程中,当然是安全的。但是如果在多线程中,由于并行判断,可能会导致创建多个实例。那么如何保证在多线程中单例还是只有一个实例呢? 常见的三种方式: 局部静态变量 原理和饿汉模式相似,利用static只会初始…...

python __repr__和__str__区别
1. __repr__ __repr__ 方法由 repr() 内置函数调用,用于计算对象的“正式”字符串表示形式。理想情况下,这个字符串应该看起来像一个有效的 Python 表达式,可以在适当的环境下用来重新创建具有相同值的对象。如果这不可能实现,那…...

huawei USG6001v1学习----NAT和智能选路
目录 1.NAT的分类 2.智能选路 1.就近选路 2.策略路由 3.智能选路 NAT:(Network Address Translation,网络地址转换) 指网络地址转换,1994年提出的。NAT是用于在本地网络中使用私有地址,在连接互联网时转而使用全局…...

FPGA JTAG最小系统 EP2C5T144C8N
FPGA的文档没有相应的基础还真不容易看懂,下面是B站上对FPGA文档的解读(本文非对文档解读,只是为个人记录第三期:CycloneIV E最小系统板设计(一)从Datasheet上获取FPGA的基本参数_哔哩哔哩_bilibili 电源部份 核心电…...

Android 15 之如何快速适配 16K Page Size
在此之前,我们通过 《Android 15 上 16K Page Size 为什么是最坑》 介绍了: 什么是16K Page Size为什么它对于 Android 很坑如何测试 如果你还没了解,建议先去了解下前文,然后本篇主要是提供适配的思路,因为这类适配…...

学习unity官方的网络插件Netcode【一】
对bool值的个人理解: using Unity.Netcode; using UnityEngine; //个人理解:通过Rpc完成了一次客户端给服务端发消息,服务端再向所有客户端广播消息 public class RpcTest : NetworkBehaviour {public override void OnNetworkSpawn(){if (!…...

QT写一个mainWindow
切换风格的写法: 先看看样式效果: mian_window.h文件 #ifndef MAINWINDOW_H #define MAINWINDOW_H#include <QMainWindow>class MainWindow : public QMainWindow {Q_OBJECTpublic:MainWindow(QWidget *parent nullptr);~MainWindow();void Ini…...
)
Java查找算法练习(2024.7.23)
顺序查找 package SearchExercise20240723; import java.util.Scanner; public class SearchExercise {public static void main(String[] args) {Scanner sc new Scanner(System.in);System.out.println("需要多大的数组?");int size sc.nextInt();int[] array …...

洗地机哪个牌子好?四款口碑最好的洗地机排名推荐
随着“懒人经济”的出现,越来越多的人开始使用洗地机。洗地机哪个牌子好?为了帮助大家在这个琳琅满目的市场中做出明智决策,本文特别整理了四款口碑最好的洗地机排名推荐,它们凭借出色的清洁效果、智能化的操作体验以及用户的高度…...

如何提升短视频的曝光量和获客效能?云微客来解决
在流量至上的当下,短视频凭借其优势,迅速成为了众多企业获客引流的核心营销手段。进入短视频赛道后,如何提升短视频的曝光量和获客效能,就成为了众多企业亟待解决的焦点。 如果你不想投入大量的广告预算,还想在短视频平…...

SpringBoot开发中如何缓存数据, 减少数据库的访问频率?
一:自定义是否开启缓存 方法一: 在不同环境的配置文件中如application-dev.yml、application-test.yml、application-prod.yml,修改 spring.cache.type none; spring:cache:type: none 方法二: 自定义配置 application.yml&…...

PostgreSQL如何在windows/linux开启归档
linux开启归档: archive_mode onarchive_command test ! -f /mnt/pg12/archivedir/%f && cp %p /mnt/pg12/archivedir/%fwindows开启归档: archive_mode onarchive_command copy "%p" "C:\\server\\pg12\\archivedir\\%f&q…...

【启明智显分享】基于国产Model3芯片的7寸触摸屏助力智慧医疗,电子床头屏提升护理交互
未来医院必然是以信息化为基础,以物联网为特征,以医疗为核心的服务型医院。病房作为医院的重要服务场所,成为智慧医院建设的重要一环。 为提高医护人员与患者的互动交流,给医疗注入智慧元素,让患者享受智能服务&#…...

从理论到实践:如何用 TDengine 打造完美数据模型
在用 TDengine 进行数据建模之前,我们需要回答两个关键问题:建模的目标用户是谁?他们的具体需求是什么?在一个典型的时序数据管理方案中,数据采集和数据应用是两个主要环节。如下图所示: 对于数据采集工程师…...

可以免费合并pdf的软件 合并pdf文件的软件免费 合并pdf的软件免费
在数字化办公的今天,pdf格式因其稳定性和跨平台兼容性被广泛使用。然而,当我们需要将多个 pdf 文件合并为一个时,却往往感到力不从心。本文将为你介绍几款强大的pdf文件合并软件,让你轻松管理文档。 方法一、使用pdf转换器 步骤1…...

【排序 滑动窗口 】1498. 满足条件的子序列数目
本文涉及至知识点 排序 C算法:滑动窗口总结 LeetCode1498. 满足条件的子序列数目 给你一个整数数组 nums 和一个整数 target 。 请你统计并返回 nums 中能满足其最小元素与最大元素的 和 小于或等于 target 的 非空 子序列的数目。 由于答案可能很大,…...

RabbitMQ普通集群搭建指南
RabbitMQ普通集群搭建指南 本文已经完全迁移至,www.geekery.cn 后续不在此更新 目标架构 本次搭建的目标是构建一个由三个节点组成的RabbitMQ集群,节点信息如下: rabbit02: IP地址 192.168.10.132rabbit03: IP地址 192.168.10.133rabbit04:…...

AGV平面坐标系变换公式及实例
1、AGV坐标系简介 如上图,小车前后对角是有激光雷达的,其坐标系称为激光坐标系,采用极坐标系体现。中间为车体坐标系,激光坐标系相对于车体坐标系关系不变;左下角是地图坐标系,小车扫图后,建立的…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

轻量级Docker管理工具Docker Switchboard
简介 什么是 Docker Switchboard ? Docker Switchboard 是一个轻量级的 Web 应用程序,用于管理 Docker 容器。它提供了一个干净、用户友好的界面来启动、停止和监控主机上运行的容器,使其成为本地开发、家庭实验室或小型服务器设置的理想选择…...
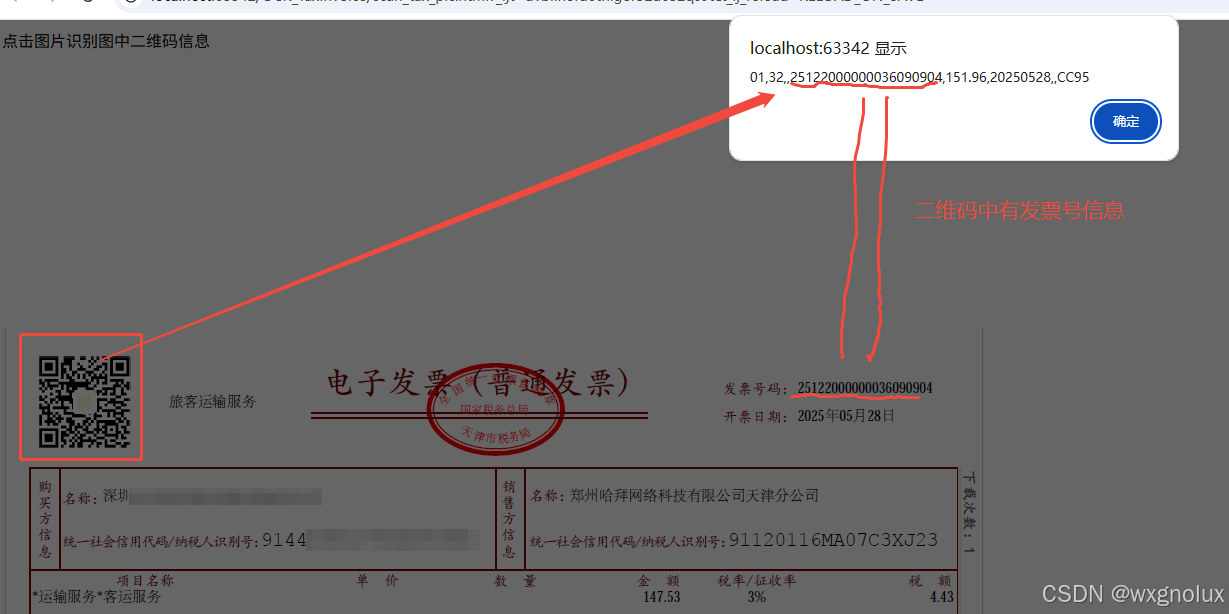
网页端 js 读取发票里的二维码信息(图片和PDF格式)
起因 为了实现在报销流程中,发票不能重用的限制,发票上传后,希望能读出发票号,并记录发票号已用,下次不再可用于报销。 基于上面的需求,研究了OCR 的方式和读PDF的方式,实际是可行的ÿ…...
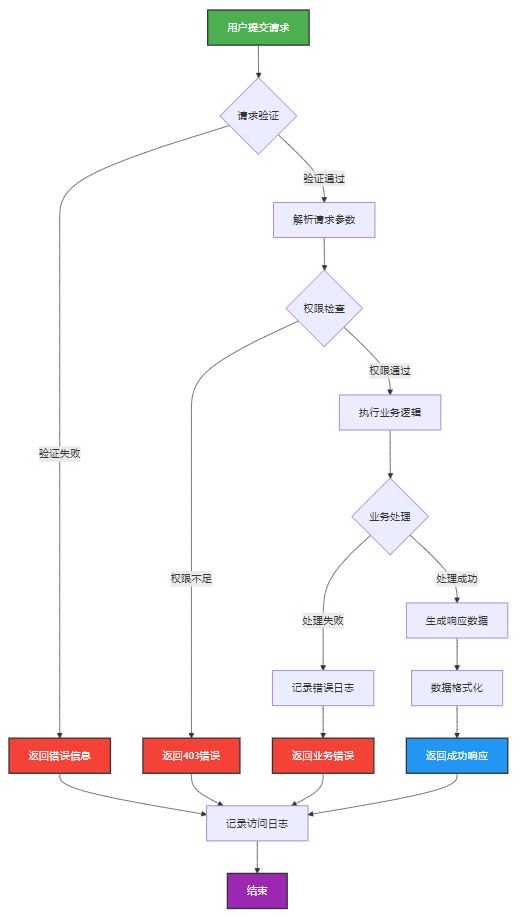
如何做好一份技术文档?从规划到实践的完整指南
如何做好一份技术文档?从规划到实践的完整指南 🌟 嗨,我是IRpickstars! 🌌 总有一行代码,能点亮万千星辰。 🔍 在技术的宇宙中,我愿做永不停歇的探索者。 ✨ 用代码丈量世界&…...
C++中vector类型的介绍和使用
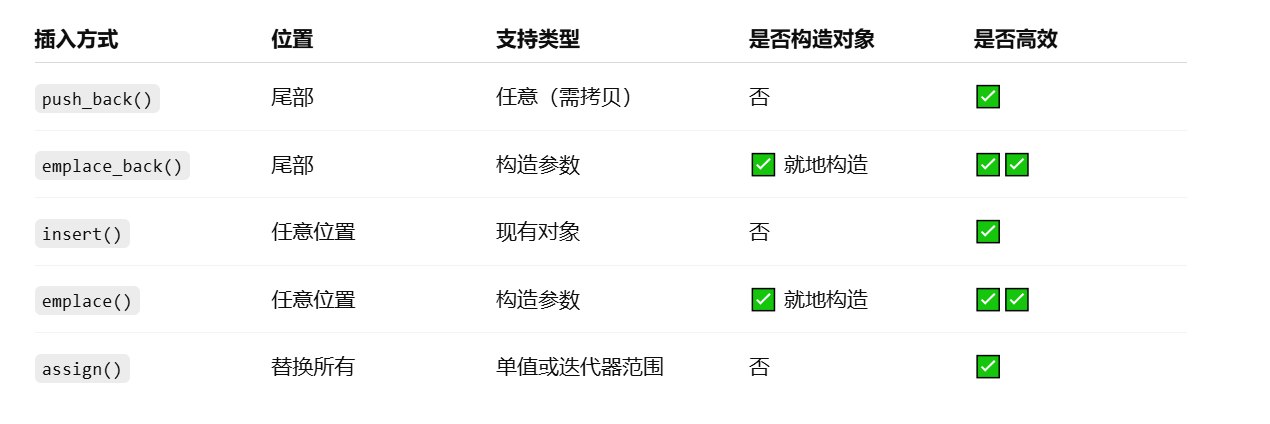
文章目录 一、vector 类型的简介1.1 基本介绍1.2 常见用法示例1.3 常见成员函数简表 二、vector 数据的插入2.1 push_back() —— 在尾部插入一个元素2.2 emplace_back() —— 在尾部“就地”构造对象2.3 insert() —— 在任意位置插入一个或多个元素2.4 emplace() —— 在任意…...
