迭代学习笔记
一、迭代学习定义和分类
1、直观理解
- 迭代学习一般应用于重复性的场景。比如控制一个单自由度的小车以特定的速度曲线移动到指定位置,整个时间是10s,控制频率是0.01,那么整个控制序列就会有1000个点。这1000个点在10s内依次发出,完成依次控制,目的就是让小车的速度或者位置跟踪上特定的曲线。我们有一个优势在于跟踪曲线不变,那么我们可以不断进行尝试,只要获得一组良好的控制序列,那么就可以完成控制。
2、更新率
-
如果我们可以设置一个更新率,根据每一个点面临的误差对控制量进行修改,那么就可以在若干次更新后获得完美的控制序列。
新控制量 = 旧控制量 + 更新率 新控制量 = 旧控制量 + 更新率 新控制量=旧控制量+更新率 -
根据更新率与什么参数有关,可以分为开环、闭环、开闭环。如果跟上一次的误差有关就是开环,如果跟此刻的误差有关就是闭环,如果都有关就是开闭环。根据更新率的结构还可以分为D型、PD型等。
-
需要注意一下有D型和PD型,没有P型,我在仿真中试了半天P型都不收敛。
二、实现例子
- 网上关于迭代学习的代码实现比较少,很多还是用simulink搭的,不方便复现。这里给一个D型闭环迭代学习例子,被控对象是一个钟摆小车,全部代码用python实现,直接运行即可。

1、动力学模型
# 动力学模型函数
def dynamics(state, u):x, theta, dx, dtheta = statedd_x = (u + m2*l*dtheta*dtheta + m2*g*np.sin(theta)*np.cos(theta)) / (m1 + m2*np.sin(theta)*np.sin(theta))dd_theta = (-dd_x*np.cos(theta) + dx*np.sin(theta)*dtheta - np.sin(theta)*(dx*dtheta + g)) / lreturn np.array([dx, dtheta, dd_x, dtheta])
2、四阶龙格库塔积分器和控制器更新率
# 四阶龙格库塔法函数
def RK4(t_start, t_end, fun, Npoints, init_state, u_list, pos_des, spd_des):t = np.linspace(t_start, t_end, Npoints)dt = t[1] - t[0]state = np.zeros((Npoints, len(init_state)))state[0, :] = init_statee = np.zeros((Npoints, 2))for i in range(Npoints-1):u_list[i] = u_list[i] + 1 * (spd_des[i] - state[i, 2]) # 闭环D型更新率u = u_list[i]e[i, 0] = pos_des[i] - state[i, 0]e[i, 1] = spd_des[i] - state[i, 2]k1 = fun(state[i, :], u)k2 = fun(state[i, :] + 0.5 * dt * k1, u)k3 = fun(state[i, :] + 0.5 * dt * k2, u)k4 = fun(state[i, :] + dt * k3, u)state[i + 1, :] = state[i, :] + (1/6) * dt * (k1 + 2 * k2 + 2 * k3 + k4)return state, u_list, e
3、进行迭代
for i in range(10):# 运行RK4state, u_list, e_buff = RK4(t_start, t_end, dynamics, Npoints, [0, 0, 0, 0], u_list, pos_des, spd_des)
4、完整代码和效果展示
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd# 动力学模型函数
def dynamics(state, u):x, theta, dx, dtheta = statedd_x = (u + m2*l*dtheta*dtheta + m2*g*np.sin(theta)*np.cos(theta)) / (m1 + m2*np.sin(theta)*np.sin(theta))dd_theta = (-dd_x*np.cos(theta) + dx*np.sin(theta)*dtheta - np.sin(theta)*(dx*dtheta + g)) / lreturn np.array([dx, dtheta, dd_x, dtheta])# 四阶龙格库塔法函数
def RK4(t_start, t_end, fun, Npoints, init_state, u_list, pos_des, spd_des):t = np.linspace(t_start, t_end, Npoints)dt = t[1] - t[0]state = np.zeros((Npoints, len(init_state)))state[0, :] = init_statee = np.zeros((Npoints, 2))for i in range(Npoints-1):u_list[i] = u_list[i] + 1 * (spd_des[i] - state[i, 2]) # 闭环D型更新率u = u_list[i]e[i, 0] = pos_des[i] - state[i, 0]e[i, 1] = spd_des[i] - state[i, 2]k1 = fun(state[i, :], u)k2 = fun(state[i, :] + 0.5 * dt * k1, u)k3 = fun(state[i, :] + 0.5 * dt * k2, u)k4 = fun(state[i, :] + dt * k3, u)state[i + 1, :] = state[i, :] + (1/6) * dt * (k1 + 2 * k2 + 2 * k3 + k4)return state, u_list, e# 参数设置
m1 = 5
m2 = 1
l = 1
g = 9.8t_start = 0
t_end = 10
Npoints = 10000
t = np.linspace(t_start, t_end, Npoints)# 期望位置和速度
pos_des = np.sin(t) + t
spd_des = np.cos(t) + 1pos_des = t * t + 2 * t
spd_des = 2 * t + 2# 初始状态和控制输入
u_list = [0] * 10000# 创建图形对象
plt.figure(figsize=(12, 12))for i in range(20):# 运行RK4state, u_list, e_buff = RK4(t_start, t_end, dynamics, Npoints, [0, 0, 0, 0], u_list, pos_des, spd_des)# 清除当前图像plt.clf()# 绘制实际位置和期望位置的对比图plt.subplot(3, 1, 1)plt.plot(t, state[:, 0], label='Actual x (position)')plt.plot(t, pos_des, label='Desired x (position)', linestyle='--')plt.xlabel('Time (s)')plt.ylabel('Position')plt.legend()plt.title(f'Iteration {i+1}')# 绘制实际速度和期望速度的对比图plt.subplot(3, 1, 2)plt.plot(t, state[:, 2], label='Actual dx (velocity)')plt.plot(t, spd_des, label='Desired dx (velocity)', linestyle='--')plt.xlabel('Time (s)')plt.ylabel('Velocity')plt.legend()# 绘制控制输入(力)曲线plt.subplot(3, 1, 3)plt.plot(t, u_list, label='Control input (force)')plt.xlabel('Time (s)')plt.ylabel('Force')plt.legend()# 显示图像plt.pause(0.01)# 最后显示图像
plt.show()# 将误差和力存储到CSV文件
data = np.hstack((e_buff, np.array(u_list).reshape(-1, 1)))
df = pd.DataFrame(data, columns=['Position Error', 'Velocity Error', 'Control Input'])
df.to_csv('error_and_force_data.csv', index=False)
5、实物效果
-
这个曲线不是上面仿真小车钟摆的实物测试,而是一个有一定质量的物体yaw轴回转的控制效果,展示的是位置曲线。这个物体受到不小的摩擦力,所以在开始迭代时开始和后来都会有停止不动的情况出现。同时,摩擦力也导致这个物体受到很大的干扰,就像小车钟摆的重物一样。
-
值得一提的是整个实物的算法测试过程非常顺利,在代码完成后,一次测试就成功了。使用的还是闭环D型迭代学习,经过三四次迭代就收敛到期望曲线附近了。这说明迭代学习还是一种很实用的算法。

相关文章:

迭代学习笔记
一、迭代学习定义和分类 1、直观理解 迭代学习一般应用于重复性的场景。比如控制一个单自由度的小车以特定的速度曲线移动到指定位置,整个时间是10s,控制频率是0.01,那么整个控制序列就会有1000个点。这1000个点在10s内依次发出,…...

【安全】系统安全设计规范(DOC完整版)
1.1安全建设原则 1.2 安全管理体系 1.3 安全管理规范 1.4 数据安全保障措施 1.4.1 数据库安全保障 1.4.2 操作系统安全保障 1.4.3 病毒防治 1.5安全保障措施 1.5.1实名认证保障 1.5.2 接口安全保障 1.5.3 加密传输保障 1.5.4终端安全保障 软件资料清单列表部分文档&…...

windows常用命令整理
本文分享一些常用的windows命令。根据功能的不同,大致可分为以下几个方面,一是文件操作命令,二是进程相关命令,三是磁盘相关命令,四是网络相关命令,五是其他命令。 1.文件操作命令 dir:显示当…...

视频处理基础知识1
1、图像基本知识 图像的组成:像素、RGB(每个像素由三个发光二极管组成)、分辨率(横纵向像素的个数乘积) PPI每英寸的像素数 DPI每英寸的点数,有可能一个点有多个像素 PPI>300 就属于视网膜级别,就是很清晰&#…...

Linux退不出vim编辑模式
目录 第一章、问题分析1.1)报错提示 第二章、解决方式 友情提醒: 先看文章目录,大致了解文章知识点结构,点击文章目录可直接跳转到文章指定位置。 第一章、问题分析 1.1)报错提示 报错如下:使用Linux的vi…...

TikTok养号的网络环境及相关代理IP知识
TikTok作为一个流行的短视频分享平台,其用户量非常庞大,很多商家和个人都会使用TikTok来进行引流和推广。由于TikTok的规则和政策限制了每个用户每天发布视频的数量,因此许多用户会使用多个账号来发布更多的视频以提高曝光率。 然而ÿ…...

过程调用和数组的分配访问
系列文章 : 深入理解计算机系统笔记 文章目录 系列文章3.7 过程3.7.1 运行时栈3.7.2 转移控制3.7.3 数据传送3.7.4 栈上的局部存储3.7.5 寄存器中的局部存储空间3.7.6 递归过程 3.8 数组分配和访问3.8.1 基本原则3.8.2 指针运算3.8.3 嵌套的数组3.8.4 定长数组3.8.5 变长数组…...

TeamViewer手机端APP提示:请先验证账户
当你在手机端下载安装了TeamViewerAPP后,需要你先登录个人账号,然后还会要求你验证账户,同时跳转到一个网址中,但是这个网址并没有自动跳转到验证账户的位置。 解决办法: 在手机浏览器中进入下面这个网址:…...

【SpringBoot】分页查询
1. Controller ApiOperation("分页查询")GetMapping("/page")public Result<PageResult> pageResultResult(EmployeePageQueryDTO employeePageQueryDTO) {System.out.println(employeePageQueryDTO.toString());PageResult pageResult employeeSer…...
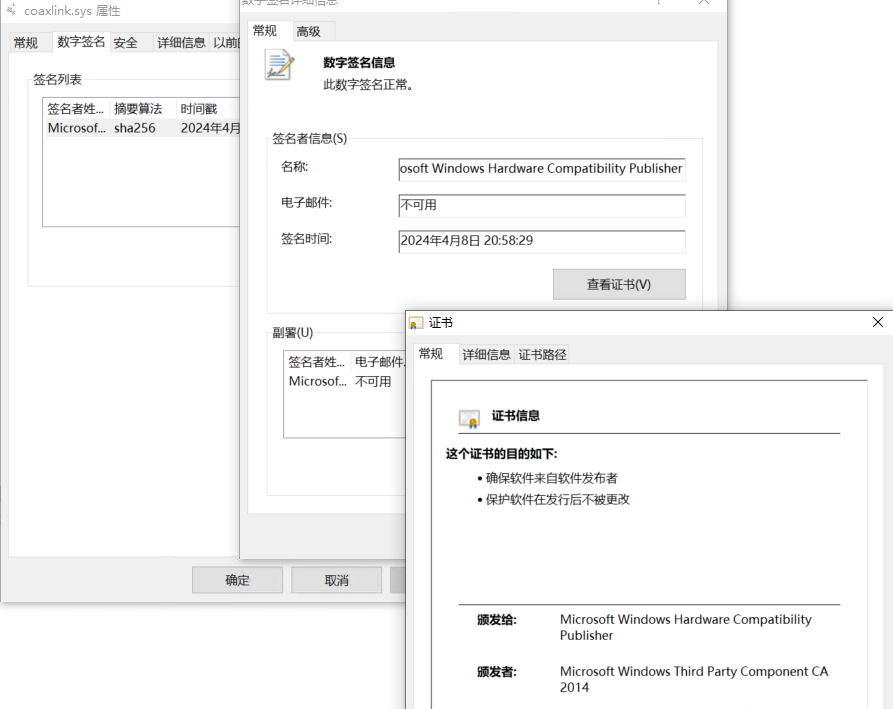
微软CrowdStrike驱动蓝屏以及内核签名
原因 当Windows操作系统遇到严重错误导致系统崩溃时,屏幕显示为蓝色,通常伴有错误代码和信息,这被称为“蓝屏死机”(Blue Screen of Death,简称BSOD) https://www.thepaper.cn/newsDetail_forward_281262…...
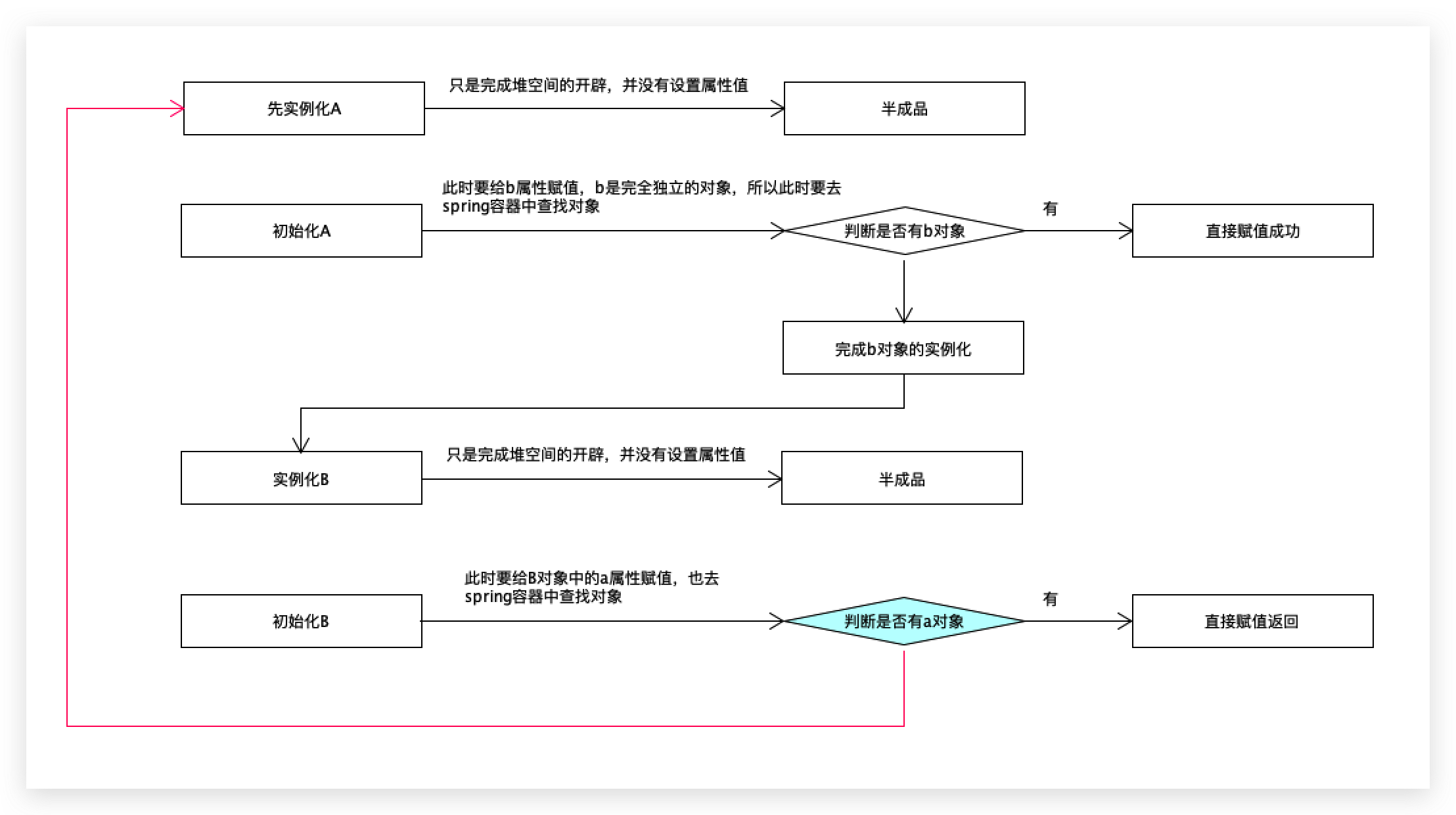
Spring中Bean的循环依赖
目录 定义: 循环依赖的后果: 一:三级缓存 1、大概的思路: 注意: 2、执行过程: A半完成: B完成: A完成: 注: 二:Lazy 定义: …...

Java二十三种设计模式-代理模式模式(8/23)
代理模式:为对象访问提供灵活的控制 引言 代理模式(Proxy Pattern)是一种结构型设计模式,它为其他对象提供一个代替或占位符,以控制对它的访问。 基础知识,java设计模式总体来说设计模式分为三大类&#…...

Windows 11 家庭中文版 安装 VMWare 报 安装程序检测到主机启用了Hyper-V或Device
1、问题 我的操作系统信息如下: 我在安装 VMWare 的时候,报: 因为我之前安装了 docker 桌面版,所以才报这个提示。 安装程序检测到主机启用了 Hyper-v或 Device/credential Guard。要在启用了Hyper-或 Device/Credential Guard …...

机械学习—零基础学习日志(高数09——函数图形)
零基础为了学人工智能,真的开始复习高数 函数图像,开始新的学习! 幂函数 利用函数的性质,以幂函数为例,因为单调性相同,利用图中的2和3公式,求最值问题,可以直接将式子进行简化。这…...

java迭代集合出现并发修改异常(ConcurrentModificationException)的原因以及解决方案
java迭代集合出现并发修改异常(ConcurrentModificationException)的原因以及解决方案 一. 什么时候会出现并发修改异常? 这里先看需求 : 定义一个集合,存储 唐僧,孙悟空,猪八戒,沙僧,遍历集合,如果遍历到猪八戒,往集合中添加一个白龙马 很显然要求我们先创建一个集合并进行…...

BGP选路之Local Preference
原理概述 当一台BGP路由器中存在多条去往同一目标网络的BGP路由时,BGP协议会对这些BGP路由的属性进行比较,以确定去往该目标网络的最优BGP路由。BGP首先比较的是路由信息的首选值(PrefVal),如果 PrefVal相同,就会比较本…...

WEB渗透信息收集篇--IP和端口信息
WEB渗透信息收集篇--域名信息-CSDN博客 WEB渗透信息收集篇--网站架构和指纹识别-CSDN博客 WEB渗透信息收集篇--人员信息-CSDN博客 WEB渗透信息收集篇--其他信息-CSDN博客 一、ASN ASN Tool - MxToolBox ASN通常指的是"自…...

国内微短剧系统平台抖音微信付费小程序app开发源代码交付
微短剧作为当下热门的内容,结合抖音平台的广泛用户基础,开发微短剧付费小程序APP具有显著的市场潜力,用户对于短剧内容的需求旺盛,特别是在言情、总裁、赘婿等热门题材方面,接下来给大家普及一下微短剧小程序系统。 顺…...

Java语言程序设计基础篇_编程练习题**15.19 (游戏:手眼协调)
**15.19 (游戏:手眼协调) 请编写一个程序,显示一个半径为10像素的实心圆,该圆放置在面板上的随机位置,并填充随机的顔色,如图15-29b所示。单击这个圆时,它会消失,然后在另一个随机的位置显示新的随机颜色的…...

学习记录day16—— 数据结构 双向链表 循环链表
双向链表 1、概念 1)就是从任意一个节点既能存储其前驱节点,又能存储后继节点 2)结构体中增加一个指向前驱节点的指针 //定义数据类型 typedef int datatype;//定义节点类型 typedef struct Node {union {int len;datatype data;};struct Node *prio; …...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
