力扣第二十九题——两数相除
内容介绍
给你两个整数,被除数
dividend和除数divisor。将两数相除,要求 不使用 乘法、除法和取余运算。整数除法应该向零截断,也就是截去(
truncate)其小数部分。例如,8.345将被截断为8,-2.7335将被截断至-2。返回被除数
dividend除以除数divisor得到的 商 。注意:假设我们的环境只能存储 32 位 有符号整数,其数值范围是
[−231, 231 − 1]。本题中,如果商 严格大于231 − 1,则返回231 − 1;如果商 严格小于-231,则返回-231。示例 1:
输入: dividend = 10, divisor = 3 输出: 3 解释: 10/3 = 3.33333.. ,向零截断后得到 3 。示例 2:
输入: dividend = 7, divisor = -3 输出: -2 解释: 7/-3 = -2.33333.. ,向零截断后得到 -2 。提示:
-231 <= dividend, divisor <= 231 - 1divisor != 0
完整代码
class Solution {public int divide(int dividend, int divisor) {if (dividend == Integer.MIN_VALUE) {if (divisor == 1) {return Integer.MIN_VALUE;}if (divisor == -1) {return Integer.MAX_VALUE;}}if (divisor == Integer.MIN_VALUE) {return dividend == Integer.MIN_VALUE ? 1 : 0;}if (dividend == 0) {return 0;}boolean rev = false;if (dividend > 0) {dividend = -dividend;rev = !rev;}if (divisor > 0) {divisor = -divisor;rev = !rev;}int left = 1, right = Integer.MAX_VALUE, ans = 0;while (left <= right) {int mid = left + ((right - left) >> 1);boolean check = quickAdd(divisor, mid, dividend);if (check) {ans = mid;if (mid == Integer.MAX_VALUE) {break;}left = mid + 1;} else {right = mid - 1;}}return rev ? -ans : ans;}public boolean quickAdd(int y, int z, int x) {int result = 0, add = y;while (z != 0) {if ((z & 1) != 0) {if (result < x - add) {return false;}result += add;}if (z != 1) {if (add < x - add) {return false;}add += add;}z >>= 1;}return true;}
}思路详解
整体思路
该代码实现了一个整数除法功能,主要解决以下问题:
- 处理特殊边界情况,如被除数或除数为整数最小值。
- 处理除数为0的情况。
- 通过二分查找确定商的大小。
- 使用快速乘法判断二分查找中的中间值是否满足条件。
详细步骤
-
处理特殊边界情况
- 当被除数为
Integer.MIN_VALUE时,需要单独处理除数为1和-1的情况,因为直接计算会导致溢出。 - 当除数为
Integer.MIN_VALUE时,只有当被除数也是Integer.MIN_VALUE时,商为1,否则为0。
- 当被除数为
-
处理除数为0的情况
- 当被除数为0时,直接返回0。
-
统一处理负数
- 将被除数和除数都转换为负数,这样只需考虑一种情况。同时记录转换次数,最后根据转换次数确定返回值的正负。
-
二分查找确定商的大小
- 初始化左边界为1,右边界为
Integer.MAX_VALUE。 - 在二分查找过程中,计算中间值
mid,并使用快速乘法判断mid * divisor是否大于等于dividend。 - 如果满足条件,更新答案
ans,并将左边界更新为mid + 1;否则,将右边界更新为mid - 1。
- 初始化左边界为1,右边界为
-
快速乘法
- 由于不能使用除法,使用快速乘法来判断
mid * divisor是否大于等于dividend。 - 通过位运算和加法模拟乘法操作,同时避免溢出。
- 由于不能使用除法,使用快速乘法来判断
代码注释说明
rev:记录被除数和除数转换为负数的次数,用于最后确定返回值的正负。quickAdd:快速乘法函数,用于判断y * z是否大于等于x。left、right、ans:二分查找的左边界、右边界和当前答案。mid:二分查找的中间值。check:用于判断mid * divisor是否大于等于dividend。
知识点精炼
特殊情况处理
- 整数最小值:处理
Integer.MIN_VALUE作为被除数或除数的情况,防止溢出。 - 除数为0:明确除数为0时,结果为0。
负数统一处理
- 符号转换:将被除数和除数统一转换为负数,简化问题处理。
- 符号记录:使用布尔变量记录被除数和除数的符号转换次数,以确定最终结果的符号。
二分查找
- 查找范围:初始化左边界为1,右边界为
Integer.MAX_VALUE。 - 中间值计算:使用位运算计算中间值,避免溢出。
- 条件判断:通过快速乘法判断中间值是否满足条件。
快速乘法
- 位运算:利用位运算模拟乘法操作,避免直接使用乘法导致溢出。
- 加法替代:通过加法累加结果,判断是否满足条件。
防溢出
- 边界检查:在计算过程中,确保不发生溢出。
- 无除法:全程不使用除法操作,避免因除法导致的精度问题。
相关文章:

力扣第二十九题——两数相除
内容介绍 给你两个整数,被除数 dividend 和除数 divisor。将两数相除,要求 不使用 乘法、除法和取余运算。 整数除法应该向零截断,也就是截去(truncate)其小数部分。例如,8.345 将被截断为 8 ,-…...

解析三款热门的文献翻译工具:优势与使用指南
今儿咱们来聊聊那些让咱们头疼又不得不面对的事儿——文献翻译。在浩瀚的学术海洋里遨游时,遇到外文文献那是家常便饭,但语言障碍就像海上的迷雾,一不小心就能让你偏离航向。别担心,我这不就带着几款亲测好用的文献翻译神器来了嘛…...

git 过滤LFS文件下载
git config --global filter.lfs.smudge "git-lfs smudge --skip -- %f" git config --global filter.lfs.process "git-lfs filter-process --skip" 恢复下载 git config --global filter.lfs.smudge "git-lfs smudge -- %f" git config --g…...

内存泄漏详解
文章目录 什么是内存泄漏内存泄漏的原因排查及解决内存泄漏避免内存泄漏及时释放资源设置合理的变量作用域及时清理不需要的对象避免无限增长避免内部类持有外部类引用使用弱引用 什么是内存泄漏 内存泄漏是指不使用的对象持续占有内存使得内存得不到释放,从而造成…...

多角度解析高防CDN防御DDOS及CC攻击
网络攻击的形式也日益多样化,其中DDoS(分布式拒绝服务)和CC(Challenge Collapsar)攻击尤为突出,给网站和企业带来了巨大的安全威胁。高防CDN(Content Delivery Network)作为一种专业…...

(7) cmake 编译C++程序(二)
文章目录 概要整体代码结构整体代码小结 概要 在ubuntu下,通过cmake编译一个稍微复杂的管理程序 整体代码结构 整体代码 boss.cpp #include "boss.h"Boss::Boss(int id, string name, int dId) {this->Id id;this->Name name;this->DeptId …...

C语言系统调用linux文件系统
在C语言中,open、write和read函数是系统调用(system calls),它们直接由操作系统提供,用于底层的文件操作。这些函数是UNIX和类UNIX系统(如Linux)中的标准接口,不同于C标准库中的文件…...

LeetCode142 环形链表 II
前言 题目: 142. 环形链表 II 文档: 代码随想录——环形链表 II 编程语言: C 解题状态: 思路错误,链表不允许被修改 思路 两步走,第一步,判断有没有环,第二步,判断入环口…...

逆向案例二十八——某高考志愿网异步请求头参数加密,以及webpack
网址:aHR0cDovL3d3dy54aW5nYW9rYW90Yi5jb20vY29sbGVnZXMvc2VhcmNo 抓包分析,发现请求头有参数u-sign是加密的,载荷没有进行加密,直接跟栈分析。 进入第二个栈,打上断点,分析有没有加密位置。 可以看到参数…...

WebKit的文本装饰艺术:CSS Text Decoration全解析
WebKit的文本装饰艺术:CSS Text Decoration全解析 CSS文本装饰(Text Decoration)是一组用于美化和增强网页文本表现的属性,它们可以为文本添加下划线、上划线、线删除和强调标记等效果。WebKit作为许多现代浏览器的渲染引擎&…...

【linux】Shell脚本三剑客之sed命令的详细用法攻略
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,阿里云开发者社区专家博主,CSDN全栈领域优质创作者,掘金优秀博主,51CTO博客专家等。 🏆《博客》:Python全…...

解析class字节码文件获取魔数和版本号
写在前面 本文看下如何获取class字节码文件的魔数和版本号信息。 1:正文 需要对class字节码的结构有一定的了解,可以参考这篇文章 。 直接看代码: package org.example;import java.math.BigInteger;public class TTTT {//取部分字节码&…...

技术文档总结----思维导图
性能调优| ProcessOn免费在线作图,在线流程图,在线思维导图 mysql| ProcessOn免费在线作图,在线流程图,在线思维导图 kafka| ProcessOn免费在线作图,在线流程图,在线思维导图 mybatis缓存| ProcessOn免费在线作图,在线流程图,在线思维导图 java锁| ProcessOn免费在线作图,在…...
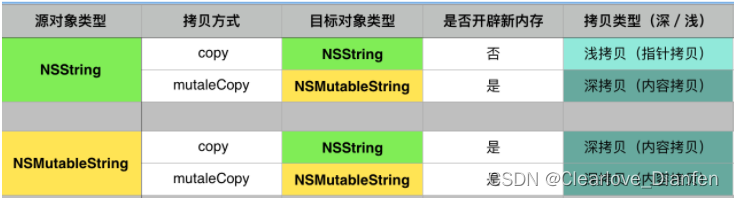
【iOS】—— retain\release实现原理和属性关键字
【iOS】—— retain\release实现原理和属性关键字 1. retain\reelase实现原理1.1 retain实现原理1.2 release实现原理 2. 属性关键字2.1 属性关键字的分类2.2 内存管理关键字2.2.1 weak2.2.2 assgin2.3.3 strong和copy 2.4 线程安全的关键字2.5 修饰变量的关键字2.5.1常量const…...

这一文,关于Java泛型的点点滴滴 一
作为一个 Java 程序员,用到泛型最多的,我估计应该就是这一行代码: List<String> list new ArrayList<>();这也是所有 Java 程序员的泛型之路开始的地方啊。 不过本文讲泛型,先不从这里开始讲,而是再往前…...
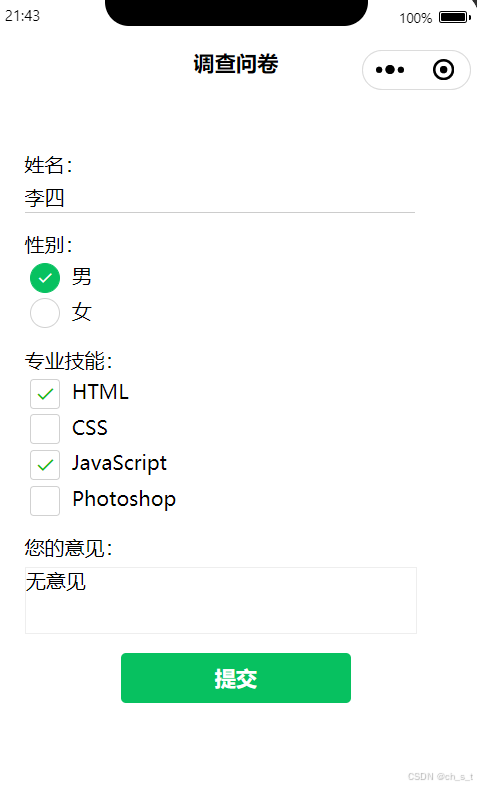
微信小程序之调查问卷
一、设计思路 1、界面 调查问卷又称调查表,是以问题的形式系统地记载调查内容的一种形式。微信小程序制作的调查问卷,可以在短时间内快速收集反馈信息。具体效果如下所示: 2、思路 此调查问卷采用服务器客户端的方式进行设计,服…...

基于Qt的视频剪辑
在Qt中进行视频剪辑可以通过多种方式实现,但通常需要使用一些额外的库来处理视频数据。以下是一些常见的方法和步骤: 使用FFmpeg FFmpeg是一个非常强大的多媒体框架,可以用来处理视频和音频数据。你可以使用FFmpeg的命令行工具或者其库来实现…...

electron 网页TodoList工具打包成win桌面应用exe
参考: electron安装(支持win、mac、linux桌面应用) https://blog.csdn.net/weixin_42357472/article/details/140643624 TodoList工具 https://blog.csdn.net/weixin_42357472/article/details/140618446 electron打包过程: 要将…...

数据结构之判断二叉树是否为搜索树(C/C++实现)
文章目录 判断二叉树是否为搜索树方法一:递归法方法二:中序遍历法总结 二叉树是一种非常常见的数据结构,它在计算机科学中有着广泛的应用。二叉搜索树(Binary Search Tree,简称BST)是二叉树的一种特殊形式&…...

golang长连接的误用
误用一:忘记读取响应的body 由于忘记读取响应的body导致创建大量处于TIME_WAIT状态的连接(同时产生大量处于transport.go的readLoop和writeLoop的协程) 在linux下运行下面的代码: package mainimport ("fmt""html"&qu…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
