数据结构之判断二叉树是否为搜索树(C/C++实现)
文章目录
- 判断二叉树是否为搜索树
- 方法一:递归法
- 方法二:中序遍历法
- 总结

二叉树是一种非常常见的数据结构,它在计算机科学中有着广泛的应用。二叉搜索树(Binary Search Tree,简称BST)是二叉树的一种特殊形式,它具有以下性质:对于树中的任意一个节点,其左子树中的所有节点的值都小于该节点的值,其右子树中的所有节点的值都大于该节点的值。本文将详细介绍如何判断一个二叉树是否为搜索树,并提供C和C++的实现示例。
判断二叉树是否为搜索树
思路
判断一个二叉树是否为搜索树,可以通过以下两种方法:
- 递归法
- 中序遍历法
下面分别对这两种方法进行详细讲解。
方法一:递归法
递归法的核心思想是:对于树中的每个节点,检查其左子树的最大值是否小于当前节点的值,以及其右子树的最小值是否大于当前节点的值。
- 如果树为空,则它是二叉搜索树。
- 对于当前节点,递归地检查其左子树的最大值是否小于当前节点的值,同时检查其右子树的最小值是否大于当前节点的值。
- 如果上述两个条件均满足,则递归地检查左子树和右子树是否都是二叉搜索树。
C语言实现
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>typedef struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;
} TreeNode;// 判断二叉树是否为搜索树
int isBSTUtil(struct TreeNode* node, int min, int max) {if (node == NULL) return 1;if (node->val < min || node->val > max) return 0;return isBSTUtil(node->left, min, node->val - 1) && isBSTUtil(node->right, node->val + 1, max);
}int isBST(TreeNode* root) {return isBSTUtil(root, INT_MIN, INT_MAX);
}// 创建新节点
TreeNode* newNode(int val) {TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));node->val = val;node->left = node->right = NULL;return node;
}int main() {TreeNode *root = newNode(4);root->left = newNode(2);root->right = newNode(5);root->left->left = newNode(1);root->left->right = newNode(3);if (isBST(root))printf("是搜索树\n");elseprintf("不是搜索树\n");return 0;
}
C++实现
#include <iostream>
#include <climits>using namespace std;struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};// 判断二叉树是否为搜索树
bool isBSTUtil(TreeNode* node, int min, int max) {if (node == NULL) return true;if (node->val < min || node->val > max) return false;return isBSTUtil(node->left, min, node->val - 1) && isBSTUtil(node->right, node->val + 1, max);
}bool isBST(TreeNode* root) {return isBSTUtil(root, INT_MIN, INT_MAX);
}int main() {TreeNode *root = new TreeNode(4);root->left = new TreeNode(2);root->right = new TreeNode(5);root->left->left = new TreeNode(1);root->left->right = new TreeNode(3);if (isBST(root))cout << "是搜索树" << endl;elsecout << "不是搜索树" << endl;return 0;
}
方法二:中序遍历法
中序遍历法的基本思想是:对二叉树进行中序遍历,遍历过程中检查当前节点的值是否大于前一个节点的值。如果是,则为搜索树;否则,不是搜索树。
C语言实现
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>typedef struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;
} TreeNode;// 全局变量,用于记录前一个节点的值
int prev = INT_MIN;bool isBSTInorder(TreeNode* root) {if (root != NULL) {// 遍历左子树if (!isBSTInorder(root->left))return false;// 检查当前节点的值是否大于前一个节点的值if (root->val <= prev)return false;prev = root->val;// 遍历右子树return isBSTInorder(root->right);}return true;
}// 创建新节点
TreeNode* newNode(int val) {TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));node->val = val;node->left = node->right = NULL;return node;
}int main() {TreeNode *root = newNode(4);root->left = newNode(2);root->right = newNode(5);root->left->left = newNode(1);root->left->right = newNode(3);if (isBSTInorder(root))printf("是搜索树\n");elseprintf("不是搜索树\n");return 0;
}C++实现
#include <iostream>
#include <climits>using namespace std;struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};// 全局变量,用于记录前一个节点的值
int prev = INT_MIN;bool isBSTInorder(TreeNode* root) {if (root == nullptr) return true;if (!isBSTInorder(root->left))return false;if (root->val <= prev)return false;prev = root->val;return isBSTInorder(root->right);
}int main() {TreeNode *root = new TreeNode(4);root->left = new TreeNode(2);root->right = new TreeNode(5);root->left->left = new TreeNode(1);root->left->right = new TreeNode(3);if (isBSTInorder(root))cout << "是搜索树" << endl;elsecout << "不是搜索树" << endl;return 0;
}
总结
本文详细介绍了如何判断一个二叉树是否为搜索树,包括递归法和中序遍历法两种实现方式。递归法通过比较节点与其子树的关系来判断,而中序遍历法则通过比较中序遍历的节点值来判断。两种方法各有优劣,可以根据实际需求选择合适的方法
相关文章:

数据结构之判断二叉树是否为搜索树(C/C++实现)
文章目录 判断二叉树是否为搜索树方法一:递归法方法二:中序遍历法总结 二叉树是一种非常常见的数据结构,它在计算机科学中有着广泛的应用。二叉搜索树(Binary Search Tree,简称BST)是二叉树的一种特殊形式&…...

golang长连接的误用
误用一:忘记读取响应的body 由于忘记读取响应的body导致创建大量处于TIME_WAIT状态的连接(同时产生大量处于transport.go的readLoop和writeLoop的协程) 在linux下运行下面的代码: package mainimport ("fmt""html"&qu…...

Springboot @Validate @Valid 基于复杂嵌套对象的参数校验示例
Springboot Validate Valid 基于复杂嵌套对象的参数校验示例 复杂对象 Data public class Object1 {Length(max 50,message "长度不能超过50位字符")NotBlank(message "名称不能为空")private String name;NotNull(message "不能为空")pri…...

算力共享下的,分级路由转发报文协议与通告
目录 网络双 SLA 约束 一、双SLA约束的定义与背景 二、双SLA约束的应用场景 三、双SLA约束的管理与实施 四、双SLA约束的优势与挑战 算力共享下的,分级路由转发报文协议与通告 基础设施即服务(IaaS)类 型算力资源 函数即服务(FaaS)类型算力服务 软件即服务(SaaS…...

滚动数组详解
滚动数组详解 何为滚动数组?滚动数组是如何优化空间的?交替滚动例题:来自某某轮廓线DP的题目 自我滚动(~~不如交替~~ 完结!!! ( 宇宙免责任书:我用的是C) 何为滚动数组? 什么是滚动…...

C 语言动态链表
线性结构->顺序存储->动态链表 一、理论部分 从起源中理解事物,就是从本质上理解事物。 -杜勒鲁奇 动态链表是通过结点(Node)的集合来非连续地存储数据,结点之间通过指针相互连接。 动态链表本身就是一种动态分配内存的…...

【Leetcode】二十、记忆化搜索:零钱兑换
文章目录 1、记忆化搜索2、leetcode509:斐波那契数列3、leetcode322:零钱兑换 1、记忆化搜索 也叫备忘录,即把已经计算过的结果存下来,下次再遇到,就直接取,不用重新计算。目的是以减少重复计算。 以前面提…...

json数据格式 继续学习
1.定义 轻量级的数据交互格式,可以按照json数据格式去组织和封装数据。 本质是一个带有特定格式的字符串。 2.功能 负责不同编程语言中的数据传递和交互。 3.json数据格式转化 """ 演示json数据和python字典之间的转换 """ impor…...

gradle 构建项目添加版本信息
gradle 构建项目添加版本信息,打包使用 spring boot 的打包插件 build.gradle 配置文件 bootJar {manifest {attributes(Project-Name: project.name,Project-Version: project.version,"project-Vendor": "XXX Corp","Built-By": &…...

vue3 学习笔记17 -- 基于el-menu封装菜单
vue3 学习笔记17 – 基于el-menu封装菜单 前提条件:组件创建完成 配置路由 // src/router/index.ts import { createRouter, createWebHashHistory } from vue-router import type { RouteRecordRaw } from vue-router export const Layout () > import(/lay…...
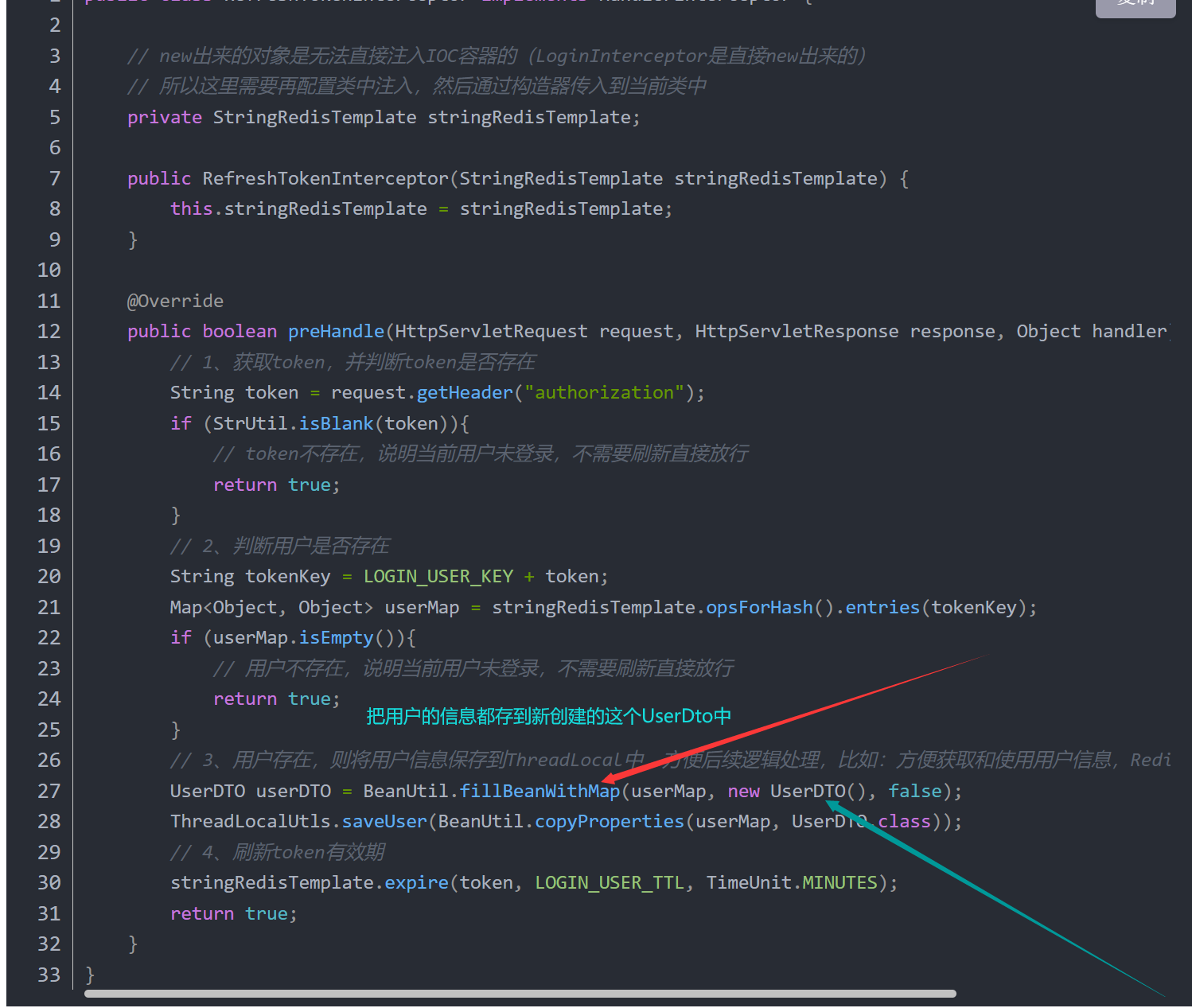
使用 Redis 实现验证码、token 的存储,用自定义拦截器完成用户认证、并使用双重拦截器解决 token 刷新的问题
可以看一下我以前做过的笔记:黑马点评 短信登录部分 基于session实现登录流程 1.发送验证码 用户在提交手机号后,会校验手机号是否合法,如果不合法,则要求用户重新输入手机号 如果手机号合法,后台此时生成对应的验…...
C语言)
反转链表 - 力扣(LeetCode)C语言
206. 反转链表 - 力扣(LeetCode)( 点击前面链接即可查看题目) /*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/ struct ListNode* reverseList(struct ListNode* head) {if(head NULL)…...

【Linux】进程间通信(1):进程通信概念与匿名管道
人与人之间是如何通信的?举个简单的例子,假如我是月老,我要为素不相识的但又渴望爱情的男女两方牵红线。我需要收集男方的信息告诉女方,收集女方的信息告诉男方,然后由男女双方来决定是否继续。对于他们而言࿰…...

Spring从入门到精通 01
文章目录 1. 依赖注入 (Dependency Injection, DI)2. 面向切面编程 (Aspect-Oriented Programming, AOP)3. 事务管理4. 简化 JDBC 开发5. 集成各种框架和技术6. 模块化和扩展性:主要的 Spring 模块:Core Container:AOP 模块:Data …...

C语言经典习题25
冒泡排序 对一维数组进行升序排序,然后在数组中输入20个数,将排序后的结果打印输出。 #include<stdio.h> #define N 20 int main() {int a[N];int i;for(i0;i<N;i) //初始化数组的数 {scanf("%d",&a);}for(i0;…...

2-47 基于matlab的时域有限差分法(FDTD法)拉夫等效原理进行时谐场外推
基于matlab的时域有限差分法(FDTD法)拉夫等效原理进行时谐场外推。外推边界距离吸收边界的距离、电磁场循环、傅立叶变换提起幅值和相位、各远区剖分点电场、方向系数计算等操作,得出可视化结果。程序已调通,可直接运行。 2-47 时域有限差分法(FDTD法) 拉…...

JupyterNotebook快捷键 自用
COMMAND MODE —————————————————————————————— Up Down cells的上下选择 A B 在上/下方插入cell C V X 复制/粘贴/剪切cell 双击D 删除所选cell Z 恢复被删除的cell 双击I Interrupt中断内核 Shift Enter 运行cell并选择下方 EDIT MODE ———…...

【我的OpenGL学习进阶之旅】讲一讲GL_TEXTURE_2D和GL_TEXTURE_EXTERNAL_OES的区别
在使用OpenGL ES进行图形图像开发时,我们常使用GL_TEXTURE_2D纹理类型,它提供了对标准2D图像的处理能力。这种纹理类型适用于大多数场景,可以用于展示静态贴图、渲染2D图形和进行图像处理等操作。 另外,有时我们需要从Camera或外部视频源读取数据帧并进行处理。这时,我们…...

Makefile 如何将生成的 .o 文件放到指定文件夹
研究了不少文章,我行通了一个,但是也不全,目前只能适用当前文件夹,如果源文件有子文件夹处理不了,还得继续研究。很多人说编译完把O文件移动走或者直接删掉。我想说的是不符合我的要求,移走或者删除O文件&a…...

聊一聊知识图谱结合RAG
因为最近在做一些关于提高公司内部使用的聊天机器人的回答准确率,并且最近微软官方也是开源了一下graphrag的源码,所以想聊一聊这个知识图谱结合rag。 rag在利用私有数据增强大模型回答的领域是一种比较典型的技术,也就是我们提出问题的时候&…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...
