算力共享下的,分级路由转发报文协议与通告
目录
网络双 SLA 约束
一、双SLA约束的定义与背景
二、双SLA约束的应用场景
三、双SLA约束的管理与实施
四、双SLA约束的优势与挑战
算力共享下的,分级路由转发报文协议与通告
基础设施即服务(IaaS)类 型算力资源
函数即服务(FaaS)类型算力服务
软件即服务(SaaS)类型算力服务
算力资源和服务的度量和标识
基于 BGP 的分级路由机制
通告可有两种
基于 BGP 的地址路由和算力服务路由的两级路由表机制
新型算力路由协议
基于 SRv6 的算力网络增强转发面技术
BRAS
执行 IP 拓扑地址封装封装方案:
算力服务标识的封装包括两种方案:
解释(2)算力服务标识封装:
封装机制
技术优势与应用场景
IP ,L4传输层,overlay
简单举例说明
overlay层的作用
常见的overlay技术
片段识别(SID,Segment Identifier)
网络双 SLA 约束
网络双SLA约束是指在网络服务中,存在两个或多个服务级别协议(SLA)同时对服务质量进行约束的情况。SLA是服务提供商与客户之间具有法律约束力的协议,它规定了服务提供商必须达到的服务质量标准。在网络环境中,特别是在复杂的网络架构和多样化的服务需求下,可能会引入双SLA或多重SLA约束,以确保不同层面或不同服务组件的性能和可靠性。
关于网络双SLA约束,可以从以下几个方面进行理解和分析:
一、双SLA约束的定义与背景
- 定义:双SLA约束指的是在同一网络环境中,存在两个独立的SLA,它们分别对不同的服务组件或性能指标进行约束。这些SLA可能由不同的服务提供商与客户之间签订,也可能在同一个服务提供商内部不同部门或团队之间制定。
- 背景:随着网络技术的不断发展和服务需求的日益复杂化
相关文章:

算力共享下的,分级路由转发报文协议与通告
目录 网络双 SLA 约束 一、双SLA约束的定义与背景 二、双SLA约束的应用场景 三、双SLA约束的管理与实施 四、双SLA约束的优势与挑战 算力共享下的,分级路由转发报文协议与通告 基础设施即服务(IaaS)类 型算力资源 函数即服务(FaaS)类型算力服务 软件即服务(SaaS…...

滚动数组详解
滚动数组详解 何为滚动数组?滚动数组是如何优化空间的?交替滚动例题:来自某某轮廓线DP的题目 自我滚动(~~不如交替~~ 完结!!! ( 宇宙免责任书:我用的是C) 何为滚动数组? 什么是滚动…...

C 语言动态链表
线性结构->顺序存储->动态链表 一、理论部分 从起源中理解事物,就是从本质上理解事物。 -杜勒鲁奇 动态链表是通过结点(Node)的集合来非连续地存储数据,结点之间通过指针相互连接。 动态链表本身就是一种动态分配内存的…...

【Leetcode】二十、记忆化搜索:零钱兑换
文章目录 1、记忆化搜索2、leetcode509:斐波那契数列3、leetcode322:零钱兑换 1、记忆化搜索 也叫备忘录,即把已经计算过的结果存下来,下次再遇到,就直接取,不用重新计算。目的是以减少重复计算。 以前面提…...

json数据格式 继续学习
1.定义 轻量级的数据交互格式,可以按照json数据格式去组织和封装数据。 本质是一个带有特定格式的字符串。 2.功能 负责不同编程语言中的数据传递和交互。 3.json数据格式转化 """ 演示json数据和python字典之间的转换 """ impor…...

gradle 构建项目添加版本信息
gradle 构建项目添加版本信息,打包使用 spring boot 的打包插件 build.gradle 配置文件 bootJar {manifest {attributes(Project-Name: project.name,Project-Version: project.version,"project-Vendor": "XXX Corp","Built-By": &…...

vue3 学习笔记17 -- 基于el-menu封装菜单
vue3 学习笔记17 – 基于el-menu封装菜单 前提条件:组件创建完成 配置路由 // src/router/index.ts import { createRouter, createWebHashHistory } from vue-router import type { RouteRecordRaw } from vue-router export const Layout () > import(/lay…...
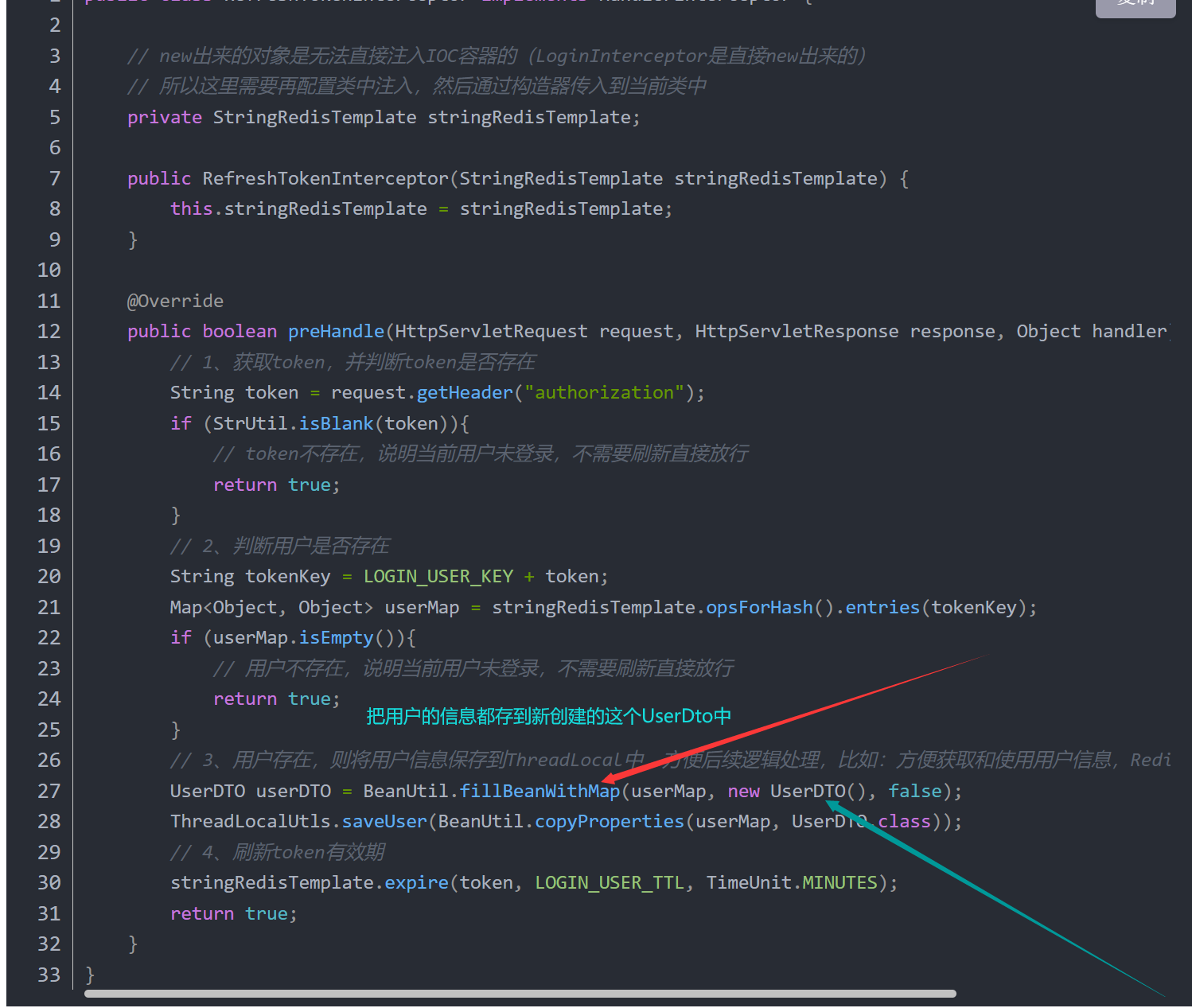
使用 Redis 实现验证码、token 的存储,用自定义拦截器完成用户认证、并使用双重拦截器解决 token 刷新的问题
可以看一下我以前做过的笔记:黑马点评 短信登录部分 基于session实现登录流程 1.发送验证码 用户在提交手机号后,会校验手机号是否合法,如果不合法,则要求用户重新输入手机号 如果手机号合法,后台此时生成对应的验…...
C语言)
反转链表 - 力扣(LeetCode)C语言
206. 反转链表 - 力扣(LeetCode)( 点击前面链接即可查看题目) /*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/ struct ListNode* reverseList(struct ListNode* head) {if(head NULL)…...

【Linux】进程间通信(1):进程通信概念与匿名管道
人与人之间是如何通信的?举个简单的例子,假如我是月老,我要为素不相识的但又渴望爱情的男女两方牵红线。我需要收集男方的信息告诉女方,收集女方的信息告诉男方,然后由男女双方来决定是否继续。对于他们而言࿰…...

Spring从入门到精通 01
文章目录 1. 依赖注入 (Dependency Injection, DI)2. 面向切面编程 (Aspect-Oriented Programming, AOP)3. 事务管理4. 简化 JDBC 开发5. 集成各种框架和技术6. 模块化和扩展性:主要的 Spring 模块:Core Container:AOP 模块:Data …...

C语言经典习题25
冒泡排序 对一维数组进行升序排序,然后在数组中输入20个数,将排序后的结果打印输出。 #include<stdio.h> #define N 20 int main() {int a[N];int i;for(i0;i<N;i) //初始化数组的数 {scanf("%d",&a);}for(i0;…...

2-47 基于matlab的时域有限差分法(FDTD法)拉夫等效原理进行时谐场外推
基于matlab的时域有限差分法(FDTD法)拉夫等效原理进行时谐场外推。外推边界距离吸收边界的距离、电磁场循环、傅立叶变换提起幅值和相位、各远区剖分点电场、方向系数计算等操作,得出可视化结果。程序已调通,可直接运行。 2-47 时域有限差分法(FDTD法) 拉…...

JupyterNotebook快捷键 自用
COMMAND MODE —————————————————————————————— Up Down cells的上下选择 A B 在上/下方插入cell C V X 复制/粘贴/剪切cell 双击D 删除所选cell Z 恢复被删除的cell 双击I Interrupt中断内核 Shift Enter 运行cell并选择下方 EDIT MODE ———…...

【我的OpenGL学习进阶之旅】讲一讲GL_TEXTURE_2D和GL_TEXTURE_EXTERNAL_OES的区别
在使用OpenGL ES进行图形图像开发时,我们常使用GL_TEXTURE_2D纹理类型,它提供了对标准2D图像的处理能力。这种纹理类型适用于大多数场景,可以用于展示静态贴图、渲染2D图形和进行图像处理等操作。 另外,有时我们需要从Camera或外部视频源读取数据帧并进行处理。这时,我们…...

Makefile 如何将生成的 .o 文件放到指定文件夹
研究了不少文章,我行通了一个,但是也不全,目前只能适用当前文件夹,如果源文件有子文件夹处理不了,还得继续研究。很多人说编译完把O文件移动走或者直接删掉。我想说的是不符合我的要求,移走或者删除O文件&a…...

聊一聊知识图谱结合RAG
因为最近在做一些关于提高公司内部使用的聊天机器人的回答准确率,并且最近微软官方也是开源了一下graphrag的源码,所以想聊一聊这个知识图谱结合rag。 rag在利用私有数据增强大模型回答的领域是一种比较典型的技术,也就是我们提出问题的时候&…...
)
Java面试锦集 之 一、Java基础(1)
一、Java基础(1) 1.final 关键字的作用? 修饰变量: 一旦被赋值,就不能再被修改,保证了变量值的稳定性。 例: final int NUMBER 10; //之后就不能再改变 NUMBER 的值了。修饰方法:…...

【leetcode】排列序列
给出集合 [1,2,3,...,n],其所有元素共有 n! 种排列。 按大小顺序列出所有排列情况,并一一标记,当 n 3 时, 所有排列如下: "123""132""213""231""312""321" 给定…...

【Cesium开发实战】视频融合功能的实现,可自定义位置和视频路径
Cesium有很多很强大的功能,可以在地球上实现很多炫酷的3D效果。今天给大家分享一个视频融合功能。 1.话不多说,先展示 视频融合 2.设计思路 点击绘制开始在地图上绘制视频融合的点位,形成视频播放的区域,双击弹框输入名称和要播放视频的路径,即可对应区域播放对应视频,…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
