滚动数组详解
滚动数组详解
- 何为滚动数组?
- 滚动数组是如何优化空间的?
- 交替滚动
- 例题:来自某某轮廓线DP的题目
- 自我滚动(~~不如交替~~
- 完结!!!
(
何为滚动数组?
什么是滚动数组?是会唱跳
rap的数组吗?其实滚动数组就是它名字的意思,一直在滚动的数组。更形容的说就像一个滚轮,在一个状态轴向前后滚动。那么滚轮大家都知道,它是一个动态的东西,那么放到代码中,那其实就是一个数组,像一个滚轮一样,不断的向前递进,但是递进的过程中,并不关心我们的状态,只注重结果,换句话说,这个数组只保存结果。
当然,滚动数组只是一种优化手段,通常用来优化我们的DP的空间,偶尔下降点时间复杂度。
滚动数组是如何优化空间的?
上文中提到,滚动数组其实就是一个在动态滚动的数组,它会在滚动的时候,将浪费也就是可以省的空间给省下来。举个例子, d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − 1 ] ] + a [ i ] dp[i][j] = max(dp[i-1][j], dp[i-1][j-1]]+a[i] dp[i][j]=max(dp[i−1][j],dp[i−1][j−1]]+a[i],我们发现, d p [ i ] [ ] dp[i][ ] dp[i][]只与 d p [ i − 1 ] [ ] dp[i-1][] dp[i−1][]有关,与前面 d p [ i − 2 ] [ ] , d p [ i − 3 ] [ ] . . . dp[i-2][],dp[i-3][]... dp[i−2][],dp[i−3][]...无关,所以滚动数组就可以将它们这些空间省下来。
那么滚动数组该如何操作呢?
可以分为两种交替滚动和自我滚动。
交替滚动
顾名思义,就是两行数组交替的进行滚动: d p [ 2 ] [ i ] , d p [ 0 ] [ i ] 和 d p [ 1 ] [ i ] 互相转移 dp[2][i],dp[0][i]和dp[1][i]互相转移 dp[2][i],dp[0][i]和dp[1][i]互相转移。这种方法的有点是简单,特别简单,只要你学过数组你就会,而且代码十分明了,不容易出错。
那么操作代码该如何写呢?给出一个伪代码:
for (日常枚举)
{交换数组 开始转移
}
如上代码是不是看起来十分简单?那么对于交换数组有两种方法,第一异或,第二直接swap。
好,现在你已经会交替滚动了。
来个例题!!!
例题:来自某某轮廓线DP的题目
题目:HDU-4064
题解:
那么好的,这是一道轮廓线DP的题目,但是我们今天的主题不是轮廓线,而是滚动数组,所以等到下次轮廓线DP的时候再重点说说吧。
先说本题主要做法吧,当然是我们的轮廓线DP,但是在做的时候如果普通的做空间直飙1e8,真的是太难受了。于是我们就要开始优化了。首先用上交 ~ 替 ~ 滚 ~ 动 ~的优化。
那么我们可以这么优化,用异或,高级点叫奇偶转变,(swap的一边去)
异或就是我们的异或符号 ^,
那么我们知道异或是不同为1,相同为0,所以拿一个数去异或1,如果是偶数,秒变奇数;如果是奇数秒变偶数。这是因为奇数末尾肯定为1,偶数末尾肯定为0,那么再异或1,就改变奇偶性了。
操作就是如下:
int cur = 0;
cur ^= 1 //变 1就是变奇数了
cur ^= 1 //变 0就是变偶数了
那么总代码就是可以写成如下样子(热心肠的我把轮廓线的部分也给加上去了)
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define m_p(i,j) make_pair(i,j)
#define pb push_back
#define pii pair<int,int>
#define mem(a,b) memset(a,b,sizeof(a))
#define fir first
#define sec second
const int eps = 1e-8;
ll POW(int a, int b)
{ll sum = 1;for (int i = 1; i <= b; ++i) sum *= a;return sum;
}
inline int read()
{int X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1);
}
inline void write(ll X)
{if(X<0) {X=~(X-1); putchar('-');}if(X>9) write(X/10);putchar(X%10+'0');
}
const int mod = 1e9 + 7;
int n, m;
string MP[15][15];
ll dp[2][(1 << 20)], P;
int cur;
int check(char a)
{if (a == 'C') return 0;if (a == 'R') return 1;return 2;
}
void dfs(int pos, int now_mask, int last_mask, ll sum, char left, int hang)
{if (pos == m + 1){sum = (sum * dp[cur ^ 1][last_mask]) % mod;dp[cur][now_mask] = (dp[cur][now_mask] + sum) % mod;return ; }int tot = 0;int num[10];char one[10], two[10], three[10];for (int i = 0; i < 4; ++i){if (pos != 1 && MP[hang][pos][i] != left) continue;char right = MP[hang][pos][(i + 2) % 4];char up = MP[hang][pos][(i + 1) % 4];char down = MP[hang][pos][(i + 3) % 4];int flag = 1;for (int j = 1; j <= tot; ++j){if(right == one[j] && up == two[j] && down == three[j]){flag = 0;++num[j];break;}}if (flag){one[++tot] = right;two[tot] = up;three[tot] = down;num[tot] = 1;}}for (int i = 1; i <= tot; ++i){int jlast_mask = (last_mask * 3 + check(two[i]));int jnow_mask = (now_mask * 3 + check(three[i]));dfs(pos + 1, jnow_mask, jlast_mask, (sum * num[i]) % mod, one[i], hang);}
}
int main(){n = read(), m = read();for (int i = 1; i <= n; ++i) for (int j = 1; j <= m; ++j) cin >> MP[i][j];P = POW(3, m);for (int i = 0; i < P; ++i) dp[0][i] = 1;cur = 0;for (int i = 1; i <= n; ++i){cur ^= 1; //开始交替mem(dp[cur], 0);dfs(1, 0, 0, 1LL, 'z', i);}ll ans = 0;for (int mask = 0; mask < P; ++mask) ans = (ans + dp[cur][mask]) % mod;write(ans); return 0;
}
自我滚动(不如交替
你已经会交替滚动了,开始上难度了----自我滚动
我们发现,其实我们把二维转换为两个一维(反正就0/1,算成俩一维吧)。
但是实际上海能进行优化。
就继续拿上面的 d p [ i ] [ j ] = m a x ( . . . ) dp[i][j] = max(...) dp[i][j]=max(...)接着举例吧。
我们是可以接着优化。
我们发现它可以优化成一维,只需要自己跟以前的自己转移就行了。
但是,注 ~ 意 ~ !!!,若上述的转移在枚举j时,一定要反过来枚举,不然可能错,因为它的结果是由同一个空间得到的,可能会影响答案正确性。
那么给出上述那个转移的代码吧(指dp[i][j] = max(…)那个)
for (int i = 1; i <= n; ++i)
{for (int j = m; j >= 1; --j){dp[j] = max(dp[j], dp[j - 1] + a[i]);}
}
完结!!!
恭喜你已经学会滚动数组了!!!
[撒花✿✿ヽ(°▽°)ノ✿]
相关文章:

滚动数组详解
滚动数组详解 何为滚动数组?滚动数组是如何优化空间的?交替滚动例题:来自某某轮廓线DP的题目 自我滚动(~~不如交替~~ 完结!!! ( 宇宙免责任书:我用的是C) 何为滚动数组? 什么是滚动…...

C 语言动态链表
线性结构->顺序存储->动态链表 一、理论部分 从起源中理解事物,就是从本质上理解事物。 -杜勒鲁奇 动态链表是通过结点(Node)的集合来非连续地存储数据,结点之间通过指针相互连接。 动态链表本身就是一种动态分配内存的…...

【Leetcode】二十、记忆化搜索:零钱兑换
文章目录 1、记忆化搜索2、leetcode509:斐波那契数列3、leetcode322:零钱兑换 1、记忆化搜索 也叫备忘录,即把已经计算过的结果存下来,下次再遇到,就直接取,不用重新计算。目的是以减少重复计算。 以前面提…...

json数据格式 继续学习
1.定义 轻量级的数据交互格式,可以按照json数据格式去组织和封装数据。 本质是一个带有特定格式的字符串。 2.功能 负责不同编程语言中的数据传递和交互。 3.json数据格式转化 """ 演示json数据和python字典之间的转换 """ impor…...

gradle 构建项目添加版本信息
gradle 构建项目添加版本信息,打包使用 spring boot 的打包插件 build.gradle 配置文件 bootJar {manifest {attributes(Project-Name: project.name,Project-Version: project.version,"project-Vendor": "XXX Corp","Built-By": &…...

vue3 学习笔记17 -- 基于el-menu封装菜单
vue3 学习笔记17 – 基于el-menu封装菜单 前提条件:组件创建完成 配置路由 // src/router/index.ts import { createRouter, createWebHashHistory } from vue-router import type { RouteRecordRaw } from vue-router export const Layout () > import(/lay…...
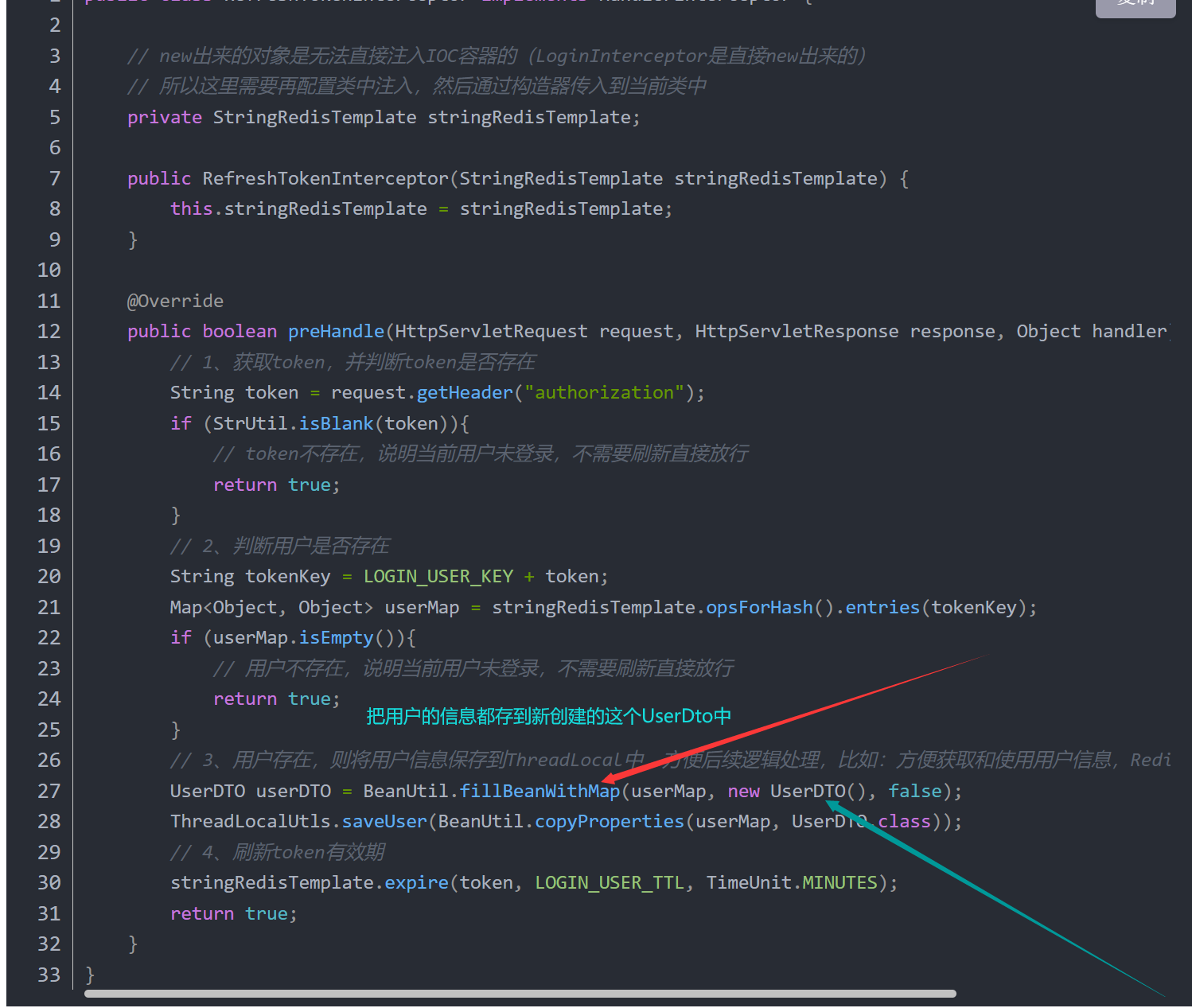
使用 Redis 实现验证码、token 的存储,用自定义拦截器完成用户认证、并使用双重拦截器解决 token 刷新的问题
可以看一下我以前做过的笔记:黑马点评 短信登录部分 基于session实现登录流程 1.发送验证码 用户在提交手机号后,会校验手机号是否合法,如果不合法,则要求用户重新输入手机号 如果手机号合法,后台此时生成对应的验…...
C语言)
反转链表 - 力扣(LeetCode)C语言
206. 反转链表 - 力扣(LeetCode)( 点击前面链接即可查看题目) /*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/ struct ListNode* reverseList(struct ListNode* head) {if(head NULL)…...

【Linux】进程间通信(1):进程通信概念与匿名管道
人与人之间是如何通信的?举个简单的例子,假如我是月老,我要为素不相识的但又渴望爱情的男女两方牵红线。我需要收集男方的信息告诉女方,收集女方的信息告诉男方,然后由男女双方来决定是否继续。对于他们而言࿰…...

Spring从入门到精通 01
文章目录 1. 依赖注入 (Dependency Injection, DI)2. 面向切面编程 (Aspect-Oriented Programming, AOP)3. 事务管理4. 简化 JDBC 开发5. 集成各种框架和技术6. 模块化和扩展性:主要的 Spring 模块:Core Container:AOP 模块:Data …...

C语言经典习题25
冒泡排序 对一维数组进行升序排序,然后在数组中输入20个数,将排序后的结果打印输出。 #include<stdio.h> #define N 20 int main() {int a[N];int i;for(i0;i<N;i) //初始化数组的数 {scanf("%d",&a);}for(i0;…...

2-47 基于matlab的时域有限差分法(FDTD法)拉夫等效原理进行时谐场外推
基于matlab的时域有限差分法(FDTD法)拉夫等效原理进行时谐场外推。外推边界距离吸收边界的距离、电磁场循环、傅立叶变换提起幅值和相位、各远区剖分点电场、方向系数计算等操作,得出可视化结果。程序已调通,可直接运行。 2-47 时域有限差分法(FDTD法) 拉…...

JupyterNotebook快捷键 自用
COMMAND MODE —————————————————————————————— Up Down cells的上下选择 A B 在上/下方插入cell C V X 复制/粘贴/剪切cell 双击D 删除所选cell Z 恢复被删除的cell 双击I Interrupt中断内核 Shift Enter 运行cell并选择下方 EDIT MODE ———…...

【我的OpenGL学习进阶之旅】讲一讲GL_TEXTURE_2D和GL_TEXTURE_EXTERNAL_OES的区别
在使用OpenGL ES进行图形图像开发时,我们常使用GL_TEXTURE_2D纹理类型,它提供了对标准2D图像的处理能力。这种纹理类型适用于大多数场景,可以用于展示静态贴图、渲染2D图形和进行图像处理等操作。 另外,有时我们需要从Camera或外部视频源读取数据帧并进行处理。这时,我们…...

Makefile 如何将生成的 .o 文件放到指定文件夹
研究了不少文章,我行通了一个,但是也不全,目前只能适用当前文件夹,如果源文件有子文件夹处理不了,还得继续研究。很多人说编译完把O文件移动走或者直接删掉。我想说的是不符合我的要求,移走或者删除O文件&a…...

聊一聊知识图谱结合RAG
因为最近在做一些关于提高公司内部使用的聊天机器人的回答准确率,并且最近微软官方也是开源了一下graphrag的源码,所以想聊一聊这个知识图谱结合rag。 rag在利用私有数据增强大模型回答的领域是一种比较典型的技术,也就是我们提出问题的时候&…...
)
Java面试锦集 之 一、Java基础(1)
一、Java基础(1) 1.final 关键字的作用? 修饰变量: 一旦被赋值,就不能再被修改,保证了变量值的稳定性。 例: final int NUMBER 10; //之后就不能再改变 NUMBER 的值了。修饰方法:…...

【leetcode】排列序列
给出集合 [1,2,3,...,n],其所有元素共有 n! 种排列。 按大小顺序列出所有排列情况,并一一标记,当 n 3 时, 所有排列如下: "123""132""213""231""312""321" 给定…...

【Cesium开发实战】视频融合功能的实现,可自定义位置和视频路径
Cesium有很多很强大的功能,可以在地球上实现很多炫酷的3D效果。今天给大家分享一个视频融合功能。 1.话不多说,先展示 视频融合 2.设计思路 点击绘制开始在地图上绘制视频融合的点位,形成视频播放的区域,双击弹框输入名称和要播放视频的路径,即可对应区域播放对应视频,…...

【秋招笔试题】小明的美食
解析:思维题。由于需要互不相同,每次操作取重复的值与最大值相加即可,这样即可保证相加后不会新增重复的值。因此统计重复值即可。 #include <iostream> #include <algorithm>using namespace std; const int maxn 1e5 5; int…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...
