LeetCode分类刷题----动态规划
动态规划
- 509.斐波那契数列
- 70.爬楼梯
- 746.使用最小花费怕楼梯
- 62.不同路径
- 63.不同路径||
- 343.整数拆分
- 96.不同的二叉搜索树
- 01背包问题
- 416.分割等和子集
- 1049.最后一块石头的重量||
- 494.目标和
- 474.一和零
- 完全背包问题
- 518.零钱兑换||
- 377.组合总和IV
- 322.零钱兑换
- 279.完全平方数
- 139.单词拆分
- 打家劫舍
- 198.打家劫舍
- 213.打家劫舍||
- 买卖股票
- 121.买卖股票的最佳时机
- 300.最长递增子序列
- 674.最长连续递增序列
- 718.最长重复子数组
- 1143.最长公共子序列
- 1035.不相交的线
- 53.最大子数组和
- 392.判断子序列
- 115.不同的子序列
- 583.两个字符串的删除操作
- 72.编辑距离
- 647.回文子串
- 516.最长回文子序列
509.斐波那契数列

思路:
用一个数组把每个数字都存起来即可。
public int fib(int n) {if(n==0) {return 0;}if(n==1) {return 1;}int []dp=new int[n];dp[0]=1;dp[1]=1;for(int i=2;i<n;i++) {dp[i]=dp[i-1]+dp[i-2];}return dp[n-1];}
70.爬楼梯

思路:
也是用递推的方法斐波那契数列。
public int climbStairs(int n) {int []dp=new int[n+1];if(n==1) {return 1;}if(n==2) {return 2;}dp[1]=1;dp[2]=2;for(int i=3;i<n+1;i++) {dp[i]=dp[i-1]+dp[i-2];}return dp[n];}
746.使用最小花费怕楼梯

思路:
当前台阶 的最小花费体力是上一层的最小体力,加上跳出上一层需要花费的体力。或者上两层的最小体力加上跳出上两层需要花费的最小体力。这两个取一个最小值。因为题目要求可以从第0阶开始跳,也可以从第1阶开始跳,所以第0阶和第1阶的初始值为0.
public int minCostClimbingStairs(int[] cost) {int dp[]=new int[cost.length+1];dp[0]=0;dp[1]=0;for(int i=2;i<=cost.length;i++) {dp[i]=Math.min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2]);}return dp[cost.length];}
62.不同路径
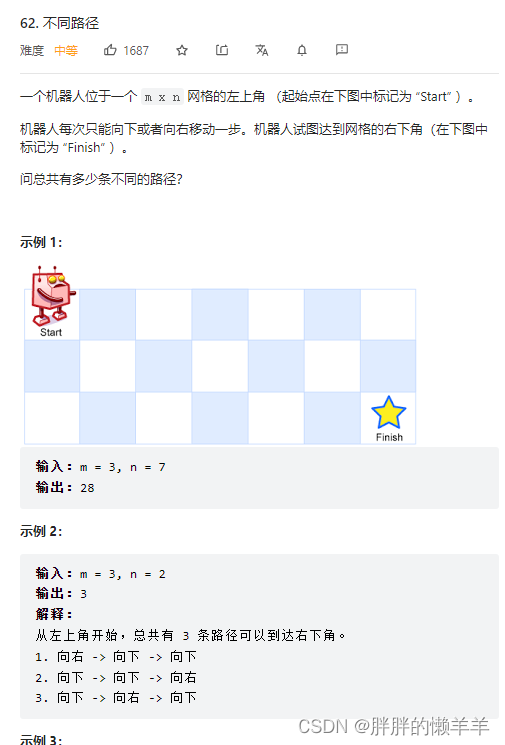
思路:
首先确定dp[i][j]的含义。
代表从头到达这个点有多少条路径。
然后递推公式dp[i][j]=dp[i-1][j]+dp[i][j-1]。
初始化首先初始化第一行和第一列,方法都是1。
然后调用递推公式即可。
public int uniquePaths(int m, int n) {int dp[][]=new int[m][n];//代表要达到这个位置需要多少路径//初始化for(int i=0;i<m;i++) {dp[i][0]=1;}for(int i=0;i<n;i++) {dp[0][i]=1;}for(int i=1;i<m;i++) {for(int j=1;j<n;j++) {dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[m-1][n-1];63.不同路径||

思路:
当遇到没有障碍的时候再初始化,如果遇到障碍,后边的就不用初始化了。
然后递推公式中如果不遇到障碍再递推,如果遇到障碍直接初始化为0即可。
public int uniquePathsWithObstacles(int[][] obstacleGrid) {//初始化。如果遇到有障碍直接停下int m=obstacleGrid.length;int n=obstacleGrid[0].length;int dp[][]=new int[m][n];//如果遇到初始位置和终止位置有障碍,直接返回0,因为此路就不通了。if(obstacleGrid[0][0]==1||obstacleGrid[m-1][n-1]==1) {return 0;}//进行初始化,当没障碍的时候才进行初始化for(int i=0;i<m&&obstacleGrid[i][0]==0;i++) {dp[i][0]=1;}for(int i=0;i<n&&obstacleGrid[0][i]==0;i++) {dp[0][i]=1;}for(int i=1;i<m;i++) {for(int j=1;j<n;j++) {dp[i][j]=(obstacleGrid[i][j]==0)?dp[i-1][j]+dp[i][j-1]:0;}}return dp[m-1][n-1];}
343.整数拆分
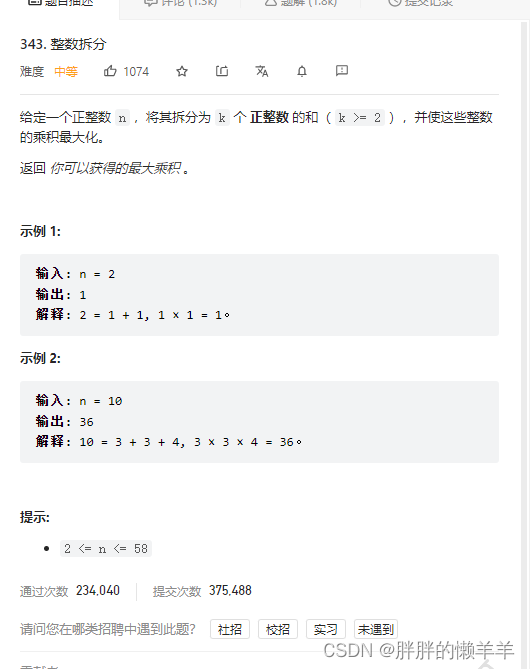
思路:
dp[i]数组的含义就是i能拆分到的数值的最大值。
所以从3开始迭代。每个数字再进行拆分。
从1开始。看j*(i-j)。j*(dp[i-j]),dp[i]哪个大。dp[i-j]后边就相当于很多数字相乘。
public int integerBreak(int n) {if(n==1) {return 0;}if(n==2) {return 1;}int dp[]=new int[n+1];//代表数字i拆分的最大值.//初始化dp[0]=0;dp[1]=0;dp[2]=1;for(int i=3;i<=n;i++) {for(int j=1;j<i;j++) {dp[i]=Math.max(dp[i], Math.max(j*(i-j),j* dp[i-j]));}}return dp[n];}
96.不同的二叉搜索树
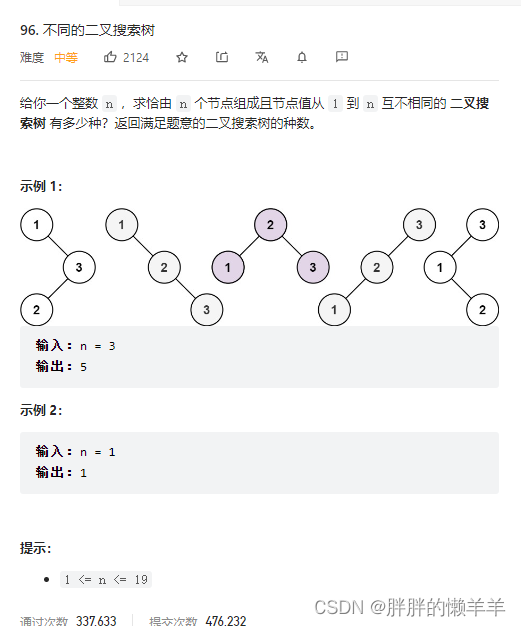
思路:
大的节点都是由小的节点推出来的。让1到i分别做根节点,然后生成树的种类是左子树的种类乘以右子树的种类。
public int numTrees(int n) {int dp[]=new int[n+1];//代表n个节点组成的有多少个情况//初始化dp[0]=1;dp[1]=1;for(int i=2;i<=n;i++) {for(int j=1;j<=i;j++) {//j代表j作为根节点的情况,那么左子树有j-1个节点,右子树有i-j个节点dp[i]+=dp[j-1]*dp[i-j];}}return dp[n];}
01背包问题
416.分割等和子集

思路:
转换成背包问题,就是当这个背包装的容量最大时能不能满足target的目标值。
先遍历物品再遍历背包。遍历背包的时候要从后往前遍历,因为下一层的时候可能要用到左上角的值。注意dp数组的含义
public boolean canPartition(int[] nums) {//判断有没有满足平分的数组if(nums==null||nums.length==0) {return false;}int sum=0;for(int num:nums) {sum+=num;}if(sum%2==1) {return false;//如果是奇数的话,肯定是不能平分的}int target=sum/2;int []dp=new int[target+1];//dp数组代表当前容量所能装的最大值for(int i=0;i<nums.length;i++) {//先遍历物品,再遍历背包for(int j=target;j>=nums[i];j--) {dp[j]=Math.max(dp[j], dp[j-nums[i]]+nums[i]);}}return dp[target]==target;}
1049.最后一块石头的重量||

思路:
将石头尽量分成大小相等的两堆,然后分配一个sum/2的容量的背包去装石头这样遍历完整个数组后,背包里装的是尽可能多的石头。装完了之后让剩下的一堆石头减去这堆石头就是剩余的最小的石头了。
public int lastStoneWeightII(int[] stones) {if(stones==null||stones.length==0) {return 0;}int sum=0;for(int stone:stones) {sum+=stone;}int target=sum/2;int []dp=new int [target+1];//dp数组代表当前容量所能装的最大值for(int i=0;i<stones.length;i++) {for(int j=target;j>=stones[i];j--) {dp[j]=Math.max(dp[j],dp[j-stones[i]]+stones[i]);}}return sum-dp[target]-dp[target];//将石头分成两堆,用大的一堆减去小的一堆}
494.目标和
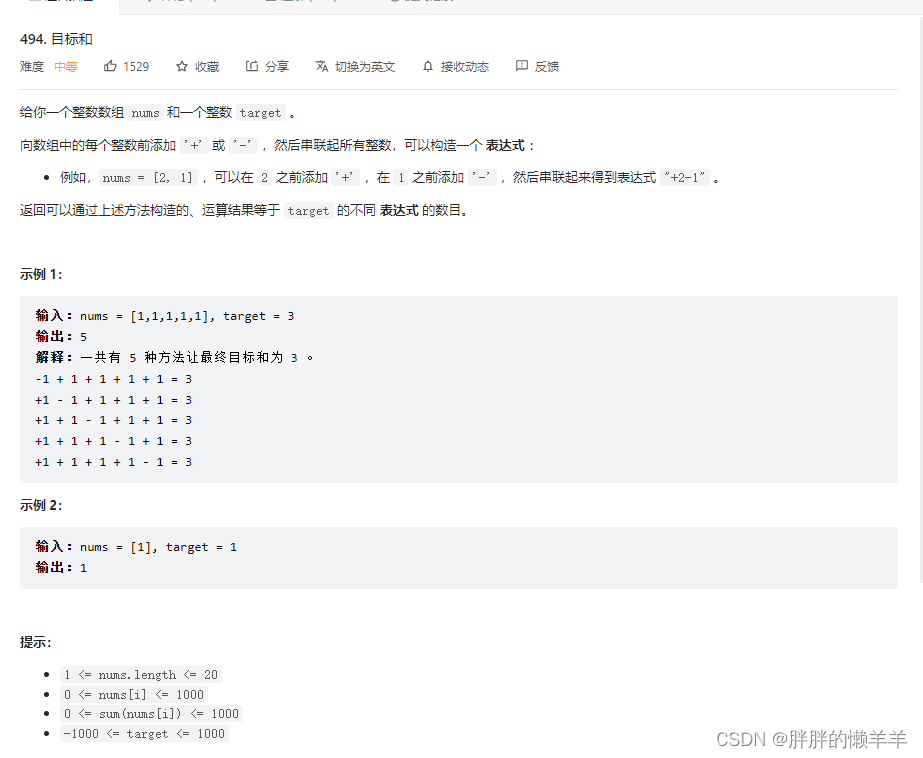
思路:
将整个数组分成正数和负数两部分。
public int findTargetSumWays(int[] nums, int target) {//将数组分成两堆,左边是正数,右边是负数,则有左+右=sum,左-右=target 然后我们就可以求出左边的数 左=(sum+target)/2//左边的数是正数,给一个这样大小的背包,我们去求有多少种这样的方法可以装满这个背包,就是有多少种这样组合的正数可以放在左边//dp[j]的含义。装满j容量大小的背包有dp[j]种方法int sum=0;for(int num:nums) {sum+=num;}//如果target过大 sum将无法满足if ( target < 0 && sum < -target) return 0;if ((target + sum) % 2 != 0) return 0;int temp=(sum+target)/2;int[] dp=new int[temp+1];//递推公式,dp[5]=dp[4]+dp[3]+dp[2]+dp[1]+dp[0] 因为有1的话,还有dp[4]种方法,以此类推就可以了dp[0]=1;for(int i=0;i<nums.length;i++) {//先遍历物品for(int j=temp;j>=nums[i];j--) {dp[j]+=dp[j-nums[i]];}}return dp[temp];}
474.一和零

思路:
这道题的背包变成二维的了。
背包容量有m个0和n个1.
需要统计出每个字符串包含的0和1的个数。然后再去迭代。
public int findMaxForm(String[] strs, int m, int n) {int dp[][]=new int[m+1][n+1];//dp代表当前背包的容量能最多能放多少个含x个0,y个1的元素。m+1,n+1代表二维数组的容量int zeronum;int onenum;for(String str:strs) {zeronum=0;onenum=0;for(char c:str.toCharArray()) {if(c=='0') {zeronum++;}else if(c=='1') {onenum++;}}for(int i=m;i>=zeronum;i--) {for(int j=n;j>=onenum;j--) {dp[i][j]=Math.max(dp[i-zeronum][j-onenum]+1,dp[i][j] );}}}return dp[m][n];}
完全背包问题
518.零钱兑换||

思路:
已经给了你背包容量的大小,这里只不过是一个物品可以被装很多次,背包从小到大遍历就行了。前提是容量得等于当前硬币的大小。
public int change(int amount, int[] coins) {//递推表达式int[] dp = new int[amount + 1];//初始化dp数组,表示金额为0时只有一种情况,也就是什么都不装dp[0] = 1;for (int i = 0; i < coins.length; i++) {for (int j = coins[i]; j <= amount; j++) {//从小到大去遍历时完全背包的问题dp[j] += dp[j - coins[i]];}}return dp[amount];}
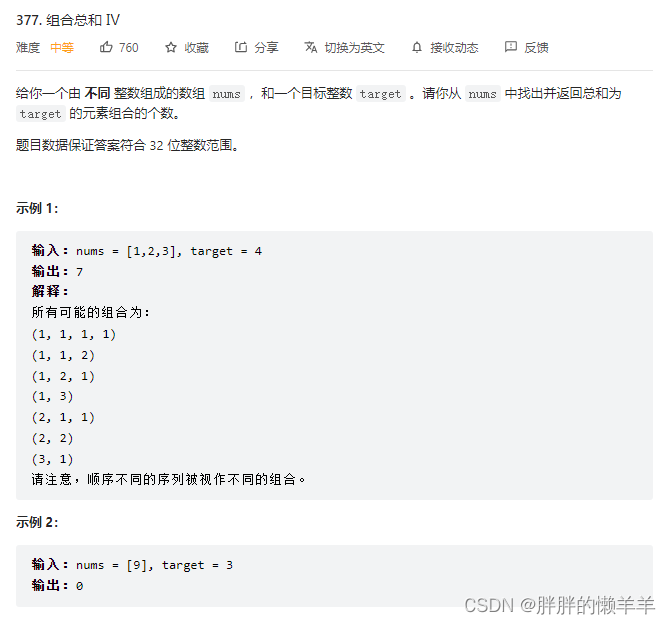
377.组合总和IV
思路:
这道题要强调元素的顺序。所以先遍历背包,再遍历物品。然后如果背包容量大于等于物品的话,就把它加进去。
public int combinationSum4(int[] nums, int target) {//因为这个组合强调遍历顺序了,所以不同顺序的物品也要算作不同的结果int dp[]=new int[target+1];//初始化dp[0]=1dp[0]=1;for(int i=0;i<=target;i++) {//先遍历背包for(int j=0;j<nums.length;j++) {if(i>=nums[j]) {//如果dp[i]+=dp[i-nums[j]];}}}return dp[target];}
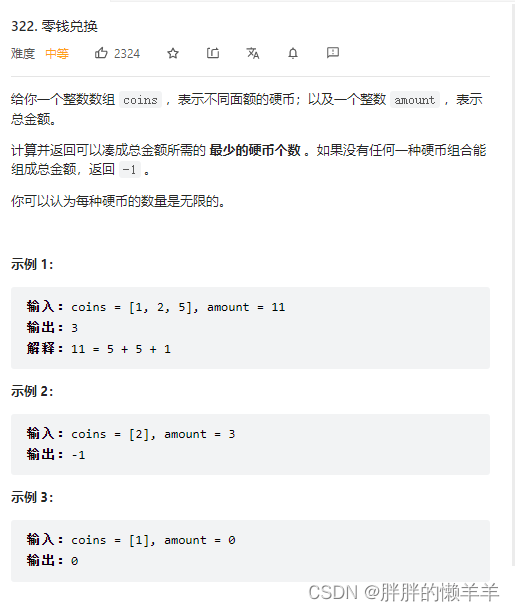
322.零钱兑换
思路:
要保证最小的数组,把数组初始化成最大值,然后每次去迭代dp[j]都去选取最小的值。
dp[j]的含义。装满容量为j的背包最小的元素要多少。
public int coinChange(int[] coins, int amount) {int dp[]=new int[amount+1];//初始化dp数组为最大的值for(int i=0;i<amount+1;i++) {dp[i]=Integer.MAX_VALUE;}//初始化dp[0]=0;for(int i=0;i<coins.length;i++) {//先遍历物品,再遍历背包for(int j=coins[i];j<=amount;j++) {//只有dp[j-coins[i]]不是初始最大值时,该位才有选择的必要if(dp[j-coins[i]]!=Integer.MAX_VALUE) {dp[j]=Math.min(dp[j], dp[j-coins[i]]+1);}}}return dp[amount]==Integer.MAX_VALUE?-1:dp[amount];}
279.完全平方数

思路:
用完全平方数做物品,然后背包容量是目标数大小,然后每次更新最小的数就可以了。
public int numSquares(int n) {//生成完全平方数做物品int[] dp=new int[n+1];//初始化for(int i=0;i<=n;i++) {dp[i]=Integer.MAX_VALUE;}dp[0]=0;for(int i=1;i*i<=n;i++) {//先遍历物品for(int j=i*i;j<=n;j++) {//再遍历背包if(dp[j-(i*i)]!=Integer.MAX_VALUE) {dp[j]=Math.min(dp[j], dp[j-i*i]+1);}}}return dp[n];}
139.单词拆分

思路:
完全背包问题。将字符串想象成一个背包,每个单词是物品。判断物品能不能装满这个背包即可。因为字符串有顺序问题。所以是排列问题,先遍历背包。再遍历物品。判断j,i之间的字符串在不在物品里边即可。
dp[0]初始化为true,其他初始化为false。
public boolean wordBreak(String s, List<String> wordDict) {HashSet<String> set=new HashSet<>(wordDict);boolean[] valid = new boolean[s.length() + 1];valid[0] = true;for (int i = 1; i <= s.length(); i++) {for (int j = 0; j < i && !valid[i]; j++) {if (set.contains(s.substring(j, i)) && valid[j]) {valid[i] = true;}}}return valid[s.length()];}
打家劫舍
198.打家劫舍

思路:
确定dp数组含义,dp[i]表示从下标i以前所能偷得的最大金币数。
初始化dp[0]和dp[1]。
然后i需要从前两个位置来确定偷还是不偷,这两个状态中去取一个最大值。
public int rob(int[] nums) {if(nums.length==1) {return nums[0];}int []dp=new int[nums.length];//dp[]数组含义,偷到dp[i]的时候所能偷的最大数量//初始化dp[0]=nums[0];//只能偷一个的话肯定是当前的最大值dp[1]=Math.max(nums[0], nums[1]);//偷两个元素的话是偷前两个元素的最大值for(int i=2;i<nums.length;i++) {dp[i]=Math.max(dp[i-2]+nums[i], dp[i-1]);//当前的结果是偷i的结果还是不偷i的结果}return dp[nums.length-1];}
213.打家劫舍||

思路:
这道题就是在打家劫舍的基础上判断有没有环,可以分两种情况来考虑,第一种情况就是考虑第一个元素,第二种情况就是考虑最后一个元素。然后这两种情况取一个最大值。
public int rob(int[] nums) {if (nums == null || nums.length == 0)return 0;int len = nums.length;if (len == 1)return nums[0];return Math.max(robAction(nums, 0, len - 1), robAction(nums, 1, len));}int robAction(int[] nums, int start, int end) {int x = 0, y = 0, z = 0;for (int i = start; i < end; i++) {y = z;z = Math.max(y, x + nums[i]);x = y;}return z;}
买卖股票
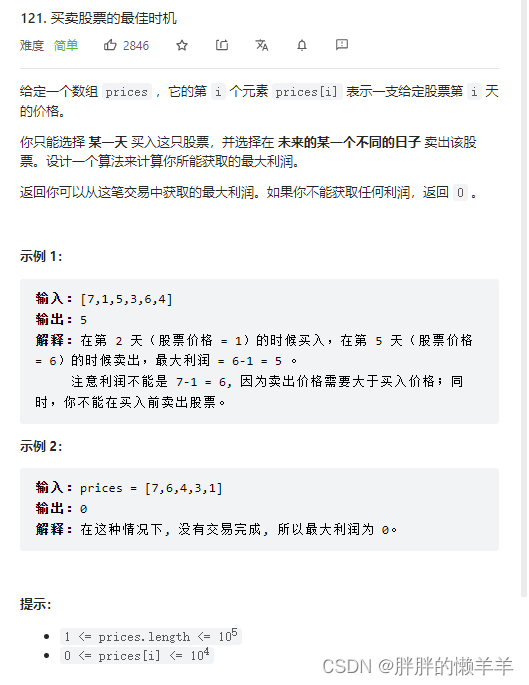
121.买卖股票的最佳时机
思路:
定义两个状态,一个是持有股票的状态,一个是不持有股票的状态,这两个状态都可以通过前一天推出来。
然后找到不持有股票状态的最大值即可,
public int maxProfit(int[] prices) {//dp数组含义dp[i][0]表示持有股票的最大金钱,持有股票不代表就是这天买的,也可能是前几天买的//dp[i][1]表示不持有股票的最大金钱,卖出股票不代表就是这天卖的,也可能是前几天卖的int [][]dp=new int[prices.length][2];//dp数组初始化dp[0][0]=-prices[0];//持有股票的最大金钱就是这天卖的dp[0][1]=0;//表示不持有股票的最大金钱for(int i=1;i<prices.length;i++) {dp[i][0]=Math.max(dp[i-1][0], -prices[i]);//可能是前几天就买了,也可能是当天买的dp[i][1]=Math.max(dp[i-1][1], dp[i][0]+prices[i]);//可能是当天卖的}return dp[prices.length-1][1];}
300.最长递增子序列

思路:
从第二个数字开始遍历,然后里边再套一层循环,从i之前的元素开始。如果当前的字母比前边的数字大。那么就取一个最大值。最后输出数组里边的最大值即可。
public static int lengthOfLIS(int[] nums) {//dp数组定义dp[i]以i为结尾的最长递增子序列的最大值int []dp=new int[nums.length];//初始化Arrays.fill(dp,1);dp[0]=1;for(int i=1;i<nums.length;i++) {for(int j=0;j<i;j++) {if(nums[i]>nums[j]) {dp[i]=Math.max(dp[i], dp[j]+1);}}}//从dp数组中再找到一个最大值int result = 0;for(int i=0;i<nums.length;i++) {result=Math.max(result,dp[i] );}return result;}
674.最长连续递增序列

思路:
每一个元素和上一个元素比较,如果满足条件就+1.如果不满足,就初始化为1.
public int findLengthOfLCIS(int[] nums) {//定义dp数组,dp[i]代表以i为结尾的最长连续递增子序列int dp[]=new int[nums.length];//初始化dp[0]=1;//遍历顺序:从左到右for(int i=1;i<nums.length;i++) {if(nums[i]>nums[i-1]) {dp[i]=dp[i-1]+1;}else {dp[i]=1;}}int result = 0;for(int i=0;i<dp.length;i++) {result=Math.max(result, dp[i]);}return result;}
718.最长重复子数组

思路:
定义dp数组含义
dp[i][j]代表数组1到i-1,数组2到j-1的最长重复子数组。
遍历顺序,先遍历数组1,然后遍历数组2如果nums1[i-1]==nums[j-1]。更新dp数组。
结果返回dp数组的最大值即可。
public int findLength(int[] nums1, int[] nums2) {//dp数组定义代表dp[i][j]代表数组1到i-1,数组2到i-2的最长重复子数组int dp[][]=new int[nums1.length+1][nums2.length+1];//初始化int result=0;//记录最大的结果for(int i=1;i<nums1.length+1;i++) {for(int j=1;j<nums2.length+1;j++) {if(nums1[i-1]==nums2[j-1]) {dp[i][j]=dp[i-1][j-1]+1;}result=Math.max(result, dp[i][j]);}}return result;}
1143.最长公共子序列

思路:
这道题和前一道的区别是这道题不要求连续了。所以要考虑字符串不相等的情况,不相等的时候可以从上边或者左边推出来。
public int longestCommonSubsequence(String text1, String text2) {int dp[][]=new int[text1.length()+1][text2.length()+1];//确定dp数组含义//dp[i][j]表示字符串1[0,i-1]字符串2[0,j-1]的最长重复子数组,因为这里不考虑需要字符连续的情况。所以需要考虑不相同的qingk for(int i=1;i<=text1.length();i++) {for(int j=1;j<=text2.length();j++ ) {if(text1.charAt(i-1)==text2.charAt(j-1)) {dp[i][j]=dp[i-1][j-1]+1;}else {dp[i][j]=Math.max(dp[i-1][j], dp[i][j-1]);}}}return dp[text1.length()][text2.length()];}
1035.不相交的线

思路:
其实就是在求两个数字数组的最长公共子序列。
public int maxUncrossedLines(int[] nums1, int[] nums2) {int dp[][]=new int[nums1.length+1][nums2.length+1];for(int i=1;i<=nums1.length;i++) {for(int j=1;j<=nums2.length;j++) {if(nums1[i-1]==nums2[j-1]) {dp[i][j]=dp[i-1][j-1]+1;}else {dp[i][j]=Math.max(dp[i-1][j], dp[i][j-1]);}}}return dp[nums1.length][nums2.length];}
53.最大子数组和

思路:
dp[i]是以i结尾的最大数组和。当前这个值由dp[i-1]+nums[i],nums[i]中两个数之间选一个最大的。
public int maxSubArray(int[] nums) {int dp[]=new int[nums.length];//dp数组含义,以i为结尾的最大子数组和if(nums.length==1) {return nums[0];}int result=Integer.MIN_VALUE;//初始化dp[0]=nums[0];for(int i=1;i<nums.length;i++) {dp[i]=Math.max(nums[i], dp[i-1]+nums[i]);result=Math.max(result, dp[i]);}return result;}
392.判断子序列

思路:
这道题就是求最长公共子序列,求出最长公共子序列的长度,然后再和最短的子串长度进行笔记,然后判断这两个是不是相等即可。
public boolean isSubsequence(String s, String t) {int dp[][]=new int[s.length()+1][t.length()+1];//确定dp数组的含义,dp[i][j]表示字符串1以i-1为结尾,字符串2以j-1为结尾的最长子序列长度for(int i=1;i<=s.length();i++) {for(int j=1;j<=t.length();j++) {if(s.charAt(i-1)==t.charAt(j-1)) {dp[i][j]=dp[i-1][j-1]+1;}else {dp[i][j]=Math.max(dp[i-1][j], dp[i][j-1]);}}}return dp[s.length()][t.length()]==s.length();}
115.不同的子序列

思路:
记住dp定义。
然后dp可以有两个状态推过来,然后记住下一次操作。当s[i-1]和t[j-1]相等时,可以选择用它还可以选择不用它。
public int numDistinct(String s, String t) {int dp[][]=new int[s.length()+1][t.length()+1];//确定dp数组的含义,dp[i][j]表示以i-1结尾的字符串中有多少个以j-1结尾的子串//初始化dp[0][0]=1;dp[0][1]=0;dp[1][0]=1;for (int i = 0; i < s.length() + 1; i++) {dp[i][0] = 1;}for(int i=1;i<=s.length();i++) {for(int j=1;j<=t.length();j++) {if(s.charAt(i-1)==t.charAt(j-1)) {//这里分为用i-1的情况和不用i-1的情况,例如bagg,bag.dp[i][j]=dp[i-1][j-1]+dp[i-1][j];}else {dp[i][j]=dp[i-1][j];//不相等的话就往前推一位}}}return dp[s.length()][t.length()];}
583.两个字符串的删除操作

思路:
如果相同,dp数组就按照dp[i-1][j-1]
如果比较的字符串不同,那么dp数组就在删上一个、删下一个、两个都删里边选一个比较小的。
public int minDistance(String word1, String word2) {int dp[][]=new int[word1.length()+1][word2.length()+1];//dp数组含义,dp[i][j]以i-1结尾的word1和j-1结尾的word2要达到相同的长度需要删除几个元素//初始化for(int i=0;i<=word1.length();i++) {dp[i][0]=i;}for(int j=0;j<=word2.length();j++) {dp[0][j]=j;}for(int i=1;i<=word1.length();i++) {for(int j=1;j<=word2.length();j++) {if(word1.charAt(i-1)==word2.charAt(j-1)) {//如果当前两个字母相等的话,删不删都无所谓了dp[i][j]=dp[i-1][j-1];}else {//否则,就要取删i-1,删j-1,还是都删中最小的一个dp[i][j]=Math.min(dp[i-1][j]+1, Math.min(dp[i][j-1]+1, dp[i-1][j-1]+2));}}}return dp[word1.length()][word2.length()];}
72.编辑距离

思路:
dp[][]数组定义
dp数组初始化
根据上一个的状态推出dp[i][j]。要不就删一个,要不就更改一个。
public int minDistance(String word1, String word2) {int dp[][]=new int[word1.length()+1][word2.length()+1];//dp数组含义,dp[i][j]表示以i-1结尾的word1要变成j-1为结尾的word2最少操作的次数//初始化for(int i=0;i<=word1.length();i++) {dp[i][0]=i;}for(int j=0;j<=word2.length();j++) {dp[0][j]=j;}for(int i=1;i<=word1.length();i++) {for(int j=1;j<=word2.length();j++) {if(word1.charAt(i-1)==word2.charAt(j-1)) {//如果当前两个字母相等的话,最小移动次数就是去掉这两个字母的移动次数dp[i][j]=dp[i-1][j-1];}else {//否则,就要取删i-1,删j-1,还是更改一个的最小次数dp[i][j]=Math.min(dp[i-1][j]+1, Math.min(dp[i][j-1]+1, dp[i-1][j-1]+1));}}}return dp[word1.length()][word2.length()];}
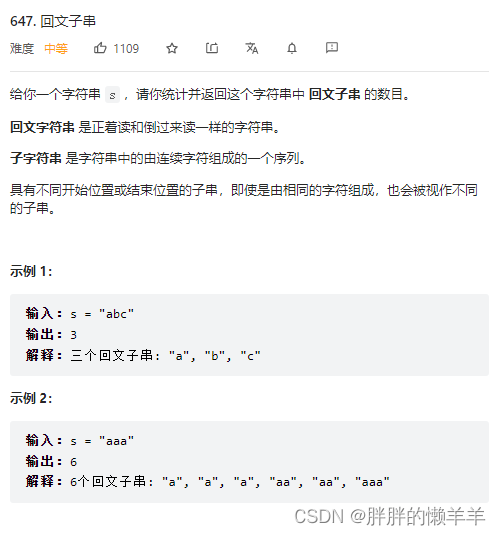
647.回文子串
思路:
定义dp数组的含义。
然后当s[i]=s[j]时,分析三种情况。
如果满足回文串的时候,返回三种数量即可。
public int countSubstrings(String s) {boolean dp[][]=new boolean[s.length()][s.length()];//dp[i][j]含义,表示以i为开头,以j为结尾的子串是不是回文串int result=0;//初始化都初始为false‘//遍历顺序,从左下角到右上角开始遍历for(int i=s.length()-1;i>=0;i--) {for(int j=i;j<s.length();j++) {if(s.charAt(i)==s.charAt(j)) {//如果两个字母相等if(j-i<=1) {//一定是回文串,可能是一个字符串,也可能是两个相同的字符串result++;dp[i][j]=true;}else if(dp[i+1][j-1]) {//如果相差距离大于1,里面的子串是回文串,那么这个也就是回文串了result++;dp[i][j]=true;}}}}return result;}
516.最长回文子序列
思路:
定义dp数组含义,然后dp数组可以从i+1,和j-1推出。
或者只考虑一端的数子,然后取这两个较大的值。
最后取一个较大的结果即可。
public int longestPalindromeSubseq(String s) {int dp[][]=new int[s.length()+1][s.length()+1];//dp数组含义表示dp[i][j]从i开始到j结束的最长的回文子序列//初始化for(int i=0;i<s.length();i++) {dp[i][i]=1;}//遍历顺序从左下角到右上角遍历for(int i=s.length()-1;i>=0;i--) {for(int j=i+1;j<s.length();j++) {if(s.charAt(i)==s.charAt(j)) {//如果两个字母相等的话,那么这个字符串也是一个回文字符串dp[i][j]=dp[i+1][j-1]+2;}else {//如果不是,取两个之间较大的一个dp[i][j]=Math.max(dp[i+1][j], dp[i][j-1]);}}}return dp[0][s.length()-1];}
相关文章:

LeetCode分类刷题----动态规划
动态规划509.斐波那契数列70.爬楼梯746.使用最小花费怕楼梯62.不同路径63.不同路径||343.整数拆分96.不同的二叉搜索树01背包问题416.分割等和子集1049.最后一块石头的重量||494.目标和474.一和零完全背包问题518.零钱兑换||377.组合总和IV322.零钱兑换279.完全平方数139.单词拆…...

今年好像没有金三银四了?
大家好,我是记得诚。 金三银四,是换工作的高峰期,新的一年结束了,在年前拿完年终奖,在年后3月和4月换个满意的工作。 单从我公司来看,目前还没有一个人离职,往年离职率是要高一些的。 还有我…...
【C++】入门知识之 函数重载
前言提到重载这个词,我们会想到什么呢?重载有一种一词多义的意思,中华文化博大精深,之前有一个笑话,中国的乒乓球谁都打不过,男足谁都打不过,哈哈哈这也是非常有意思的,但是今天我们…...
文心一言发布,你怎么看?chatGPT
百度全新一代知识增强大语言模型“文心一言”于2021年3月16日正式发布,作为一款自然语言处理技术,它引起了广泛的关注和讨论。 首先,文心一言是一款具有重大意义的自然语言处理技术。在人工智能领域,自然语言处理技术一直是一个难…...

字符函数和字符串函数【上篇】
文章目录🎖️1.函数介绍📬1.1. strlen📬1.2. strcpy📬1.3. strcat📬1.4. strcmp📬1.5. strncpy📬1.6. strncat📬1.7. strncmp🎖️1.函数介绍 📬1.1. strlen …...

list的模拟实现(模仿STL)
目录 一、模拟实现前的准备 1.list结构认识 2.迭代器的实现不同 3.如何实现需要的功能 二.结点类实现 三.迭代器实现 1.实现前的问题 2._list_iterator类的成员变量和构造函数 3.*和->运算符重载 4.前置和后置的实现 5.前置--和后置-- 6.和!运算符重载 四.list类的实现 1.li…...

05-STM32F1 - 串行通信SPI
SPI STM-SPI作为主机,从机 SPI的时钟,最高为Pclk/2,SPI1最高为36Mhz,SPI2最高为18Mhz。 SPI的四种模式 CPOL CPHA,数据帧8~16位,LSB,MSB 全双工,双向单线,单线 物理层 接口标准…...

【Pytorch】Tensor的分块、变形、排序、极值与in-place操作
本文参加新星计划人工智能(Pytorch)赛道:https://bbs.csdn.net/topics/613989052 这是目录Tensor的分块Tensor的变形Tensor的排序Tensor的极值Tensor的in-place操作Tensor是PyTorch中用于存储和处理多维数据的基本数据结构,它类似于NumPy中的ndarray&…...

数组栈的实现
个人主页:平行线也会相交 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创 收录于专栏【数据结构初阶(C实现)】 目录所有接口函数栈的初始化在栈顶放数据释放数据删除数据取栈顶的数据判断栈取区是否为…...
*p++,*(p++),*++p,(*p)++区别?
*p++:等同于:*p; p += 1; 解析:由于和++的运算优先级一样,且是右>结合。故p++相当于*(p++),p先与++结合,>然后p++整体再与结合。前面陈述是一种最 常见的错误,很多初学者也是这么理解的。 但是,因为++后置的时候,本身含义就是先 运算后增加1(运算指的是p++作为…...
又一个线上偶发问题-系统短暂无法获取到Redis连接
概述 最近不知道咋回事,老是在线上遇到偶发的故障,它突然出现,又很快消失了。 在2023年3月11下午差不多六点左右,我正在工位上喝着香味扑鼻的金骏眉红茶,突然接到了一个电话,拿起手机一看,是阿里…...
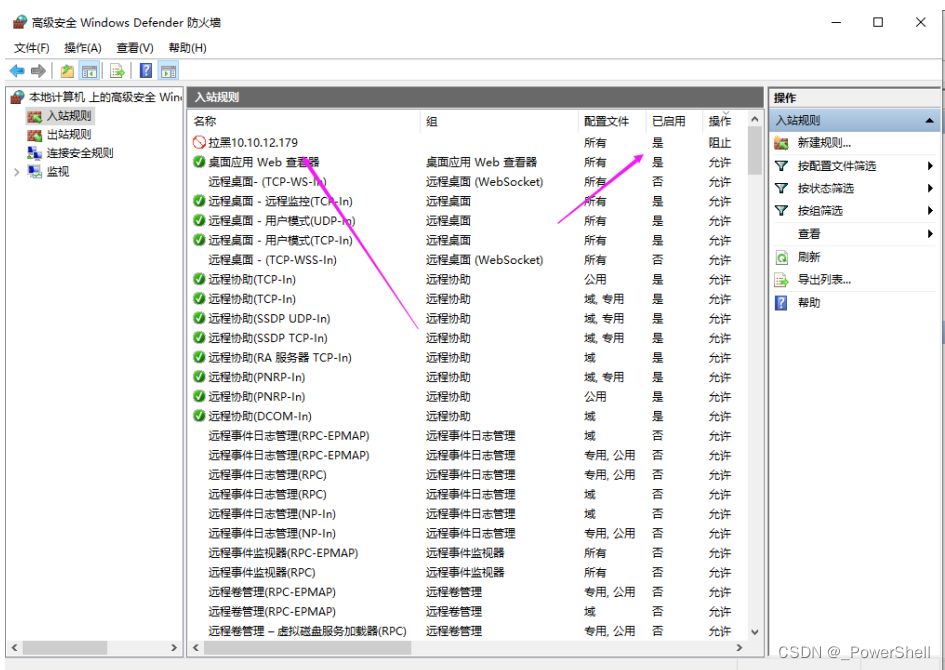
[ 系统安全篇 ] 拉黑IP - 火绒安全软件设置IP黑名单 windows使用系统防火墙功能设置IP黑名单
🍬 博主介绍 👨🎓 博主介绍:大家好,我是 _PowerShell ,很高兴认识大家~ ✨主攻领域:【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 养成习…...
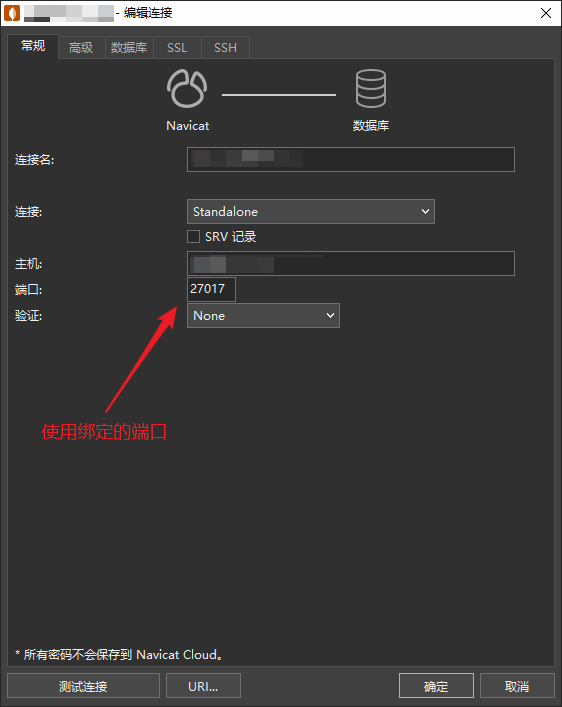
MongoDB【部署 01】mongodb最新版本6.0.5安装部署配置使用及mongodb-shell1.8.0安装使用(云盘分享安装文件)
云盘分享文件: 链接:https://pan.baidu.com/s/11sbj1QgogYHPM4udwoB1rA 提取码:l2wz 1.mongodb简单介绍 MongoDB的 官网 内容还是挺丰富的。 是由 C语言编写的,是一个基于分布式文件存储的开源数据库系统。在高负载的情况下&…...

算法竞赛必考算法——动态规划(01背包和完全背包)
动态规划(一) 目录动态规划(一)1.01背包问题1.1题目介绍1.2思路一介绍(二维数组)1.3思路二介绍(一维数组) 空间优化1.4思路三介绍(输入数据优化)2.完全背包问题2.1题目描述:2.2思路一(朴素算法)2.3思路二(将k优化处理掉)2.4思路三(优化j的初始条件)总结1.01背包问题…...
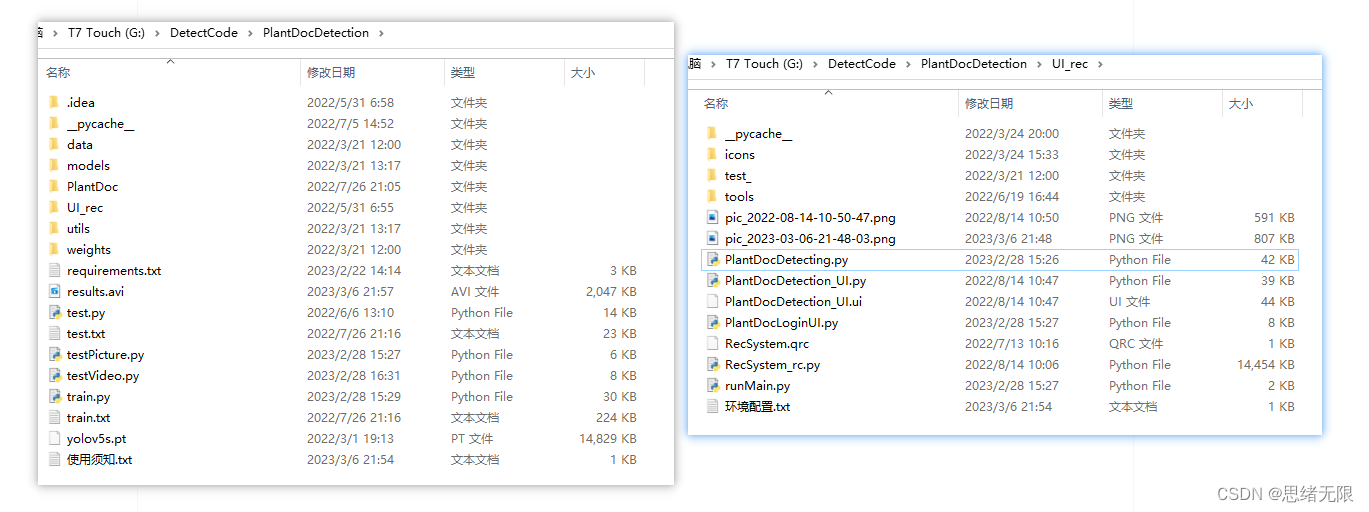
基于深度学习的农作物叶片病害检测系统(UI界面+YOLOv5+训练数据集)
摘要:农作物叶片病害检测系统用于智能检测常见农作物叶片病害情况,自动化标注、记录和保存病害位置和类型,辅助作物病害防治以增加产值。本文详细介绍基于YOLOv5深度学习模型的农作物叶片病害检测系统,在介绍算法原理的同时&#…...
QT入门Item Views之QListView
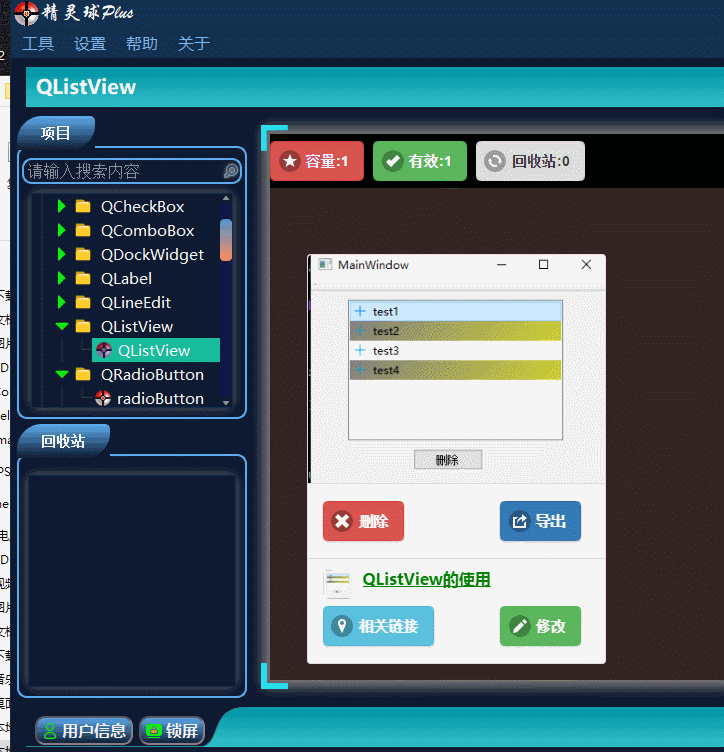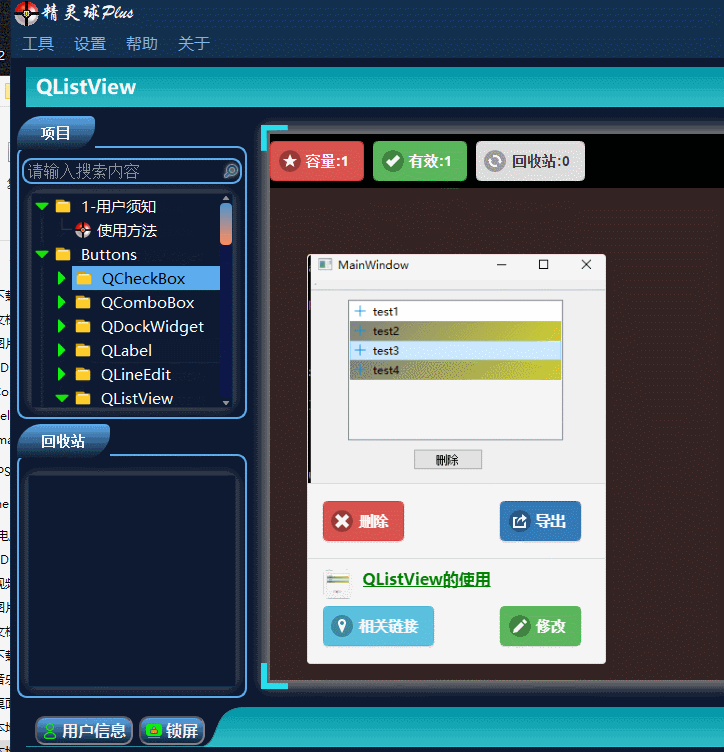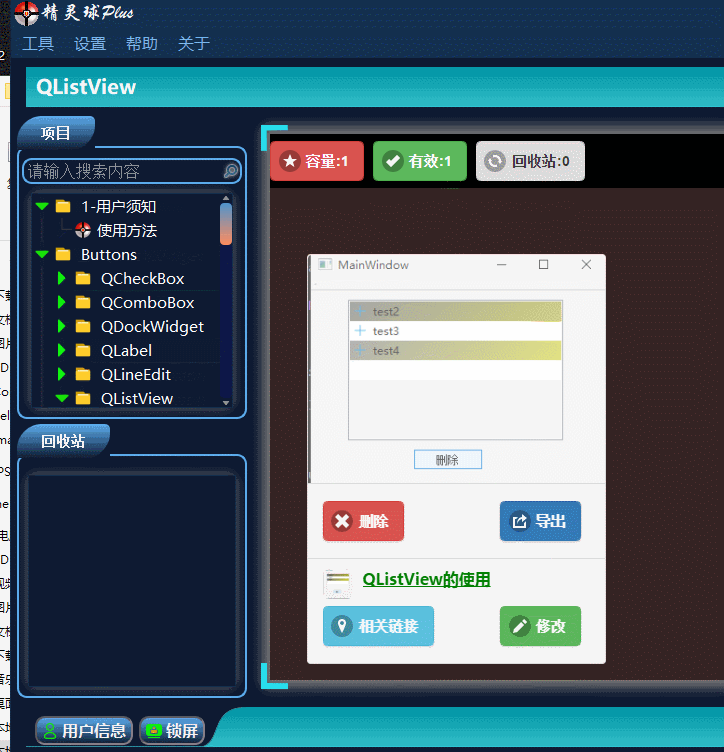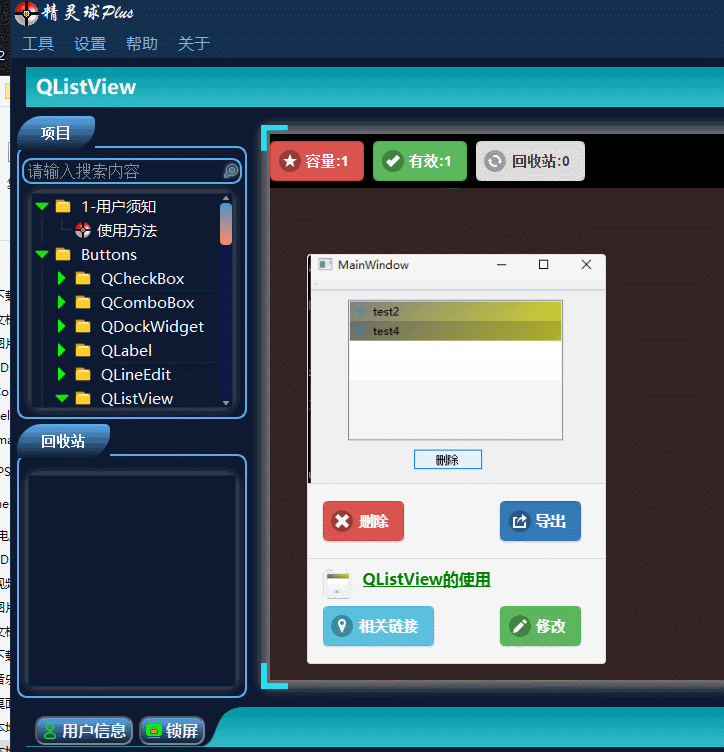
目录 一、QListView界面相关 1、布局介绍 二、代码展示 1、创建模型,导入模型 2、 设置隔行背景色 3、删除选中行 三、源码下载 此文为作者原创,创作不易,转载请标明出处! 一、QListView界面相关 1、布局介绍 先看下界面…...
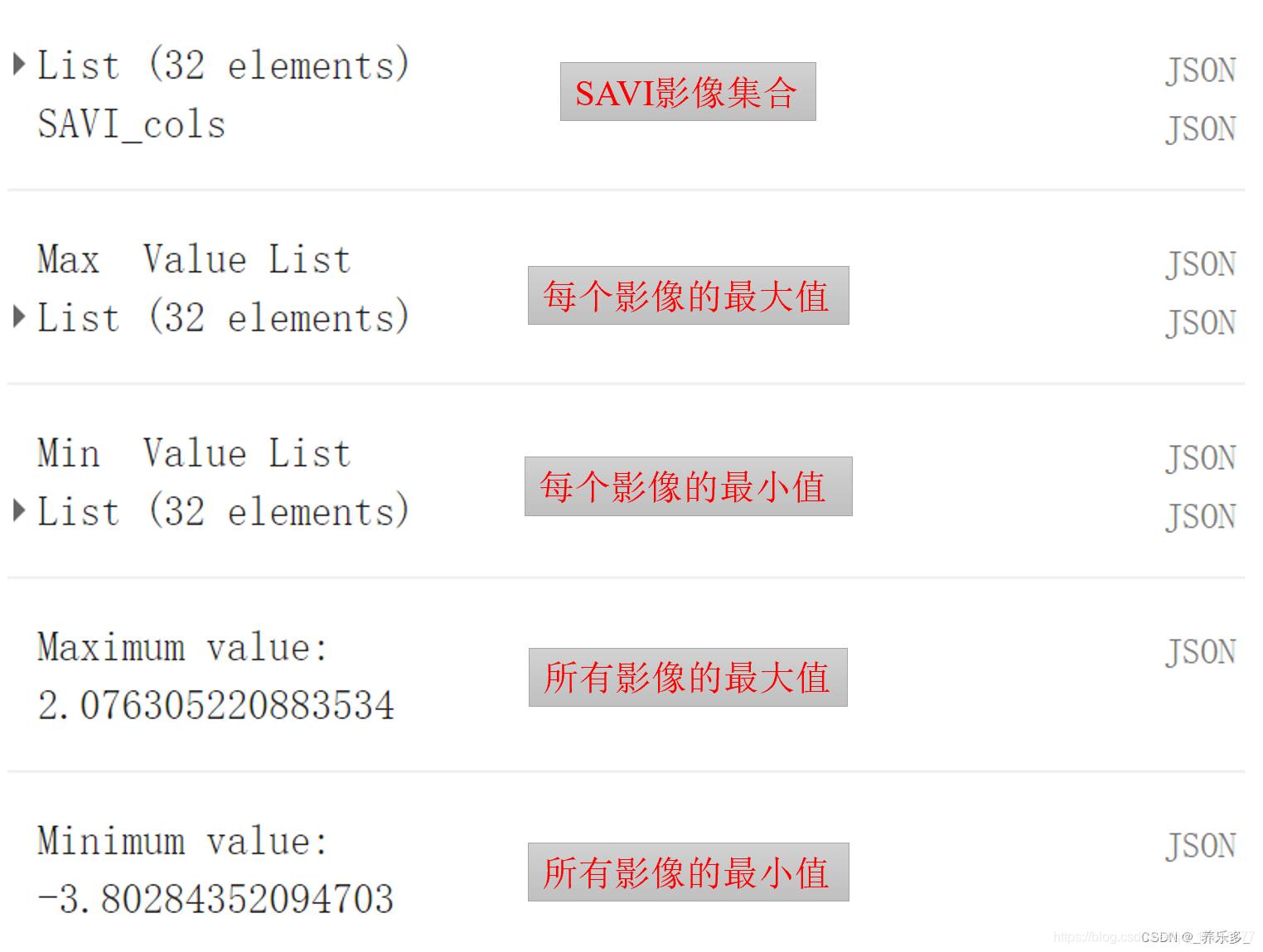
GEE:计算1990-2021年的指数最大值和最小值,并根据最大最小值对每一副影像归一化
本文记录了在GEE平台上计算影像集合中所有像素的最大值和最小值。并且根据该最大最小值对所有影像进行最大最小值归一化。以SAVI为例,记录了主要函数的使用方法和代码。 结果如图所示, 文章目录 一、计算每一副影像的最大值或者最小值,并将最值保存在 List 中二、计算 Lis…...

LeetCode KMP 算法
可以参考https://www.bilibili.com/video/BV1AY4y157yL/kmp 主要做的就是子串匹配,类似C程序的 strstr() 函数记录一下,也防止我自己忘记传统暴力求解算法是源串 ssssssssa 子串 sssa(下面暴力求解) 先 (子串从 0 位置匹配&#x…...

全面剖析OpenAI发布的GPT-4比其他GPT模型强在哪里
最强的文本生成模型GPT-4一、什么是GPT-4二、GPT-4的能力三、和其他GPT模型比较3.1、增加了图像模态的输入3.2、可操纵性更强3.3、复杂任务处理能力大幅提升3.4、幻觉、安全等局限性的改善3.6、风险和缓解措施改善更多安全特性3.7、可预测的扩展四、与之前 GPT 系列模型比较五、…...
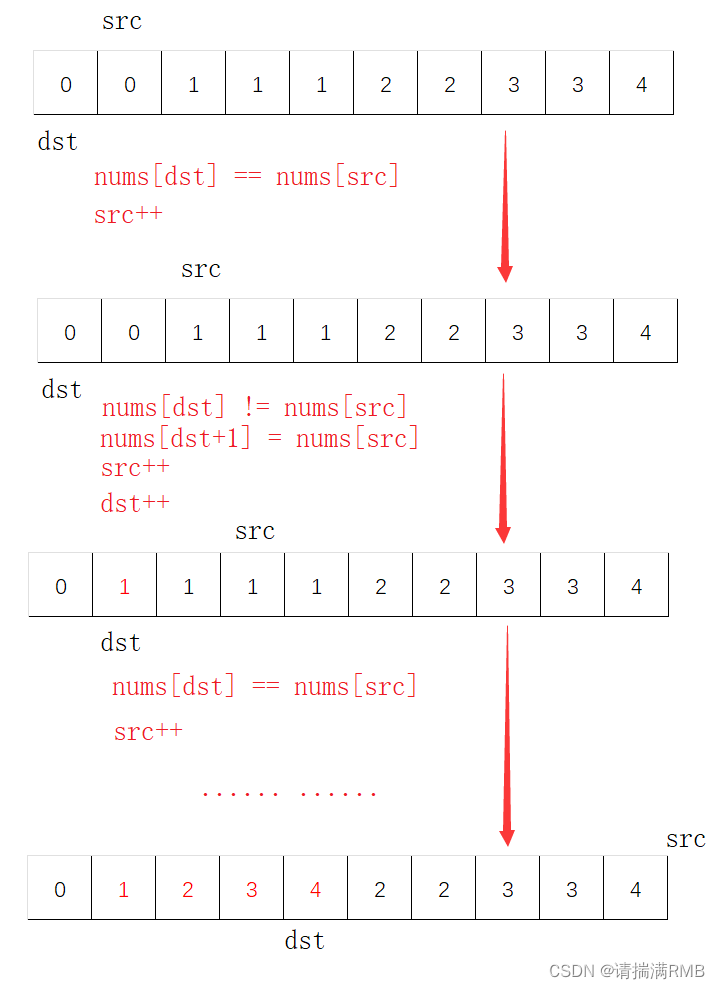
leetcode——26. 删除有序数组中的重复项
文章目录🐨1. 题目🏹2. 思路🪃3. 代码实现🐨1. 题目 给你一个升序排列的数组nums,请你原地删除重复出现的元素,使每个元素只出现一次,返回删除后数组的新长度。元素的相对顺序应该保持一致。 由…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
