WSL for Windows
1、安装
超详细Windows10/Windows11 子系统(WSL2)安装Ubuntu20.04(带桌面环境)_wsl安装ubuntu20.04-CSDN博客![]() https://blog.csdn.net/weixin_44301630/article/details/122390018
https://blog.csdn.net/weixin_44301630/article/details/122390018
注意,安装之后首次启动 Ubuntu 时,系统会提示你创建一个普通用户账户。使用此账户登录后,我们将设置 root 用户密码。
其他命令:
1、默认使用root角色运行
# 第一个是版本号-windows
ubuntu2204 config --default-user root查找版本号步骤,请看本子目录参考,里面由教程,这里需要注意的是有可能找不到ubuntu2204,这是因为没有添加到环境变量中,可下载一个everything进行查看。
运行相关的命令:
## 命令介绍-运行环境 ### 修改用户(root)密码-wsl
sudo passwd root# 切换用户(root)-wsl
su root# 查看wsl列表-windows
wsl -l# 使用指定用户(root)登录wsl(ubuntu,这个是由上面的`wsl -l`命令获取)-windows
wsl -d Ubuntu-22.04 -u root# 使用默认账户登录wsl-windows
bash / wsl# 关闭wsl-windows
wsl --shutdown参考:WINDOWS下的wsl如何设置Linux子系统默认用户为root - funkergx - 博客园 (cnblogs.com)
2、解决wsl: 检测到 localhost 代理配置,但未镜像到 WSL。NAT 模式下的 WSL 不支持 localhost 代理,clash的网络设置。
这个文件在
C:\Users\<UserName>\.wslconfig中。并添加下列代码,自行创建.wslconfig文件
[experimental]
autoMemoryReclaim=gradual # gradual | dropcache | disabled
networkingMode=mirrored
dnsTunneling=true
firewall=true
autoProxy=true参考Windows 11 + WSL + VS Code + Rust 环境配置 - LLW_NEU - 博客园 (cnblogs.com)
3、wsl使用docker for windows
首先下载docker desktop Docker: Accelerated Container Application Development
按照如下步骤设置:

就ok了,如果想要局域网互联,请参考:【WSL2】windows 安装适用于linux的子系统,安装 docker 并开启局域网访问!!_哔哩哔哩_bilibili
参考:
配置ssh:在 Windows 上通过 WSL 安装 Ubuntu 22.04 并配置 root 用户登录 (geeksuper.cn)
相关文章:

WSL for Windows
1、安装 超详细Windows10/Windows11 子系统(WSL2)安装Ubuntu20.04(带桌面环境)_wsl安装ubuntu20.04-CSDN博客https://blog.csdn.net/weixin_44301630/article/details/122390018 注意,安装之后首次启动 Ubuntu 时&…...

Matlab freqz 代码简单实现
相关代码打开matlab源码也可以看到,这里做了简单实现,与源码并不完全一样。 实现代码 [h2 w2] freqzfir(data); [h1 w1] freqz(data); h2h2; h12 [h1, h2];[h4 w4] freqziir(b,a, 2001,true); [h3 w3] freqz(b,a, w4, whole); h4 h4; h34 h…...
待办app哪款好?高效待办软件推荐
在快节奏的现代生活中,一款高效的待办事项管理软件对于提升工作效率和个人时间管理至关重要。面对市场上众多的待办app,哪款才是你的最佳选择呢?经过深入体验和对比,我发现敬业签这款高效待办软件是个不错的选择。 敬业签的快速记…...
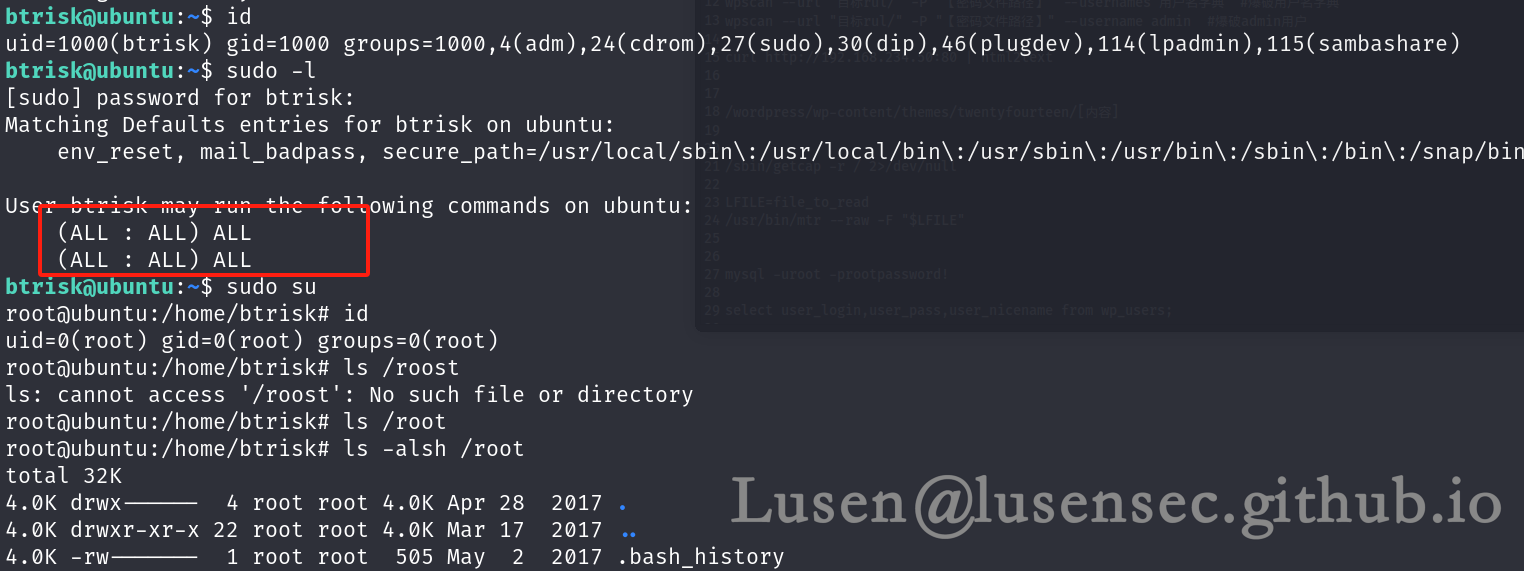
【OSCP系列】OSCP靶机-BTRsys-2.1(原创)
OSCP系列靶机—BTRsys-2.1 原文转载已经过授权 原文链接:Lusen的小窝 - 学无止尽,不进则退 (lusensec.github.io) 一、主机发现 二、端口扫描 1、快速扫描 2、全端口扫描 3、服务系统探测 4、漏洞探测 80端口扫到了一些目录,有wordpress框…...
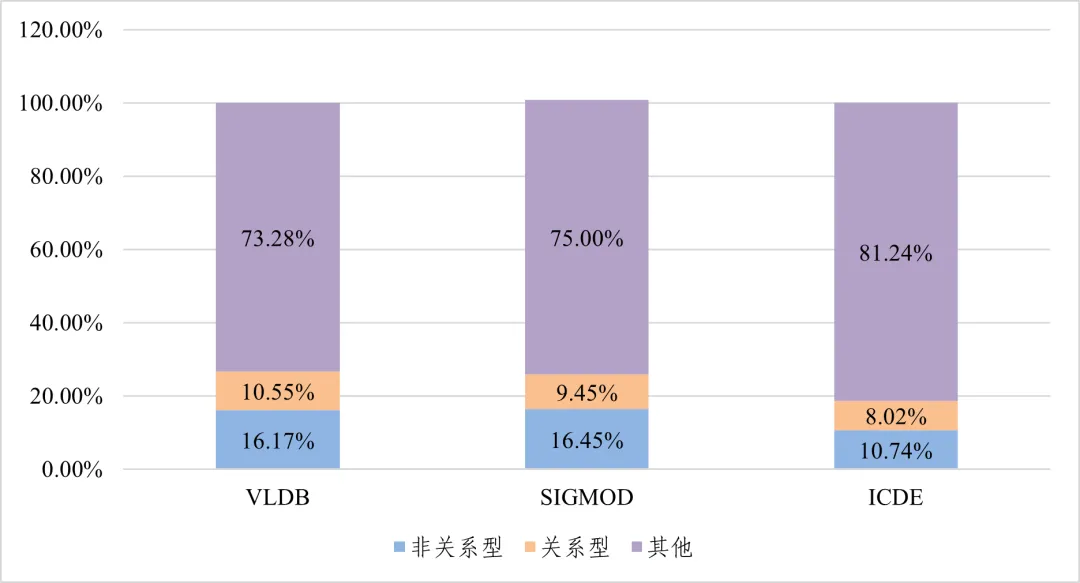
攻坚克难岁月长,自主腾飞世界强——回顾近代中国数据库的发展与飞跃
前言 最近看了《中国数据库前世今生》纪录片,感触颇深,也是一直在思考到底该用何种方式起笔来回顾这段筚路蓝缕却又充满民族自豪感的历程。大概构思了一周左右吧,我想,或许还是应该从那个计算机技术在国内刚刚萌芽的年代开始讲起…...

WEB前端12-axios基础
Vue2-axios基础 1.axios基本概念 在现代的前端开发中,处理网络请求是至关重要的一部分。Axios 是一个流行的基于 Promise 的 HTTP 客户端,它可以在浏览器和 Node.js 环境中使用。它的设计简单易用,支持并行请求、拦截器、CSRF 防护等特性&a…...

Ubuntu 防火墙设置
目录 1. 安装防火墙 2. 开启和关闭防火墙 3. 开放端口和服务规则 4. 关闭端口和删除服务规则 5. 查看防火墙状态 1. 安装防火墙 如果已经安装就忽略 # 安装ufw(Uncomplicated Firewall),这是Ubuntu上管理防火墙的一个简单工具 sudo ap…...
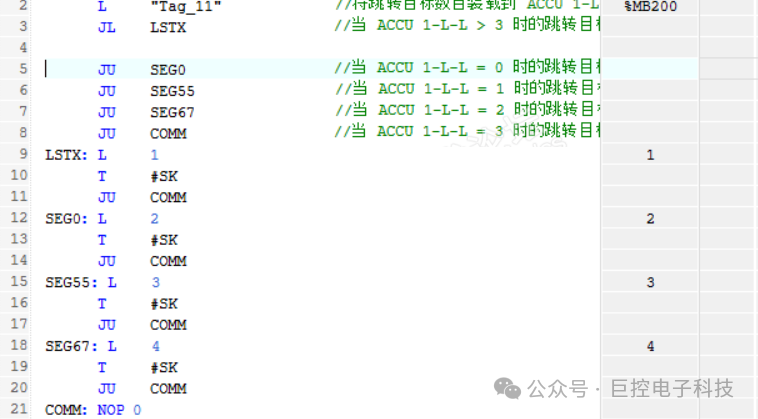
JL 跳转指令的理解
一般情况下,JU 和 JC 是最常见的跳转指令;但有时会用到JL 指令,JL 说起来更像是一组指令,类似C,C# 语言中的 switch case 语句,但是有个明显的不同,前者的判断条件可以是任意合理数字,后者范围…...

vue大屏展示组件库datav
主要用于构建大屏数据展示页面,具有多种类型组件可供使用。详情参考 datav官网 一、安装 npm 安装 npm install jiaminghi/data-viewyarn安装 yarn add jiaminghi/data-view二、使用 在main.js中注册为全局组件 import dataV from jiaminghi/data-view Vue.us…...
的集成应用)
Vue.js 与 Ajax(vue-resource)的集成应用
Vue.js 与 Ajax(vue-resource)的集成应用 Vue.js 是一款流行的前端JavaScript框架,以其简洁、灵活和高效的特点而受到开发者的喜爱。在实际开发中,与后端服务的通信是不可或缺的,而Ajax技术是实现这一功能的关键。在V…...

【讲解下AI Native应用中的模型微调】
🌈个人主页: 程序员不想敲代码啊 🏆CSDN优质创作者,CSDN实力新星,CSDN博客专家 👍点赞⭐评论⭐收藏 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共…...

【SOC 芯片设计 DFT 学习专栏 -- DFT DRC规则检查】
请阅读【嵌入式及芯片开发学必备专栏】 请阅读【芯片设计 DFT 学习系列 】 如有侵权,请联系删除 转自: 芯爵ChipLord 2024年07月10日 12:00 浙江 文章目录 概述DRC的概念Tessent DRC检查的概述时钟相关检查扫描相关检查BIST规则检查预DFT时钟规则检查 …...

深度学习:如何计算感受野
感受野(Receptive Field)是卷积神经网络(CNN)中的一个重要概念,用于描述输入图像中的一个像素在输出特征图中影响的区域大小。在设计和理解卷积神经网络时,计算感受野有助于理解网络如何对输入数据进行处理…...

【状语从句】
框架 概念,特点主将从现连接词时间条件地点结果方式让步原因目的比较省略倒装 解读 1【概念,特点】 一个完整的句子,去修饰另一个完整句子中的动词,称为状语从句;特点:从句完整,只用考虑连接词是…...

阿里云服务器安装Anaconda后无法检测到
前言 问题如标题所言,就是conda -V验证错误,不过后来发现其实就是虽然安装时,同意了写入环境变量,但是其实还没有写入,需要手动写入。下面也会重复一遍安装流程。 安装 到[Anaconda下载处](Download Now | Anaconda)查…...

在没有源程序的情况时,如何通过控制鼠标按钮控制电脑exe程序?
有时候想控制第三方软件,但是没有源程序,可以控制鼠标键盘自动操作软件达到我们想要的目的 首先建一个功能类包含窗口控制,鼠标控制和输入控制等 csharp using System; using System.Collections.Generic; using System.Linq; using System.…...

如何排查GD32 MCU复位是由哪个复位源导致的?
上期为大家讲解了GD32 MCU复位包括电源复位和系统复位,其中系统复位还包括独立看门狗复位、内核软复位、窗口看门狗复位等,在一个GD32系统中,如果莫名其妙产生了MCU复位,如何排查具体是由哪个复位源导致的呢? GD32 MC…...
)
【C算法】编程初学者入门训练140道(1~20)
牛客编程初学者入门训练150题 BC1 实践出真知BC2 我是大VBC3 有容乃大BC6 小飞机BC7 缩短二进制BC8 十六进制转十进制BC9 printf的返回值BC10 成绩输入输出BC11 学生基本信息输入输出BC12 字符圣诞数BC13 ASCII 码BC14 出生日期输入输出BC15 按照格式输入并交换输出BC16 字符转…...

消息队列-rabbitmq(生产者.消费者. 消息.可靠性)
生产者者的可靠性 为了保证我们生产者在发送消息的时候消息不丢失,我们需要保证发送者的可靠性 1.生产者重试 假如发送消息的时候消息丢失 ,我们可以使用发送者 重试机制,尝试重新发送消息 实现该机制非常简单,只需要在yml文…...

《InheriBT行为树》For Unity
InheriBT: Unity Editor中的行为树编辑框架 行为树(Behavior Tree)是一种广泛应用于人工智能(AI)领域的决策模型,特别是在游戏开发中。行为树通过分层结构和节点的组合,实现了复杂行为的简洁表达。然而&am…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...

在Zenodo下载文件 用到googlecolab googledrive
方法:Figshare/Zenodo上的数据/文件下载不下来?尝试利用Google Colab :https://zhuanlan.zhihu.com/p/1898503078782674027 参考: 通过Colab&谷歌云下载Figshare数据,超级实用!!࿰…...
