动态规划-基础(斐波那契数、爬楼梯、使用最小花费爬楼梯、不同路径、不同路径II、整数拆分、不同的二叉搜索树)
动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。所以动态规划中每一个状态一定是由上一个状态推导出来的。
动态规划问题,五步走:
状态定义:确定 dp 数组,下标及其含义
状态转移:
初始化:
遍历顺序:
返回值:
动态规划代码有问题分析
举例推导状态转移公式
打印 dp 数组日志
1.斐波那契数
题目链接:509. 斐波那契数 - 力扣(LeetCode)
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2
输出:1
解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3
输出:2
解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:n = 4
输出:3
解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
代码:
/**1. 状态定义:dp[i]为斐波那契数列的自变量i,dp[i] = F(i)2. 状态转移:dp[i] = dp[i-1] + dp[i-2]3. 初始化:dp[0] = 0, dp[1] = 14. 遍历顺序:正序5. 返回形式:dp[n]*/public int fib(int n) {if(n == 0 || n == 1) {return n;}int a = 0, b = 1,sum = 0;for(int i = 2; i <= n; i++) {sum = a + b;a = b;b = sum;}return sum;}2. 爬楼梯
题目链接:70. 爬楼梯 - 力扣(LeetCode)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
1 阶 + 1 阶
2 阶
示例 2:
输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
1 阶 + 1 阶 + 1 阶
1 阶 + 2 阶
2 阶 + 1 阶
提示:
1 <= n <= 45
思路:

代码:
/**1. 状态定义:到达第 i 个台阶,有 dp[i] 中方法2. 状态转移:dp[i] = dp[i-1] + dp[i-2]3. 初始化:dp[1] = 1 dp[2] = 2 注意题中要求 n != 04. 遍历顺序:从前往后5. 返回值:返回 dp[n]*/public int climbStairs(int n) {if(n < 2) return n;int[] dp = new int[n+1];dp[1] = 1;dp[2] = 2;for(int i = 3; i <= n; i++) {dp[i] = dp[i-2] + dp[i-1];}return dp[n];}3. 使用最小花费爬楼梯
题目链接:使用最小花费爬楼梯
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
示例 1:
输入:cost = [10,15,20]
输出:15
解释:你将从下标为 1 的台阶开始。
支付 15 ,向上爬两个台阶,到达楼梯顶部。
总花费为 15 。
示例 2:
输入:cost = [1,100,1,1,1,100,1,1,100,1]
输出:6
解释:你将从下标为 0 的台阶开始。
支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。
支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。
支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。
支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。
支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。
支付 1 ,向上爬一个台阶,到达楼梯顶部。
总花费为 6 。
提示:
2 <= cost.length <= 1000
0 <= cost[i] <= 999
思路:

代码:
/**1. 状态定义:到达 i 位置最小花费 dp[i]2. 状态转移:dp[i] = min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2])3. 初始化:dp[0] = 0, dp[1] = 0 前两个台阶是直接到达的,不花费4. 遍历顺序:从前往后5. 返回值:dp[cost.length]*/public int minCostClimbingStairs(int[] cost) {int len = cost.length;int[] dp = new int[len + 1];dp[0] = 0;dp[1] = 0;for(int i = 2; i <= len; i++) {dp[i] = Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[len];}4. 不同路径
题目链接:62. 不同路径 - 力扣(LeetCode)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:

输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
向右 -> 向下 -> 向下
向下 -> 向下 -> 向右
向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 109
思路:

代码:
/**1. 状态定义:dp[i][j] 表示从 (0,0) 到 ()2. 状态转移:dp[i][j] = dp[i-1][j] + dp[i][j-1]3. 初始化: 行:dp[0][j] = 1, 列:dp[i][0] = 14. 遍历顺序:从左到右,从上到下5. 返回值:dp[m][n]*/
public int uniquePaths(int m, int n) {int[][] dp = new int[m][n];// 初始化for(int i = 0; i < m; i++) {dp[i][0] = 1;}for(int j = 0; j < n; j++) {dp[0][j] = 1;}// 遍历打印for(int i = 1; i < m; i++) {for(int j = 1; j < n; j++) {dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[m-1][n-1];
}5. 不同路径 II
题目链接:63. 不同路径 II - 力扣(LeetCode)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:
输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
向右 -> 向右 -> 向下 -> 向下
向下 -> 向下 -> 向右 -> 向右
示例 2:
输入:obstacleGrid = [[0,1],[0,0]]
输出:1
提示:
m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1
思路:
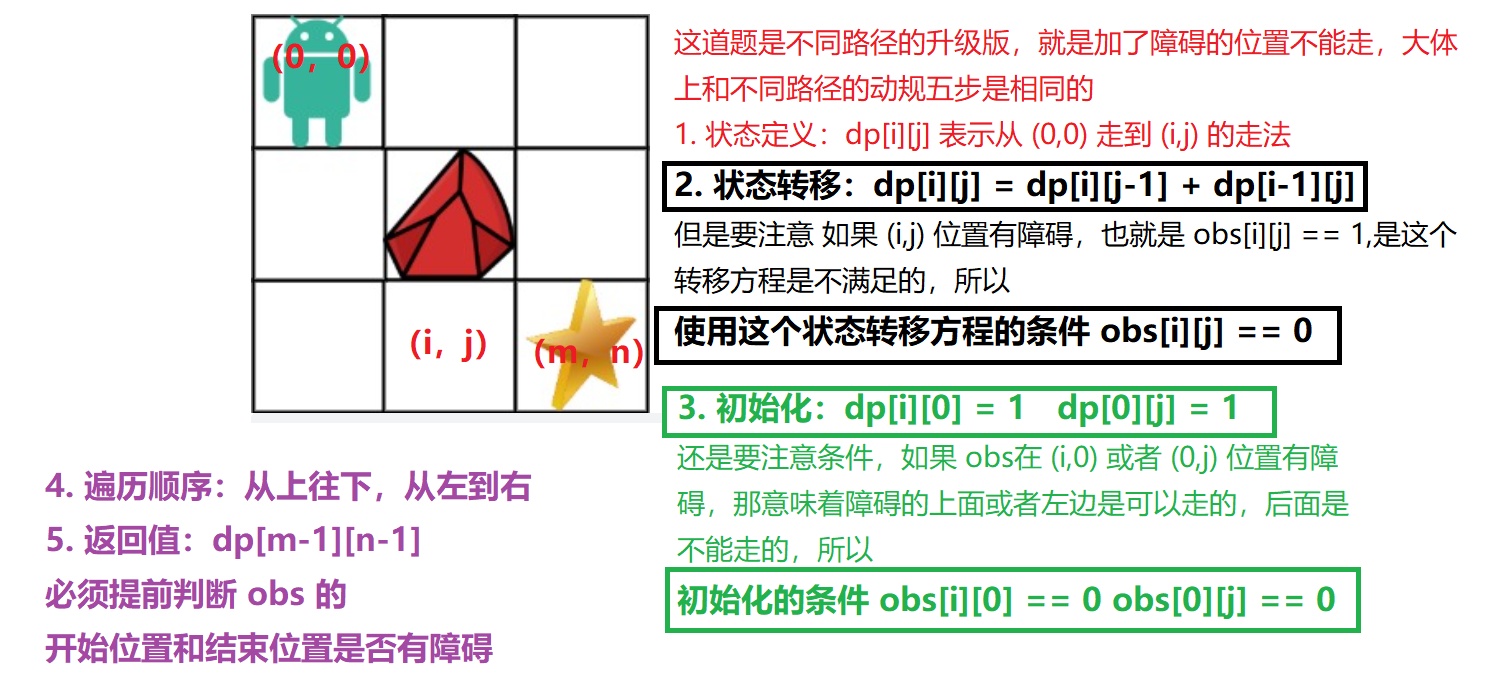
代码:
/**1. 状态定义: dp[i][j] 表示到达 (i,j) 位置有多少种走法2. 状态转移:条件:obs[i][j] = 0 时才有这个方程,表示这个位置没有障碍物dp[i][j] = dp[i-1][j] + dp[i][j-1] 3. 初始化:条件:当 obs[i][0] = 0 时,才有 dp[i][0] = 1当 obs[0][j] = 0 时,才有 dp[0][j] = 1 4. 遍历顺序:从上到下,从左到右5. 返回值:当初始位置或结束位置 obs 为 1 时,表示有障碍,直接返回 0,正常情况下返回 dp[m][n]*/public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length; // 行int n = obstacleGrid[0].length; // 列if(obstacleGrid[0][0] == 1 || obstacleGrid[m-1][n-1] == 1) {return 0;}int[][] dp = new int[m][n];// 初始化for(int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {dp[i][0] = 1;}for(int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {dp[0][j] = 1;}for(int i = 1; i < m; i++) {for(int j = 1; j < n; j++) {if(obstacleGrid[i][j] == 0) {dp[i][j] = dp[i-1][j] + dp[i][j-1];}}}return dp[m-1][n-1];}6. 整数拆分
题目链接:343. 整数拆分 - 力扣(LeetCode)
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
提示:
2 <= n <= 58
思路:

代码:
/**1. 状态定义:对 i 进行拆分,得到最大的积为 dp[i]2. 状态转移:dp[i] = Math.max(dp[i], Math.max(j*(i-j), j * dp[i-j]));3. 初始化:dp[0] = 0,dp[1] = 0,dp[2] = 24. 遍历顺序:从前向后5. 返回值:dp[n]*/public int integerBreak(int n) {int[] dp = new int[n+1];dp[2] = 1;for(int i = 3; i <= n; i++) {for(int j = 1; j <= i-j; j++) {dp[i] = Math.max(dp[i],Math.max(j*(i-j), j*dp[i-j]));}}return dp[n];}7. 不同的二叉搜索树
题目链接:96. 不同的二叉搜索树 - 力扣(LeetCode)
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
输入:n = 3
输出:5
示例 2:
输入:n = 1
输出:1
提示:
1 <= n <= 19
思路:
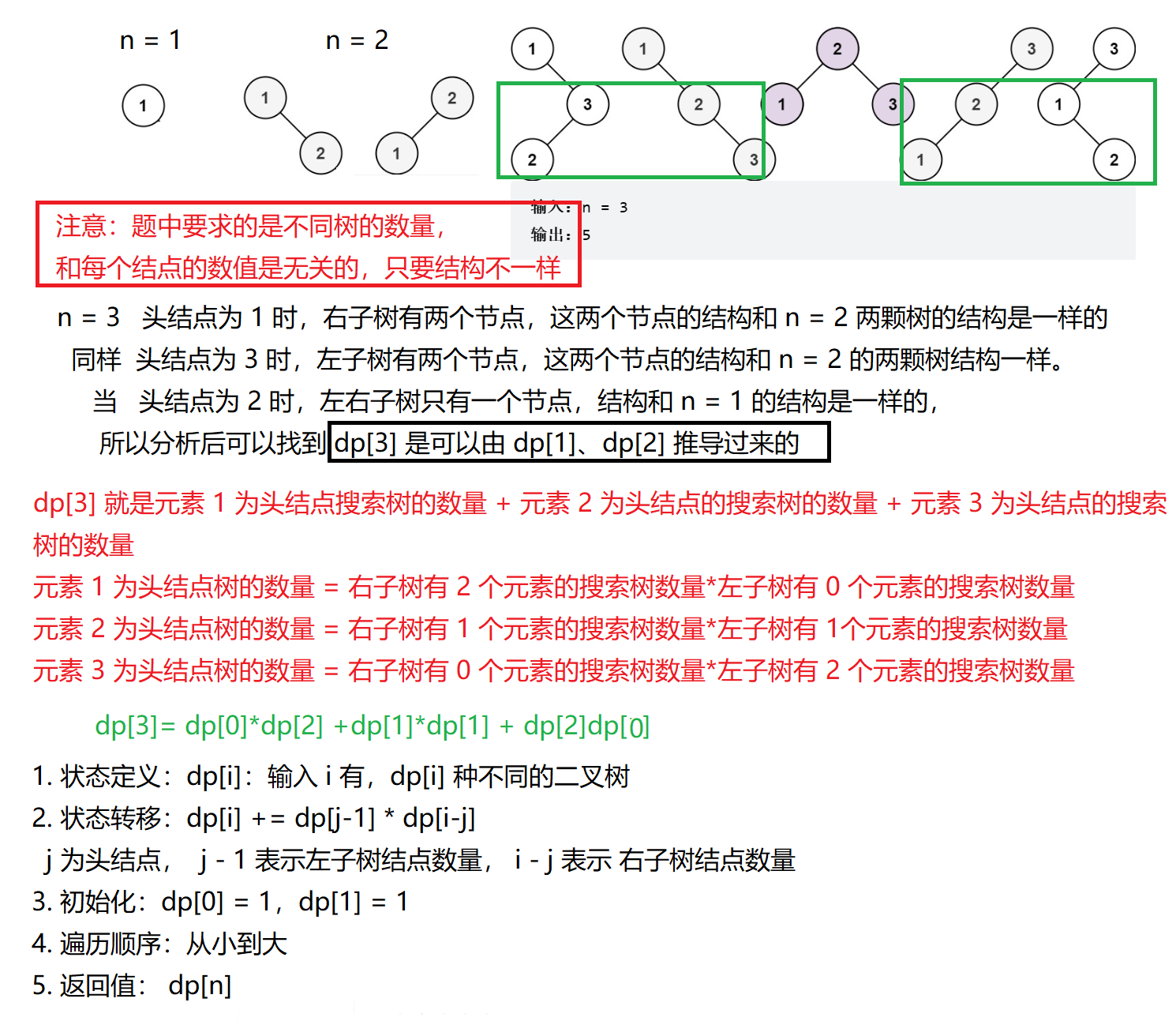
代码:
/**1. 状态定义:dp[i] 表示输入 i,有 dp[i] 种不同的二叉搜索树2. 状态转移:dp[i] += dp[j-1]*dp[i-j]3. 初始化:dp[0] = 1, dp[1] = 14. 遍历顺序:从小到大5. 返回值:dp[n]
*/
public int numTrees(int n) {int[] dp = new int[n+1];dp[0] = 1;dp[1] = 1;for(int i = 2; i <= n; i++) {for(int j = 1; j <= i; j++) {dp[i] += dp[j-1]*dp[i-j];}}return dp[n];
}2. 背包问题相关文章:

动态规划-基础(斐波那契数、爬楼梯、使用最小花费爬楼梯、不同路径、不同路径II、整数拆分、不同的二叉搜索树)
动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。所以动态规划中每一个状态一定是由上一个状态推导出来的。动态规划问题,五步走:状态定义&am…...
深入理解WebSocket协议
“ 一直以来对WebSocket仅停留在使用阶段,也没有深入理解其背后的原理。当看到 x x x was not upgraded to websocket,我是彻底蒙了,等我镇定下来,打开百度输入这行报错信息,随即看到的就是大家说的跨域,或…...
Vector的扩容机制
到需要扩容的时候,Vector会根据需要的大小,创建一个新数组,然后把旧数组的元素复制进新数组。 我们可以看到,扩容后,其实是一个新数组,内部元素的地址已经改变了。所以扩容之后,原先的迭代器会…...
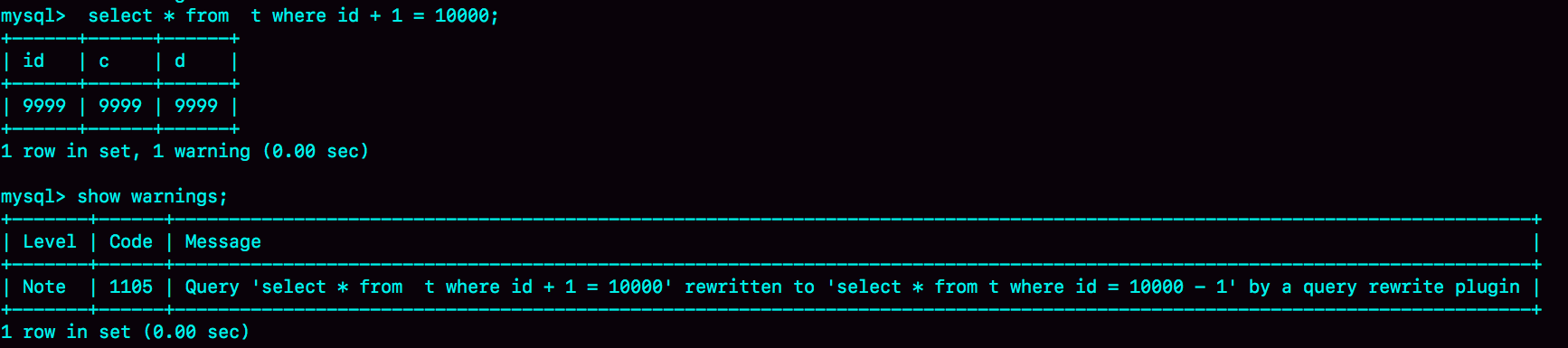
22讲MySQL有哪些“饮鸩止渴”提高性能的方法
短连接风暴 是指数据库有很多链接之后只执行了几个语句就断开的客户端,然后我们知道数据库客户端和数据库每次连接不仅需要tcp的三次握手,而且还有mysql的鉴权操作都要占用很多服务器的资源。话虽如此但是如果连接的不多的话其实这点资源无所谓的。 但是…...
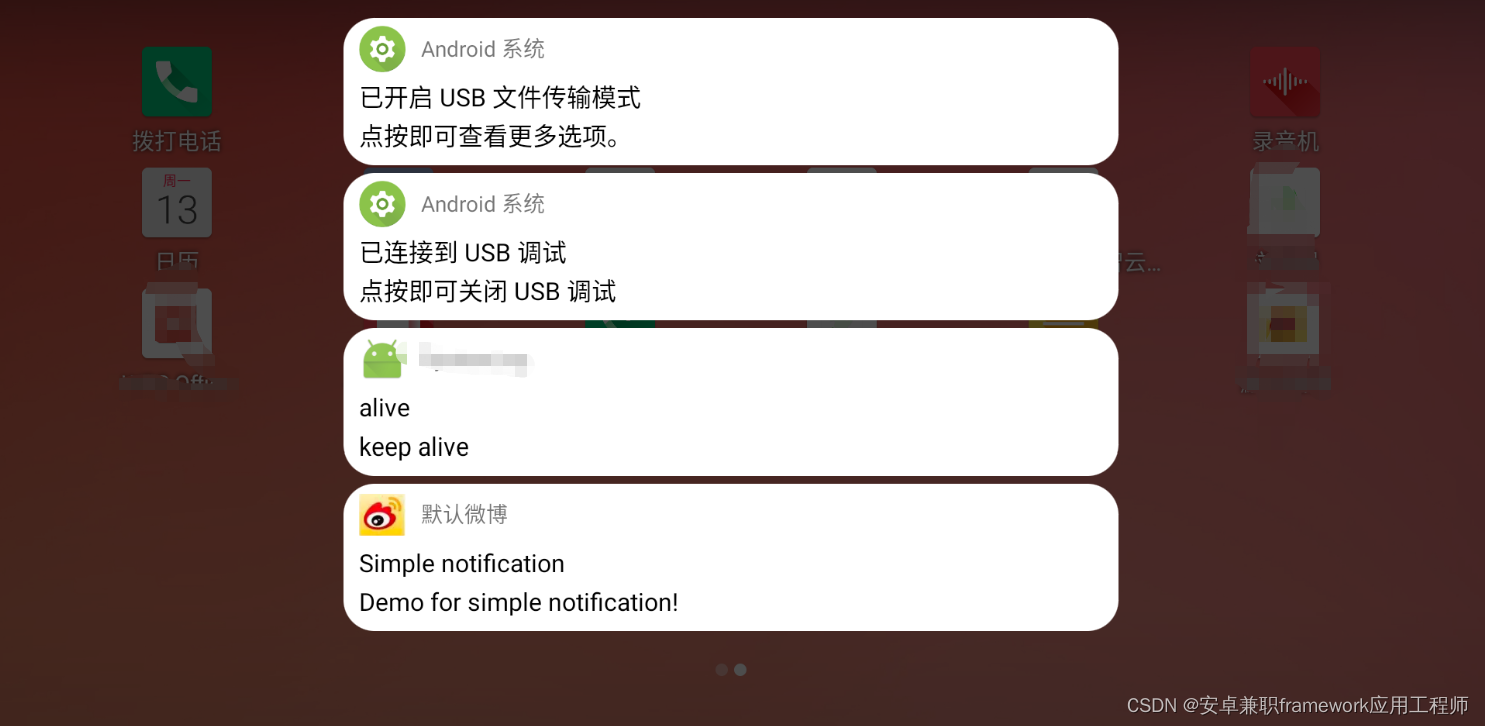
10.0自定义SystemUI下拉状态栏和通知栏视图(六)之监听系统通知
1.前言 在进行rom产品定制化开发中,在10.0中针对systemui下拉状态栏和通知栏的定制UI的工作开发中,原生系统的下拉状态栏和通知栏的视图UI在产品开发中会不太满足功能, 所以根据产品需要来自定义SystemUI的下拉状态栏和通知栏功能,首选实现的就是下拉通知栏左滑删除通知的部…...
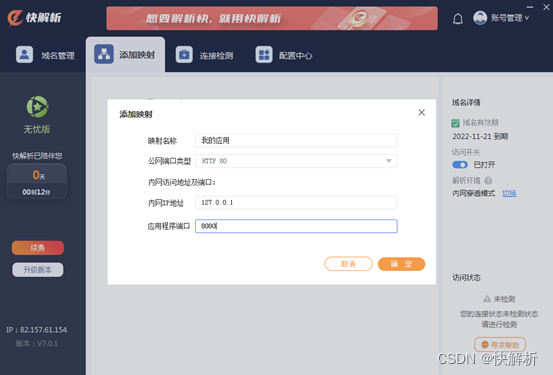
怎样在外网登录访问CRM管理系统?
一、什么是CRM管理系统? Customer Relationship Management,简称CRM,指客户关系管理,是企业利用信息互联网技术,协调企业、顾客和服务上的交互,提升管理服务。为了企业信息安全以及使用方便,企…...
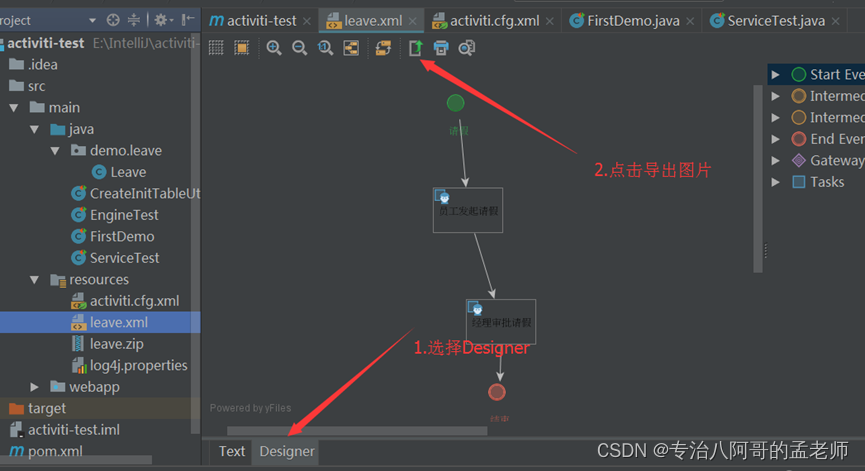
Activity工作流(三):Service服务
3. Service服务 所有的Service都通过流程引擎获得。 3.1 RepositoryService 仓库服务是存储相关的服务,一般用来部署流程文件,获取流程文件(bpmn和图片),查询流程定义信息等操作,是引擎中的一个重要的服务。…...

算法--最长回文子串--java--python
这个算法题里面总是有 暴力解法 把所有字串都拿出来判断一下 这里有小小的优化: 就是当判断的字串小于等于我们自己求得的最长回文子串的长度,那么我们就不需要在进行对这个的判断这里的begin,还可以用来取得最小回文子串是什么 java // 暴…...
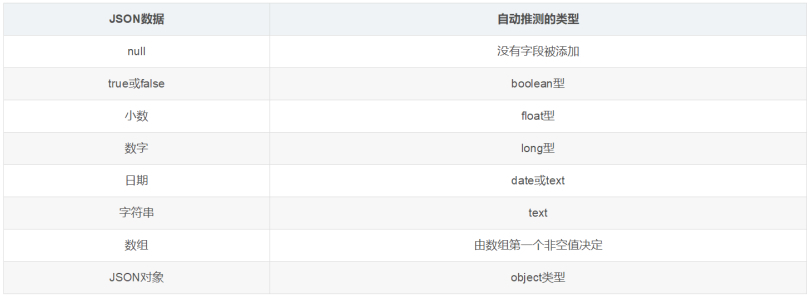
ElasticSearch-第二天
目录 文档批量操作 批量获取文档数据 批量操作文档数据 DSL语言高级查询 DSL概述 无查询条件 叶子条件查询 模糊匹配 match的复杂用法 精确匹配 组合条件查询(多条件查询) 连接查询(多文档合并查询) 查询DSL和过滤DSL 区别 query DSL filter DSL Query方式查…...
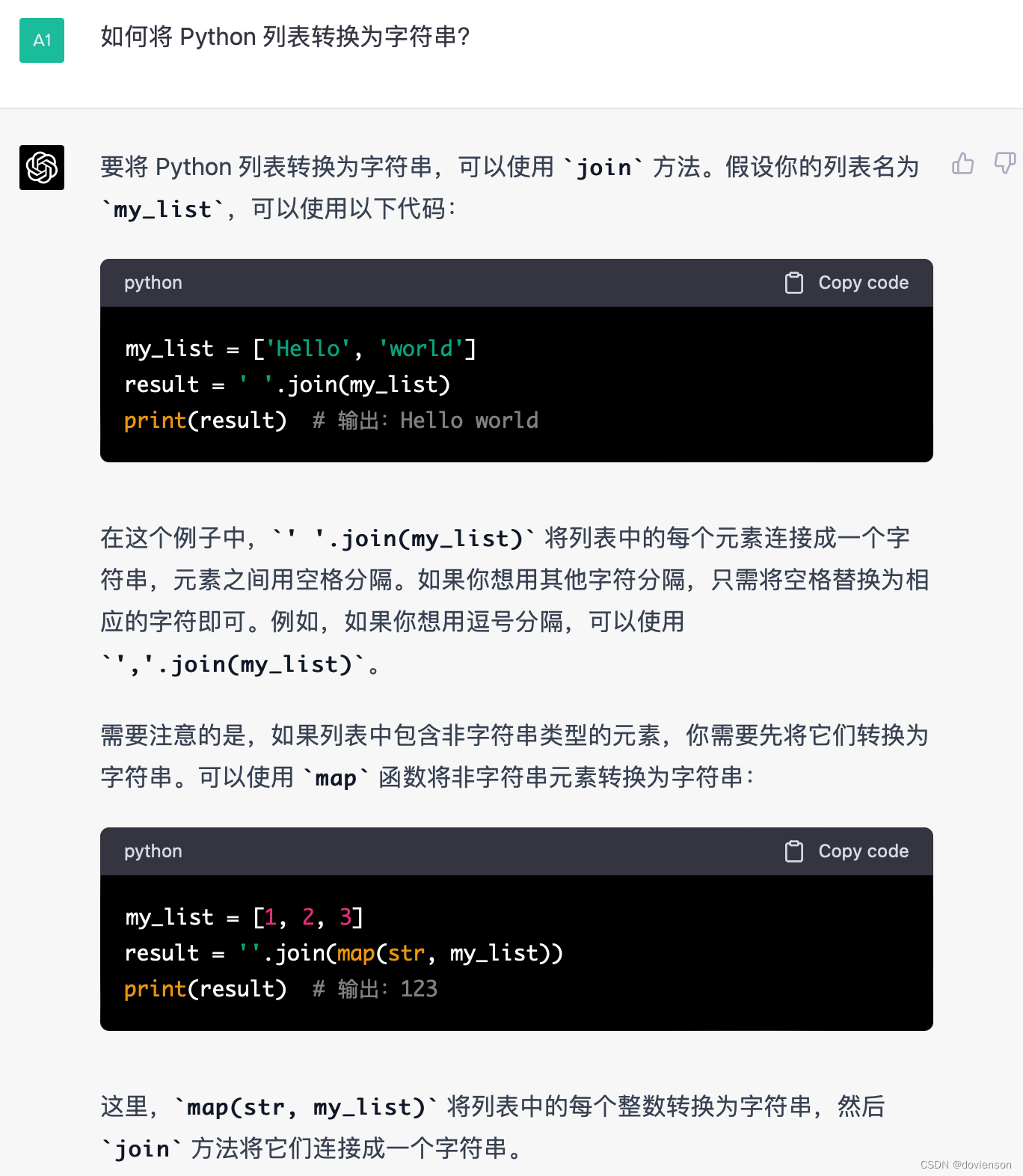
【AI大比拼】文心一言 VS ChatGPT-4
摘要:本文将对比分析两款知名的 AI 对话引擎:文心一言和 OpenAI 的 ChatGPT,通过实际案例让大家对这两款对话引擎有更深入的了解,以便大家选择合适的 AI 对话引擎。 亲爱的 CSDN 朋友们,大家好!近年来&…...

美团笔试-3.18
1、捕获敌人 小美在玩一项游戏。该游戏的目标是尽可能抓获敌人。 敌人的位置将被一个二维坐标 (x, y) 所描述。 小美有一个全屏技能,该技能能一次性将若干敌人一次性捕获。 捕获的敌人之间的横坐标的最大差值不能大于A,纵坐标的最大差值不能大于B。 现在…...

【12】SCI易中期刊推荐——计算机信息系统(中科院4区)
🚀🚀🚀NEW!!!SCI易中期刊推荐栏目来啦 ~ 📚🍀 SCI即《科学引文索引》(Science Citation Index, SCI),是1961年由美国科学信息研究所(Institute for Scientific Information, ISI)创办的文献检索工具,创始人是美国著名情报专家尤金加菲尔德(Eugene Garfield…...

好不容易约来了一位程序员来面试,结果人家不做笔试题
感觉以后还是不要出面试题这环节好了。好不容易约来了一位程序员来面试。刚递给他一份笔试题,他一看到要做笔试题,说不做笔试题,有问题面谈就好了,搞得我有点尴尬,这位应聘者有3年多工作经验。关于程序员岗位ÿ…...

这几个过时Java技术不要再学了
Java 已经发展了近20年,极其丰富的周边框架打造了一个繁荣稳固的生态圈。 Java现在不仅仅是一门语言,而且还是一整个生态体系,实在是太庞大了,从诞生到现在,有无数的技术在不断的推出,也有很多技术在不断的…...

EEPROM芯片(24c02)使用详解(I2C通信时序分析、操作源码分析、原理图分析)
1、前言 (1)本文主要是通过24c02芯片来讲解I2C接口的EEPROM操作方法,包含底层时序和读写的代码; (2)大部分代码是EEPROM芯片通用的,但是其中关于某些时间的要求,是和具体芯片相关的,和主控芯片和外设芯片都有关系&…...
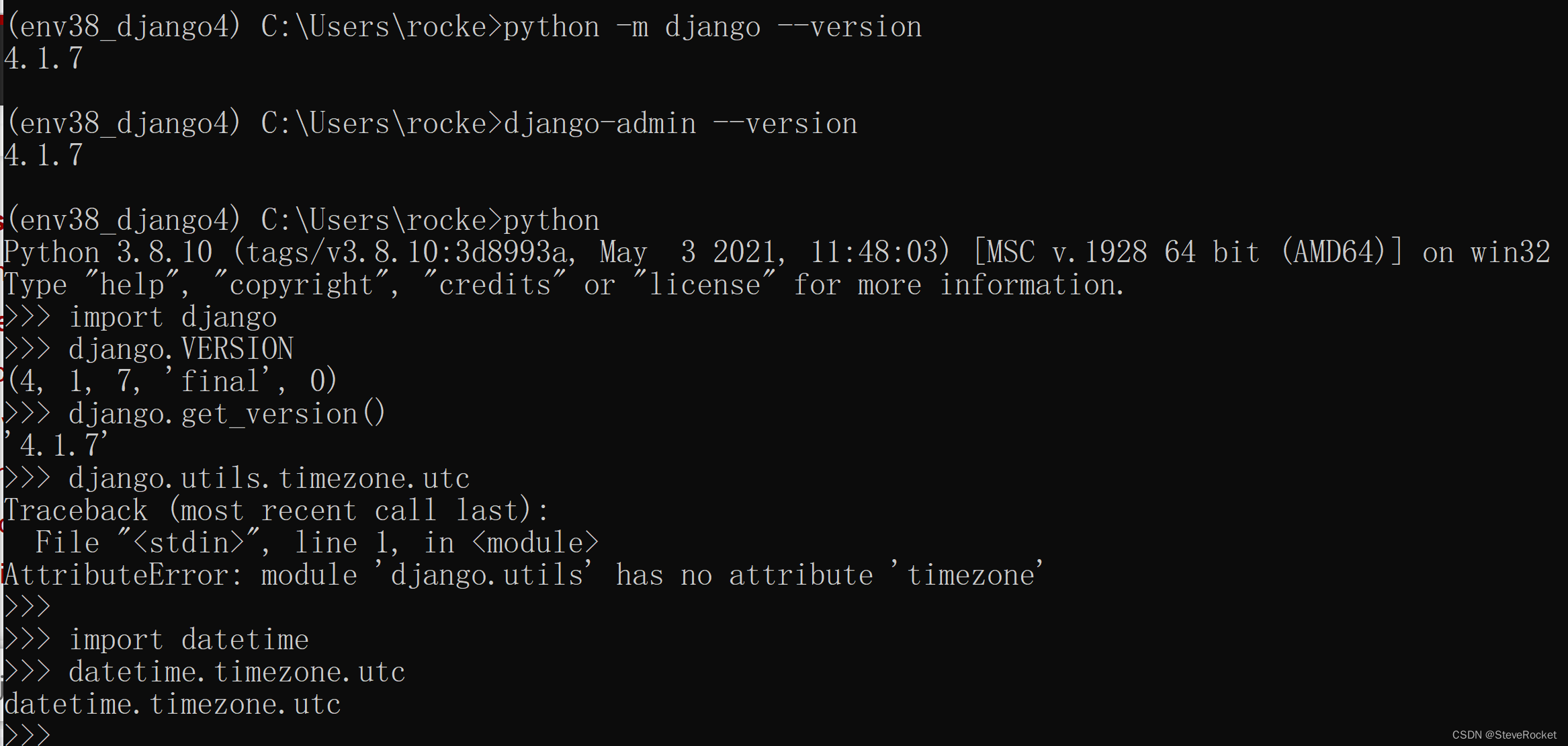
Django4.0新特性-主要变化
Django 4.0于2021年12月正式发布,标志着Django 4.X时代的来临。参考Django 4.0 release notes | Django documentation | Django Python 兼容性 Django 4.0 将支持 Python 3.8、3.9 与 3.10。强烈推荐并且仅官方支持每个系列的最新版本。 Django 3.2.x 系列是最后…...

MySQL高级面试题整理
1. 执行流程 mysql客户端先与服务器建立连接Sql语句通过解析器形成解析树再通过预处理器形成新解析树,检查解析树是否合法通过查询优化器将其转换成执行计划,优化器找到最适合的执行计划执行器执行sql 2. MYISAM和InNoDB的区别 MYISAM:不支…...

【Java】面向对象三大基本特征
【Java】面向对象三大基本特征 1.封装 On Java 8:研发程序员开发一个工具类,该工具类仅向应用程序员公开必要的内容,并隐藏内部实现的细节。这样可以有效地避免该工具类被错误的使用和更改,从而减少程序出错的可能。彼此职责划分清晰&#x…...
蓝桥杯C++组怒刷50道真题(填空题)
🌼深夜伤感网抑云 - 南辰Music/御小兮 - 单曲 - 网易云音乐 🌼多年后再见你 - 乔洋/周林枫 - 单曲 - 网易云音乐 18~22年真题,50题才停更,课业繁忙,有空就更,2023/3/18/23:01写下 目录 👊填…...

Shell自动化管理 for ORACLE DBA
1.自动收集每天早上9点到晚上8点之间的AWR报告。 auto_awr.sh #!/bin/bash# Set variables ORACLE_HOME/u01/app/oracle/product/12.1.0/dbhome_1 ORACLE_SIDorcl AWR_DIR/home/oracle/AWR# Set date format for file naming DATE$(date %Y%m%d%H%M%S)# Check current time - …...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...
