数据结构 | 栈的中缀表达式求值
目录
什么是栈?
栈的基本操作
入栈操作
出栈操作
取栈顶元素
中缀表达式求值
实现思路
具体代码
什么是栈?
栈是一种线性数据结构,具有“先进后出”(Last In First Out, LIFO)的特点。它可以看作是一种受限的线性表,只能在表的一端进行插入和删除操作,这一端被称为栈顶,另一端被称为栈底。不含任何元素的栈称为空栈。
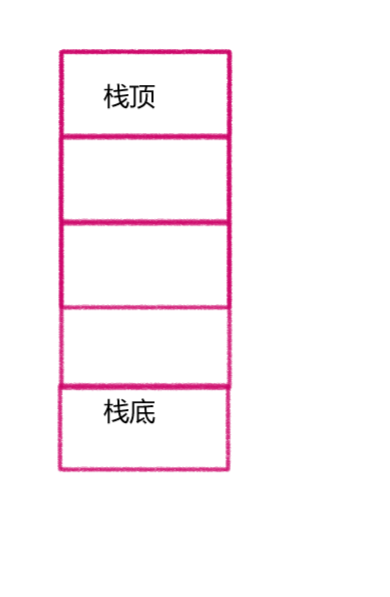
栈的基本操作包括:入栈、出栈、取栈顶元素等。
栈的基本操作
- 理解栈的基本原理和操作;
- 掌握栈在表达式求值中的应用。
入栈操作
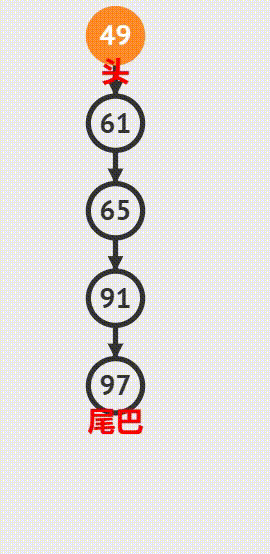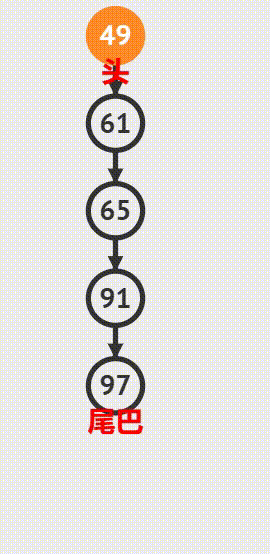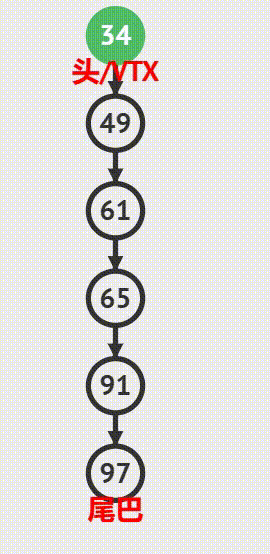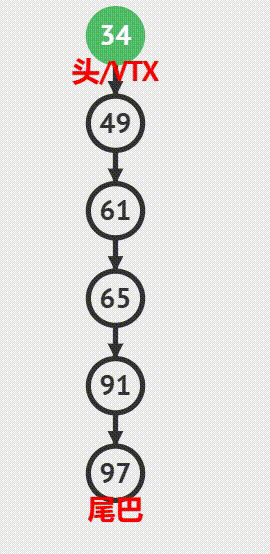
出栈操作
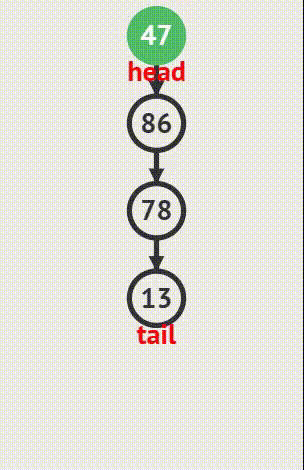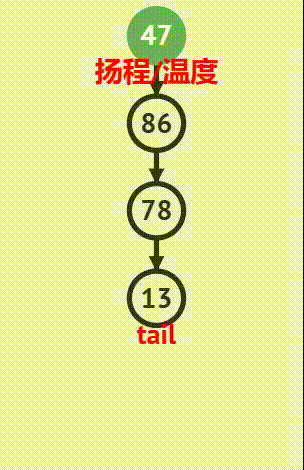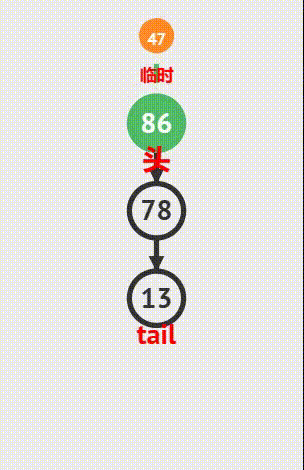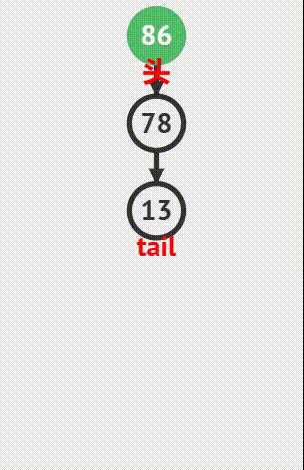
取栈顶元素
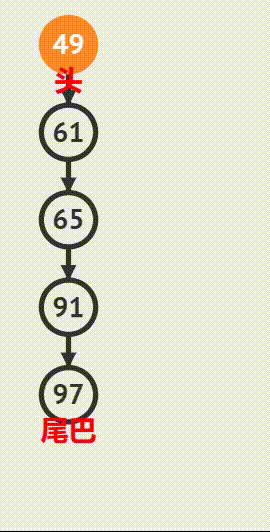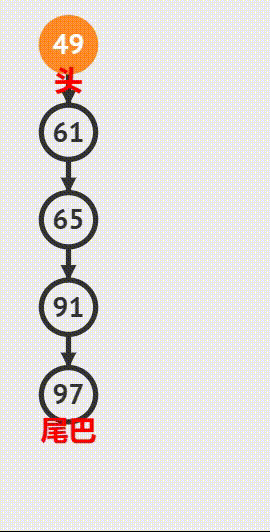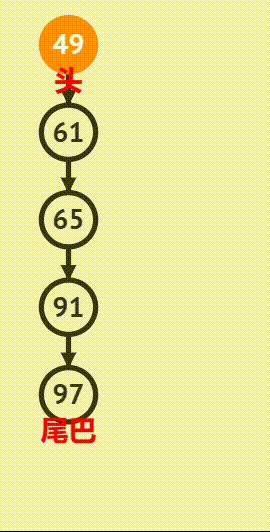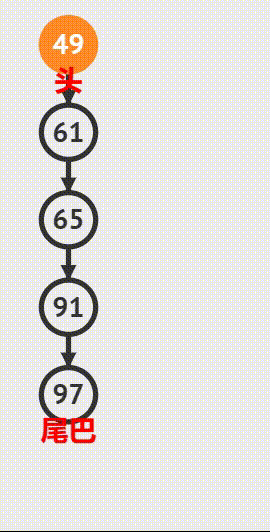
中缀表达式求值
中缀表达式是最常见的表达式表示方式,其表示形式为“操作数1 操作符 操作数2”。例如:
3+4同样表示加法运算,参数分别为3和4,其结果为7。
对于表达式求值,我们通常使用中缀表达式,需要转换为前缀或后缀表达式。转换完成后,可以直接使用栈来求解表达式的值。
实现思路
中缀表达式求值比较复杂,需要考虑运算符的优先级以及括号的影响。因此,我们一般使用栈来实现算法。
具体实现过程如下:
- 初始化两个栈:运算符栈s1,存储中间结果的栈s2;
- 从左至右扫描中缀表达式;
- 遇到操作数时,将其压入s2;
- 遇到运算符时,比较其与s1栈顶运算符的优先级:
- 如果s1为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈;
- 否则,若优先级比栈顶运算符的优先级高,则将运算符压入s1;
- 否则,将s1栈顶的运算符弹出并压入到s2中,再次转到步骤4-1与s1中新的栈顶运算符相比较;
- 遇到括号时:
- 如果是左括号“(”,则直接压入s1;
- 如果是右括号“)”,则依次弹出s1栈顶的运算符,并压入s2,直到遇到左括号为止,此时将这一对括号丢弃;
- 重复步骤2-5,直到表达式的最右边;
- 将s1中剩余的运算符依次弹出并压入s2;
- 依次弹出s2中的元素计算结果。
我们将使用C语言来实现栈的中缀表达式求值功能。具体步骤如下:
- 定义栈结构体和相关操作函数(如初始化、入栈、出栈、取栈顶元素等);
- 定义字符类型的栈用于存储运算符,定义浮点数类型的栈用于存储操作数和中间结果;
- 实现后缀表达式求值函数,使用上述算法;
- 编写主函数,测试中缀表达式求值函数。
具体代码
#include <stdio.h>
#include <stdlib.h>typedef struct Node {int data;struct Node *next;
} Node;typedef struct {Node *top;
} Stack;int is_operator(char ch) {return (ch == '+' || ch == '-' || ch == '*' || ch == '/');
}int priority(char op) {switch (op) {case '+':case '-':return 1;case '*':case '/':return 2;default:return 0;}
}int calculate(int a, char op, int b) {switch (op) {case '+':return a + b;case '-':return a - b;case '*':return a * b;case '/':return a / b;default:exit(1);}
}Stack *create_stack() { // 创建空栈Stack *stack = (Stack *)malloc(sizeof(Stack));stack->top = NULL;return stack;
}void push(Stack *stack, int data) { // 入栈操作Node *node = (Node *)malloc(sizeof(Node));node->data = data;node->next = stack->top;stack->top = node;
}int pop(Stack *stack) { // 出栈操作if (stack->top == NULL) {return -1; // 如果栈为空,则返回-1}Node *node = stack->top;int data = node->data;stack->top = node->next;free(node);return data;
}int top(Stack *stack) { // 返回栈顶元素if (stack->top == NULL) {return -1; // 如果栈为空,则返回-1}return stack->top->data;
}/*** 计算表达式结果的函数。** @param expression 表达式字符串* @return 表达式的计算结果*/
int evaluate_expression(char *expression) {Stack *s1 = create_stack(); // 操作数栈,用于存储操作数Stack *s2 = create_stack(); // 操作符栈,用于存储操作符for (int i = 0; expression[i] != '\0'; i++) {if (is_operator(expression[i])) { // 如果当前字符为操作符while (s2->top != NULL && priority(top(s2)) >= priority(expression[i])) {// 如果操作符栈不为空,并且栈顶操作符的优先级大于等于当前操作符的优先级int b = pop(s1); // 出栈一个操作数作为运算的右操作数int a = pop(s1); // 再出栈一个操作数作为运算的左操作数char op = pop(s2); // 出栈一个操作符int result = calculate(a, op, b); // 计算两个操作数和操作符的结果push(s1, result); // 将计算结果入栈到操作数栈中}push(s2, expression[i]); // 当前操作符入栈到操作符栈中} else if (expression[i] == '(') { // 如果当前字符为左括号push(s2, expression[i]); // 入栈到操作符栈中} else if (expression[i] == ')') { // 如果当前字符为右括号while (top(s2) != '(') { // 循环执行直到遇到左括号int b = pop(s1); // 出栈一个操作数作为运算的右操作数int a = pop(s1); // 再出栈一个操作数作为运算的左操作数char op = pop(s2); // 出栈一个操作符int result = calculate(a, op, b); // 计算两个操作数和操作符的结果push(s1, result); // 将计算结果入栈到操作数栈中}pop(s2); // 弹出左括号} else { // 如果当前字符为数字int num = expression[i] - '0'; // 将当前字符转换成数字while (expression[i + 1] >= '0' && expression[i + 1] <= '9') {// 如果下一个字符也是数字,则将其合并到一起num = num * 10 + expression[++i] - '0';}push(s1, num); // 将数字入栈到操作数栈中}}// 处理剩余的操作符while (s2->top != NULL) {int b = pop(s1); // 出栈一个操作数作为运算的右操作数int a = pop(s1); // 再出栈一个操作数作为运算的左操作数char op = pop(s2); // 出栈一个操作符int result = calculate(a, op, b); // 计算两个操作数和操作符的结果push(s1, result); // 将计算结果入栈到操作数栈中}return pop(s1); // 返回最终的计算结果
}int main() {char expression[100];printf("请输入中缀表达式:");scanf("%s", expression);int result = evaluate_expression(expression);printf("计算结果:%d\n", result);return 0;
}
相关文章:

数据结构 | 栈的中缀表达式求值
目录 什么是栈? 栈的基本操作 入栈操作 出栈操作 取栈顶元素 中缀表达式求值 实现思路 具体代码 什么是栈? 栈是一种线性数据结构,具有“先进后出”(Last In First Out, LIFO)的特点。它可以看作是一种受限的…...
vue2前端实现html导出pdf功能
1. 功能实现方案 1.html转换成canvas后生成图片导出pdf(本文选用) html转canvas插件:html2canvas是一款将HTML代码转换成Canvas的插件;canvas生成pdf:jsPDF是一个使用Javascript语言生成PDF的开源库 2.HTML代码转出…...

用 ChatGPT 辅助学好机器学习
文章目录一、前言二、主要内容🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 探索更高效的学习方法可能是有志者共同的追求,用好 ChatGPT,先行于未来。 作为一个人工智能大语言模型,ChatGPT 可以在帮助初…...
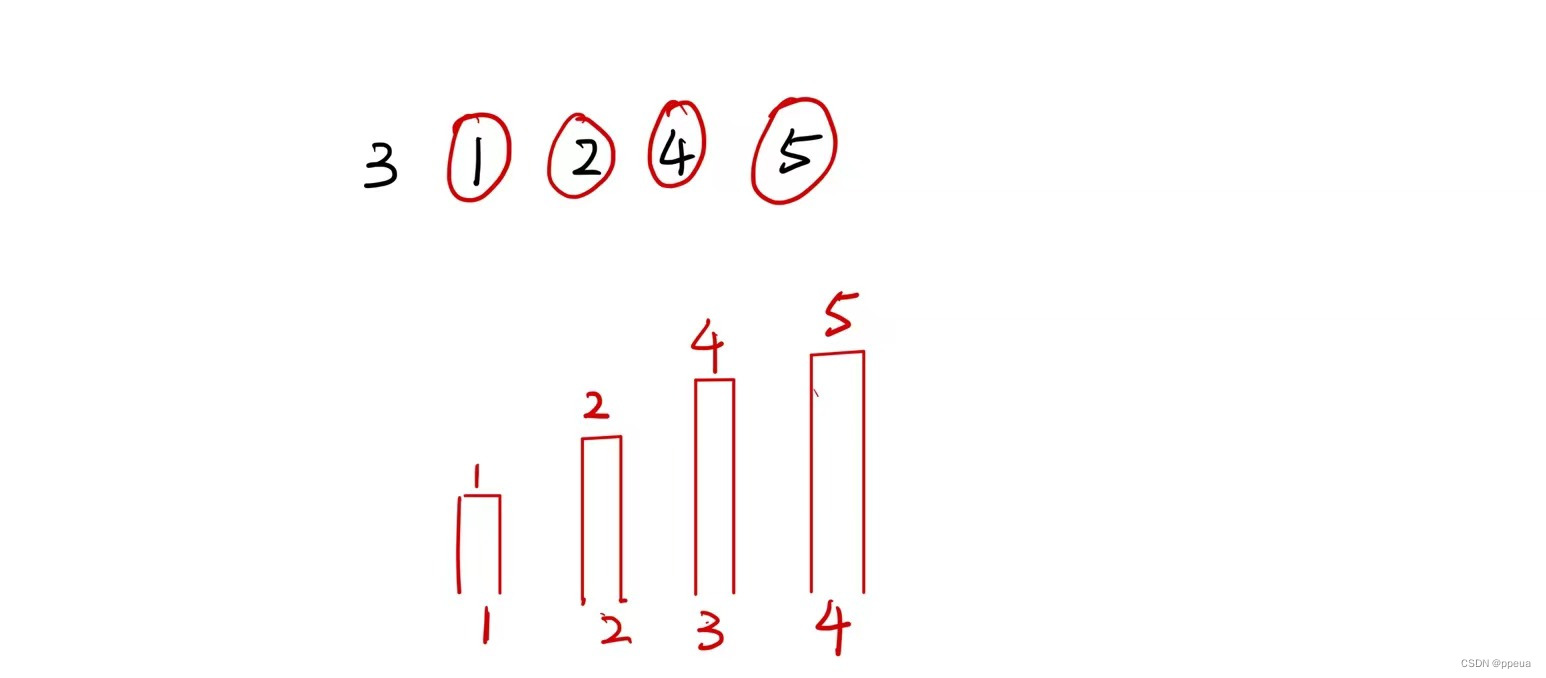
【动态规划】最长上升子序列(单调队列、贪心优化)
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...
海思SD3403/SS928V100开发(7)mcp2515-SPI转CAN驱动开发
1. 前言 需求: 需要一路can进行收发 分析: 根据目前使用较多的方案是使用主控端SPI接口 接入MCP2515芯片进行CAN协议转换 硬件: MCP2515->SPI2->SS928 2. Uboot开发 2.1 pinmux复用配置 2.1.1 修改uboot参数表 路径: osdrv/tools/pc/uboot_tools/ SS928V100…...
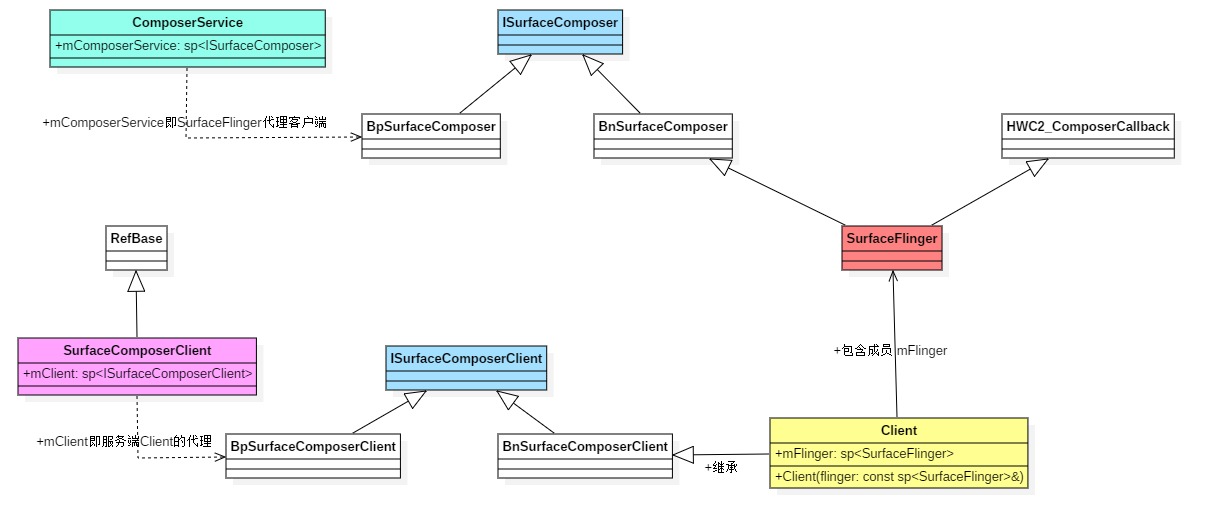
【安卓源码】SurfaceFlinger 启动及其与应用通信
1. surfaceFlinger 初始化和消息队列处理机制 surfaceflinger 的makefile 文件 /frameworks/native/services/surfaceflinger/Android.bp 235 cc_binary { 236 name: "surfaceflinger", 237 defaults: ["libsurfaceflinger_binary"], 238 i…...
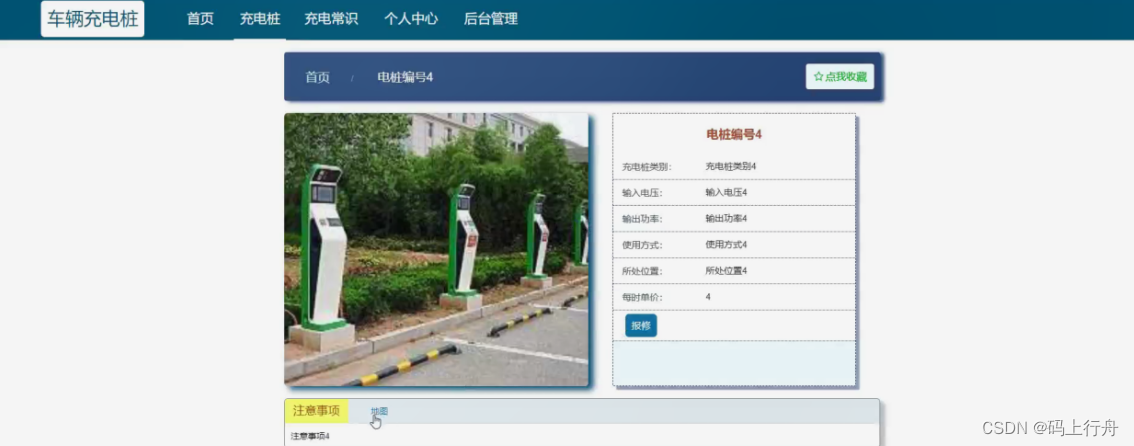
springboot车辆充电桩
sprinboot车辆充电桩演示录像2022开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7(一定要5.7版本) 数据库工具:Navicat11 开发软件:ecli…...

linux进程和进程通信编程(1)
What makes the desert beautiful is that somewhere it hides a well. 沙漠之所以美丽,是因为在它的某个角落隐藏着一口井. linux进程和进程通信编程(1)1.什么是进程2.进程id(pid)3.进程间通信的方法管道信号IPCSocket4.创建进程forkfork有三个返回值父…...

操作系统(1.3)--习题
一、课堂习题 1、一个作业第一 次执行时用了5min ,而第二次执行时用了6min,这说明了操作系统的( )特点。 A、并发性 B、共享性 C、虚拟性 D、不确定性 D 2、在计算机系统中,操作系统是( )。 A、处于裸机之上的第一层软件 B、处于硬件之下的低层软件 C、处于应用软件之上的系统软…...

刷题笔记之十三(有假币、最难的问题、因子个数)
目录 1. 求正数数组的最小不可组成和 2. 有假币 3. 继承时先调用父类的构造方法;类中的成员变量的初始化操作都在构造方法时进行 4. 学会并理解装箱拆箱,注意new出来的也可以拆!! 5. getDeclaredMethods()是标识类或接口的声明成员(这个表示public private 包访问权限 pro…...
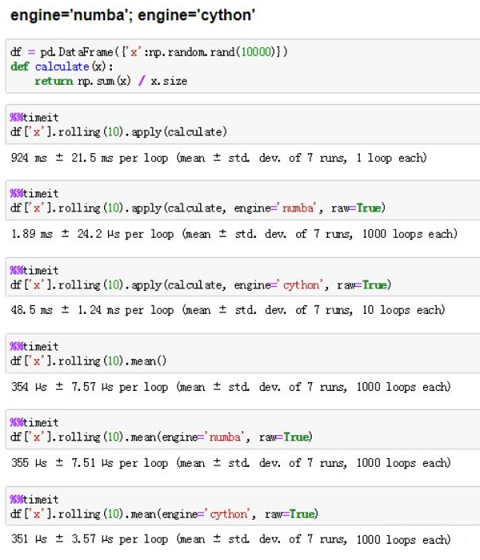
5个代码技巧,加速你的Python
5个代码技巧,加速你的Python 人生苦短,快学Python! Python作为一种功能强大的编程语言,因其简单易学而受到很多初学者的青睐。它的应用领域又非常广泛:科学计算、游戏开发、爬虫、人工智能、自动化办公、Web应用开发…...

字节跳动软件测试岗,前两面过了,第三面HR天坑!竟然跟我说……
阎王易见,小鬼难缠。我一直相信这个世界上好人居多,但是也没想到自己也会在阴沟里翻船。我感觉自己被字节跳动的HR坑了。在这里,我只想告诫大家,offer一定要拿到自己的手里才是真的,口头offer都是不牢靠的,…...
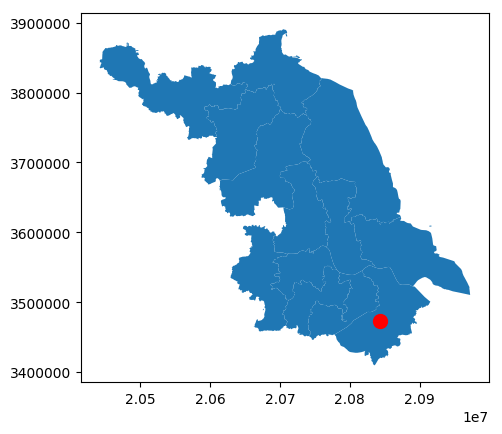
[数据分析与可视化] Python绘制数据地图1-GeoPandas入门指北
本文主要介绍GeoPandas的基本使用方法,以绘制简单的地图。GeoPandas是一个Python开源项目,旨在提供丰富而简单的地理空间数据处理接口。GeoPandas扩展了Pandas的数据类型,并使用matplotlib进行绘图。GeoPandas官方仓库地址为:GeoP…...

ChatGPT加强版GPT-4面世,打工人的方式将被颠覆
🔗 运行环境:chatGPT,GPT-4 🚩 撰写作者:左手の明天 🥇 精选专栏:《python》 🔥 推荐专栏:《算法研究》 #### 防伪水印——左手の明天 #### 💗 大家好&#…...
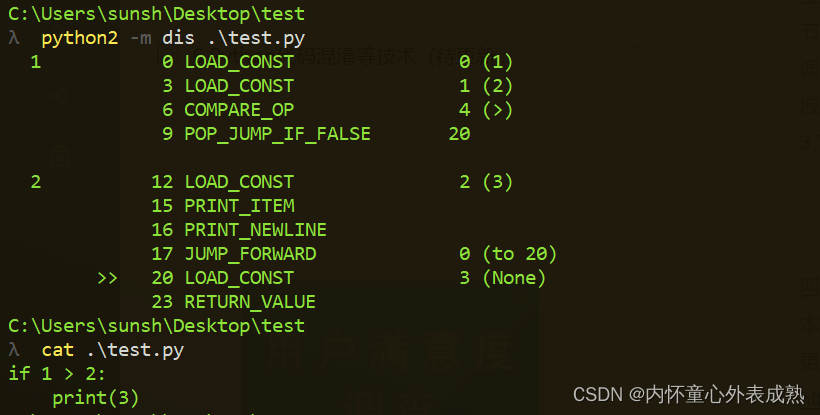
Python逆向及相关知识
今天第二次看见python字节码的逆向题,然后发现了一个介绍Python逆向的文章,所以把文章里的内容简单整理记录一下。 文章参考:https://www.cnblogs.com/blili/p/11799398.html Python运行原理: 一.什么是Python Python 是一种解…...
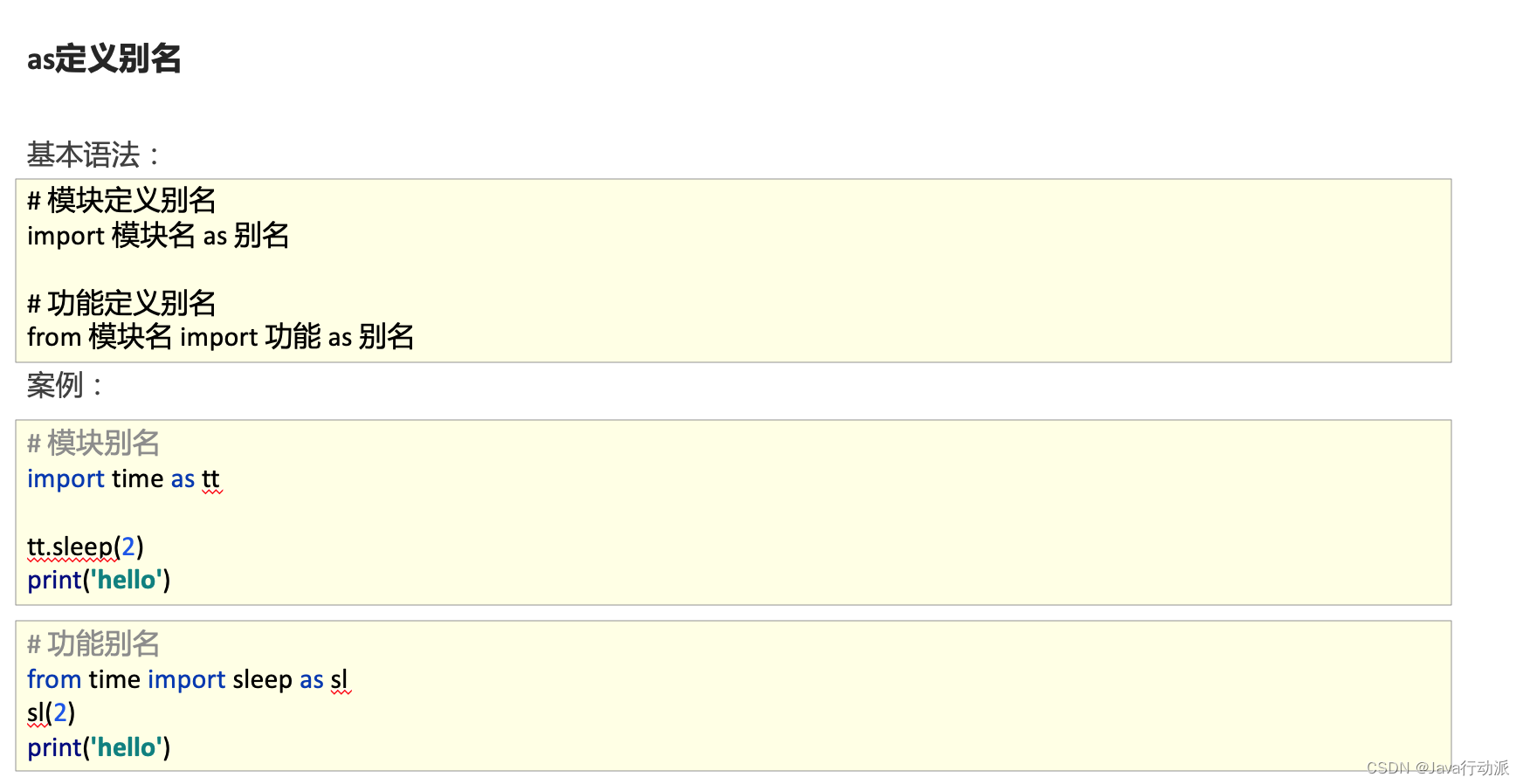
Python基础语法、注意点加实例全解
本篇文章我们讲解Python最基础语法,包含:数据类型、注释、变量、类型转换、命名规范、运算符、字符串拼接、字符串格式化、if条件判断、while循环、for循环、函数、读取文件、写入文件、异常捕获、包导入等。通过讲解语法注意事项实例代码详解࿰…...

ETH RPC搭建
配置选择先是看了aws、谷歌云、阿里云这个配置都要1-2wrmb一个月,太贵了问了很多朋友,打算用hetzner,50欧一个月足以我选的配置:64gb,2tb ssd开好后在邮箱收到信息链接后按以下步骤安装系统:https://0o0.me…...

南京邮电大学数据库第一次课后作业
1.单选题 (5分) (B)是存储在计算机内有结构的数据的集合。 (A)数据库系统 (B)数据库 (C)数据库管理系统 (D)数据结构 2.单选题 (5分) 数据库的特点之一是数据的共享,严格的讲,这里的…...

近期投简历、找日常实习的一些碎碎念(大二---测试岗)
嘿嘿嘿,我又回来了,相信不少兄弟已经发现我似乎已经断更了好久,哈哈,我是尝试去找实习,投简历面试去了。 先说一下背景。 目录 背景 求职进行中 简历 投递和沟通 收获和感受 背景 博主,大二软件工程…...
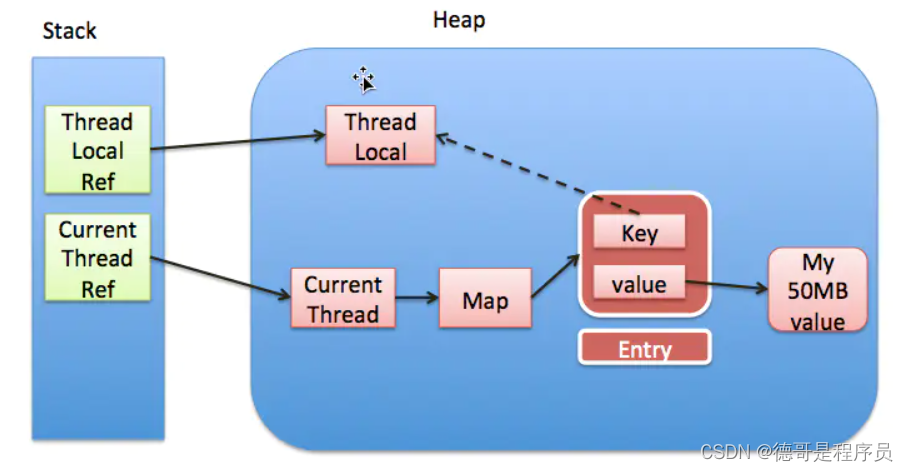
ThreadLocal的使用
1. ThreadLocal介绍 ThreadLocal顾名思义,就是线程的本地变量,只有当前线程可见,对其他线程来说是封闭且隔离的。每一个线程为自己本身创建ThreadLocal变量,只有当前线程可以访问,其他的线程不可以,从根源…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
