代码随想录算法训练营第22天-leetcode-回溯算法part01:
#回溯算法理论基础
能解决的问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
第77题. 组合
力扣题目链接(opens new window)
给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。
示例: 输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4],
注意:
1、对于是递归回溯问题,用树图来考虑问题!+使用基本结构
同时,也要积极分析如何剪枝
2、路径类问题的标准套路:
在函数外开辟path 和 ans 一层空间 ans=(int**)malloc:一层空间,二层空间还没开辟
终止条件 if(一条路径完成了) 把path放入ans数组
先开辟ans的二层空间,ans【i】=(int*)malloc
放入path的过程需要用循环一个个放入,直接=path的话,后面会随path修改而修改
递归体:填充path
3、报错分析:
遇见heap堆错误,找malloc相关的;遇见stack栈报错,找函数内数组是否越界
4、returnsize 和 return column
*returnsize 在函数调用中无需&,且指向个数,而非下标
column的赋值过程:*column是正常数组,先为*column开辟空间,*column【第几个,<returnsize】=ans【第几个】有多少个二层元素
分析:


代码:
void bf(int *path,int n,int start,int k,int *pathlength,int **ans,int *returnSize){if(*pathlength == k-1){//路径类问题的标准输出ans[++(*returnSize)]=(int *)malloc(sizeof(int)*k);for (int i=0;i<k;i++){ans[*returnSize][i]=path[i];}return;}for(int i=start;i<=n-(k-*pathlength-2);i++){//遍历各个树//剪枝:如果后面全放进去,也达不到k个个数,那么就不考虑了path[++(*pathlength)]=i;bf(path,n,i+1,k,pathlength,ans,returnSize);(*pathlength)--;//回溯 步骤!!}
}int** combine(int n, int k, int* returnSize, int** returnColumnSizes) {int **ans=(int **)malloc(sizeof(int *)*200001);*returnSize=-1;int pathlength=-1;//考虑路径,用到path,pathlengthint *path=(int *)malloc(sizeof(int )*k);bf(path,n,1, k, &pathlength,ans,returnSize);//returnsize不需要&(*returnSize)++;//returnsize指向数组的实际大小*returnColumnSizes=(int*)malloc(sizeof(int )*(*returnSize));//column的意义for(int i=0;i<(*returnSize);i++){(*returnColumnSizes)[i]=k;}return ans;
}216.组合总和III
力扣题目链接(opens new window)
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
- 所有数字都是正整数。
- 解集不能包含重复的组合。
示例 1: 输入: k = 3, n = 7 输出: [[1,2,4]]
示例 2: 输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]
void bp(int **ans,int *size,int *path,int *p,int k,int n,int start,int sum){if(sum>n) return;//剪枝if(sum==n && *p==k){ans[*size]=(int *)malloc(sizeof(int)*k);for (int i=0;i<k;i++){ans[*size][i]=path[i];}(*size)++;return;//不要忘记写return}else if(*p==k){//另外一种终止情况return;}for(int i=start;i<=9;i++){path[(*p)++]=i;bp(ans, size, path, p, k, n, i+1, sum+i);//i+1,而不是start+1(*p)--;}
}int** combinationSum3(int k, int n, int* returnSize, int** returnColumnSizes) {int **ans=(int **)malloc(sizeof(int *)*500);int size=0;int *path=(int *)malloc(sizeof(int)*k);int p=0;bp(ans, &size,path, &p, k, n, 1, 0);*returnSize=size;*returnColumnSizes=(int *)malloc(sizeof(int)*(size));for (int i=0;i<size;i++){(*returnColumnSizes)[i]=k;//要加括号}return ans;}17.电话号码的字母组合
力扣题目链接(opens new window)
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
char phoneMap[11][5] = {"\0", "\0", "abc\0", "def\0", "ghi\0", "jkl\0", "mno\0", "pqrs\0", "tuv\0", "wxyz\0"};void bp(char**ans,int *size,char *path,int *p,int len,char* digits,int d){if(*p==len){ans[*size] =(char*)malloc(sizeof(char)*(len+1));for(int i=0;i<len;i++){ans[*size][i]=path[i];printf("%c",path[i]);} ans[*size][len]='\0';printf("\n");(*size)++;return;}int number= digits[d]-'0';char * nowd=phoneMap[number];int dlen=strlen(nowd);for(int i=0;i<dlen;i++){char new=nowd[i];path[(*p)++]=new;bp(ans, size, path,p, len, digits,d+1);(*p)--;}}char** letterCombinations(char* digits, int* returnSize) {int len=strlen(digits);char**ans=(char**)malloc(sizeof(char*)*pow(4,len));int size=0;if (len==0) {*returnSize=0;return ans;}char *path=(char*)malloc(sizeof(char)*(len+1));int p=0;bp(ans,&size, path, &p, len, digits, 0);*returnSize=size;return ans;}相关文章:

代码随想录算法训练营第22天-leetcode-回溯算法part01:
#回溯算法理论基础 能解决的问题: 组合问题:N个数里面按一定规则找出k个数的集合切割问题:一个字符串按一定规则有几种切割方式子集问题:一个N个数的集合里有多少符合条件的子集排列问题:N个数按一定规则全排列&…...

MySql 触发器、存储器练习
一: 触发器 1、建立两个表:goods(商品表)、orders(订单表) 查看数据库:mysql> show databases; 使用数据库:mysql> use mydb16_trigger; 创建goods表: mysql> create table goods(gid char(8) not null primary key, …...

【Plotly-驯化】一文教您画出Plotly中动态可视化饼图:pie技巧
【Plotly-驯化】一文教您画出Plotly中动态可视化饼图:pie技巧 本次修炼方法请往下查看 🌈 欢迎莅临我的个人主页 👈这里是我工作、学习、实践 IT领域、真诚分享 踩坑集合,智慧小天地! 🎇 免费获取相关内…...

Mirror学习笔记(一) 简介
文章目录 一、常规学习:Mirror核心功能有服务器和主机 二、时间戳批处理时间戳 三、TCP和UDP四、CCU(同时在线人数)五、SyncDirection(同步方向)六、RTT(往返时间)七、Connection Quality(连接质量)八、Lag Compensati…...
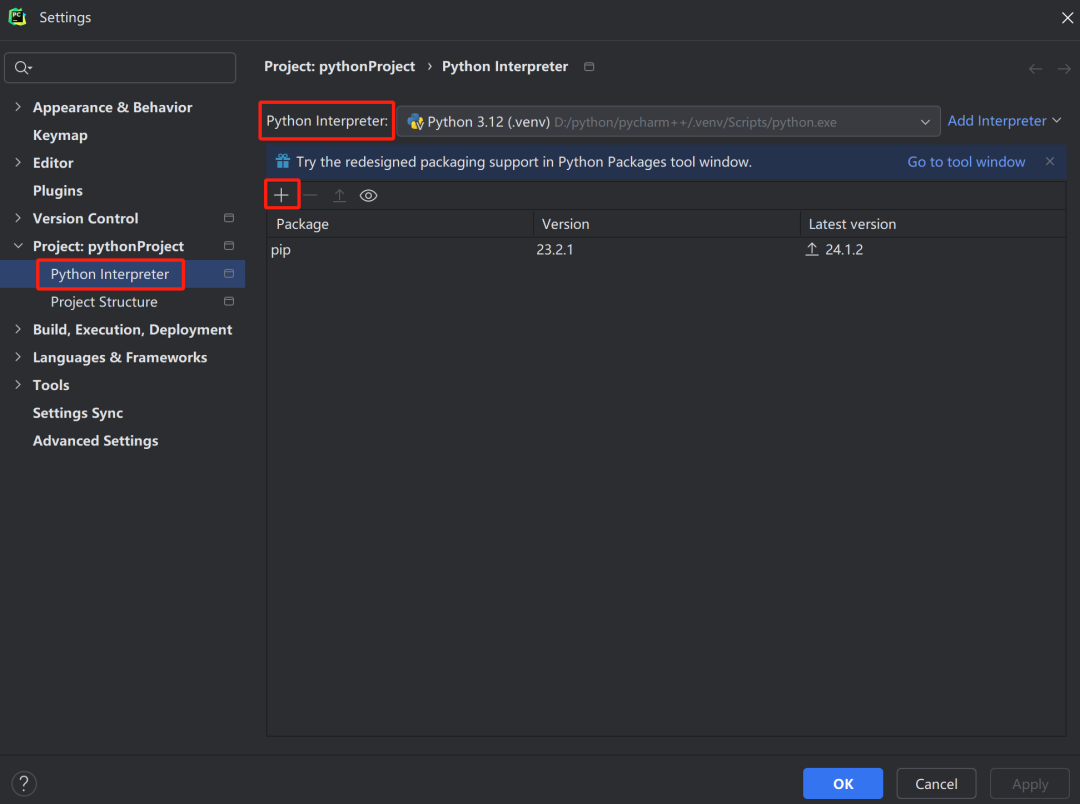
终端pip安装包后,Pycharm却导入失败?新手别慌,3招搞定!
很多小伙伴在学习Python的过程中,都会遇到这种情况:明明在终端用pip安装好了需要的包,但在Pycharm中导入时却报错。难道是安装姿势不对? 例如在cmd中已经有了pandas,但是去pycharm中导入pandas显示没有 先别急着怀疑人生,这很可能是因为pip安装包的路径和Pycharm项目使用…...

Redis 与 Scrapy:无缝集成的分布式爬虫技术
1. 分布式爬虫的概念 分布式爬虫系统通过将任务分配给多个爬虫节点,利用集群的计算能力来提高数据抓取的效率。这种方式不仅可以提高爬取速度,还可以在单个节点发生故障时,通过其他节点继续完成任务,从而提高系统的稳定性和可靠性…...

大厂linux面试题攻略四之Linux网络服务(一)
一、Linux网络服务-SSH服务 1.哪些设置能够提升SSH远程管理的安全等级? ssh的登录验证方式 ssh的登录端口和监听设置: 配置文件: /etc/ssh/sshd_config #Port 22 #ssh服务默认监听端口 #ListenAddress 0.0.0.0 #ssh服务…...

【Pulling fs layer】Linux使用docker-compose的时候,一直Pulling fs layer
当Docker在拉取镜像时卡在“pulling fs layer”阶段,可以通过重启Docker服务来解决。 具体步骤如下: 首先,尝试重启Docker服务。可以通过运行以下命令来重启Docker服务: systemctl restart docker 这个命令会重启Docker服务…...

最新保姆级教程使用WildCard开通Claude3升级ChatGPT4.0(2024.8)
如何使用 WildCard 服务注册 Claude3 随着 Claude3 的震撼发布,最强 AI 模型的桂冠已不再由 GPT-4 独揽。Claude3 推出了三个备受瞩目的模型:Claude 3 Haiku、Claude 3 Sonnet 以及 Claude 3 Opus,每个模型都展现了卓越的性能与特色。其中&a…...

layui 乱入前端
功能包含 本实例代码为部分傻瓜框架,插入引用layui。因为样式必须保证跟系统一致,所以大部分功能都是自定义的。代码仅供需要用layui框架,但原项目又不是layui搭建的提供解题思路。代码较为通用 自定义分页功能自定义筛选列功能行内编辑下拉、…...
中国十大顶级哲学家,全球公认的伟大思想家颜廷利:人类为何拥有臀部
人类为何拥有臀部?若众生皆无此部位,又如何能寻得一处真正属于自己的“座位”?在博大精深的中国传统文化中,汉字“座”与“坐”均蕴含“土”字元素。在易经的智慧里,作为五行之一的“土”,象征着人类社会的…...

Threejs中导入GLTF模型克隆后合并
很多场景中会需要同一个模型很多次,但是如果多次加载同一个模型会占用很高的带宽,导致加载很慢,因此就需要使用clone,也就是加载一个模型后,其他需要使用的地方使用clone的方式复制出多个同样的模型,再改变…...

今日arXiv最热大模型论文:北京大学最新综述:视觉大模型中的漏洞与攻防对抗
近年来,视觉语言大模型(LVLM)在文本转图像、视觉问答等任务中大放异彩,背后离不开海量数据、强大算力和复杂参数的支撑。 但是!大模型看似庞大的身躯背后却有一颗脆弱的“心脏”,极易受到攻击。攻击者可以…...
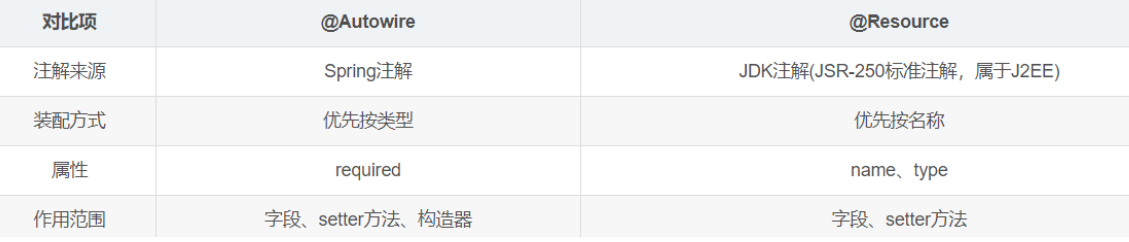
为什么IDEA中使用@Autowired会被警告
我们在使用IDEA编码时,如果用到了Autowired注解注入bean,会发现IDEA会给代码标个波连线,鼠标移动上去,会发下idea提示:不推荐使用Filed injection,这是Spring的核心DI(Dendency Injection&#…...

uniapp使用cover-view,使用@click无效
最近要做直播详情页面,用的是第三方直播链接,需要在该页面上放两个按钮,点击按钮需要弹出相关商品及优惠券。类似于抖音直播页面。 第三方链接使用的是web-view进行展示。由于该组件优先级太高,正常的前端组件无法在该页面浮现展…...

Postman 接口测试工具简易使用指南
一、Postman是什么? 我通过kimi问了这样一个问题,它给我的回答是这样的: 它的回答也算比较中规中矩,简单的说postman实际上就是一款接口测试工具,同时它还可以编写对应的测试脚本以及自动生成对应的API文档,结合我的习惯来说&am…...

Move生态:从Aptos和Sui到Starcoin的崛起
区块链技术自诞生以来,已经经历了多个发展阶段和技术迭代。近年来,随着智能合约平台的不断演进,以Move语言为核心的生态系统逐渐崭露头角。Move语言以其安全性、灵活性和高效性吸引了大量开发者和项目方的关注。在Move生态中,Apto…...

MacOS DockerDesktop配置文件daemon.json的位置
如果因为通过可视化页面修改配置错误导致客户端启动不起来,可以去找对应的配置文件通过 vim 修改后重启客户端 cd ~/.docker/...

从光速常数的可变性看宇宙大爆炸的本质
基于先前关于光速本质的讨论,让我们从函数图像看看宇宙大爆炸到底是什么。 先前已经讨论过,在量子尺度上,长度的实际对应物是频率的差异,因为只有频率差异才能在这个尺度上区分相邻时空的两点,而两点之间“差异的大小”…...

敢不敢跟我一起搭建一个Agent!不写一行代码,10分钟搞出你的智能体!纯配置也能真正掌握AI最有潜力的技术?AI圈内人必备技能
说一千道一万,不如实地转一转。学了那么久的AI Agent的概念了,是时候该落地一个Agent看看自己的掌握程度了对不对,我们都理解大脑是自动节能的,但是知识的确需要倒逼自己一把才能真的掌握,不瞒大家说,笔者对…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

Windows 下端口占用排查与释放全攻略
Windows 下端口占用排查与释放全攻略 在开发和运维过程中,经常会遇到端口被占用的问题(如 8080、3306 等常用端口)。本文将详细介绍如何通过命令行和图形化界面快速定位并释放被占用的端口,帮助你高效解决此类问题。 一、准…...

