牛客寒假集训营6 E 阿宁的生成树
E-阿宁的生成树_2023牛客寒假算法基础集训营6 (nowcoder.com)
开始慢慢补牛牛的题
题意:
最小生成树+质数距离
思路:
最小生成树一共就两种算法,我们考虑Prim的过程
初始连通块是1,然后考虑拿1和其他的结点连边
当j-i<=k时边权是gcd,j-i>k时边权是lcm
考虑j-1>k的点
即j>k+1
即j>=k+2
显然,对于[k+2,n]的结点来说,边权都是gcd(1,i),都为1
对于[2,k+2)的点,如果是和结点1连边,边权就是i,因此对于这些点的边权最多就是i
但是如果区间[2,k+2]的点和附近区间k的点连gcd的边,边权可能会变小
这里考虑暴力,用已经松弛的[k+2,n]的结点去松弛区间[2,k+2)的点
如果遍历到的已经松弛的结点是质数,那么边权一定为1,所以可以break
小trick:1e8以内的质数距离最多200,因此时间复杂度是O(n*200),不会超时
#include <bits/stdc++.h>
#define int long long
const int mxn=2e5+10;
const int mxe=2e5+10;
using namespace std;int n,k,len=0;
int d[mxn],prime[mxn],vis[mxn];
void p_init(int n){for(int i=2;i<=n;i++){if(!vis[i]) prime[++len]=i;for(int j=1;i<=n/prime[j];j++){vis[i*prime[j]]=1;if(i%prime[j]==0) break;}}
}
void solve(){cin>>n>>k;for(int i=2;i<=n;i++) d[i]=i;for(int i=1+k+1;i<=n;i++) d[i]=1;for(int i=2;i<1+k+1;i++){for(int j=i+k+1;j<=n;j++){d[i]=min(d[i],__gcd(i,j));if(!vis[j]) break;}}int ans=0;for(int i=2;i<=n;i++) ans+=d[i];cout<<ans<<'\n';
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;p_init(2e5);while(__--)solve();return 0;
}相关文章:

牛客寒假集训营6 E 阿宁的生成树
E-阿宁的生成树_2023牛客寒假算法基础集训营6 (nowcoder.com)开始慢慢补牛牛的题题意:最小生成树质数距离思路:最小生成树一共就两种算法,我们考虑Prim的过程初始连通块是1,然后考虑拿1和其他的结点连边当j-i<k时边权是gcd&…...
)
嵌入式C基础知识(10)
C语言如何实现一个频繁使用短小函数,C如何实现?C语言可以使用宏定义实现一个短小函数,如下面例子所示。但是宏定义语句不会进行检查,并且对书写格式有过分的讲究。比如MAX和括号之间不能有空格,每个参数都要放在括号里…...

TC3xx FlexRay™ 协议控制器 (E-Ray)-01
1 FlexRay™ 协议控制器 (E-Ray) E-Ray IP 模块根据为汽车应用开发的 FlexRay™ 协议规范 v2.1 执行通信【performs communication according to the FlexRay™ 1) protocol specification v2.1】。使用最大指定时钟,比特率可以编程为高达 10 Mbit/s 的值。连接到物…...

优劣解距离法TOPSIS——清风老师
TOPSIS法是一种常用的综合评价方法,能充分利用原始数据的信息,其结果能精确地反映各评价方案之间的差距。 基本过程为先将原始数据矩阵统一指标类型(一般正向化处理)得到正向化的矩阵,再对正向化的矩阵进行标准化处理…...
【Unity3D】Shader常量、变量、结构体、函数
1 源码路径 Unity Shader 常量、变量、结构体、函数一般可以在 Unity Editor 安装目录下面的【Editor\Data\CGIncludes\UnityShader】目录下查看源码,主要源码文件如下: UnityCG.cgincUnityShaderUtilities.cgincUnityShaderVariables.cginc 2 Shader 常…...

LeetCode 刷题系列 -- 496. 下一个更大元素 I
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。对于每个 0 < i < nums1.length ,找出满…...
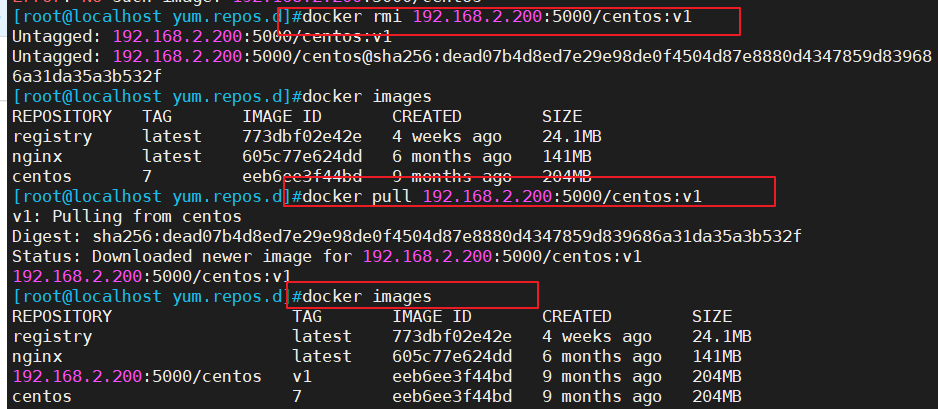
Docker 搭建本地私有仓库
一、搭建本地私有仓库有时候使用Docker Hub这样的公共仓库可能不方便,这种情况下用户可以使用registry创建一个本地仓库供私人使用,这点跟Maven的管理类似。使用私有仓库有许多优点:1)节省网络带宽,针对于每个镜像不用…...

XML中的CDATA且mybatis中特殊字符转义
如果想看如果CDATA在mybatis的xml文件中使用的可以直接跳转。 CDATA1 XML中的CDATA1.1 为什么叫CDATA1.2 CDATA在XML中的语法1.3 CDATA在XML中的例子1.4 CDATA规则2 Mybatis中的CDATA2.1 Mybatis中使用XML转义序列转义2.2 Mybatis中使用CDATA转义2.3 mybatis中使用CDATA需注意的…...

位运算 | 1356. 根据数字二进制下 1 的数目排序
LeetCode 1356. 根据数字二进制下 1 的数目排序 给你一个整数数组 arr 。请你将数组中的元素按照其二进制表示中数字 1 的数目升序排序。如果存在多个数字二进制中 1 的数目相同,则必须将它们按照数值大小升序排列。 文章讲解https://www.programmercarl.com/1356.%…...

React Hooks之useState详解
1. 什么是Hooks? React官方简介:Hook 是 React 16.8 的新增特性。它可以让你在不编写 class 的情况下使用 state 以及其他的 React 特性。 本文中讲解的useState就是React中的其中一个Hook。 2. useState useState 通过在函数组件里调用它来满足给组件添…...

选购交换机的参数依据和主要的参数指标详解
如何选购交换机?用什么交换机?在选购交换机时交换机的优劣无疑十分的重要,而交换机的优劣要从总体构架、性能和功能三方面入手。交换机选购时。性能方面除了要满足RFC2544建议的基本标准,即吞吐量、时延、丢包率外,随着…...
)
Connext DDS属性配置参考大全(1)
介绍属性QoS策略存储名称/值(字符串)对,可用于配置Connext DDS的某些参数,这些参数未通过正式的QoS策略公开。 属性QoS策略存储实体的名称/值对。名称和值都是字符串。在核心库用户手册的“Property QosPolicy(DDS Extension)”部分中找到有关RTI Connext DDS属性QoS的更…...
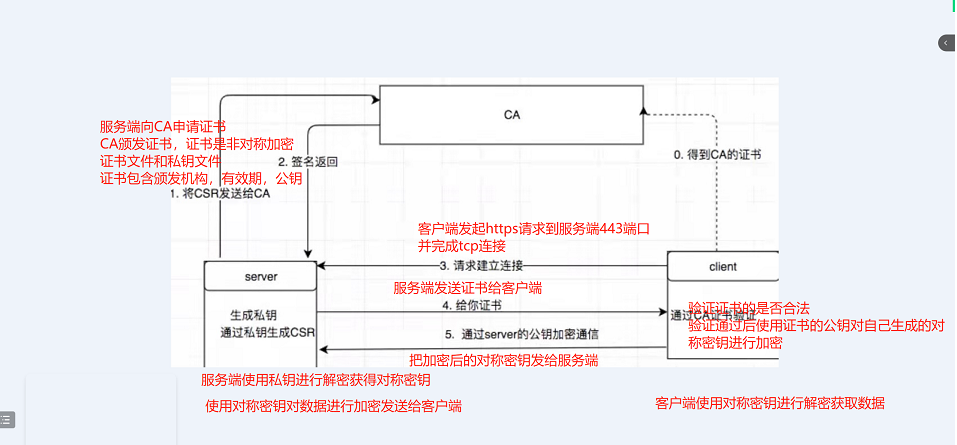
Docker安全
容器的安全性问题的根源在于容器和宿主机共享内核。如果容器里的应用导致Linux内核崩溃,那么整个系统可能都会崩溃。 与虚拟机是不同的,虚拟机并没有与主机共享内核,虚拟机崩溃一般不会导致宿主机崩溃 一、Docker 容器与虚拟机的区别 1、隔…...

刷题记录:牛客NC20279[SCOI2010]序列操作
传送门:牛客 题目描述: lxhgww最近收到了一个01序列,序列里面包含了n个数,这些数要么是0,要么是1,现在对于这个序列有五种变换操作和询问操作: 0 a b 把[a, b]区间内的所有数全变成0 1 a b 把[a, b]区间内的所有数全…...

Fluent Python 笔记 第 6 章 使用一等函数实现设计模式
虽然设计模式与语言无关,但这并不意味着每一个模式都能在每一门语言中使用。1996 年,Peter Norvig 在题为“Design Patterns in Dynamic Languages”(http://norvig.com/design- patterns/)的演讲中指出,Gamma 等人合著的《设计模式:可复用面…...

windbg-应用层实时调试
调试符号windbg使用一个或多个目录来存放符号条件,并使用环境变量_NT_SYMBOL_PATH来指向这些环境变量的位置,对操作系统内部模块的符号文件,一般用http://msdl.microsoft.com/download/symbols配置如下:SRV*C:\Symbols*http://msd…...

【Python语言基础】——Python NumPy 数组索引
Python语言基础——Python NumPy 数组索引 文章目录 Python语言基础——Python NumPy 数组索引一、Python NumPy 数组索引一、Python NumPy 数组索引 访问数组元素 数组索引等同于访问数组元素。 您可以通过引用其索引号来访问数组元素。 NumPy 数组中的索引以 0 开头,这意味…...
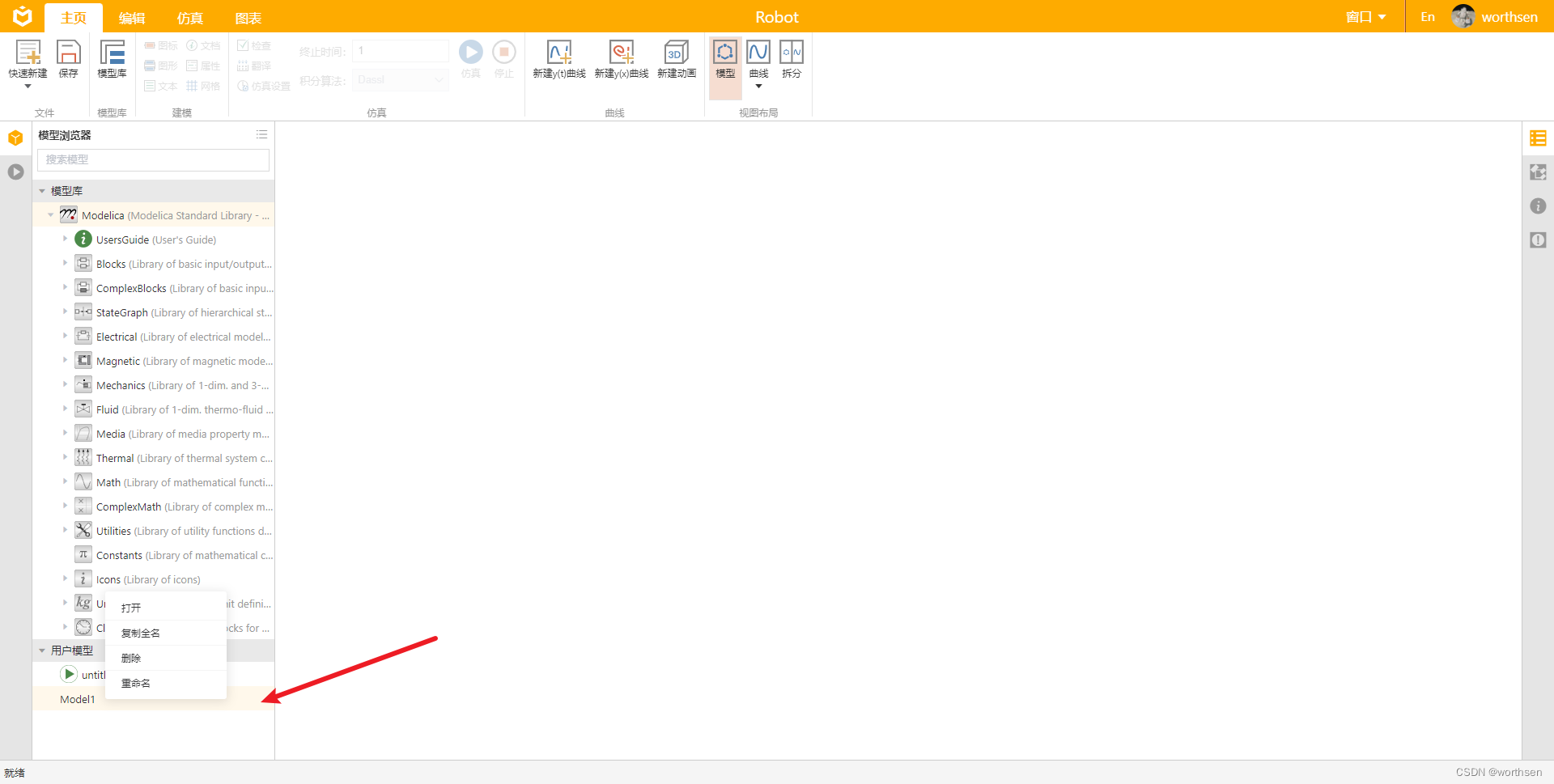
MWORKS--MoHub介绍
MWORKS--MoHub介绍1 介绍1.1 简介1.2 功能特征2 快速上手2.1 进入工作台2.2 新建仓库并进入建模空间2.3 建模进入建模工作空间加载模型库新建模型2.4 仿真2.5 后处理曲线、动画2.6 查看模型信息3 使用手册参考1 介绍 1.1 简介 MWORKS.MoHub 支持工业知识、经验、数据的模型化…...
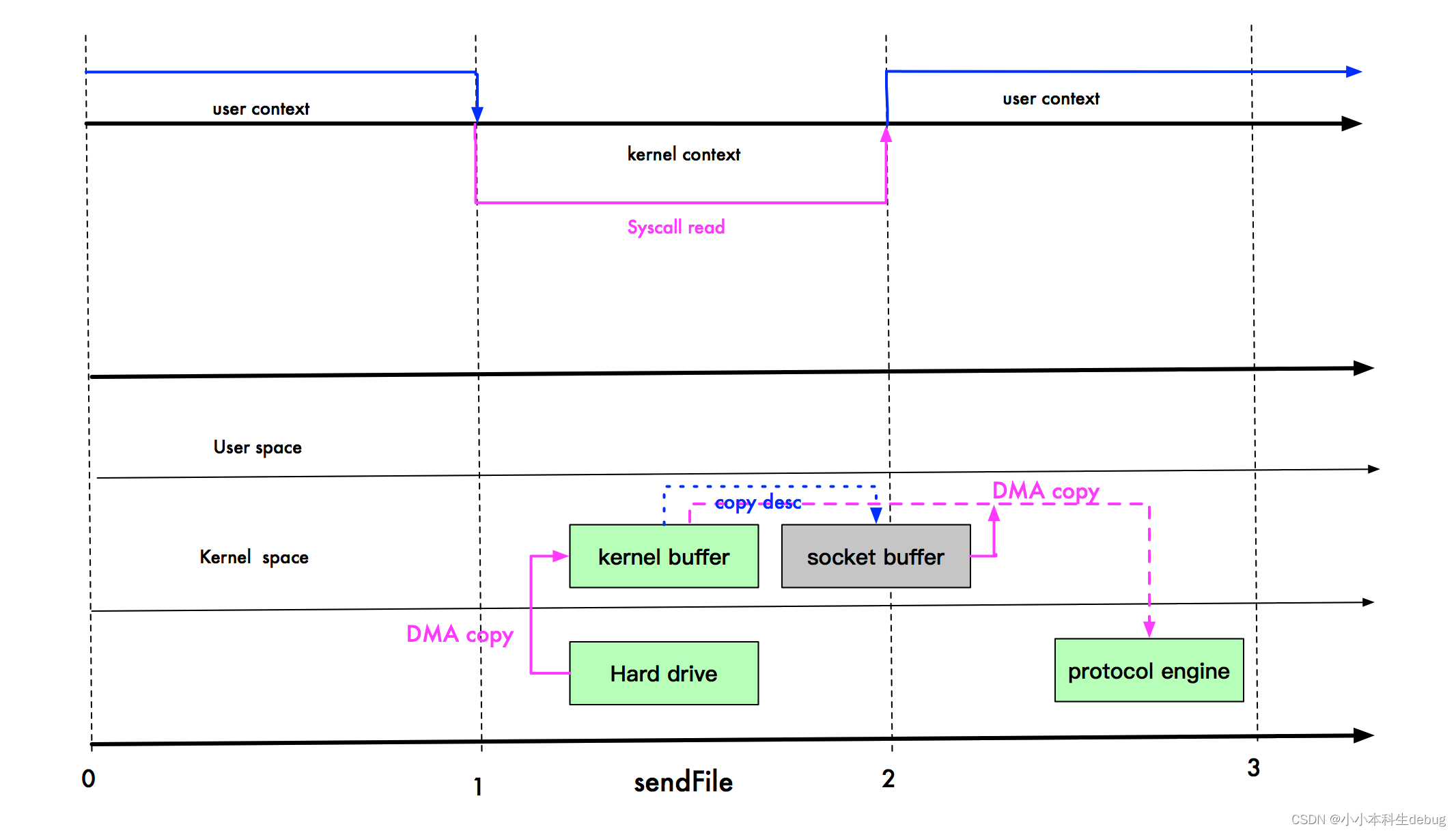
Netty零拷贝机制
Netty零拷贝机制一:用户空间与内核空间二:传统IO流程三:零拷贝常见的实现方式1. mmap write2. sendfile四:Java中零拷贝五:Netty 中如何实现零拷贝1. CompositeByteBuf 实现零拷贝2. wrap 实现零拷贝3. slice 实现零拷…...
C++:提高篇: 栈-寄存器和函数状态:windows X86-64寄存器介绍
寄存器1、什么是寄存器2、寄存器分类3、windows X86寄存器命名规则4、寄存器相关术语5、寄存器分类5.1、RAX(accumulator register)5.2、RBX(Base register)5.3、RDX(Data register)5.4、RCX(counter register)5.5、RSI(Source index)5.6、RDI(Destination index)5.7、RSP(stac…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...
