2024年7月个人工作生活总结
本文为 2024年7月工作生活总结。
研发编码
“康威定律(Conway’s Law)”思考
康威定律是 50 年前(1967 年)由 梅尔文·康威 提出的,最初的说法如下:
Any organization that designs a system (defined broadly) will produce a design whose structure is a copy of the organization’s communication structure.
— Melvin E. Conway
直译:一个组织的系统通常被设计成这个组织通信结构的副本。
可理解为:任何设计系统的组织,必然会产生以下设计结果:即其结构就是该组织沟通结构的写照。简单来说: 产品必然是其组织沟通结构的缩影。
什么样的组织架构,什么样的团队,就产生什么样的架构。这边的系统,用java的居多,上面还成立了java技术和架构评审专家组,专门对java相关技术进行全面指导。而我偏向于设备端,因此维护原有软件是用C++,而新的工程,按我目前的技术栈,最快的是用golang开发。但由于组织架构一些原因,我也会做些网页相关的开发。关于架构的话题都比较宏大,这里不展开。
一个项目
某项目,从去年年中就开始做需求分析、写方案,接着专家评审,接着开发,然后没下文了。主要是业主方一直在走流程,年初问了情况后,以为不再做了,但这个月又开始找专家评审了。于是完善方案,然后评审。由于规格比较高,写PPT时明显觉得紧张,直到PPT结束了,进行专家质询阶段,才从容应对。其实懂是懂的,只是见的场面少。
一个线上问题的记录
搞了个线上的问题出来,上线三天才暴露出问题。警告信息没有被关注到,也没有专门的人员做测试。但归根到底还是在我这边,该问题是在某些特定场景下出现的。每次发布,我只是简单测试记录的几个用例,通过后,放生产环境,再做验证。发现当天晚上去公司解决了。次日领导找,同时惊动大领导,被大批一顿,汗流浃背。后面构思了自测方案,但没有放到当月工作重点,开会时又被批。回顾总结,主要是做的事务太分散了,同时做的几个事没有必然的关联,不管是从事务管理角度,还是从技术栈角度。当然还是自己的问题。
有同是交了转正表的同事问转正的事,我回复说,看来今年是没戏了。
生活记录
开始跑步
月初决定开始做些锻炼的事情。第一次跑时,距离约1公里,但疼了2天。隔天跑,一周多后才有好转。如今天亮得早,如不熬夜,早上6点半可起,跑十来分钟,加上其它的锻炼,差不多了。不追求指标,不追求天天跑,只求身体不太虚即可。
月底总结,真正能跑的时间不到半个月,不过也算不错了。
借书买书
无意间看了《幼学琼林》,发现这书不错,篇幅长,内容多,个别卷可以诵读。在旧书摊找了几次,没找到这本书,《左传》、《战国策》也是一直没找到。在网上买了本几块钱的注音版,再在图书馆借注释版,配合起来,顺便修正注音。
相关文章:

2024年7月个人工作生活总结
本文为 2024年7月工作生活总结。 研发编码 “康威定律(Conway’s Law)”思考 康威定律是 50 年前(1967 年)由 梅尔文康威 提出的,最初的说法如下: Any organization that designs a system (defined broa…...

快速方便地下载huggingface的模型库和数据集
快速方便地下载huggingface的模型库和数据集 方法一:用于使用 aria2/wgetgit 下载 Huggingface 模型和数据集的 CLI 工具特点Usage 方法二:模型下载【个人使用记录】保持目录结构数据集下载不足之处 方法一:用于使用 aria2/wgetgit 下载 Hugg…...

JAVA小白学习日记Day10
1.线程锁 使用Runnable接口和Lambda表达式: 在 EasyThreadA 类的 mainA 方法中,通过创建 Runnable 实例 run,并使用Lambda表达式。 EasyThreadA::method 绑定到 run 上。然后创建两个线程 a 和 b,分别启动它们,它们会…...

分布式相关理论详解
目录 1.绪论 2.什么是分布式系统,和集群的区别 3.CAP理论 3.1 什么是CAP理论 3.2 一致性 3.2.1 计算机的一致性说明 1.事务中的一致性 2.并发场景下的一致性 3.分布式场景下的一致性 3.2.2 一致性分类 3.2.3 强一致性 1.线性一致性 a) 定义 a) Raft算法…...

Linux基础知识之Shell命令行及终端中的快捷键
1.察看历史命令快捷键 按键 操作 ctrl p 返回上一次输入命令字符 ctrl n 返回下一次输入命令字符 ctrl r 输入单词甚至词组搜索匹配历史命令 alt p 输入字符查找与字符相接近的历史命令 alt . 向之前执行的命令的最后一个参数轮循, 并将之添加到当前光标之后…...
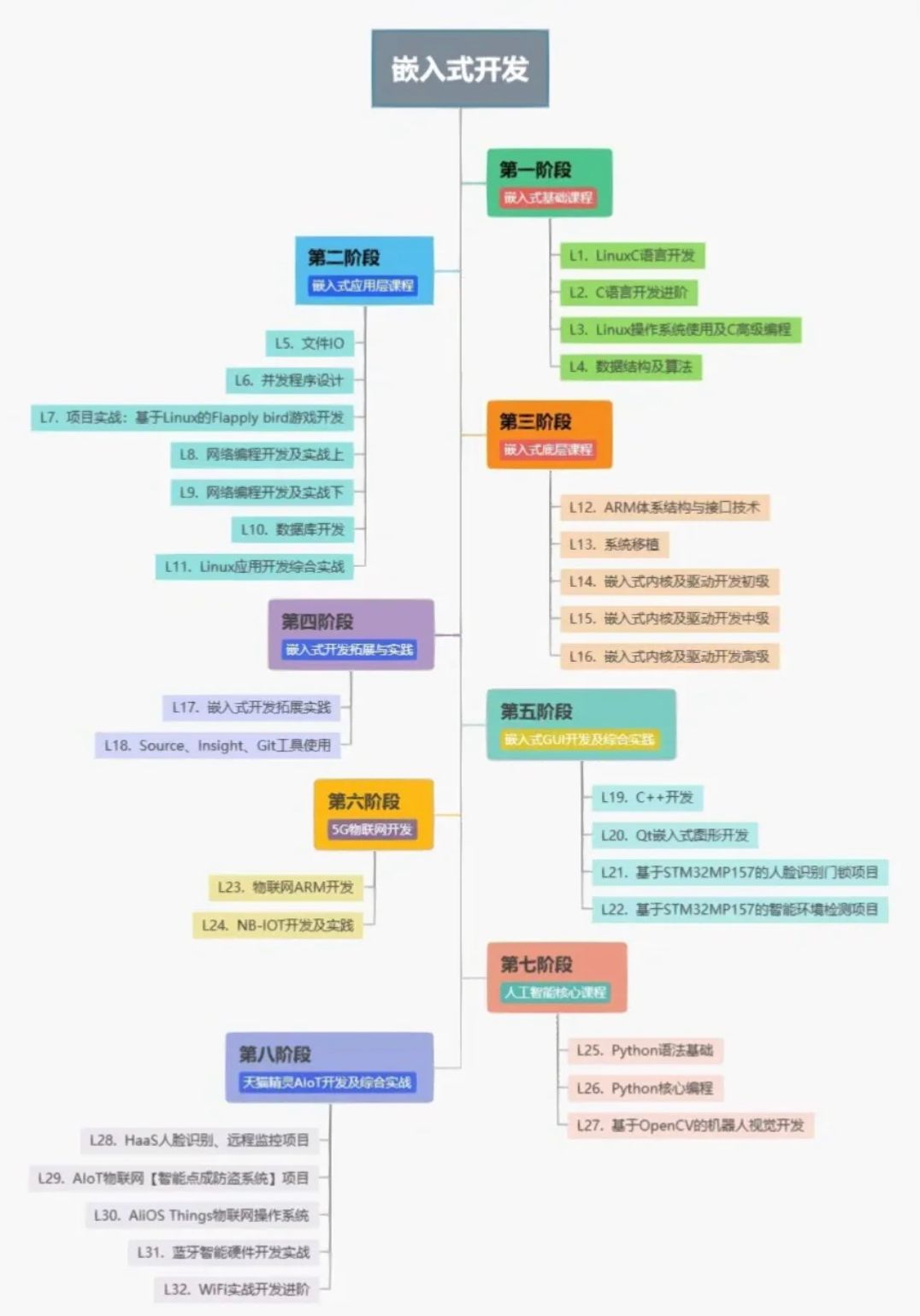
研究生选择学习Android开发的利与弊?
在开始前刚好我有一些资料,是我根据网友给的问题精心整理了一份「Android的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!!产品经理可以学学Axure快…...

怎么评价程序员40岁了竟然还在撸代码?
怎么评价外卖员40岁了竟然还在送外卖? 怎么评价滴滴司机40岁了竟然还在跑滴滴? 怎么评价老师40岁了竟然还在教书?难道程序员的本职工作不是敲代码吗?无论你是管理层还是螺丝钉,工业环境下怎么可能一行代码都不敲呢&…...

SQL优化(一)基础概念
基数(cardinality) 表中某个列的唯一键的数量叫做基数,主键列的基数就是表中数据的总行数。 可以用select count(distinct 列名) from 表名来计算基数。 基数的高低影像列的数据分布。 例如:先用Scott账户创建一个测试表test …...

【C++高阶】哈希:全面剖析与深度学习
目录 🚀 前言一: 🔥 unordered系列关联式容器1.1 unordered_map1.2 unordered_set 二: 🔥 哈希的底层结构 ⭐ 2.1 哈希概念⭐ 2.2 哈希冲突⭐ 2.3 哈希函数⭐ 2.4 哈希冲突解决2.4.1 🌄闭散列2.4.2 &#x…...

PHP西陆招聘求职系统小程序源码
🔥【职场新宠】西陆招聘求职系统,你的职场加速器🚀 🎉【开篇安利:一站式求职新体验】🎉 还在为找工作焦头烂额吗?是时候告别传统招聘网站的繁琐与低效了!今天给大家种草一个超赞的…...

系统移植(十一)根文件系统(未整理)
文章目录 一、根文件系统中各个目录文件功能解析:二、对busybox进行配置和编译(一)执行make help命令获取make的帮助信息(二)对busybox源码进行配置,配置交叉编译器(三)执行make men…...

mac中docker常用命令总结
在Mac中,Docker的常用命令可以总结如下表格: 命令用途docker run运行一个新的容器实例。可以指定镜像名来启动容器,并支持多种参数来调整容器的运行方式。docker ps列出当前正在运行的容器。可以通过添加-a参数来列出所有容器(包…...

Python 【机器学习】 进阶 之 【实战案例】房价数据中位数分析 [ 项目介绍 ] [ 获取数据 ] [ 创建测试集 ]| 1/3(含分析过程)
Python 【机器学习】 进阶 之 【实战案例】房价数据中位数分析 [ 项目介绍 ] [ 获取数据 ] [ 创建测试集 ]| 1/3(含分析过程) 目录 Python 【机器学习】 进阶 之 【实战案例】房价数据中位数分析 [ 项目介绍 ] [ 获取数据 ] [ 创建测试集 ]| 1/3&#x…...

Linux 4: Bash
1 Bash环境 1 命令执行的顺序 1 绝对路径、相对路径 2 alias 3 内置的builtin 4 $PATH找到的第一个命令 2 bash的登录信息,保存在哪里? 保存在/etc/issue. 3 bash的环境配置文件 1 如果是login shell,读以下,有优先级:如果…...

第十四天学习笔记2024.7.25
Git安装 1.安装git 2.创建git仓库 3.创建文件并且提交文件 (git add . 将文件提交到缓存)(git commit -m 说明)(git log 查看历史) 4.分支创建与解决分支冲突问题 创建主机(git 192.1…...

花几千上万学习Java,真没必要!(三十七)
IO 流: 读取数据到内存的过程:可以包括从硬盘、网络或其他存储设备中将数据加载到内存中,以便程序能够访问和处理这些数据。 写入数据到硬盘的过程:通常是将内存中的数据保存到硬盘或其他持久性存储设备中,以便长期存…...
预测模型及其Python和MATLAB实现)
SSA-GRU(自适应平滑自回归门控循环单元)预测模型及其Python和MATLAB实现
SSA-GRU(自适应平滑自回归门控循环单元)预测模型是结合了SSA(Singular Spectrum Analysis,奇异谱分析)和GRU(Gated Recurrent Unit,门控循环单元)模型的一种时间序列预测方法。以下是…...

【ROS】让你的回调函数并行起来
【前言】 众所周知,ROS中的所有回调函数,都由 ros::spin() 这个家伙来统一管理和唤醒。这里说的是所有通过ROS方式创建出来的回调函数,比如ros::Subscriber、ros::Timer等等的回调函数。 【举例】 我们先来看一个示例节点: #i…...

M12电连接器的编码分类及应用领域分析
12电连接器的编码主要包括A、B、C、D、X、S、T、K、L等类型,每种编码都有其特定的应用场景和功能: A编码:适用于传感器、直流电、1G以太网。 B编码:主要用于PROFIBUS总线系统。 C编码:适用于交流电。 D编码&#x…...

基于YOLOv8的道路裂缝坑洼检测系统
基于YOLOv8的道路裂缝坑洼检测系统 (价格88) 包含 【“裂缝”,“凹坑”】 2个类 通过PYQT构建UI界面,包含图片检测,视频检测,摄像头实时检测。 (该系统可以根据数据训练出的yolov8的权重文件,运用在其他检测系…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
