相似度计算方法
一、相似度计算方法
相似度算法是计算两个或多个对象之间相似程度的方法,这些对象可以是文本、图像、音频等不同类型的数据。在计算机科学、信息检索、推荐系统、数据挖掘等领域中,相似度算法具有广泛的应用。

二、应用场景
- 搜索引擎:用于文本相似度计算,改善搜索结果的相关性。
- 推荐系统:基于用户行为和兴趣相似度计算,提供个性化推荐。
- 图像识别:比较图像的相似度,用于图像搜索和匹配。
- 音频处理:用于语音识别和声音相似性比较。
三、距离函数
3.1 明可夫斯基(Minkowski)距离
对于任意样本对象 P = [ p 1 , p 2 , . . . , p n ] P=[p_1,p_2,...,p_n] P=[p1,p2,...,pn]与 Q = [ q 1 , q 2 , . . . , q n ] Q=[q_1,q_2,...,q_n] Q=[q1,q2,...,qn],它们之间的距离定义为
d ( P , Q ) = ( ∑ i = 1 n ( p i − q i ) 2 ) 1 k d(P, Q) = ({\sum_{i=1}^{n} (p_i - q_i)^2} )^{\frac{1}{k}} d(P,Q)=(i=1∑n(pi−qi)2)k1
当 k = 1 k=1 k=1时,即为曼哈顿(Manhattan)距离(L1距离),在某些特定的机器学习场景中,如Lasso回归(L1正则化),曼哈顿距离(或L1范数)被用作正则化项,以促进稀疏解的产生。定义如下:
d ( P , Q ) = ∑ i = 1 n ∣ p i − q i ∣ d(P, Q) = {\sum_{i=1}^{n} |p_i - q_i}| d(P,Q)=i=1∑n∣pi−qi∣
当 k = 2 k=2 k=2时,即为欧氏(Euclidean)距离(L2距离), 在聚类算法(如K-means)、分类算法(如K-NN)中,欧氏距离常被用作衡量样本之间相似度的指标。定义如下:
d ( P , Q ) = ∑ i = 1 n ( p i − q i ) 2 d(P, Q) = \sqrt {\sum_{i=1}^{n} (p_i - q_i)^2} d(P,Q)=i=1∑n(pi−qi)2
当 k = ∞ k=\infty k=∞时,即为切比雪夫(Chebyshev)距离:
d ( P , Q ) = max ∣ ( p i − q i ) ∣ ( 1 ⩽ i ⩽ n ) d(P, Q) =\max|(p_i - q_i)| (1⩽i⩽n) d(P,Q)=max∣(pi−qi)∣(1⩽i⩽n)
3.2 马氏(Mahalanobis)距离
Mahalanobis距离考虑了属性之间的相关性,可以更加准确地衡量多维数据之间的距离。Mahalanobis距离是对Minkowski距离的改进,对于一切线性变换是不变的,克服了Minkowski距离受量纲影响的缺点,也部分地克服了多重相关性。Mahalanobis距离在分类算法中比较常用,但不足在于协方差矩阵难以确定,计算量比较大,不适合大规模数据集。公式如下:
d = ( p − q ) T A − 1 ( p − q ) d=(p-q)^TA^{-1}(p-q) d=(p−q)TA−1(p−q)
其中, A A A为 n × n n×n n×n的协方差矩阵, A − 1 A^{−1} A−1为协方差矩阵的逆。
3.3 汉明(Hamming)距离
汉明距离是指两个等长字符串在对应位置上不同字符(或比特)的数量。简单来说,它表示将一个字符串转换成另一个字符串所需替换的字符数。
d ( a , b ) = ∑ i = 1 n ( a i ≠ b i ) d(a,b)=\sum_{i=1}^{n}(a_i \neq b_i) d(a,b)=i=1∑n(ai=bi)
其中, n n n是字符串的长度, a i a_i ai和 b i b_i bi分别表示字符串 a a a和 b b b中第 i i i个位置的字符。如果 a i a_i ai和 b i b_i bi不相等,则求和项为1;否则为0。最终求和的结果即为两个字符串的汉明距离。例如,在特征匹配算法中,可以将图像的特征描述为二进制字符串,并使用汉明距离来衡量不同特征之间的相似度。
四、相似度(系数)
4.1 余弦相似度(Cosine Similarity)
余弦相似度是通过计算两个向量在多维空间中的夹角余弦值来评估它们的相似度。余弦相似度的取值范围是[-1, 1],夹角越小(即余弦值越接近于1),两个向量越相似。
cos ( θ ) = a ⋅ b ∥ a ∥ ∥ b ∥ = ∑ i = 1 n ( a i b i ) ∑ i = 1 n a i 2 ∑ i = 1 n b i 2 \cos(\theta) = \frac{a \cdot b}{\|a\| \|b\|} = \frac{\sum_{i=1}^{n} (a_i b_i)}{\sqrt{\sum_{i=1}^{n} a_i^2} \sqrt{\sum_{i=1}^{n} b_i^2}} cos(θ)=∥a∥∥b∥a⋅b=∑i=1nai2∑i=1nbi2∑i=1n(aibi)
其中, a ⋅ b a⋅b a⋅b 表示向量 a a a和向量 b b b的内积, ∣ ∣ a ∣ ∣ ||a|| ∣∣a∣∣和 ∣ ∣ b ∣ ∣ ||b|| ∣∣b∣∣ 分别表示向量 a a a和向量 b b b的模(长度)
4.2 皮尔逊相关系数(Pearson Correlation Coefficient)
相关系数是对向量做标准差、标准化后的夹角余弦,表示两个向量的线性相关程度。
用于度量两个变量X和Y之间的相关(线性相关),其值介于-1与1之间。皮尔逊相关系数具有平移不变性和尺度不变性,计算出了两个向量(维度)的相关性。
C o r r ( p , q ) = ∑ i n ( ( p i − p ˉ ) × ( q i − q ˉ ) ) ( ∑ i n ( p i − p ˉ ) 2 × ∑ i n ( q i − q ˉ ) 2 ) Corr(p,q)=\frac{\sum_{i}^{n}((p_i-\bar{p})\times(q_i-\bar{q}))}{\sqrt{(\sum_{i}^{n}(p_i-\bar{p})^2\times\sum_{i}^{n}(q_i-\bar{q})^2)}} Corr(p,q)=(∑in(pi−pˉ)2×∑in(qi−qˉ)2)∑in((pi−pˉ)×(qi−qˉ))
其中, n n n是样本量, p i p_i pi和 q i q_i qi分别是两个变量的第 i i i个特征值, p ‾ \overline{p} p和 q ‾ \overline{q} q分别是 p p p和 q q q的样本均值。
4.3 杰卡德相似系数(Jaccard Similarity Coefficient)
广义Jaccard系数又称为Tanimoto系数,用 E J EJ EJ表示,广泛用于信息检索和生物学分类中,在二次元性情况下简化为Jaccard系数。
E J ( p , q ) = ∑ i n p i × q i ∑ i n ( p i 2 ) ∑ i n ( q i 2 ) − ∑ i n ( p i × q i ) EJ(p,q)=\frac{\sum_{i}^{n}p_i\times q_i}{\sum_{i}^{n}({p_i}^2)\sum_{i}^{n}({q_i}^2)-\sum_{i}^{n}(p_i\times q_i)} EJ(p,q)=∑in(pi2)∑in(qi2)−∑in(pi×qi)∑inpi×qi
4.4 KL散度
KL散度(Kullback-Leibler Divergence),即相对熵,是衡量两个分布(P、Q)之间的距离,计算出的距离越小越相似。
D K L ( p ∣ ∣ q ) = ∑ i = 1 n p i l o g p i q i D_{KL}(p||q)=\sum_{i=1}^{n}p_i log\frac{p_i}{q_i} DKL(p∣∣q)=i=1∑npilogqipi
表示的就是概率 q q q 与概率 p p p 之间的差异,很显然,散度越小,说明概率 q q q 与概率 p p p 之间越接近,那么估计的概率分布于真实的概率分布也就越接近。
4.5 结构相似性指数(Structural Similarity Index, SSIM)
结构相似性指数(Structural Similarity Index, SSIM)是一种用于衡量两幅图像之间相似度的指标。它通过比较图像的亮度、对比度和结构信息来确定两幅图像之间的相似程度。SSIM指数的取值范围是0到1之间,其中:1表示两幅图像完全相同,0表示两幅图像差异极大。
SSIM主要由以下三个方面组成:
- 亮度相似度(Luminance Similarity):反映了两幅图像的亮度信息是否一致。
- 对比度相似度(Contrast Similarity):反映了两幅图像的对比度信息是否一致。
- 结构相似度(Structure Similarity):反映了两幅图像的结构信息是否一致。
SSIM的计算公式为:
SSIM ( x , y ) = ( 2 μ x μ y + c 1 ) ( 2 σ x y + c 2 ) ( μ x 2 + μ y 2 + c 1 ) ( σ x 2 + σ y 2 + c 2 ) \text{SSIM}(x,y) = \frac{(2\mu_x\mu_y + c_1)(2\sigma_{xy} + c_2)}{(\mu_x^2 + \mu_y^2 + c_1)(\sigma_x^2 + \sigma_y^2 + c_2)} SSIM(x,y)=(μx2+μy2+c1)(σx2+σy2+c2)(2μxμy+c1)(2σxy+c2)
其中, x x x 和 y y y 是待比较的两幅图像, μ x \mu_x μx 和 μ y \mu_y μy 分别是 x x x 和 y y y 的均值, σ x \sigma_x σx 和 σ y \sigma_y σy 分别是 x x x 和 y y y 的标准差, σ x y \sigma_{xy} σxy 是 x x x 和 y y y 的协方差。 c 1 c_1 c1 和 c 2 c_2 c2 是两个常数,用于避免分母为0,并调整结构相似度的范围。
相关文章:

相似度计算方法
一、相似度计算方法 相似度算法是计算两个或多个对象之间相似程度的方法,这些对象可以是文本、图像、音频等不同类型的数据。在计算机科学、信息检索、推荐系统、数据挖掘等领域中,相似度算法具有广泛的应用。 二、应用场景 搜索引擎:用于文…...

Vue 点击markdown页内链接,路由设置不跳转
在路由index.js里添加路由守卫: router.beforeEach((to,from,next)>{//如果是md页内链接“#xxx”,则不跳转const hash window.location.hash;if(hash.startsWith(#)) {next(false);}else{...其他控制代码next();} });当markdown用[标题链接](#标题名…...

IOday4
一、思维导图 二、练习 1、使用父子进程完成两个文件的拷贝,父进程拷贝前一半内容,子进程拷贝后一半内容,子进程结束后退出,父进程回收子进程的资源 #include<myhead.h> int main(int argc, const char *argv[]) {//判断终…...

智能座舱背后主流车机平台(SA8155/SA8295)的高通Hexagon DSP是什么?
智能座舱背后主流车机平台(SA8155/SA8295)的高通Hexagon DSP是什么? 一、高通Hexagon DSP的辉煌发展历程 高通,作为全球领先的无线通信技术创新者,其处理器技术一直走在行业前列。随着智能手机和物联网设备的普及,对处理器性能的…...

linux进程控制——进程等待——wait、waitpid
前言:本节内容仍然是进程的控制,上一节博主讲解的是进程控制里面的进程创建、进程退出、终止。本节内容将讲到进程的等待——等待是为了能够将子进程的资源回收,是父进程等待子进程。 我们前面的章节也提到过等待, 那里的等待是进…...

Shell脚本的进程管理
进程管理是系统管理的重要方面,通过对进程的监控、启动、停止和重启,可以保证系统的稳定运行。Shell脚本是一种强大的工具,可以对进程进行自动化管理,提高效率和准确性。 参考:shell脚本进程管理 - CSDN文库 shell脚本…...

JLink烧录失败
1. 现象: 这个位置是灰色的,没有SW Device信息。 MDK下面的打印: J-Flash的打印: windows上面的弹框的现象没有截屏。 2. 解决办法: 1.打开J-Link Commander,输入unlock kinetis,看现象不起作用,网…...

Monorepo简介
Monorepo 第一章:与Monorepo的邂逅第二章:Multirepo的困境第三章:Monorepo的魔力 - 不可思议的解决问题能力第四章:Monorepo的挑战与应对策略第五章:总结第六章:参考 第一章:与Monorepo的邂逅 …...

SpringBoot打包为jar包,打包前注意事项及打包教程
在打包 Spring Boot 项目为 JAR 包之前,有一些重要的注意事项和步骤,以确保打包过程顺利并生成一个可正常运行的 JAR 包: 1. 检查依赖和版本 确保所有依赖项和插件版本是最新且兼容的,特别是 Spring Boot 版本和其相关依赖的版本…...

B端系统UI个性化设计:感受定制之美
B端系统UI个性化设计:感受定制之美 引言 艾斯视觉作为ui设计和前端开发从业者,其观点始终认为:在当今竞争激烈的商业环境中,B端(Business-to-Business)系统的设计不再仅仅是功能性的堆砌,而是…...

前端常用 utils 工具封装
// 函数防抖 export function debounce(fn, interval) {let timerreturn function (this, ...args) {clearTimeout(timer)const context thislet params [...args]timer setTimeout(() > {fn.call(context, ...params)}, interval || 1000)} }// 函数节流 export functio…...

项目都做完了,领导要求国际化????--JAVA后端篇
springboot项目国际化相信各位小伙伴都会,很简单,但是怎么项目都做完了,领导却要求国际化文件就很头疼了 国际化的SpringBoot代码: 第一步:创建工具类 /*** 获取i18n资源文件** author bims*/ public class Message…...

国内备受好评PostgreSQL数据库性能如何?
为什么国内很多数据库采用PostgreSQL数据库作为基础,再次开发自己的产品呢?不仅仅是因为PostgreSQL数据库开源免费、PostgreSQL 数据库的性能也是相当出色的,具有以下几个方面的特点: 1. 处理大规模数据: - 能够有效地管理和处…...

彻底搞懂前端跨域解决方案
一、浏览器的同源策略 1、同源策略概述 同源策略是浏览器为确保资料安全,而遵循的一种策略,该策略对访问资源进行了一些限制。 2、什么是源(origin)? 3、示例 4、同源请求 5、非同源请求 二、跨域会受到哪些限制 1…...
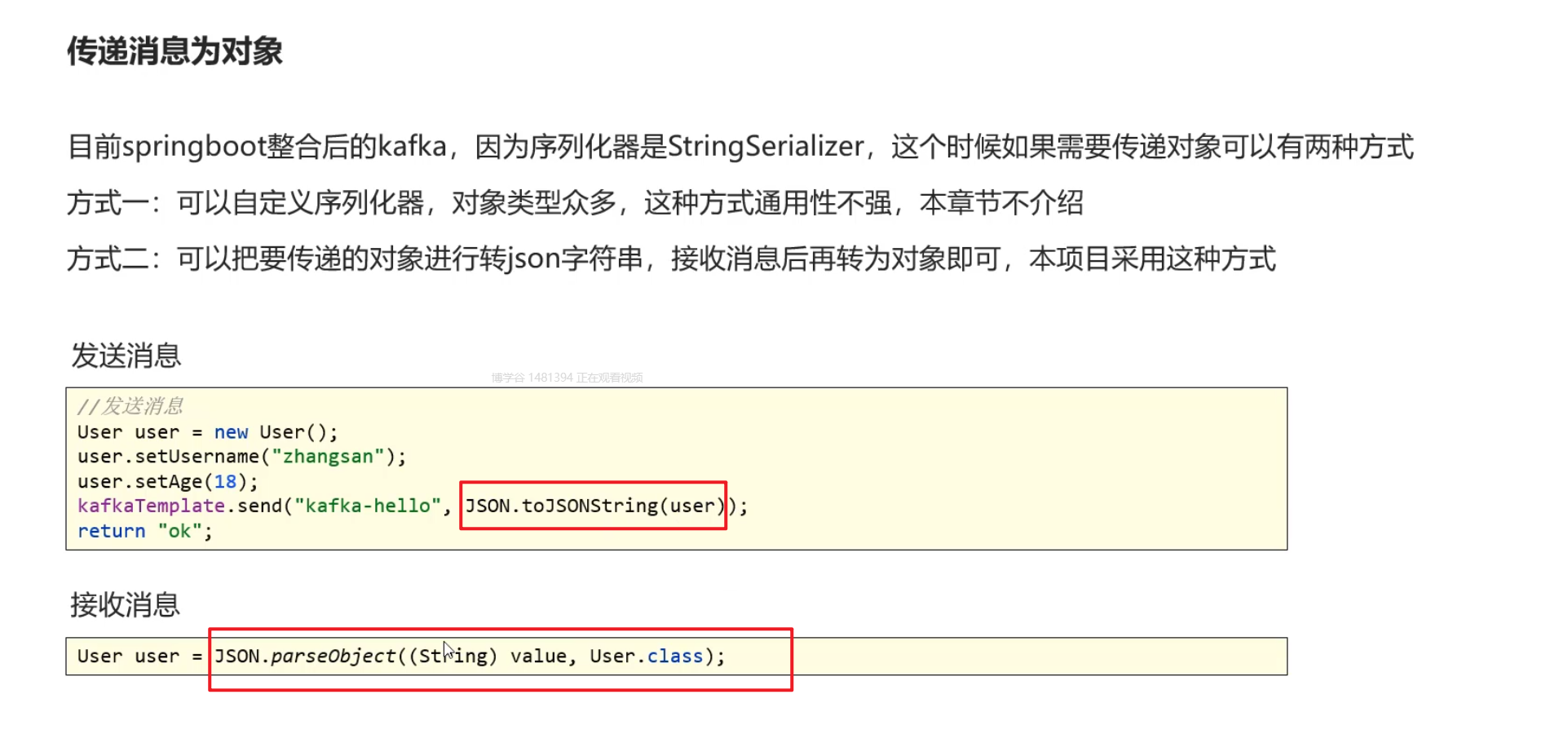
Kafka基础概念
MQ消息中间件 1)总览: 消息中间件 这里我们主要学习的是kafka的基础概念 具体参考黑马头条:https://www.bilibili.com/video/BV1Qs4y1v7x4/?spm_id_from333.337.search-card.all.click 2)消息中间件对比 3)Kafka介…...
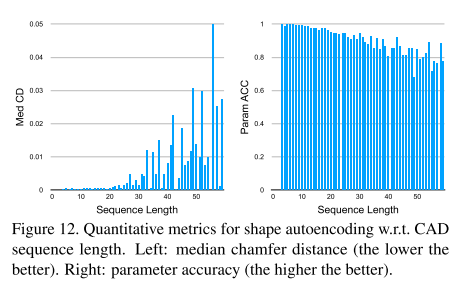
【论文阅读笔记】DeepCAD: A Deep Generative Network for Computer-Aided Design Models
1 引言 现有3D生成模型: 3D点云:大量离散的3D点组成的数据表示形式; 多边形网格:一系列相连的多边形组成的3D模型; 水平集场:使用数值函数来表示物体的边界,并根据函数值的正负来确定物体内部…...

《如鸢》开通官号,女性向游戏爆款预定
今天,备受瞩目的沉浸式剧情卡牌手游《如鸢》正式开通了官方社媒账号并发布了玩家信。 《如鸢》由灵犀互娱倾力打造,游戏不仅拥有跌宕起伏的权谋剧情,更采用Live2D技术,为玩家带来沉浸式的游戏体验,吸引了众多玩家关注。…...

OpenAI再下一城:发布Voice Engine,可使用文本和参考语音合成说话者的新语音!
转自 机器学习算法工程师 OpenAI又发布了一个最新的工作:Voice Engine。Voice Engine可以使用文本输入和单个 15 秒音频样本生成听起来自然且与原始说话者非常相似的语音。而且,一个小型模型仅通过一个 15 秒的样本就能创造出富有情感且逼真的语音。Voi…...

KVM高级功能部署
一、概述 KVM(Kernel-based Virtual Machine)是一种基于内核的虚拟化技术,它依赖于CPU的虚拟化扩展(如Intel VT和AMD-V)来实现虚拟机的创建、管理和调度。KVM虚拟化技术因其高效、稳定的特点,在云计算和企…...
)
【C语言】柔性数组(打开前所未见的大门)
文章目录 前言柔性数组1.1 概念1.2 柔性数组的特点1.3 柔性数组的使用1.4 柔性数组的优势 总结 前言 说到柔性数组,相信有很多学过C语言的读者都不知道这是个什么东西。不过没有关系,相信本章能够带你从到认识到掌握柔性数组,做一个充满知识…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
