线性代数之矩阵
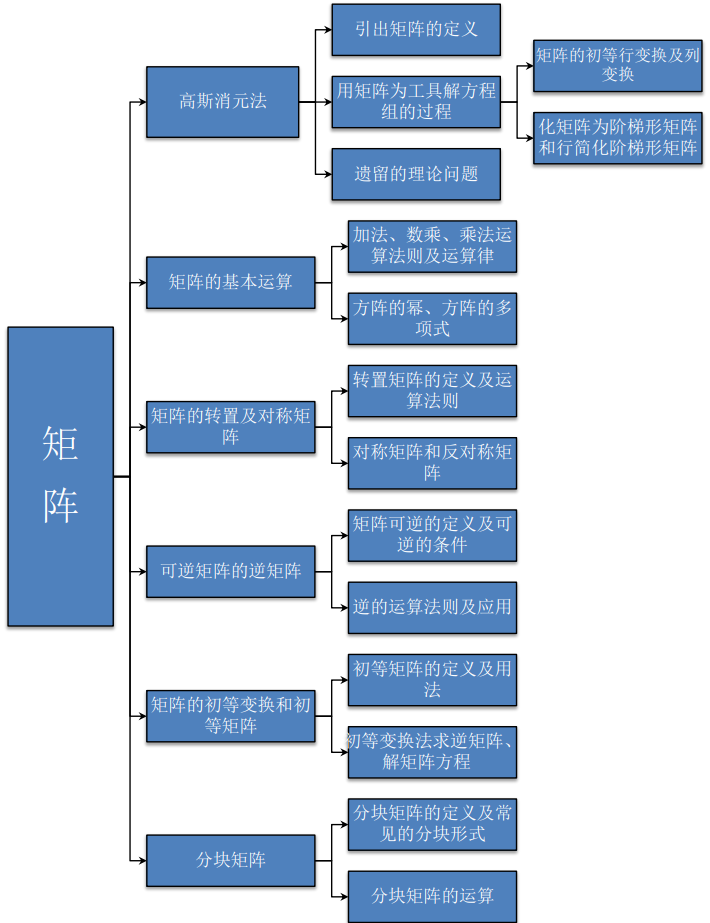
一、思维导图
二、矩阵及其运算
1、矩阵的定义

注:

零矩阵:元素均为0 的矩阵,通常记作0
m*n称为矩阵的类型。
满足阶梯形矩阵
行简化的阶梯形矩阵即满足如下条件的矩阵: (1)阶梯形; (2)非零首元所在列其余元素均为0 ; (3) 非零首元均是1.

2、运算法则
2.1 矩阵加法

2.2 矩阵的数量乘法

2.3 矩阵的乘积
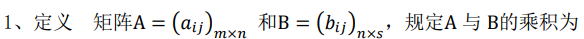

3、几个特别的矩阵
3.1 𝑛阶单位矩阵
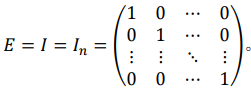
3.2 𝑛阶数量矩阵
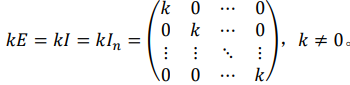
3.3 对角矩阵

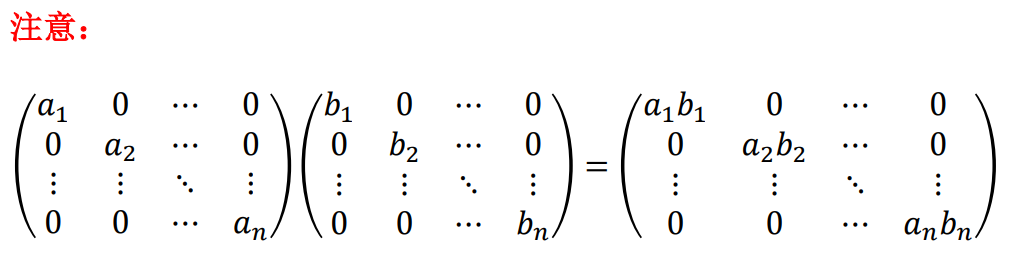
3.4 上(下)三角矩阵


3.5 结论

4、定理 若矩阵𝑨,𝑩为同阶方阵,则 𝑨𝑩 = |𝑨 | | �� |。
5、方阵的幂和方阵的多项式

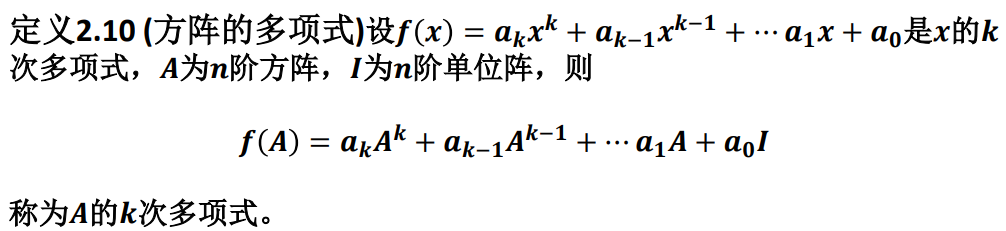

6、转置与对称




7、可逆矩阵
7.1 逆矩阵

定理 若𝑨是可逆矩阵,则𝑨的逆矩阵是唯一的
7.2 伴随矩阵


7.3 运算律

三、矩阵的初等变换和初等矩阵
1、初等变换

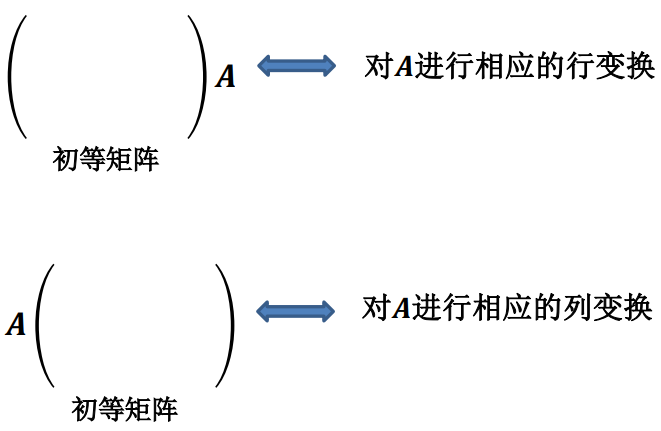
2、初等矩阵
初等矩阵:单位矩阵经过一次初等变换所得到的矩阵



作用
3、初等变换法求逆矩阵

4、初等变换法解矩阵方程


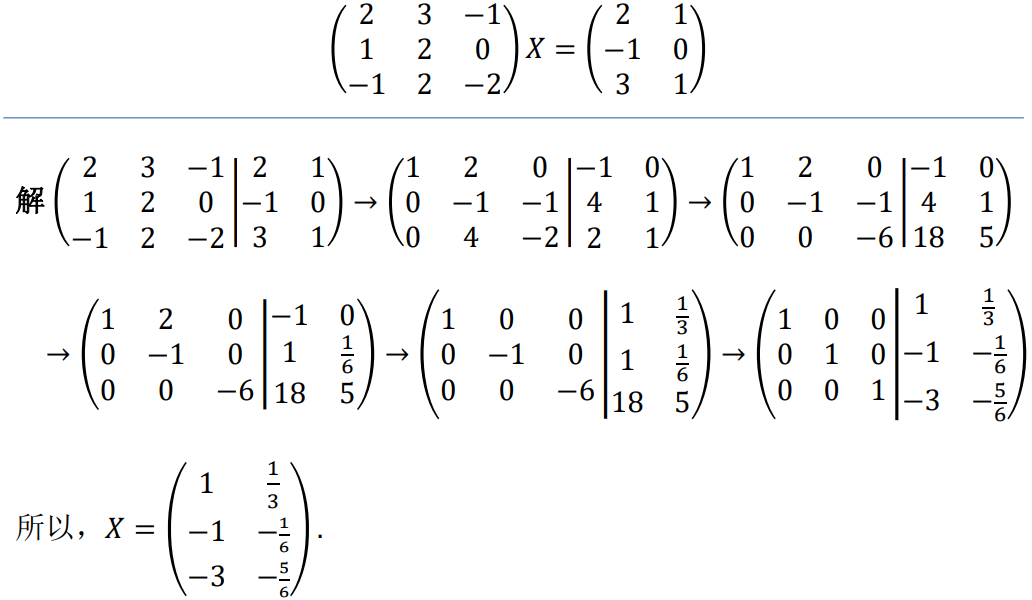

四、复习题

相关文章:

线性代数之矩阵
一、思维导图二、矩阵及其运算1、矩阵的定义注:零矩阵:元素均为0 的矩阵,通常记作0m*n称为矩阵的类型。满足阶梯形矩阵 行简化的阶梯形矩阵即满足如下条件的矩阵: (1)阶梯形; (2)非零首元所在列其余元素均为0 ; (3) 非…...

【个人首测】百度文心一言 VS ChatGPT GPT-4
昨天我写了一篇文章GPT-4牛是牛,但这几天先别急,文中我测试了用GPT-4回答ChatGPT 3.5 和 Notion AI的问题,大家期待的图片输入也没有出现。 昨天下午百度发布了文心一言,对标ChatGPT,录屏无实机演示让百度股价暴跌。但是晚上百度就…...
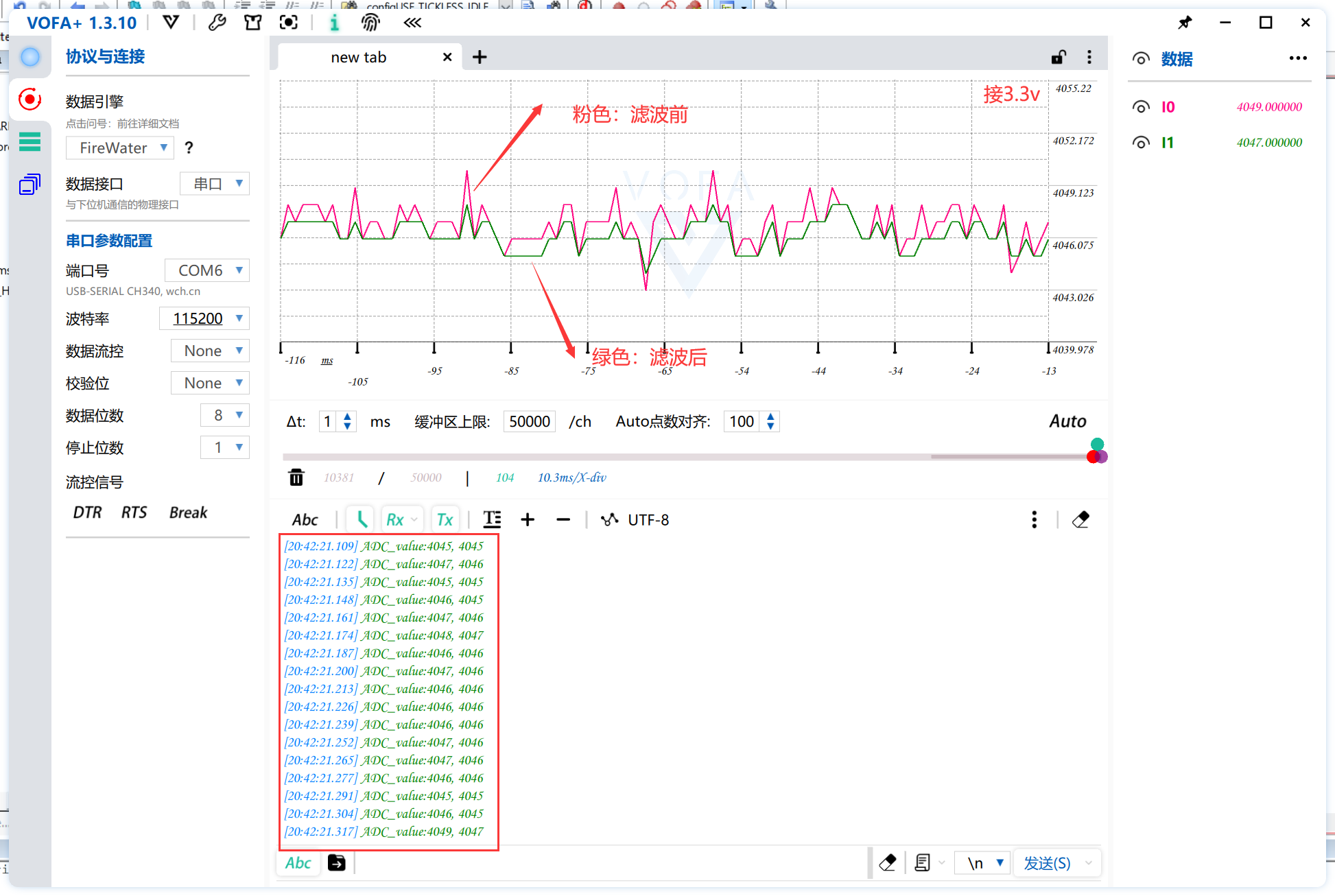
基于STM32的ADC采样及各式滤波实现(HAL库,含VOFA+教程)
前言:本文为手把手教学ADC采样及各式滤波算法的教程,本教程的MCU采用STM32F103ZET6。以HAL库的ADC采样函数为基础进行教学,通过各式常见滤波的实验结果进行分析对比,搭配VOFA工具直观的展示滤波效果。ADC与滤波算法都是嵌入式较为…...
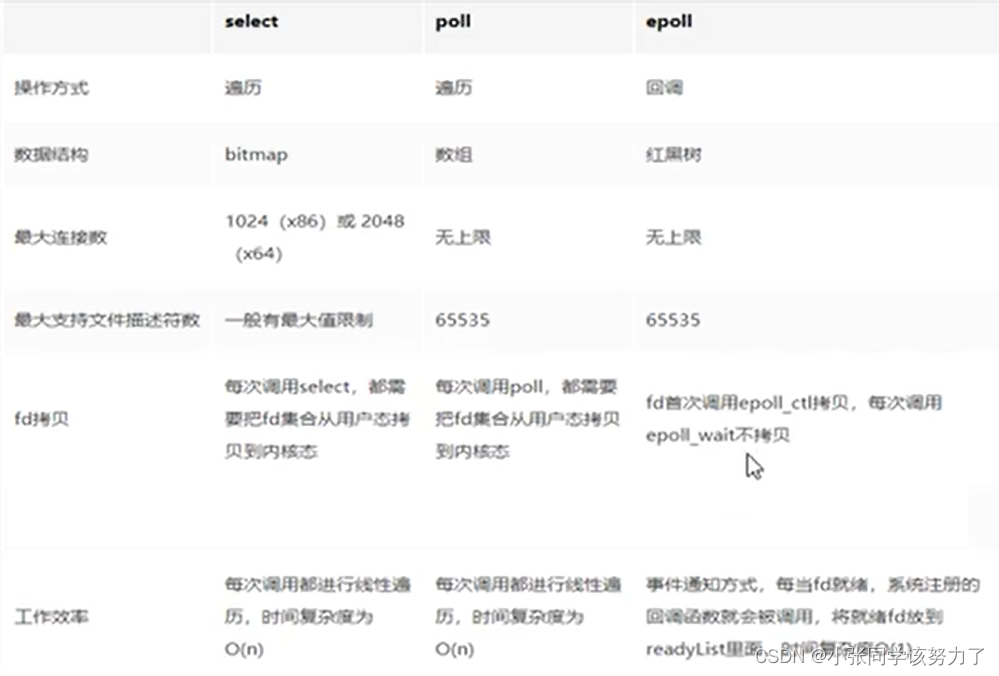
Redis高级篇
文章目录面试题库redis有哪些用法?redis单线程时代性能依然很快的原因?主线程和IO线程怎么协作完成请求处理的BigKey(重要)什么算是BigKey?怎么发现BigKey?怎么删除bigkey?bigkey生产调优缓存双…...
这句话一般是干什么的,在代码中可以不加么?)
sess.close()这句话一般是干什么的,在代码中可以不加么?
sess.close()这句话是用于关闭TensorFlow会话对象的方法。 关闭会话对象可以释放资源,避免内存泄漏,以及清除图中的变量和操作。 在代码中是否可以不加这句话,取决于你是如何创建和使用会话对象的。如果你使用了with语句来创建和管理会话对…...

网络舆情监测处置平台,TOOM舆情如何做好舆情风险点及防控措施?
网络舆情监测处置平台是一个综合性的系统,旨在帮助企业、政府或其他组织有效地管理和处置网络舆情。从多个角度来分析该平台,我们可以考虑以下几个方面: 1,技术实现 网络舆情监测处置平台的技术实现是其核心,它通常采…...
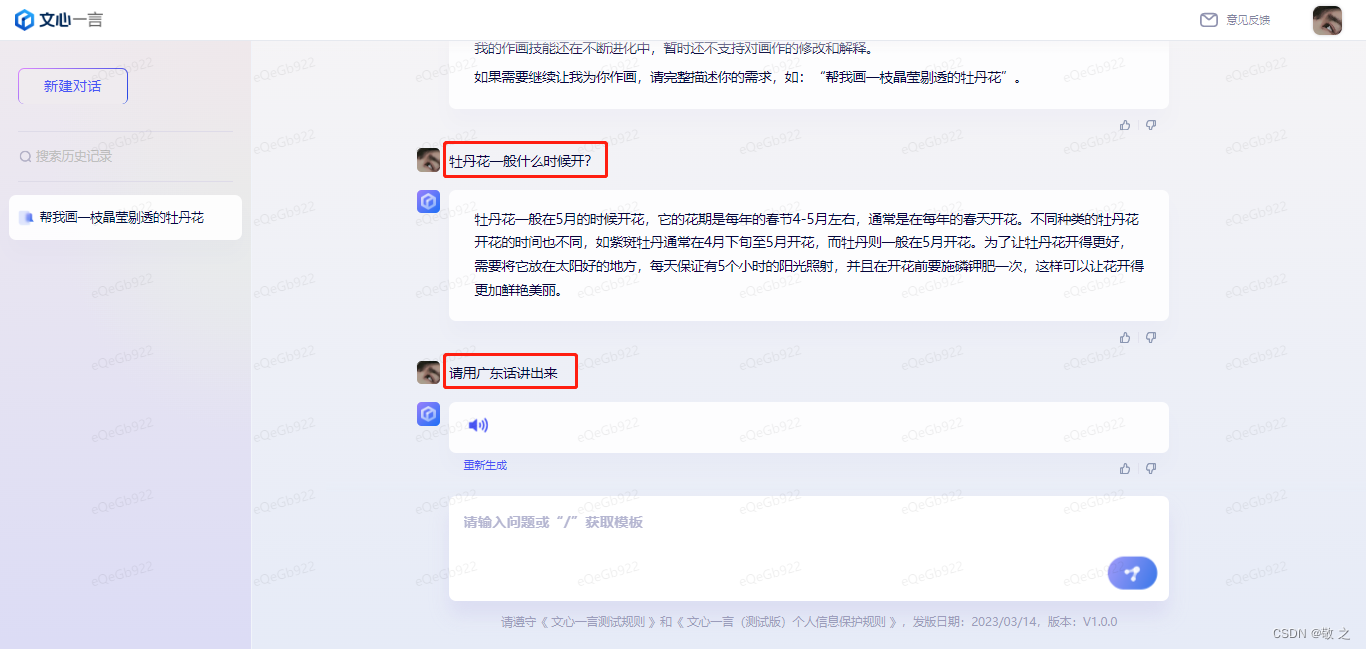
百度文心一言对标 ChatGPT,你怎么看?
文心一言 VS ChatGPT接受不完美 期待进步里程碑意义文心一言初体验✔ 文学创作✔ 商业文案创作✔ 数理逻辑推算✔ 中文理解✔ 多模态生成写在最后何为文心?“文”就是我们中华语言文字中的文,“心”是希望该语言模型可以用心的去理解语言,用心…...

阿里笔试2023-3-15
太菜了,记录一下笔试题目,代码有更好解法欢迎分享。 1、满二叉子树的数量。 给定一颗二叉树,试求这课二叉树有多少个节点满足以该节点为根的子树是满二叉树?满二叉树指每一层都达到节点最大值。 第一行输入n表示节点数量ÿ…...
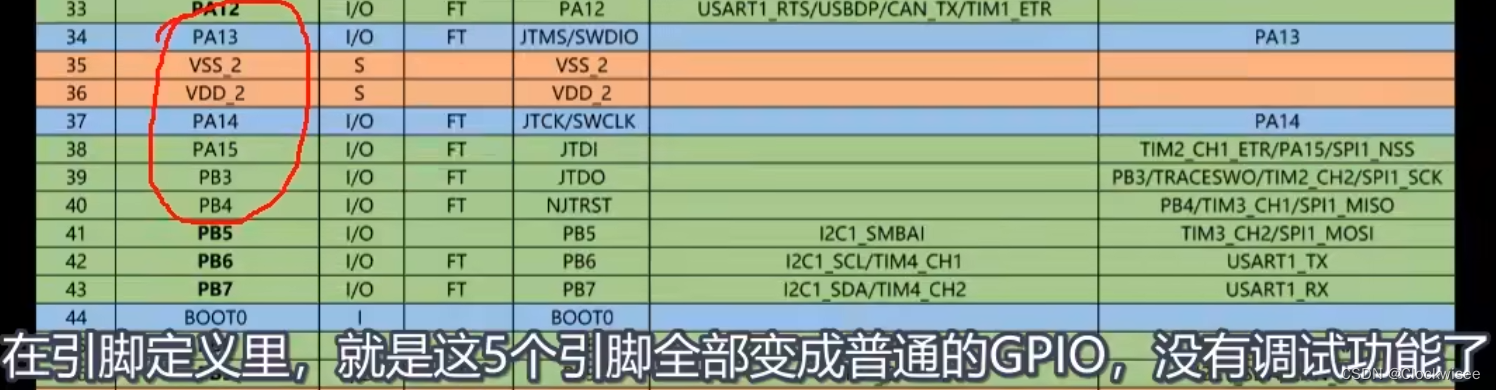
STM32:TIM定时器输出比较(OC)
一、输出比较简介 1、输出比较 OC(Output Comapre)输出比较输出比较可以通过比较CNT(时基单元)和CCR(捕获单元)寄存器值的关系,来对输出电平进行置1、置0或翻转的操作,用于输出一定频…...

HTTPS 加密协议
✏️作者:银河罐头 📋系列专栏:JavaEE 🌲“种一棵树最好的时间是十年前,其次是现在” 目录HTTPS"加密" 是什么HTTPS 的工作过程引入证书HTTPS http 安全层 (SSL) SSL 用来加密的协议,也叫 TLS …...

分布式锁和分布式事务
分布式锁 没有图形,只通过大量文字进行说明。分布式锁:redis分布式锁, zk分布式锁, 数据库做分布式锁 redis分布式锁 setnx key value ex 10 原子操作 AB两个线程减库存业务,假设库存是10 A线程获取锁,…...

RK3568平台开发系列讲解(驱动基础篇)I2C协议介绍
🚀返回专栏总目录 文章目录 一、I2C基本读写过程二、通讯的起始和停止信号三、数据有效性四、地址及数据方向五、响应沉淀、分享、成长,让自己和他人都能有所收获!😄 📢I2C的协议定义了通讯的起始和停止信号、数据有效性、响应、仲裁、时钟同步和地址广播等环节。 一、…...

HTML 音频(Audio)
HTML 音频(Audio) 声音在HTML中可以以不同的方式播放. 问题以及解决方法 在 HTML 中播放音频并不容易! 您需要谙熟大量技巧,以确保您的音频文件在所有浏览器中(Internet Explorer, Chrome, Firefox, Safari, Opera)和所有硬件上…...
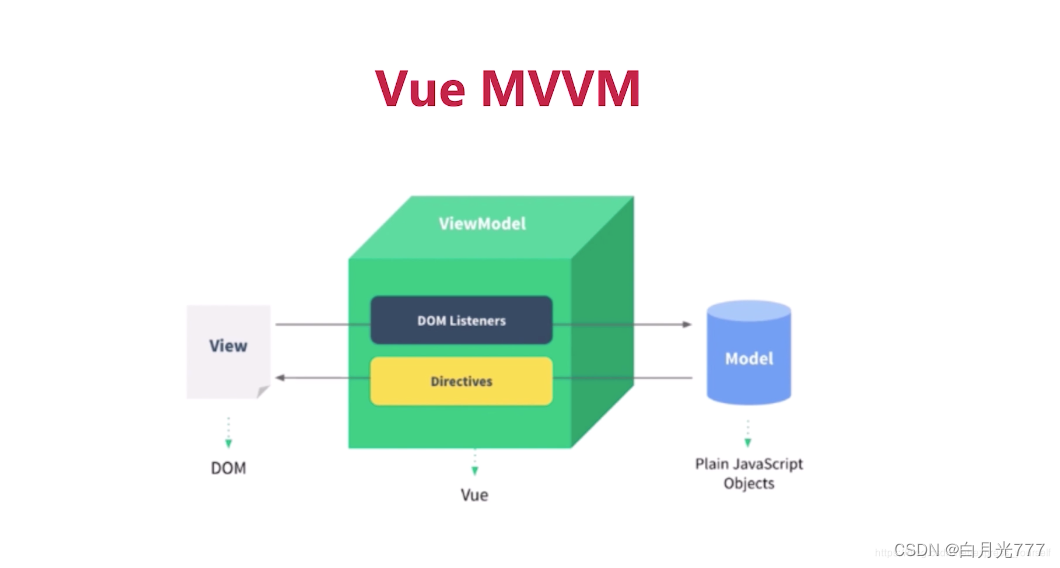
什么是Vue
✅作者简介:CSDN一位小博主,正在学习前端,欢迎大家一起来交流学习🏆 📃个人主页:白月光777的CSDN博客 🔥系列专栏:Vue从入门到进阶 💬个人格言:但行好事&…...

python 内置函数和多线程
以下是Python的一些内置函数。这些函数是Python语言提供的基本功能,可以在不需要导入任何其他模块的情况下直接使用。这些函数可以完成广泛的任务,例如数学运算,序列和集合操作,类型转换,文件操作等等。透彻理解这些函…...

【Spring】我抄袭了Spring,手写一套MySpring框架。。。
这篇博客实现了一个简单版本的Spring,主要包括Spring的Ioc和Aop功能 文章目录这篇博客实现了一个简单版本的Spring,主要包括Spring的Ioc和Aop功能🚀ComponentScan注解✈️Component注解🚁在spring中ioc容器的类是ApplicationConte…...
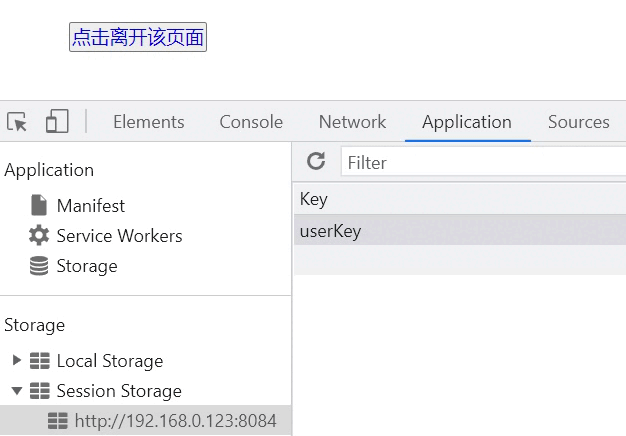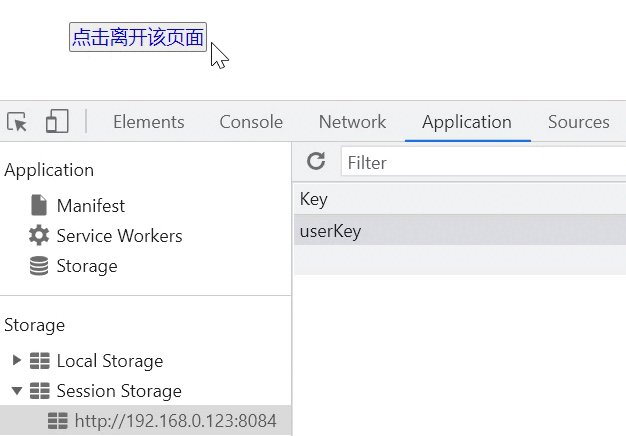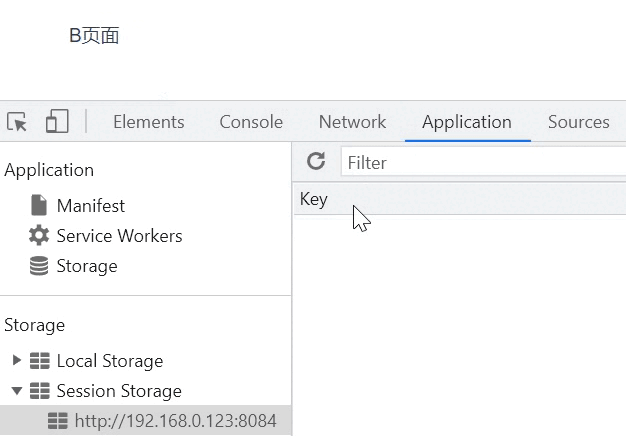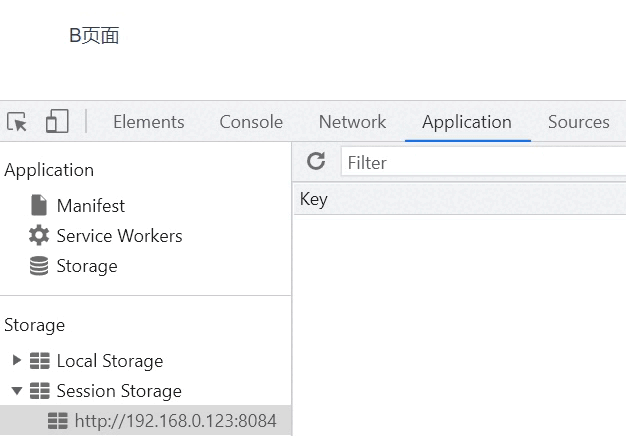
vue中的生命周期
前言 很多时候我们希望能在 vue 生命周期的过程中执行一些操作,生命周期钩子函数也因此诞生了。相信使用过 vue 框架的同学都知道,生命周期的钩子函数允许我们在实例的不同阶段执行各种操作,便于我们更好的控制和使用实例。 生命周期钩子函数…...
)
硬件原理图设计规范(二)
1、可编程逻辑器件 编号 级别 条目内容 备注 1 推荐 FPGA的LE资源利用率要保证在50%~80%之间,EPLD的MC资源的利用率要保证在50%~90%之间。对于FPGA中的锁相环、RAM、乘法器、DSP单元、CPU核等资源,经过精确预算,…...

复旦微ZYNQ7020全国产替代方案设计
现在国产化进度赶人,进口的芯片只做了个功能验证,马上就要换上国产的。国内现在已经做出来zynq的只有复旦微一家,已经在研制的有上海安路,还有成都华微(不排除深圳国威也在做,毕竟这个市场潜力很大…...
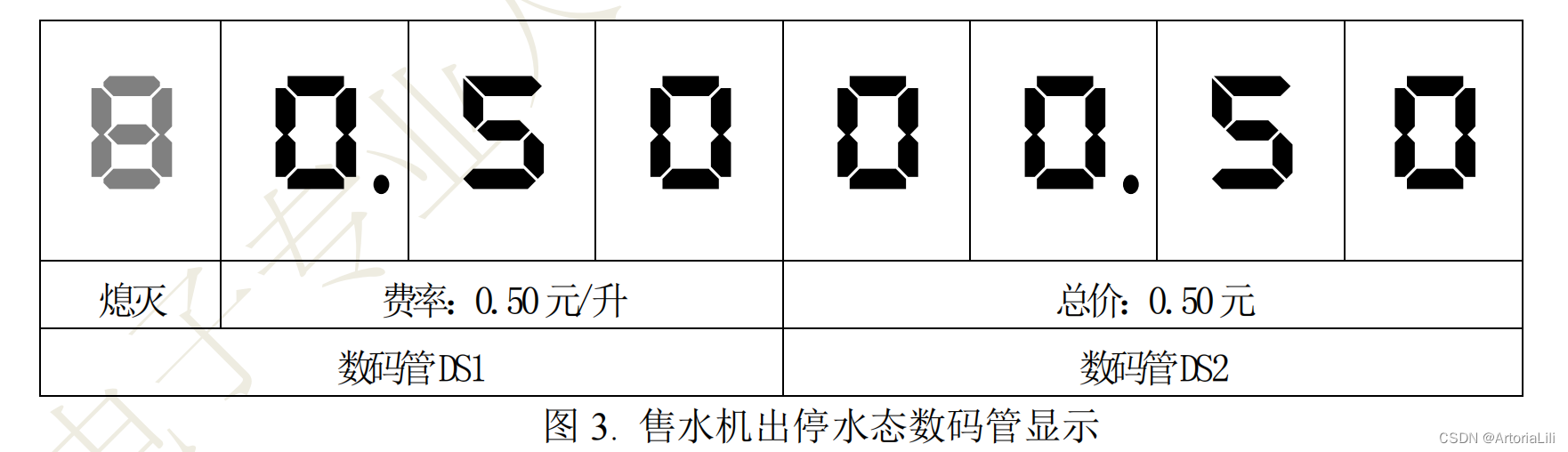
蓝桥杯真题——自动售水机
2012年第四届全国电子专业人才设计与技能大赛“自动售水机”设计任务书1. 系统框图接下来我们将任务分块: 1. 按键控制单元 设定按键 S7 为出水控制按键,当 S7 按下后,售水机持续出水(继电器接通,指示 灯 L10 点亮&…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...
