【数据结构进阶】手撕红黑树

🔥个人主页： Forcible Bug Maker
🔥专栏： C++ || 数据结构

🌈前言

本篇博客主要内容：红黑树的介绍，以及底层代码逻辑和实现。

刚刚接触编程的时候就听说有的大厂HR会让手撕红黑树。心中一直对这个数据结构保持着敬畏和向往，今天在将其撕出来后，用本篇博客加以记录，望周知。

🔥红黑树的概念

红黑树，也是一种二叉搜索树，但再每个结点上增加一个存储位置表示结点的颜色，可以是RED（红）或BLACK（黑）。通过对任何一条根到叶子的路径上各个结点的着色方式的限制，红黑树确保没有一条路径会比其他路径长出两倍，因而是接近平衡的。

一颗红黑树，是具有如下性质的二叉搜索树：

1. 每个结点不是红色就是黑色
2. 根结点是黑色的
3. 如果一个结点是红色，则它的两个孩子结点是黑色（即不会有连续的红结点）
4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点
5. 每个叶子结点都是黑色的（此处的叶子结点指的是空结点NIL）

其中，3和4是最重要的两点。

🔥手撕红黑树

红黑树结点的定义

红黑树的结点包含四个成员变量，模板类型T：可以存储K或者pair<K,V>类型，便于后期封装；三个指针：分别为指向左孩子结点的指针，指向右孩子结点的指针，指向父结点的指针；最后变量_col：枚举类型，可以存RED和BLACK。

enum Color
{RED,BLACK
};template<class T>
struct RBTreeNode
{RBTreeNode<T>(const T& t): _data(t), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}T _data;RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;Color _col;
};

红黑树主体需要实现的成员函数

// T: 可能是键值对<key,value>
//    可能是一个key
// 不论节点中存储的是<key, value> || key, 都是按照key来进行比较的
// KeyOfValue: 提取data中的Key
template<class K, class T, class KeyOfValue>
class RBTree
{typedef RBTreeNode<T> Node;
public:typedef RBTreeIterator<T, T&, T*> iterator;typedef RBTreeIterator<T, const T&, const T*> const_iterator;
public:RBTree() = default;RBTree(const RBTree<K, T, KeyOfValue>& t);// 插入值为data的节点// 返回值含义：iterator代表新插入节点   bool：代表释放插入成功std::pair<iterator, bool> Insert(const T& data);// Begin和End迭代器iterator Begin();iterator End();// 红黑树是否为空，是返回true，否则返回falsebool Empty()const;// 返回红黑树中有效节点的个数size_t Size()const;// 将红黑树中的有效节点删除void Clear();// 检测红黑树是否为有效的红黑树，注意：其内部主要依靠_IsValidRBTRee函数检测bool IsValidRBTRee()// 在红黑树中查找data，存在赶回该节点对应的迭代器，否则返回End()iterator Find(const T& data);~RBTree();
private:Node* _root;
};

红黑树的插入

红黑树是在二叉搜索树的基础上加上其平衡限制条件，因此红黑树的插入可分为两步：

1. 首先是按照二叉搜索树的方式插入结点
2. 检测插入结点后，红黑树的性质是否遭到破坏
   因为新结点的默认颜色是红色，因此：如果父结点的颜色是黑色，就没有违反性质，不需调整；担当插入结点的父节点也是红色时，就违反了性质3（不能有连在一起的红结点），此时需要对红黑树分情况讨论调整：

约定：cur为当前结点，p为父节点，g为祖父结点，u为叔叔结点。

• 情况一：cur为红，p为红，g为黑，u存在且为红

解决方式：将p，u变成黑色，g变成红色，然后把g改成cur，继续向上调整。

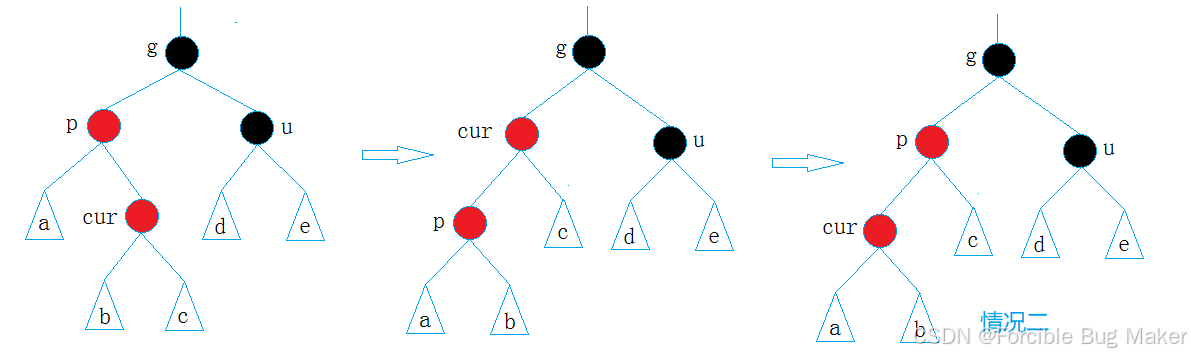
• 情况二：cur为红，p为红，g为黑，u不存在/u存在且为黑（这里需要做的其实就和AVL树中的单旋很像了，我们需要把u结点旋转下来，以维持平衡）

p为g的左孩子，cur为p的左孩子，进行右单旋；相反，p为g的右孩子，cur为p的右孩子，则进行左单旋。p变黑色，g变红色。

• 情况三（情况二的变体）：cur为红，p为红，g为黑，u不存在/u存在且为黑（其实就是双旋，除了不用调整平衡因子，其他的和AVL树的双旋并无差别）

p为g的左孩子，cur为p的右孩子，则针对p做左单旋转；相反，p为g的右孩子，cur为p的左孩子，则针对p做右单旋转。然后就转换成了情况2。

针对每种情况进行相应的处理即可：

// 插入值为data的节点
// 返回值含义：iterator代表新插入节点   bool：代表释放插入成功
std::pair<iterator, bool> Insert(const T& data)
{if (_root == nullptr) {_root = new Node(data);_root->_col = BLACK;return std::make_pair(iterator(_root, _root), true);}KeyOfValue kov;Node* parent = nullptr;Node* cur = _root;while (cur) {if (kov(cur->_data) < kov(data)) {parent = cur;cur = cur->_right;}else if (kov(cur->_data) > kov(data)) {parent = cur;cur = cur->_left;}else return std::make_pair(iterator(cur, _root), false);}cur = new Node(data);Node* InsertNode = cur;if (kov(parent->_data) < kov(data)) {parent->_right = cur;cur->_parent = parent;}else {parent->_left = cur;cur->_parent = parent;}while (parent && parent->_col == RED && cur->_col == RED) {Node* grandParent = parent->_parent;Node* uncle = nullptr;//   g// p   uif (grandParent->_left == parent) {uncle = grandParent->_right;if (uncle == nullptr || uncle->_col == BLACK) {if (parent->_left == cur) {RotateR(grandParent);parent->_col = BLACK;grandParent->_col = RED;}else {RotateL(parent);RotateR(grandParent);cur->_col = BLACK;grandParent->_col = RED;}break;}else {parent->_col = BLACK;grandParent->_col = RED;uncle->_col = BLACK;cur = grandParent;parent = grandParent->_parent;}}//   g// u   pelse {uncle = grandParent->_left;if (uncle == nullptr || uncle->_col == BLACK) {if (parent->_right == cur) {RotateL(grandParent);parent->_col = BLACK;grandParent->_col = RED;}else {RotateR(parent);RotateL(grandParent);cur->_col = BLACK;grandParent->_col = RED;}break;}else {parent->_col = BLACK;grandParent->_col = RED;uncle->_col = BLACK;cur = grandParent;parent = grandParent->_parent;}}}_root->_col = BLACK;return std::make_pair(iterator(InsertNode, _root), true);
}

在红黑树中，由于不用调节平衡因子，双旋的复杂度大大降低，直接使用单旋并在插入过程中调整结点颜色即可。
旋转的具体内容在AVL树中（【数据结构进阶】AVL树）讲解过，这里就不赘述了。

// 左单旋
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;Node* parentParent = parent->_parent;if (subRL)subRL->_parent = parent;subR->_left = parent;subR->_parent = parentParent;parent->_right = subRL;parent->_parent = subR;if (parentParent == nullptr) {_root = subR;}else {if (parentParent->_left == parent) {parentParent->_left = subR;}elseparentParent->_right = subR;}
}// 右单旋
void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;Node* parentParent = parent->_parent;if (subLR)subLR->_parent = parent;subL->_right = parent;subL->_parent = parentParent;parent->_left = subLR;parent->_parent = subL;if (parentParent == nullptr) {_root = subL;}else {if (parentParent->_left == parent) {parentParent->_left = subL;}elseparentParent->_right = subL;}
}

find

和二叉搜索树的查找规则相同。

// 在红黑树中查找data，存在赶回该节点对应的迭代器，否则返回End()
iterator Find(const T& data)
{KeyOfValue kov;Node* cur = _root;while (cur) {if (kov(cur->_data) < kov(data))cur = cur->_right;else if (kov(cur->_data) > kov(data))cur = cur->_left;else return iterator(cur, _root);}return iterator(nullptr, _root);
}

Empty和Size

Empty接口函数用来判断树是否为空；Size用来计算返回树结点的个数。

// 红黑树是否为空，是返回true，否则返回false
bool Empty()const
{return _root == nullptr;
}
// 返回红黑树中有效节点的个数
size_t Size()const
{return _Size(_root);
}size_t _Size(Node* root)
{return root == nullptr ? 0 : _Size(root->_left) + _Size(root->_right) + 1;
}

拷贝构造

RBTree(const RBTree<K, T, KeyOfValue>& t)
{_root = _Copy(t._root);
}Node* _Copy(Node* root)
{if (root == nullptr)return nullptr;Node* newRoot = new Node(root->_data);newRoot->_left = _Copy(root->_left);newRoot->_right = _Copy(root->_right);return newRoot;
}

析构函数和clear

// 将红黑树中的有效节点删除
void Clear()
{_Destroy(_root);_root = nullptr;
}~RBTree()
{_Destroy(_root);_root = nullptr;
}void _Destroy(Node* root)
{if (root == nullptr)return;_Destroy(root->_left);_Destroy(root->_right);delete root;
}

检测是否为合法红黑树

在IsValidRBTRee中，首先算出一条路径上的黑结点个数digit_black，然后在每条路径递归到空结点时判断黑结点个数是否相等，即可验证性质4（所有路径上黑结点个数相等）；递归的过程中，判断当前结点和父节点的颜色是否同时为红，即可验证性质3（没有连续的红结点）

// 检测红黑树是否为有效的红黑树，注意：其内部主要依靠_IsValidRBTRee函数检测
bool IsValidRBTRee()
{if (_root == nullptr)return true;Node* cur = _root;size_t digit_black = 0;while (cur) {if (cur->_col == BLACK)++digit_black;cur = cur->_left;}return _IsValidRBTRee(_root, digit_black, 0);
}bool _IsValidRBTRee(Node* pRoot, size_t blackCount, size_t pathBlack)
{if (pRoot == nullptr) {if (blackCount == pathBlack)return true;else return false;}if (pRoot->_col == RED && pRoot->_parent->_col == RED) {return false;}if (pRoot->_col == BLACK) {return _IsValidRBTRee(pRoot->_left, blackCount, pathBlack + 1)&& _IsValidRBTRee(pRoot->_right, blackCount, pathBlack + 1);}else {return _IsValidRBTRee(pRoot->_left, blackCount, pathBlack)&& _IsValidRBTRee(pRoot->_right, blackCount, pathBlack);}
}

Begin和End

这两个函数用于获取红黑树的头对象和尾迭代器。

// Begin和End迭代器
iterator Begin() 
{return iterator(_LeftMost(), _root);
}
iterator End()
{return iterator(nullptr, _root);
}// 获取红黑树最左侧节点
Node* _LeftMost()
{if (_root == nullptr)return nullptr;Node* parent = _root;Node* cur = parent->_left;while (cur) {parent = cur;cur = cur->_left;}return parent;
}

红黑树的迭代器接口

迭代器的好处是可以方便遍历，使数据结构的底层实现变的透明，从而降低代码编写的复杂程度。

template<class T, class Ref, class Ptr>
struct RBTreeIterator
{typedef RBTreeNode<T> Node;typedef RBTreeIterator<T, Ref, Ptr> Self;RBTreeIterator(Node* pNode,Node* root): _pNode(pNode),_root(root){}// 让迭代器具有类似指针的行为Ref operator*();Ptr operator->();// 然迭代器可以移动：前置/后置++  Self& operator++();Self operator++(int);// 然迭代器可以移动：前置/后置-- Self& operator--();Self operator--(int);// 让迭代器可以比较bool operator!=(const Self& s)const;bool operator==(const Self& s)const;private:Node* _pNode;Node* _root;
};

* 解引用和 -> 访问

// 让迭代器具有类似指针的行为
Ref operator*()
{return _pNode->_data;
}
Ptr operator->()
{return &(_pNode->_data);
}

operator++()

二叉树的中序遍历并不难实现，但是要实现从任意一个结点按中序遍历跑到下一个结点，这就有相当难度了。
具体逻辑为：

1. 右子树不为空，访问右子树的最左结点。
2. 右子树为空（代表当前结点所在子树访问完了），沿着到根节点的路线，孩子是父亲左的那个祖先结点，就是下一个要访问的结点。

// 迭代器可以移动：前置/后置++  
Self& operator++()
{if (_pNode->_right) {_pNode = _pNode->_right;while (_pNode->_left) _pNode = _pNode->_left;}else {Node* cur = _pNode;Node* parent = cur->_parent;while (parent && cur == parent->_right) {cur = parent;parent = parent->_parent;}_pNode = parent;}return *this;
}Self operator++(int)
{Node* rem = _pNode;if (_pNode->_right) {_pNode = _pNode->_right;while (_pNode->_left)_pNode = _pNode->_left;}else {Node* cur = _pNode;Node* parent = cur->_parent;while (parent && cur == parent->_right) {cur = parent;parent = parent->_parent;}_pNode = parent;}return Self(rem);
}

operator- - ()

这时候要判断当前迭代器是否指向尾End()，同时判断树是否为空，这就要用到传入迭代器对象中的_root了。在找到End()的前一个结点之后，按照和operator++()相反的逻辑即可实现operator--()。
具体逻辑为：

1. 左子树不为空，访问左子树的最右结点。
2. 左子树为空（代表当前结点所在子树访问完了），沿着到根结点的路线，孩子是父亲右的那个祖先结点，就是下一个要访问的结点。

// 迭代器可以移动：前置/后置-- 
Self& operator--()
{if (_pNode == nullptr) {if (_root == nullptr)assert(false);Node* parent = _root;Node* cur = parent->_right;while (cur) {parent = cur;cur = cur->_right;}_pNode = parent;return *this;}if (_pNode->_left) {_pNode = _pNode->_left;while (_pNode->_right)_pNode = _pNode->_right;}else {Node* cur = _pNode;Node* parent = cur->_parent;while (parent && cur == parent->_left) {cur = parent;parent->_parent;}_pNode = parent;}return *this;
}Self operator--(int)
{if (_pNode == nullptr) {if (_root == nullptr)assert(false);Node* parent = _root;Node* cur = parent->_right;while (cur) {parent = cur;cur = cur->_right;}_pNode = parent;return Self(nullptr);}Node* rem = _pNode;if (_pNode->_left) {_pNode = _pNode->_left;while (_pNode->_right)_pNode = _pNode->_right;}else {Node* cur = _pNode;Node* parent = cur->_parent;while (parent && cur == parent->_left) {cur = parent;parent->_parent;}_pNode = parent;}return Self(rem);
}

迭代器比较相等

底层就是用指针作比较。

// 让迭代器可以比较
bool operator!=(const Self& s)const
{return _pNode != s._pNode;
}bool operator==(const Self& s)const
{return _pNode == s._pNode;
}

🌈结语

红黑树和AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是O($lo{g}_{2}N$)，红黑树不追求绝对平衡，其只需保证最长路径不超过最短路径的2倍，相对而言，降低了插入和旋转的次数，所以在经常进行增删的结构中性能比AVL树更优，而且红黑树实现比较简单，所以实际运用中红黑树更多。
红黑树的底层实现到这里就要结束了，本篇的数据结构较为复杂，模板的使用也有很多容易出错的点，需要多加体会。感谢大家的支持♥