CSS平面转换-平移
平面转换-平移
属性 transform: translate(X轴移动距离, Y轴移动距离);
取值
- 像素单位取值
- 百分比(参照盒子自身尺寸计算结果)
- 正负均可
技巧 - translate()只写一个值表示只沿着X轴移动
- 单独设置X或Y轴距离:translateX()或translateY()
代码
<!DOCTYPE html>
<html lang="en">
<head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scale=1.0"><title>平面转换-平移</title><style>.father {width: 500px;height: 300px;margin: 100px auto;border: 1px solid #000000;}.son {width: 200px;height: 100px;background-color: pink;transition: all 0.5s;}.father:hover .son {transform: translate(100px, 200px);/* 百分比参照盒子自身尺寸 *//* transform: translate(50%,100%); *//* transform: translate(-50%,100%); *//* transform: translateX(100px); */transform: translateY(200px);}</style>
</head>
<body><div class="father"><div class="son"></div></div></body>
</html>
相关文章:

CSS平面转换-平移
平面转换-平移 属性 transform: translate(X轴移动距离, Y轴移动距离); 取值 像素单位取值百分比(参照盒子自身尺寸计算结果)正负均可 技巧translate()只写一个值表示只沿着X轴移动单独设置X或Y轴距离:translateX()或translateY() 代码 …...

Linux-3:Shell编程——基础语法(0-50%)
目录 前言 一、变量 1.定义变量 2.使用变量 3.修改变量 4.将命令的结果赋值给变量 5.只读变量 6.删除变量 二、传递参数 三、字符串 1.字符串举例 2.统计字符串长度 3.字符串拼接 4.截取字符串 总结 前言 Shell是一种程序设计语言。作为命令语言,它…...
)
C++ --> string类模拟实现(附源码)
欢迎来到我的Blog,点击关注哦💕 前言: C中STL扮演着极其重要的角色,学习C重中之重的就是学习STL,虽然string不作为containers的其中一员,但是也是值得学习的le类。下面就进行string的模拟实现 string的模拟…...

基于PHP+MySQL组合开发的微信活动投票小程序源码系统 带完整的安装代码包以及搭建部署教程
系统概述 在当今数字化时代,微信作为社交媒体的巨头,为企业和个人提供了丰富的互动营销平台。其中,投票活动作为一种有效的用户参与和互动方式,被广泛应用于各种场景。为了满足这一需求,我们推出了一款基于PHPMySQL组…...

利用Arcgis设置分式标注(分子分母标注)
因工作需要,需要设置分式标注,下面详细介绍下如何利用arcgis 设置分式标注,以下操作以供参考,如有疑义可提出。 一、准备工作 软件:arcmap 示例数据:行政区shp矢量图 二、操作步骤 1.添加数据 将行政区sh…...

大麦网抢票攻略:使用Python Selenium实现
随着互联网技术的发展,在线购票已成为人们获取演出、比赛等活动门票的主要方式。然而,面对热门活动,门票往往在开售瞬间被抢购一空。为了解决这一问题,本文将介绍如何利用Python和Selenium技术实现大麦网的自动抢票。 1. 环境准备…...

Navicat 在整个数据库中查找字符
Navicat 在整个数据库中查找字符 1.首先打开Navicat,连接目标数据库。2.选择工具选项卡,选择在数据库或模式中查找。3.查找前填入关键字信息,点击查找4.双击查找到数据,进行查看 说明:当我们知道数据库有数据的关键字,…...

Python基础—处理时间问题
一文帮助您解决99%时间处理问题...

如何选择合适的自动化测试工具!
选择合适的自动化测试工具是一个涉及多方面因素的决策过程。以下是一些关键步骤和考虑因素,帮助您做出明智的选择: 一、明确测试需求和目标 测试范围:确定需要自动化的测试类型(如单元测试、集成测试、UI测试等)和测试…...

数字图像边缘曲率计算及特殊点检测
一、曲率和数字图像边缘曲率检测常用方法简介 边缘曲率作为图像边缘特征的重要参数,不仅反映了边缘的几何形状信息,还对于图像识别、图像分割、目标跟踪等任务具有显著影响。 曲线的曲率(curvature)就是针对曲线上某个点的切线方向…...

python map
在 Python 中,如果你指的是字典(dictionary),可以使用字典的 .items() 方法来遍历键值对。Python 中没有严格意义上的 Map 类型,而是使用字典来实现类似于键值对映射的功能。 遍历字典的键值对 可以使用 for 循环和 …...

每日一练 - NFV部署应用环境
01 真题题目 NFV 常常部署在下列哪些应用环境中?(多选) A.数据中心 B.网络节点 C.用户接入侧 D.客户机/服务器 02 真题答案 ABC 03 答案解析 NFV(Network Functions Virtualization,网络功能虚拟化)是一种技术,它允许在标准的…...

031-GeoGebra中级篇-GeoGebra的布尔值
在 GeoGebra 中,布尔值和条件判断是实现动态数学模型和交互式几何图形的重要工具。布尔值,即逻辑值,只有两个可能的取值:真(True)或假(False)。通过使用布尔值,我们可以创…...

基于Debian用户安装星火商店
星火商店下载地址:https://www.spark-app.store/ 本文章我以kali linux来做示范 注:基本debian的linux包括ubuntu,mint linux,kali linux,Pop!_OS,deepin等等 1.点击下载最新版本 2.点击下载 3.点击开始下载(它会自动跳转网页) 4.选择要下载…...
课后习题答案)
《计算机网络》(第8版)课后习题答案
【1-01】 计算机网络可以向用户提供哪些服务? 解答:这道题没有现成的标准答案,因为可以从不同的角度来看“服务”。 首先要明确的是,计算机网络可以向用户提供的最重要的功能有两个:连通性和共享。所 谓连通性,就是计算机网络使上网用户之间都可以交换信息,好像这些用户…...
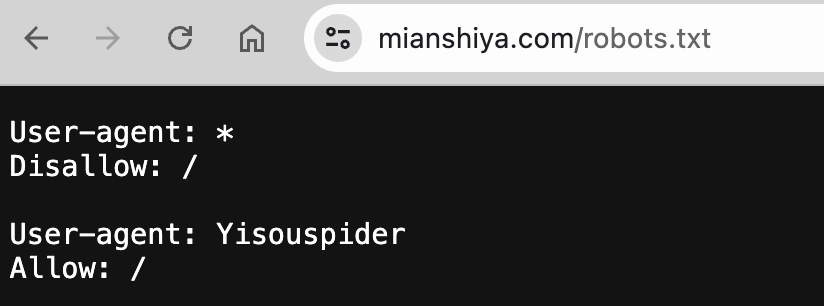
我们的网站被狗爬了!
大家好,我是程序员鱼皮。 世风日下,人心不古。我们的程序员面试刷题网站 《面试鸭》 才刚刚上线了一个多月,就由于过于火爆,被不少同行和小人发起网络攻击。 而且因为我们已经有 4500 多道人工整理的企业高频面试题、100 多个各…...

docker安装与container基本使用
安装 Homebrew 的 Cask 已经支持 Docker for Mac, mac用户狂喜 brew install --cask --appdir/Applications docker其他入门用法可参考 Docker Hello World- 菜鸟教程 或网上自行搜索博客学习。本文主要记录我运行go-zero-mall用到的一些注意点。当然,gonivinck项…...

掌握文本搜索的利器:深入解析 Linux grep 命令的强大功能
grep 是一个强大的命令行工具,用于在文件中搜索指定的模式(字符串或正则表达式)。它的名字来源于 "global regular expression print",常用于文本处理、日志分析等任务。以下是 grep 命令的详细介绍和常用操作: 基本用法 搜索匹配的行 grep "pattern"…...

【天机学堂】面试总结
写在前面,首先要将天机学堂包装一下,智慧教育平台》,暂时就想到这个。天机学堂文档 1.包装简历 待更新。。。...

Java中Stream操作
Java中Stream操作 Stream 和 Optional区别 用途不同:Stream 用于处理集合中的元素序列,支持丰富的中间操作和终端操作;Optional 用于表示一个值可能为 null 的情况,提供了一种更优雅的处理方式。数据处理 vs. 容器:S…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
