如何理解复信号z的傅里叶变换在频率v＜0的时候恒为0,是解析信号
考虑例子2.12.1的说法。
首先我尝试解释第二个说法。需要注意一个事实是
实函数f的傅里叶变换F的实部是偶函数，虚部是奇函数。如图所示：
注意的是这个图中虽然是离散傅里叶变换的性质，但是对于一般的傅里叶变换的性质是适用的。
推导过程如下：
若复信号的傅里叶变换在f＜0恒为零，则复信号是解析信号如何理解？
什么样的复函数f+ig进行傅里叶变换能使得f＜0的部分的函数值为实数，并且=0？
换个说法，固定f，寻找g，使得以上的结论成立，当g=f的希尔伯特变换f^时候成立，还有其他的函数h成立吗？
于是我就写过程如下，发现g完全由f决定，所以g是唯一的。
==========================================================================
相关文章：
如何理解复信号z的傅里叶变换在频率v＜0的时候恒为0,是解析信号
考虑例子2.12.1的说法。 首先我尝试解释第二个说法。需要注意一个事实是 实函数f的傅里叶变换F的实部是偶函数，虚部是奇函数。如图所示： 注意的是这个图中虽然是离散傅里叶变换的性质，但是对于一般的傅里叶变换的性质是适用的。 推导过程如下…...
大型赛事5G室内无线网络保障方案
大型活动往往才是国家综合实力的重要体现，其无线网络通信保障工作需融合各类新兴的5G业务应用，是一项技术难度高、方案复杂度高的系统工程。尤其在活动人员复杂、现场突发情况多、网络不稳定等情况下，如何形成一套高效、稳定的应急通信解决方…...
windows 2012域服务SYSVOL复制异常
这边文章是我多年前在BBS提问的，后来有高手回答，我把他保存了下来，最近服务器出现问题，终于有翻出来了！发出来希望能帮到更多人。 问题 我的环境，windows 2012。最近改了一些域策略，发现没有正…...
动态规划，蒙特卡洛，TD,Qlearing,Sars,DQN,REINFORCE算法对比
动态规划（Dynamic Programming, DP）通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。 动态规划的步骤 识别子问题：定义问题的递归解法，识别状态和选择。确定DP数组：确定存储子问题解的数据结构ÿ…...
HarmonyOS开发商城商品详情页
目录 一：功能概述 二：代码实现 三：效果图 一：功能概述 这一节，我们实现商品详情页的开发，具体流程就是在首页的商品列表点击商品跳转到商品详情页面，同时传递参数到该页面，通过参数调用商品详情接口在详情页展示商品的的详情信息。这里我们为了方便返回首页，在最顶…...
OS_操作系统的运行环境
2024.06.11:操作系统的运行环境学习笔记 第3节 操作系统的运行环境 3.1 操作系统引导3.2 操作系统内核3.2.1 内核资源管理3.2.2 内核基本功能 3.3 CPU的双重工作模式3.3.1 CPU处于用户态（目态）3.3.2 CPU处于内核态（管态） 3.4 特权…...
Maven下载和安装（详细版）
前言 Maven 的含义 Maven 是一个 java 项目管理 和构建工具，他可以定义项目结构，项目依托，并使用统一的方式进行自动化构建，是 java项目不可或缺的工具。 Maven 的 优点 1 提供 标准化的项目结构（具体规定了文件的…...
【优秀python大屏案例】基于python flask的前程无忧大数据岗位分析可视化大屏设计与实现
随着大数据和人工智能技术的迅猛发展，数据分析和可视化在各个行业中的应用越来越广泛。特别是在招聘领域，大数据分析不仅能够帮助企业更好地了解市场需求，还能为求职者提供科学的职业规划建议。本文探讨了基于Python Flask框架的前程无忧大数…...
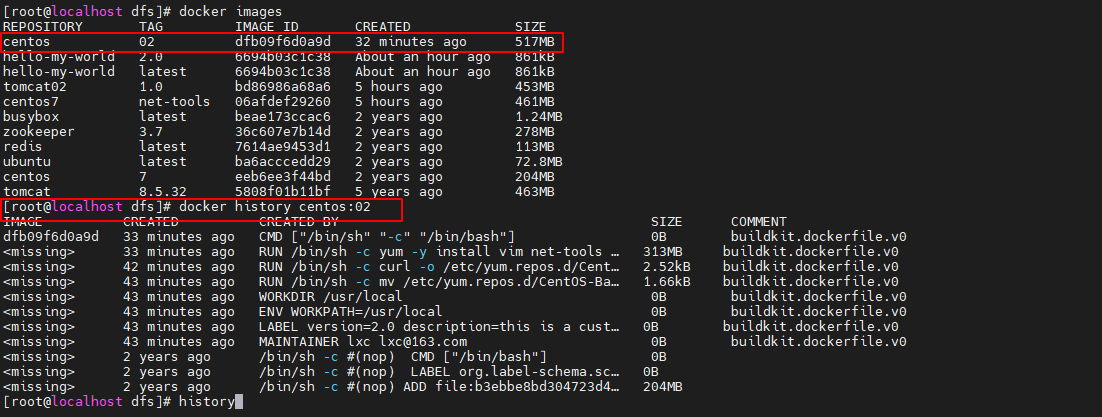
简单的docker学习 第3章docker镜像
第3章 Docker 镜像 3.1镜像基础 3.1.1 镜像简介 镜像是一种轻量级、可执行的独立软件包，也可以说是一个精简的操作系统。镜像中包含应用软件及应用软件的运行环境。具体来说镜像包含运行某个软件所需的所有内容，包括代码、库、环境变量和配置文件等…...
jquery.ajax + antd.Upload.customRequest文件上传进度
前情提要：大文件分片上传，需要利用Upload的customRequest属性自定义上传方法。也就是无法通过给Upload的action属性赋值上传地址进行上传，所以Upload组件自带的上传进度条，也没法直接用了，需要在customRequest中加工一…...
一层5x1神经网络绘制训练100轮后权重变化的图像
要完成这个任务，我们可以使用Python中的PyTorch库来建立一个简单的神经网络，网络结构只有一个输入层和一个输出层，输入层有5个节点，输出层有1个节点。训练过程中，我们将记录权重的变化，并在训练100轮后绘制…...
Project #0 - C++ Primer
知识点 1.pragma once C和C中的一个非标准但广泛支持的预处理指令，用于使当前源文件在单次编译中只被包含一次。 #pragma once class F {}; // 不管被导入多少次，只处理他一次2.explicit C中的一个关键字，它用来修饰只有一个参数的类构造函…...
git提交commit信息规范，fix，feat
可以确保团体合作中，从你的提交记录可以识别出你的动作 feat：新功能（featuer）fix: 修补bugdocs： 文档（documentation）style：格式（修改样式，不影响代码运行的…...
服务器 Linux 的文件系统初探
好久没更新文章了，最近心血来潮，重新开始知识的累计，做出知识的沉淀~ 万事万物皆文件 文件系统：操作系统如何管理文件，内部定义了一些规则或者定义所以在 Linux 中所有的东西都是以文件的方式进行操作在 Linux 中&am…...
关于Unity转微信小程序的流程记录
1.准备工作 1.unity微信小程序转换工具，minigame插件，导入后工具栏出现“微信小游戏" 2.微信开发者工具稳定版 3.MP微信公众平台申请微信小游戏，获得游戏appid 4.unity转webgl开发平台，Player Setting->Other Setting…...
AI入门指南：什么是人工智能、机器学习、神经网络、深度学习？
文章目录 一、前言二、人工智能(AI)是什么？起源概念人工智能分类人工智能应用 三、机器学习是什么？概念机器学习常见算法机器学习分类机器学习与人工智能的关系 四、神经网络是什么？概念神经网络组成部分神经网络模型神经网络和机器学习的关系…...
网络安全中的IOC是指的什么？
网络安全中的IOC（Indicators of Compromise）指的是威胁指标，是网络安全领域中的一个重要概念。它指的是可以用来识别计算机系统、网络或应用程序中已经受到攻击或遭受威胁的特定特征。这些特征可以是恶意文件、恶意域名、已知攻击工具等&…...
掌握AJAX技术：从基础到实战
文章目录 **引言****1. 什么是AJAX？****2. AJAX的工作原理**AJAX 示例使用 Fetch API 实现 AJAX **3. 如何在项目中使用AJAX****4. 处理AJAX请求的常见问题****5. AJAX与JSON的结合****6. 使用AJAX框架和库****7. 实战：创建一个动态表单****8. AJAX中的事…...
Unity UGUI 实战学习笔记(6)
仅作学习，不做任何商业用途 不是源码，不是源码! 是我通过"照虎画猫"写的，可能有些小修改 不提供素材，所以应该不算是盗版资源，侵权删 因为注册和登录面板的逻辑与数据存储方面已经相对完善 服务器面板逻辑…...
iOS面试之属性关键字(二)：常见面试题
Q:ARC下，不显式指定任何属性关键字时，默认的关键字都有哪些？ 对应基本数据类型默认关键字是:atomic,readwrite,assign 对于普通的 Objective-C 对象:atomic,readwrite,strong Q：atomic 修饰的属性是怎么样保存线程安全的&#x…...
React Native 开发环境搭建（全平台详解）
React Native 开发环境搭建（全平台详解） 在开始使用 React Native 开发移动应用之前，正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南，涵盖 macOS 和 Windows 平台的配置步骤，如何在 Android 和 iOS…...
ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码： prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
C++.OpenGL （14/64）多光源（Multiple Lights）
多光源（Multiple Lights） 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用： 方法一：使用 Homebrew 安装 Git（推荐） 步骤如下：打开终端（Terminal.app） 1.安装 Homebrew…...
【C++进阶篇】智能指针
C内存管理终极指南：智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分，它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构： use strict;/…...
Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型（算法、数据分析、机器学习等）不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...
C# WPF 左右布局实现学习笔记(1)
开发流程视频： https://www.youtube.com/watch?vCkHyDYeImjY&ab_channelC%23DesignPro Git源码： GitHub - CSharpDesignPro/Page-Navigation-using-MVVM: WPF - Page Navigation using MVVM 1. 新建工程 新建WPF应用（.NET Framework) 2.…...