Python解题 - CSDN周赛第38期
又来拯救公主了。。。本期四道题还是都考过,而且后面两道问哥在以前写的题解里给出了详细的代码(当然是python版),直接复制粘贴就可以过了——尽管这样显得有失公允,考虑到以后还会出现重复的考题,所以现在问哥的题解基本不会给出完整的代码了。但是如果理解了思路,写出来应该不难。
第一题:代写匿名信
小Q想要匿名举报XX领导不务正业!小Q害怕别人认出他的字迹。他选择从报纸上剪裁下来英文字母组成自己的举报信。现在小Q找来了报纸,和自己的举报信的Txt,你能帮他确定一下是否能够完成匿名信吗?
输入描述:第一行输入报纸上的英文。 第二行输入小Q匿名信的内容。 (1<=len(str)<=10000)
输出描述:如果能完成输出”Yes”,否则输出”No”。(区分大小写,不考虑空格)
分析
其实小Q要做的,就是把报纸上的一个个字符“剪”出来,然后拼成一封“匿名信”。于是我们只要检查报纸上每个字符的个数,是否足够拼成要写的匿名信就可以了,比如如果要写的匿名信内容是 ddd,那报纸上至少要有3个d。
所以代码实现就很简单了,有很多种做法,比如先找出匿名信里每个字符的个数,然后去报纸里找,是否有这个字符、数量是否足够,还可以先把报纸里的字符及个数统计出来,然后与匿名信的相应字符比较个数,如果少于匿名信,说明字符不够,反之就可以完成。
不过还要稍微判断一下,空格是不需要从报纸上剪下来的,所以不用分析空格的数量。
参考代码
from collections import Counter
a = Counter(magazine)
b = Counter(message)
for i in b:if i != " " and a[i] < b[i]:print("No")break
else:print("Yes")第二题:寻因找祖
寻找因子个数为n的最小整数x
分析
本题算是本期相对来说比较烧脑的一道了,虽然很久以前也考过。主要是数学上要对数字有一定的感觉。
首先我们知道,任意一个整数,都可以分解成若干个质数的乘积,而它的因子就是这些质因数的排列组合的乘积。比如整数 48 ,可以分解成 ,所以它的因子就有:
(所有整数的因子,也可以写成
或
)
(也可以写成
)
(也可以写成
)
(也可以写成
)
(也可以写成
)
(也可以写成
)
(也可以写成
)
(也可以写成
)
(也可以写成
)
(也可以写成
)
如果我们用公式来表示的话,就是任意一个整数都可以写成 的形式,其中
是质数,
。那么其因子个数
是什么关系呢?
我们先将问题简化来看,如果这个整数只有一个质因数,比如,,其因子中的 2 可以出现 0、1、2、3、4 次,也就是
,16 的因子个数
,等于因子 2 的出现次数,也就是 2 的幂 4 加一。
如果这个整数有两个质因数,根据排列组合原理,两个质因数的出现次数相乘,就是所有的排列组合个数,也就是因子个数。比如 ,其因子个数
。
所以回到我们 的表示方法,可以得到
。所以本题的问题就转化为在给定
的时候,找出
的大小,使得
最小。
要使该整数最小,我们首先要使作为底的 这些质因数比较小,所以,较小的质因数在这个最小的整数中至少会出现一次,也就是说
。(这应该比较好理解,在给定
的时候,如果可以求得
,那么以最小的质因数作为底,得到的结果必然最小。)
所以问哥使用的算法是,从 2(最小的质数)开始试, 必然是满足因子个数为
这个要求的,但却不一定是最小的整数。接着再用比 2 大的下一个质数 3 接着试,组成
的形式,其中
(其实就是将
进行因式分解),然后再换下个质数(2 和 3 必须出现一次)不断递归。因为
的因式分解组合是有限的,最终会递归到
的情况。所以把得到的所有数乘起来,就得到所有因子个数为
的整数,再从中找到最小的就是答案。
参考代码(部分)
def dfs(n, x = 2):if n == 1: return 1y = x + 1while not prime(y): # 查找下个质数y += 1 res = INFfor i in range(n, 1, -1):if n % i == 0:res = min(res, x**(i-1) * dfs(n//i, y))return res第三题:小Q新式棋盘
已知棋盘大小为n*n。 每个位置都有自己的权值q。该棋盘中有多少对行权值和小于列权值和。
分析
14期考过,以前的题解也给出了比较详细的代码及优化方案。其实也没什么可详细说的,就是按照字面意思分别比较行、列的和即可。
第四题:拯救公主
在Flower Kingdom里,住着一位美丽的公主Ana,有一天Ana得了一种怪病,神医告知国王,在遥远的幽谷中有一种药能治愈Ana, 但是神医只有一份不完整的地图,地图的描述如下: 该地图的共有3行,第一行有m列,m为奇数,第二行有m+1列,第三行有m+2列;每一行用一个字符串表示,只有【两种字符】;‘.'表示草地,可以从它上面通过,‘*’表示岩石,每一行最多一个‘*’; 入口在左上角,由于在对角线方向上,因此即使对角线两边都有岩石,但是缝隙较大,人可以通过,故人可以向八个方向行走; 真实地图是由该地图的【每一行无限循环】得到的,这种神奇的药草就生长在第x行第y列的草地上,药草可能会在岩石上;国王决定派遣勇敢的骑士David前去寻找拯救公主的解药;现在聪明的你是否知道David能否找到该药?
分析
17期考过,问哥还写了一篇比较详细的题解,其中给出了详细的代码,题目本身也不难,直接复制粘贴就可以过了。
相关文章:
Python解题 - CSDN周赛第38期
又来拯救公主了。。。本期四道题还是都考过,而且后面两道问哥在以前写的题解里给出了详细的代码(当然是python版),直接复制粘贴就可以过了——尽管这样显得有失公允,考虑到以后还会出现重复的考题,所以现在…...
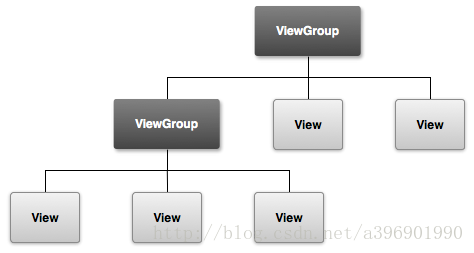
Android绘制——自定义view之onLayout
简介 在自定义view的时候,其实很简单,只需要知道3步骤: 测量——onMeasure():决定View的大小,关于此请阅读《Android自定义控件之onMeasure》布局——onLayout():决定View在ViewGroup中的位置绘制——onD…...

用Qt画一个温度计
示例1 以下是用Qt绘制一个简单的温度计的示例代码: #include <QPainter> #include <QWidget> #include <QApplication> class Thermometer : public QWidget { public:Thermometer(QWidget *parent 0); protected:void paintEvent(QPaintEvent …...
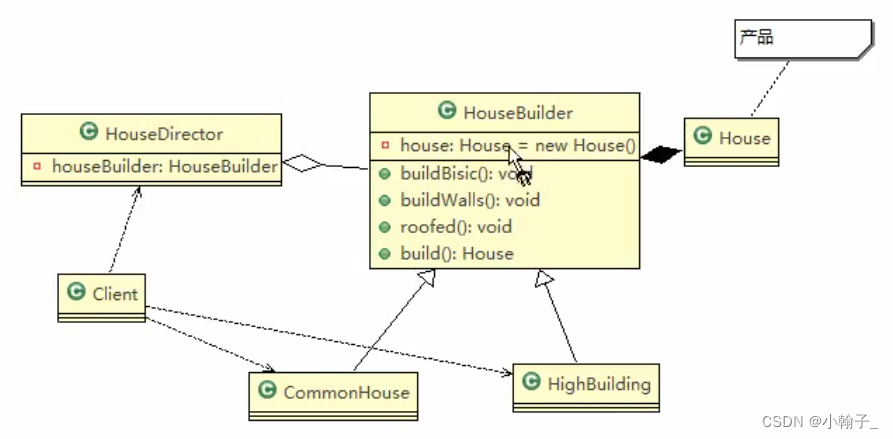
Java设计模式 04-建造者模式
建造者模式 一、 盖房项目需求 1)需要建房子:这一过程为打桩、砌墙、封顶 2)房子有各种各样的,比如普通房,高楼,别墅,各种房子的过程虽然一样,但是要求不要相同的. 3)请编写程序,完成需求. …...

安语未公告于2023年3月20日发布
因一些特殊原因,凡事都是有开始,高潮和结束三大过程,做出以下决定: 所有对 安语未文章 为之热爱、鞭策、奉献,和支持过的开发者: 注:所有资源以及资料都会正常下载和查看 如需联系࿱…...

进销存是什么?如何选择进销存系统?
什么是进销存?进销存软件概念起源于上世纪80年代,由于电算化的普及,计算机管理的推广,不少企业对于仓库货品的进货,存货,出货管理,有了强烈的需求,进销存软件的发展从此开始。 进入…...

基于BP神经网络的图像跟踪,基于BP神经网络的细胞追踪识别
目录 摘要 BP神经网络的原理 BP神经网络的定义 BP神经网络的基本结构 BP神经网络的神经元 BP神经网络激活函数及公式 基于BP神经网络的细胞识别追踪 matab编程代码 效果 结果分析 展望 摘要 智能驾驶,智能出行是现代社会发展的趋势之一,其中,客量预测对智能出行至关重要,…...
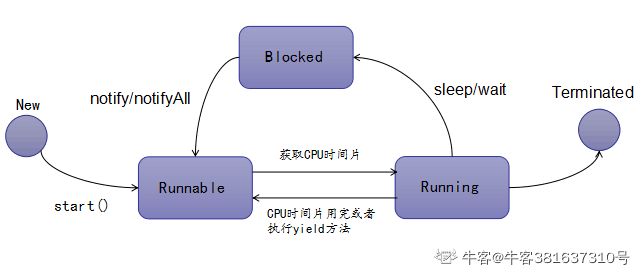
Java面试总结篇
引用介绍 1.线程安全不安全的概念 线程安全: 指多个线程在执行同一段代码的时候采用加锁机制,使每次的执行结果和单线程执行的结果都是一样的,不存在执行程序时出现意外结果。 线程不安全: 是指不提供加锁机制保护,有可能出现多个线程先后更改数据造成所得到的数据是脏…...
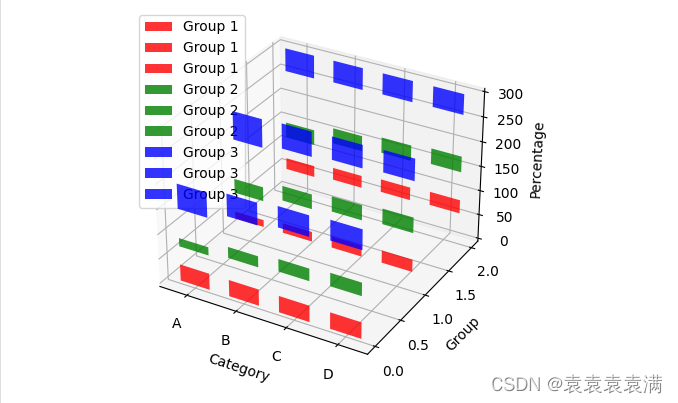
100天精通Python(可视化篇)——第80天:matplotlib绘制不同种类炫酷柱状图代码实战(簇状、堆积、横向、百分比、3D柱状图)
文章目录0. 专栏导读1. 普通柱状图2. 簇状柱形图3. 堆积柱形图4. 横向柱状图5. 横向双向柱状图6. 百分比堆积柱形图7. 3D柱形图8. 3D堆积柱形图9. 3D百分比堆积柱形图0. 专栏导读 🏆🏆作者介绍:Python领域优质创作者、CSDN/华为云/阿里云/掘金…...

【Java】UDP网络编程
文章目录前言DatagramSocketDatagramPacket注意事项与区别代码演示前言 UDP(user datagram protocol)的中文叫用户数据报协议,属于传输层。 UDP是面向非连接的协议,它不与对方建立连接,而是直接把我要发的数据报发给对…...
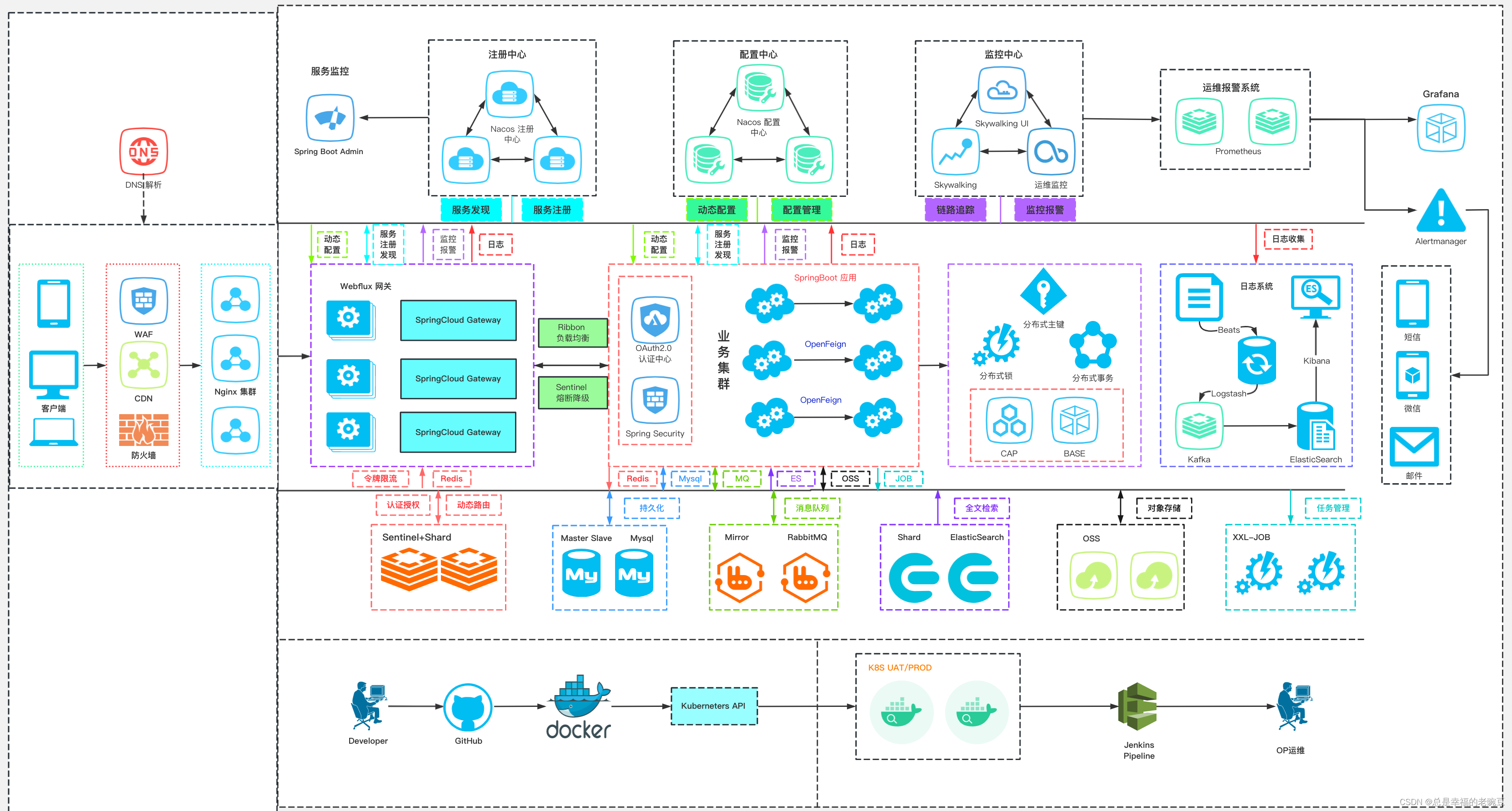
Springboot源代码总结
前言 编写微服务,巩固知识 文章目录 前言springboot原理springboot启动流程SpringBoot自动配置底层源码解析自动配置到底配了什么?自动配置类条件注解Starter机制@ConditionalOnMissingBeanSpringBoot启动过程源码解析构造SpringApplication对象SpringBoot完整的配置优先级s…...
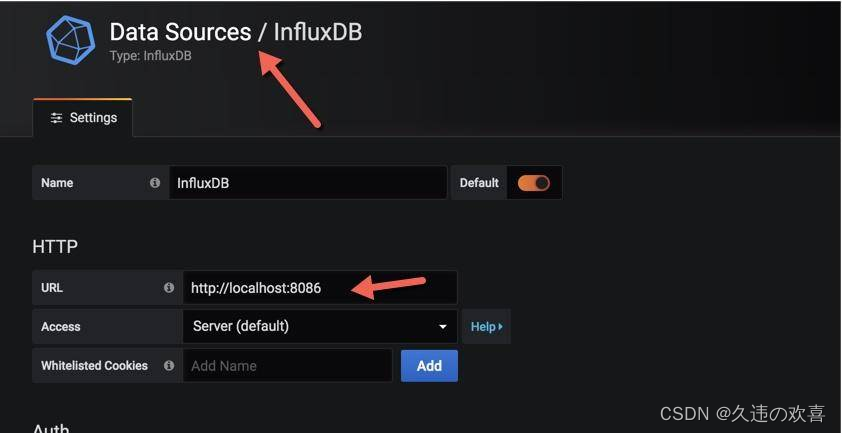
JVM监控搭建
文章目录JVM监控搭建整体架构JolokiaTelegrafInfluxdbGrafanaJVM监控搭建 整体架构 JVM 的各种内存信息,会通过 JMX 接口进行暴露。 Jolokia 组件负责把 JMX 信息翻译成容易读取的 HTTP 请求。Telegraf 组件作为一个通用的监控 agent,和 JVM 进程部署在…...

java中如何优化大量的if...else...
目录 策略模式(Strategy Pattern) 工厂模式(Factory Pattern) 映射表(Map) 数据驱动设计(Data-Driven Design) 策略模式(Strategy Pattern) 将每个条件分…...
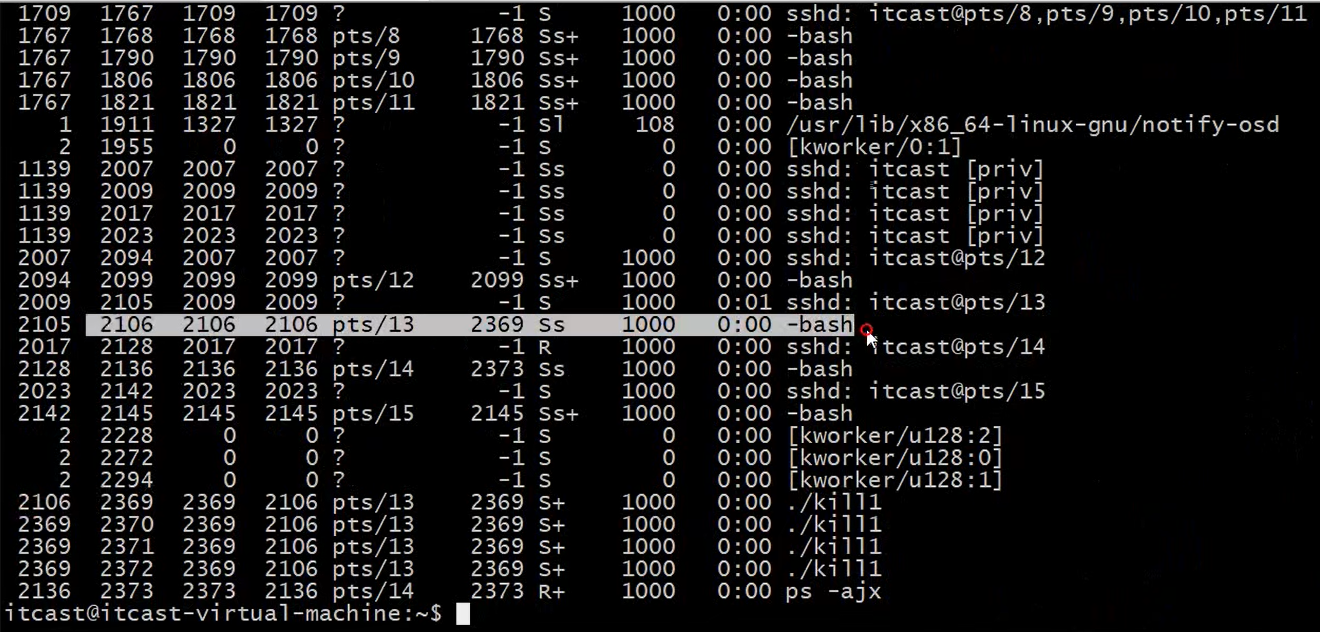
24. linux系统基础
两个进程间想通讯,必须要通过内核,今天讲的信号其实本质也是讲进程间通讯的意思,那么你为什么可以在shell环境下,可以和一个进程发kill-9啊? shell是不是相当于一个进程?你自己运行的那个进程是不是也相当于…...

【C++】面试101,二叉搜索树的最近公共祖先,在二叉树中找到两个节点的最近公共祖先,序列化二叉树,重建二叉树,输出二叉树的右视图,组队竞赛,删除公共字符
目录 1.二叉搜索树的最近公共祖先 2.在二叉树中找到两个节点的最近公共祖先 3.序列化二叉树 4.重建二叉树 5.输出二叉树的右视图 6.组队竞赛 7.删除公共字符 1.二叉搜索树的最近公共祖先 这是一个简单的问题,因为是二叉搜索树(有序)&am…...

Java常见面试题及解答
Java常见面试题及解答1 面向对象的三个特征2 this,super关键字3 基础数据类型4 public、protected、default、private5 接口6 抽象类6.1 抽象类和接口的区别7 重载(overload)、重写(override)8 final、finalize、final…...
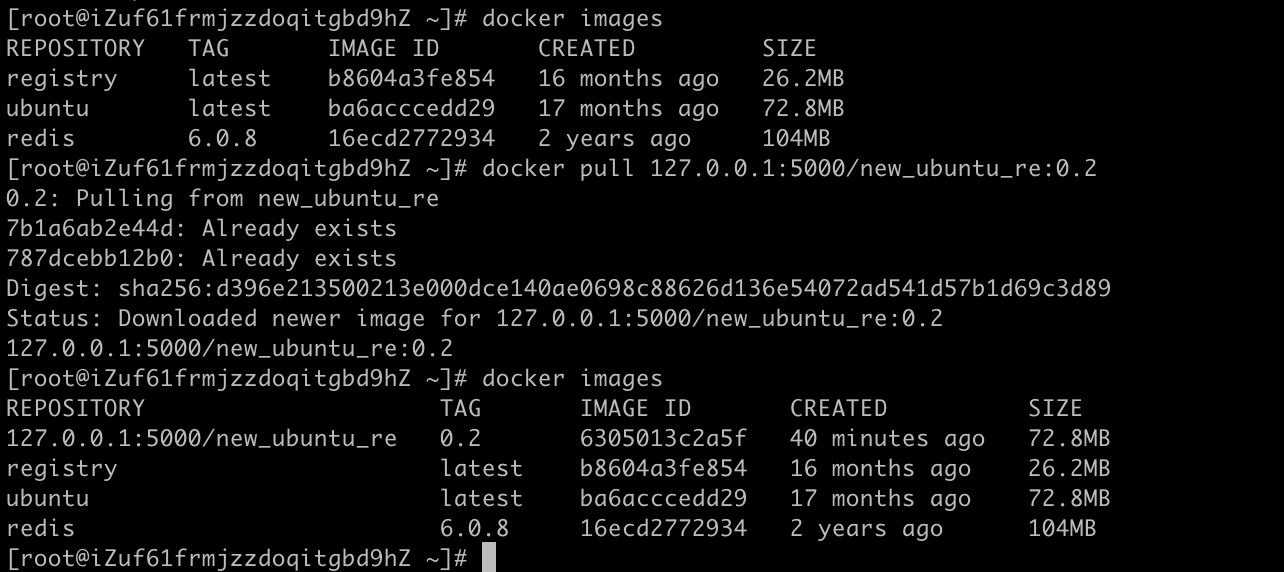
【Docker】镜像的原理定制化镜像
文章目录镜像是什么UnionFS(联合文件系统)Docker镜像加载原理制作本地镜像 docker commit -m"提交的描述信息" -a"作者" 容器ID 要创建的目标镜像名:[标签名]案例演示ubuntu安装vim本地镜像发布到阿里云本地镜像发布到阿里云流程将本…...

国内版的ChatGPT弯道超车的机会在哪里?
前言 从去年11月最后一天ChatGPT诞生,截至目前,ChatGPT的热度可谓是爆了。众所周知,ChatGPT是美国“开放人工智能研究中心”研发的聊天机器人程序,它是一个人工智能技术驱动的自然语言处理工具,它能够通过学习和理解人…...

【字符串】
string1.char str[]类型fgets(s,10000,stdin) cin.getline(cin,10000) strlen(str)sizeof 求静态数组长度2.string类型getline(cin,a) cin.getline(cin,10000) str.lenth()str.size()cin 遇到空格就停止3.gets 函数char str[20];gets(str);4.puts 函数puts(str) 相当于 cout<…...

加载驱动之后无法在/dev/下生成vedio0
前言 环境介绍: 1.编译环境 Ubuntu 18.04.5 LTS 2.SDK orangepi Linux 5.4 SDK 3.uboot v2020.04 4.gcc gcc-linaro-7.5.0-2019.12-x86_64_arm-linux-gnueabihf 5.单板 orangepi pc plus 一、问题 继上一篇成功加载gc2035.ko文件之后,理论上…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
